Skip to main content
Global

6.5: Fricção (Parte 2)

  1. Last updated
  2. Save as PDF
  • Page ID
    185449

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Fricção e o plano inclinado

    Uma situação em que o atrito desempenha um papel óbvio é a de um objeto em um declive. Pode ser uma caixa sendo empurrada por uma rampa até uma doca de carga ou um skatista descendo uma montanha, mas a física básica é a mesma. Normalmente generalizamos a superfície inclinada e a chamamos de plano inclinado, mas depois fingimos que a superfície é plana. Vejamos um exemplo de análise de movimento em um plano inclinado com atrito.

    Exemplo\(\PageIndex{1}\): Downhill Skier

    Um esquiador com uma massa de 62 kg está deslizando por uma encosta nevada a uma velocidade constante. Encontre o coeficiente de atrito cinético para o esquiador se o atrito for conhecido como 45,0 N.

    Estratégia

    A magnitude do atrito cinético é dada como 45,0 N. O atrito cinético está relacionado à força normal N por f k =\(\mu_{k}\) N; assim, podemos encontrar o coeficiente de atrito cinético se pudermos encontrar a força normal no esquiador. A força normal é sempre perpendicular à superfície e, como não há movimento perpendicular à superfície, a força normal deve ser igual à componente do peso do esquiador perpendicular à inclinação. (Veja a Figura\(\PageIndex{1}\), que repete uma figura do capítulo sobre as leis do movimento de Newton.)

    A figura mostra um esquiador descendo uma ladeira que forma um ângulo de 25 graus com a horizontal. Um sistema de coordenadas x y é mostrado, inclinado de forma que a direção x positiva fique paralela à inclinação, apontando para cima da inclinação, e a direção y positiva esteja fora da inclinação, perpendicular a ela. O peso do esquiador, rotulado w, é representado por uma seta vermelha apontando verticalmente para baixo. Esse peso é dividido em dois componentes, w sub y é perpendicular à inclinação apontando na direção y negativa e w sub x é paralelo à inclinação, apontando na direção menos x. A força normal, chamada N, também é perpendicular à inclinação, igual em magnitude, mas apontando para fora, oposta em direção a w sub y. O atrito, f, é representado por uma seta vermelha apontando para cima. Além disso, a figura mostra um diagrama de corpo livre que mostra as magnitudes e direções relativas de f, N, w e os componentes w sub x e w sub y de w. Em ambos os diagramas, o vetor w é rabiscado à medida que é substituído por seus componentes.
    Figura\(\PageIndex{1}\): O movimento do esquiador e o atrito são paralelos à inclinação, por isso é mais conveniente projetar todas as forças em um sistema de coordenadas em que um eixo é paralelo à inclinação e o outro é perpendicular (eixos mostrados à esquerda do esquiador). A força normal\(\vec{N}\) é perpendicular à inclinação e o atrito\(\vec{f}\) é paralelo à inclinação, mas o peso do esquiador\(\vec{w}\) tem componentes ao longo dos dois eixos, ou seja,\(\vec{w}_{y}\)\(\vec{w}_{x}\) e. A força normal\(\vec{N}\) é igual em magnitude a\(\vec{w}_{y}\), portanto, não há movimento perpendicular à inclinação. No entanto,\(\vec{f}\) é menor do que\(\vec{w}_{x}\) em magnitude, então há aceleração descendo a inclinação (ao longo do eixo x).

    Nós temos

    \[N = w_{y} = w \cos 25^{o} = mg \cos 25^{o} \ldotp\]

    Substituindo isso em nossa expressão por atrito cinético, obtemos

    \[f_{k} = \mu_{k} mg \cos 25^{o},\]

    o que agora pode ser resolvido para o coeficiente de atrito cinético\(\mu_{k}\).

    Solução

    Resolvendo\(\mu_{k}\) doações

    \[\mu_{k} = \frac{f_{k}}{N} = \frac{f_{k}}{w \cos 25^{o}} = \frac{f_{k}}{mg \cos 25^{o}} \ldotp\]

    Substituindo valores conhecidos no lado direito da equação,

    \[\mu_{k} = \frac{45.0\; N}{(62\; kg)(9.80\; m/s^{2})(0.906)} = 0.082 \ldotp\]

    Significância

    Esse resultado é um pouco menor do que o coeficiente listado na Tabela 6.1 para madeira encerada na neve, mas ainda é razoável, pois os valores dos coeficientes de atrito podem variar muito. Em situações como essa, onde um objeto de massa m desliza por uma encosta que forma um ângulo\(\theta\) com a horizontal, o atrito é dado por f k =\(\mu_{k}\) mg cos\(\theta\). Todos os objetos deslizam por uma encosta com aceleração constante nessas circunstâncias.

    Discutimos que quando um objeto repousa sobre uma superfície horizontal, a força normal que o sustenta é igual em magnitude ao seu peso. Além disso, o atrito simples é sempre proporcional à força normal. Quando um objeto não está em uma superfície horizontal, como no plano inclinado, devemos encontrar a força atuando sobre o objeto que é direcionada perpendicularmente à superfície; é um componente do peso.

    Agora, derivamos uma relação útil para calcular o coeficiente de atrito em um plano inclinado. Observe que o resultado se aplica somente a situações em que o objeto desliza em velocidade constante pela rampa.

    Um objeto desliza por um plano inclinado a uma velocidade constante se a força total sobre o objeto for zero. Podemos usar esse fato para medir o coeficiente de atrito cinético entre dois objetos. Conforme mostrado no exemplo\(\PageIndex{1}\), o atrito cinético em uma inclinação é f k =\(\mu_{k}\) mg cos\(\theta\). O componente do peso abaixo da inclinação é igual a mg sin\(\theta\) (veja o diagrama de corpo livre na Figura\(\PageIndex{1}\)). Essas forças atuam em direções opostas, então quando elas têm a mesma magnitude, a aceleração é zero. Escrevendo isso,

    \[\mu_{k} mg \cos \theta = mg \sin \theta \ldotp\]

    Resolvendo\(\mu_{k}\), descobrimos que

    \[\mu_{k} = \frac{mg \sin \theta}{mg \cos \theta} = \tan \theta \ldotp\]

    Coloque uma moeda em um livro e incline-a até que a moeda deslize a uma velocidade constante pelo livro. Talvez seja necessário tocar levemente no livro para que a moeda se mova. Meça o ângulo de inclinação em relação à horizontal e encontre\(\mu_{k}\). Observe que a moeda não começa a deslizar até que um ângulo maior do que\(\theta\) seja alcançado, pois o coeficiente de atrito estático é maior que o coeficiente de atrito cinético. Pense em como isso pode afetar o valor\(\mu_{k}\) e sua incerteza.

    Explicações do atrito em escala atômica

    Os aspectos mais simples do atrito tratados até agora são suas características macroscópicas (em grande escala). Grandes avanços foram feitos na explicação em escala atômica do atrito durante as últimas décadas. Os pesquisadores estão descobrindo que a natureza atômica do atrito parece ter várias características fundamentais. Essas características não apenas explicam alguns dos aspectos mais simples do atrito, mas também têm o potencial para o desenvolvimento de ambientes quase livres de atrito que poderiam economizar centenas de bilhões de dólares em energia que atualmente está sendo convertida (desnecessariamente) em calor.

    \(\PageIndex{2}\)A figura ilustra uma característica macroscópica do atrito que é explicada pela pesquisa microscópica (em pequena escala). Observamos que o atrito é proporcional à força normal, mas não à quantidade de área em contato, uma noção um tanto contra-intuitiva. Quando duas superfícies rugosas estão em contato, a área de contato real é uma pequena fração da área total porque somente pontos altos se tocam. Quando uma força normal maior é exercida, a área de contato real aumenta e descobrimos que o atrito é proporcional a essa área.

    Esta figura tem duas partes, cada uma das quais mostra duas superfícies paralelas ásperas próximas uma da outra. Como as superfícies são irregulares, as duas superfícies entram em contato uma com a outra somente em determinados pontos, deixando espaços entre eles. Na primeira parte, a força normal é pequena, de modo que as superfícies estão mais afastadas e a área de contato entre as duas superfícies é muito menor do que a área total. Na segunda parte, a força normal é grande, de modo que as duas superfícies ficam muito próximas uma da outra e a área de contato entre as duas superfícies aumenta.
    Figura\(\PageIndex{2}\): Duas superfícies rugosas em contato têm uma área de contato real muito menor do que sua área total. Quando a força normal é maior como resultado de uma maior força aplicada, a área de contato real aumenta, assim como o atrito.

    No entanto, a visão em escala atômica promete explicar muito mais do que as características mais simples do atrito. O mecanismo de como o calor é gerado agora está sendo determinado. Em outras palavras, por que as superfícies ficam mais quentes quando esfregadas? Essencialmente, os átomos estão ligados uns aos outros para formar redes. Quando as superfícies se esfregam, os átomos da superfície aderem e fazem com que as redes atômicas vibrem, criando essencialmente ondas sonoras que penetram no material. As ondas sonoras diminuem com a distância e sua energia é convertida em calor. Reações químicas relacionadas ao desgaste por atrito também podem ocorrer entre átomos e moléculas nas superfícies. A figura\(\PageIndex{3}\) mostra como a ponta de uma sonda desenhada sobre outro material é deformada pelo atrito em escala atômica. A força necessária para arrastar a ponta pode ser medida e está relacionada à tensão de cisalhamento, que é discutida em Equilíbrio estático e elasticidade. A variação na tensão de cisalhamento é notável (mais do que um fator de 1012) e difícil de prever teoricamente, mas a tensão de cisalhamento está produzindo uma compreensão fundamental de um fenômeno de grande escala conhecido desde os tempos antigos: o atrito.

    Esta figura mostra um modelo molecular de uma sonda que é arrastada sobre a superfície de um substrato. O substrato é representado por uma grade retangular de pequenas esferas, cada esfera representando um átomo. A sonda, composta por uma grade diferente de pequenas esferas, tem a forma de uma pirâmide invertida com um pico achatado e camadas horizontais de átomos. A pirâmide está um pouco distorcida por causa do atrito. As interações atômicas e moleculares ocorrem na interface entre a sonda e o substrato. O atrito, f, é paralelo à superfície e na direção oposta ao movimento da sonda.
    Figura\(\PageIndex{3}\): A ponta de uma sonda é deformada lateralmente pela força de atrito à medida que a sonda é arrastada por uma superfície. As medições de como a força varia para diferentes materiais estão fornecendo informações fundamentais sobre a natureza atômica do atrito.
    Simulação

    Descreva um modelo de atrito em nível molecular. Descreva a matéria em termos de movimento molecular. A descrição deve incluir diagramas para apoiar a descrição; como a temperatura afeta a imagem; quais são as diferenças e semelhanças entre o movimento de partículas sólidas, líquidas e gasosas; e como o tamanho e a velocidade das moléculas de gás se relacionam com objetos do cotidiano.

    Exemplo\(\PageIndex{2}\): Sliding Blocks

    Os dois blocos da Figura\(\PageIndex{4}\) são presos um ao outro por uma corda sem massa que é enrolada em uma polia sem atrito. Quando o bloco inferior de 4,00 kg é puxado para a esquerda pela força constante\(\vec{P}\), o bloco superior de 2,00 kg desliza sobre ele para a direita. Encontre a magnitude da força necessária para mover os blocos em velocidade constante. Suponha que o coeficiente de atrito cinético entre todas as superfícies seja 0,400.

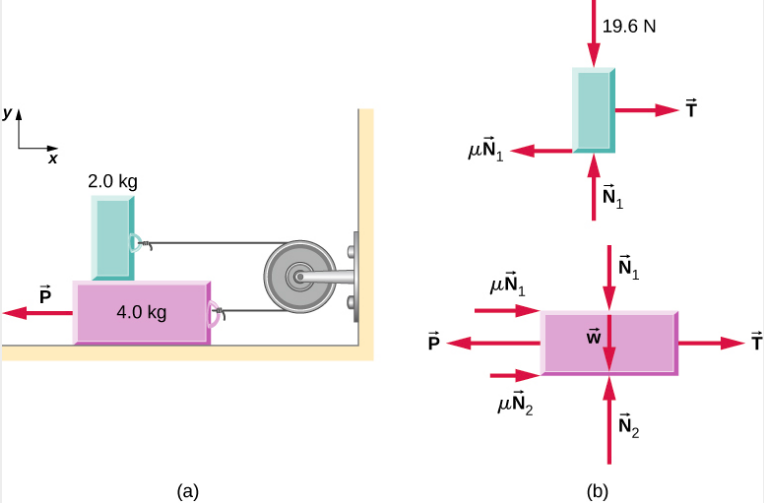
    A Figura (a) mostra uma ilustração de um bloco de 4,0 kg em uma superfície horizontal e um bloco de 2,0 kg apoiado em cima dele. Uma polia é conectada horizontalmente a uma parede à direita dos blocos. Os blocos são conectados por uma corda que passa de um bloco, sobre a polia e ao outro bloco, de forma que a corda fique na horizontal e à direita de cada bloco. Uma força P puxa o bloco inferior para a esquerda. Um sistema de coordenadas x y é mostrado, com x positivo à direita e y positivo para cima. A Figura (b) mostra os diagramas de corpo livre dos blocos. O bloco superior tem forças mu vezes vetor N sub 1 para a esquerda, vetor T para a direita, 19,6 N verticalmente para baixo e vetor N sub 1 para cima. O bloco inferior tem forças mu vezes o vetor N sub 1 à direita, mu vezes o vetor N sub 2 à direita, o vetor P à esquerda, o vetor T sub i à direita, o vetor N sub 1 verticalmente para baixo, o peso w para baixo e o vetor N sub 2 para cima.
    Figura\(\PageIndex{4}\): (a) Cada bloco se move em velocidade constante. (b) Diagramas de corpo livre para os blocos.

    Estratégia

    Analisamos os movimentos dos dois blocos separadamente. O bloco superior é submetido a uma força de contato exercida pelo bloco inferior. Os componentes dessa força são a força normal N 1 e a força de atrito −0,400 N 1. Outras forças no bloco superior são a tensão T na corda e o peso do próprio bloco superior, 19,6 N. O bloco inferior está sujeito a forças de contato devido ao bloco superior e devido ao piso. A primeira força de contato tem componentes −N 1 e 0,400 N 1, que são simplesmente forças de reação às forças de contato que o bloco inferior exerce no bloco superior. Os componentes da força de contato do piso são N 2 e 0,400 N 2. Outras forças nesse bloco são −P, a tensão T e o peso —39,2 N. Solução Como o bloco superior está se movendo horizontalmente para a direita em velocidade constante, sua aceleração é zero nas direções horizontal e vertical. Da segunda lei de Newton,

    \[\sum F_{x} = m_{2} a_{x}\]

    \[T - 0.400\; N_{1} = 0\]

    \[\sum F_{y} = m_{1} a_{y}\]

    \[N_{1} - 19.6\; N = 0 \ldotp\]

    Resolvendo as duas incógnitas, obtemos N 1 = 19,6 N e T = 0,40 N 1 = 7,84 N. O bloco inferior também não está acelerando, então a aplicação da segunda lei de Newton a esse bloco dá

    \[\sum F_{x} = m_{2} a_{x}\]

    \[T - P + 0.400\; N_{1} + 0.400\; N_{2} = 0\]

    \[\sum F_{y} = m_{1} a_{y}\]

    \[N_{2} - 39.2\; N - N_{1} = 0 \ldotp\]

    Os valores de N 1 e T foram encontrados com o primeiro conjunto de equações. Quando esses valores são substituídos no segundo conjunto de equações, podemos determinar N 2 e P. Eles são

    \[N_{2} = 58.8\; N\; and\; P = 39.2\; N \ldotp\]

    Significância

    Entender em que direção atrair a força de atrito costuma ser problemático. Observe que cada força de atrito indicada na Figura\(\PageIndex{4}\) atua na direção oposta ao movimento de seu bloco correspondente.

    Exemplo\(\PageIndex{3}\): A Crate on an Accelerating Truck

    Uma caixa de 50,0 kg repousa sobre a caçamba de um caminhão, conforme mostrado na Figura\(\PageIndex{5}\). Os coeficientes de atrito entre as superfícies são\(\mu_{k}\) = 0,300 e\(\mu_{s}\) = 0,400. Encontre a força de atrito na caixa quando o caminhão está acelerando em relação ao solo em (a) 2,00 m/s 2 e (b) 5,00 m/s 2.

    A Figura (a) mostra uma ilustração de uma caixa de 50 kg na caçamba de um caminhão. Uma seta horizontal indica uma aceleração, a, para a direita. Um sistema de coordenadas x y é mostrado, com x positivo à direita e y positivo para cima. A Figura (b) mostra o diagrama de corpo livre da caixa. As forças são 490 Newtons verticalmente para baixo, vetor N verticalmente para cima e vetor f horizontalmente para a direita.
    Figura\(\PageIndex{5}\): (a) Uma caixa repousa sobre a caçamba do caminhão que está acelerando para frente. (b) O diagrama de corpo livre da caixa.

    Estratégia

    As forças na caixa são seu peso e as forças normais e de atrito devido ao contato com a caçamba do caminhão. Começamos assumindo que a caixa não está escorregando. Nesse caso, a força de atrito estática fs atua na caixa. Além disso, as acelerações da caixa e do caminhão são iguais.

    Solução
    1. A aplicação da segunda lei de Newton à caixa, usando a estrutura de referência anexada ao solo, produz

      \[\begin{split} \sum F_{x} & = ma_{x} \\ f_{s} & = (50.0\; kg)(2.00\; m/s^{2}) \\ & = 1.00 \times 10^{2}\; N \end{split}\]

      \[\begin{split} \sum F_{y} & = ma_{y} \\ N - 4.90 \times 10^{2}\; N & = (50.0\; kg)(0) \\ N & = 4.90 \times 10^{2}\; N \ldotp \end{split}\]

      Agora podemos verificar a validade de nossa suposição antiderrapante. O valor máximo da força de atrito estático é $$\ mu_ {s} N = (0,400) (4,90\ times 10^ {2}\; N) = 196\; N, $ $ enquanto a força real de atrito estático que atua quando o caminhão acelera para frente a 2,00 m/s 2 é de apenas 1,00 x 10 2 N. Assim, a suposição de não escorregar é válido.

    2. Se a caixa for mover-se com o caminhão quando acelerar a 5,0 m/s 2, a força de atrito estático deve ser $$f_ {s} = ma_ {x} = (50,0\; kg) (5,00\; m/s^ {2}) = 250\; N\ lDotp$$Como isso excede o máximo de 196 N, a caixa deve escorregar. A força de atrito é, portanto, cinética e é $ $ f_ {k} =\ mu_ {k} N = (0,300) (4,90\ times 10^ {2}\; N) = 147\; N\ lDotp$$ A aceleração horizontal da caixa em relação ao solo agora é encontrada a partir de $$\ begin {split}\ sum F_ {x} & = ma_ {x}\ 147; N & = (50,0\; kg) a_ {x},\\ so\; a_ {x} & = 2,94\; m/s ^ {2}\ ldotp\ end {split}\]

    Significância

    Em relação ao solo, o caminhão está acelerando para frente a 5,0 m/s 2 e a caixa está acelerando para frente a 2,94 m/s 2. Portanto, a caixa está deslizando para trás em relação à caçamba do caminhão com uma aceleração de 2,94 m/s 2 − 5,00 m/s 2 = −2,06 m/s 2.

    Exemplo\(\PageIndex{4}\): Snowboarding

    Anteriormente, analisamos a situação de um esquiador em declive se movendo em velocidade constante para determinar o coeficiente de atrito cinético. Agora vamos fazer uma análise similar para determinar a aceleração. O snowboarder da Figure\(\PageIndex{6}\) desliza por uma encosta inclinada em\(\theta\) = 13° em relação à horizontal. O coeficiente de atrito cinético entre a prancha e a neve é\(\mu_{k}\) = 0,20. Qual é a aceleração do snowboarder?

    A Figura (a) mostra uma ilustração de um snowboarder em uma inclinação inclinada a 13 graus acima da horizontal. Uma seta indica uma aceleração, a, inclinação descendente. A Figura (b) mostra o diagrama de corpo livre do snowboarder. As forças são m g cosseno 13 graus na inclinação, perpendicular à superfície, N, fora da inclinação, perpendicular à superfície, m g seno 13 graus descendente paralelo à superfície e mu sub k vezes N, inclinação ascendente paralela à superfície.
    Figura\(\PageIndex{6}\): (a) Um snowboarder desliza por uma encosta inclinada a 13° em relação à horizontal. (b) O diagrama de corpo livre do snowboarder.

    Estratégia

    As forças que atuam no snowboarder são seu peso e a força de contato da encosta, que tem um componente normal à inclinação e um componente ao longo da inclinação (força de atrito cinético). Como ela se move ao longo da inclinação, o quadro de referência mais conveniente para analisar seu movimento é aquele com o eixo x ao longo e o eixo y perpendicular à inclinação. Neste quadro, tanto as forças normais quanto as de atrito estão ao longo dos eixos coordenados, os componentes do peso são mg sin θ ao longo da inclinação e mg cos\(\theta\) em ângulo reto com a inclinação, e a única aceleração é ao longo do eixo x (a y = 0).

    Solução

    Agora podemos aplicar a segunda lei de Newton ao snowboarder:

    \[\begin{split} \sum F_{x} & = ma_{x} \\ mg \sin \theta - \mu_{k} N & = ma_{x} \end{split}\]

    \[\begin{split} \sum F_{y} & = ma_{y} \\ N - mg \cos \theta &= m(0) \ldotp \end{split}\]

    Da segunda equação, N = mg cos\(\theta\). Ao substituir isso na primeira equação, encontramos

    \[\begin{split} a_{x} & = g(\sin \theta - \mu_{k} \cos \theta) \\ & = g(\sin 13^{o} - 0.520 \cos 13^{o}) = 0.29\; m/s^{2} \ldotp \end{split}\]

    Significância

    Observe nessa equação que, se\(\theta\) for pequeno o suficiente ou\(\mu_{k}\) grande o suficiente, um x é negativo, ou seja, o snowboarder fica mais lento.

    Exercício\(\PageIndex{4}\)

    O snowboarder agora está descendo uma colina com inclinação de 10,0°. Qual é a aceleração do esquiador?