4.2: Vetores de deslocamento e velocidade

Last updated
Save as PDF

Page ID: 185299

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

OBJETIVOS DE ENSINO

Calcule vetores de posição em um problema de deslocamento multidimensional.
Resolva o deslocamento em duas ou três dimensões.
Calcule o vetor de velocidade dado o vetor de posição em função do tempo.
Calcule a velocidade média em várias dimensões.

O deslocamento e a velocidade em duas ou três dimensões são extensões diretas das definições unidimensionais. No entanto, agora são quantidades vetoriais, então os cálculos com elas devem seguir as regras da álgebra vetorial, não da álgebra escalar.

Vetor de deslocamento

Para descrever o movimento em duas e três dimensões, devemos primeiro estabelecer um sistema de coordenadas e uma convenção para os eixos. Geralmente usamos as coordenadas$x$,$y$, e$z$ para localizar uma partícula em um ponto$P(x, y, z)$ em três dimensões. Se a partícula estiver se movendo, as variáveis$x$$y$, e$z$ são funções do tempo ($t$):

\[x = x(t) \quad y = y(t) \quad z = z(t) \ldotp \label{4.1}\]

O vetor de posição da origem do sistema de coordenadas até o ponto P é$\vec{r}(t)$. Na notação vetorial unitária, introduzida em Sistemas de Coordenadas e Componentes de um Vetor,$\vec{r}$ (t) é

\[\vec{r} (t) = x(t)\; \hat{i} + y(t)\; \hat{j} + z(t)\; \hat{k} \ldotp \label{4.2}\]

A figura$\PageIndex{1}$ mostra o sistema de coordenadas e o vetor até o ponto$P$, onde uma partícula pode estar localizada em um determinado momento$t$. Observe a orientação dos eixos x, y e z. Essa orientação é chamada de sistema de coordenadas destro e é usada em todo o capítulo.

Um sistema de coordenadas x y z é exibido, com x positivo fora da página, y positivo à direita e z positivo para cima. Um ponto P, com coordenadas x de t, y de t e z de t é mostrado. Todas as coordenadas de P são positivas. O vetor r de t da origem até P também é mostrado como uma seta roxa. As coordenadas x de t, y de t e z de t são mostradas como linhas tracejadas. X de t é um segmento no plano x y, paralelo ao eixo x, y de t é um segmento no plano x y, paralelo ao eixo y e z de t é um segmento paralelo ao eixo z. — Figura$\PageIndex{1}$: Um sistema de coordenadas tridimensional com uma partícula na posição$P(x(t), y(t), z(t))$.

Com nossa definição da posição de uma partícula no espaço tridimensional, podemos formular o deslocamento tridimensional. A figura$\PageIndex{3}$ mostra uma partícula no tempo t ₁ localizada em P ₁ com vetor de posição$\vec{r}$ (t ₁). Posteriormente, t ₂, a partícula está localizada em P ₂ com vetor de posição$\vec{r}$ (t ₂). O vetor de deslocamento$\Delta \vec{r}$ é encontrado$\vec{r}(t_1)$ subtraindo de$\vec{r}(t_2)$:

\[\Delta \vec{r} = \vec{r} (t_{2}) - \vec{r} (t_{1}) \ldotp \label{4.3}\]

A adição de vetores é discutida em Vetores. Observe que essa é a mesma operação que fizemos em uma dimensão, mas agora os vetores estão no espaço tridimensional.

Um sistema de coordenadas x y z é exibido, com x positivo fora da página, y positivo à direita e z positivo para cima. Dois pontos, P 1 e P 2 são mostrados. O vetor r de t 1 da origem até P 1 e o vetor r de t 2 da origem até P 2 são mostrados como setas roxas. O vetor delta r é mostrado como uma seta roxa cuja cauda está em P 1 e cabeça em P 2. — Figura$\PageIndex{2}$: O deslocamento$\Delta \vec{r} = \vec{r}(t_2) − \vec{r}(t_1)$ é o vetor de$P_1$ para$P_2$.

Os exemplos a seguir ilustram o conceito de deslocamento em várias dimensões.

Exemplo 4.1: Satélite de órbita polar

Um satélite está em uma órbita polar circular ao redor da Terra a uma altitude de 400 km, ou seja, ele passa diretamente acima dos pólos norte e sul. Qual é a magnitude e a direção do vetor de deslocamento desde quando ele está diretamente sobre o Pólo Norte até quando está a −45° de latitude?

Estratégia

Fazemos uma imagem do problema para visualizar a solução graficamente. Isso ajudará na nossa compreensão do deslocamento. Em seguida, usamos vetores unitários para resolver o deslocamento.

Solução

A figura$\PageIndex{3}$ mostra a superfície da Terra e um círculo que representa a órbita do satélite. Embora os satélites estejam se movendo no espaço tridimensional, eles seguem trajetórias de elipses, que podem ser representadas graficamente em duas dimensões. Os vetores de posição são desenhados a partir do centro da Terra, que consideramos a origem do sistema de coordenadas, com o eixo y como norte e o eixo x como leste. O vetor entre eles é o deslocamento do satélite. Tomamos o raio da Terra como 6370 km, então o comprimento de cada vetor de posição é de 6770 km.

Um sistema de coordenadas x y, centrado na terra, é mostrado. X positivo está para o leste e positivo y para o norte. Um círculo azul maior e concêntrico com a terra é mostrado. O vetor r de t 1 é uma seta laranja da origem até o local onde o círculo azul cruza o eixo y (90 graus no sentido anti-horário a partir do eixo x positivo). O vetor r de t 2 é uma seta laranja da origem até a localização no círculo azul a menos 45 graus. O vetor delta r é mostrado como uma seta roxa apontando para baixo e para a direita, começando na cabeça do vetor r de t 1 e terminando na cabeça do vetor r de t 2. — Figura$\PageIndex{3}$: Dois vetores de posição são desenhados a partir do centro da Terra, que é a origem do sistema de coordenadas, com o eixo y como norte e o eixo x como leste. O vetor entre eles é o deslocamento do satélite.

Na notação vetorial unitária, os vetores de posição são

\[ \begin{align*} \vec{r}(t_{1}) &= 6770 \ldotp \; km\; \hat{j} \\[4pt] \vec{r}(t_{2}) &= 6770 \ldotp \; km (\cos (-45°))\; \hat{i} + 6770 \ldotp \; km (\sin(−45°))\; \hat{j} \ldotp \end{align*}\]

Avaliando o seno e o cosseno, temos

\[ \begin{align*} \vec{r}(t_{1}) &= 6770 \ldotp \hat{j} \\[4pt] \vec{r}(t_{2}) &= 4787\; \hat{i} − 4787\; \hat{j} \ldotp \end{align*}\]

Agora podemos descobrir$\Delta \vec{r}$ o deslocamento do satélite:

\[\Delta \vec{r} = \vec{r} (t_{2}) - \vec{r} (t_{1}) = 4787\; \hat{i} - 11,557\; \hat{j} \ldotp \nonumber\]

A magnitude do deslocamento é

\[|\Delta \vec{r}| = \sqrt{(4787)^{2} + (-11,557)^{2}} = 12,509\; km. \nonumber\]

O ângulo que o deslocamento faz com o eixo x é

\[\theta = \tan^{-1} \left(\dfrac{-11,557}{4787}\right) = -67.5^{o} \nonumber.\]

Significância

Traçar o deslocamento fornece informações e significado à solução vetorial unitária para o problema. Ao traçar o deslocamento, precisamos incluir seus componentes, bem como sua magnitude e o ângulo que ele faz com o eixo escolhido — nesse caso, o eixo x (Figura$\PageIndex{4}$).

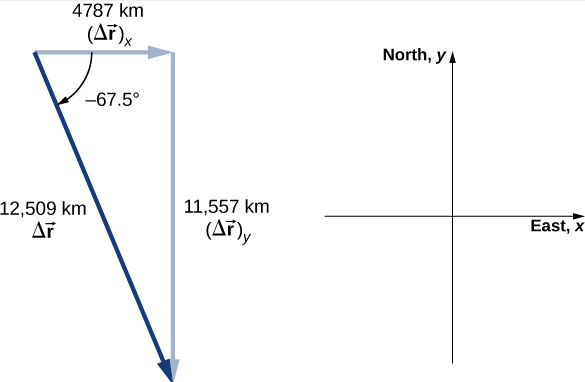
Um sistema de coordenadas x y é mostrado. X positivo está para o leste e positivo y para o norte. O vetor delta r sub x aponta para o leste e tem magnitude 4787 quilômetros. O vetor delta r sub y aponta para o sul e tem magnitude 11.557 quilômetros. O vetor delta r aponta para o sudeste, começando na cauda do delta r sub x e terminando na cabeça do delta r sub y e tem magnitude 12.509 quilômetros. — Figura$\PageIndex{4}$: Vetor de deslocamento com componentes, ângulo e magnitude.

Observe que o satélite percorreu um caminho curvo ao longo de sua órbita circular para ir da posição inicial até a posição final neste exemplo. Também poderia ter viajado 4787 km a leste e depois 11.557 km ao sul para chegar ao mesmo local. Ambos os caminhos são maiores que o comprimento do vetor de deslocamento. Na verdade, o vetor de deslocamento fornece o caminho mais curto entre dois pontos em uma, duas ou três dimensões.

Muitas aplicações em física podem ter uma série de deslocamentos, conforme discutido no capítulo anterior. O deslocamento total é a soma dos deslocamentos individuais, só que desta vez, precisamos ter cuidado, pois estamos adicionando vetores. Ilustramos esse conceito com um exemplo de movimento browniano.

Exemplo 4.2: Movimento browniano

O movimento browniano é um movimento aleatório caótico de partículas suspensas em um fluido, resultante de colisões com as moléculas do fluido. Esse movimento é tridimensional. Os deslocamentos em ordem numérica de uma partícula em movimento browniano podem ter a seguinte aparência, em micrômetros (Figura$\PageIndex{5}$):

\[\Delta \vec{r}_{1} = 2.0\; \hat{i} + \hat{j} + 3.0 \hat{k}\]

\[\Delta \vec{r}_{2} = - \hat{i} + 3.0\; \hat{k}\]

\[\Delta \vec{r}_{3} = 4.0\; \hat{i} -2.0\; \hat{j} + \hat{k}\]

\[\Delta \vec{r}_{4} = -3.0\; \hat{i} + \hat{j} + 3.0\; \hat{k} \ldotp\]

Qual é o deslocamento total da partícula da origem?

Um sistema de coordenadas x y z com distâncias medidas em micrômetros e variando de -10 a +10 micrômetros é mostrado. Os deslocamentos delta r sub 1 é igual a 2 I hat mais j hat mais 2 k hat, delta r sub 2 é igual a -1 I hat mais 3 k hat e delta r sub 3 é igual a -3 I hat mais j hat mais 2 k hat são mostrados como segmentos de linha azul. Vetor r 1 que começa na origem. Cada deslocamento subsequente começa onde termina o anterior. O vetor delta r total é mostrado como uma linha vermelha começando na origem e terminando no final do vetor delta r 4. O delta r total é igual a 2 I hat mais 0 y hat mais 9 k hat. — Figura$\PageIndex{5}$: Trajetória de uma partícula passando por deslocamentos aleatórios do movimento browniano. O deslocamento total é mostrado em vermelho.

Solução

Formamos a soma dos deslocamentos e os adicionamos como vetores:

\[\begin{split} \Delta \vec{r}_{Total} & = \sum \Delta \vec{r}_{i} = \Delta \vec{r}_{1} + \Delta \vec{r}_{2} + \Delta \vec{r}_{3} + \Delta \vec{r}_{4} \\ & = (2.0 - 1.0 + 4.0 - 3.0)\; \hat{i} + (1.0 + 0 - 2.0 + 1.0)\; \hat{j} + (3.0 +3.0 + 1.0 + 2.0)\; \hat{k} \\ & = 2.0\; \hat{i} + 0\; \hat{j} + 9.0\; \hat{k}\; \mu m \ldotp \end{split}\]

Para completar a solução, expressamos o deslocamento como magnitude e direção,

\[| \Delta \vec{r}_{Total}| = \sqrt{2.0^{2} + 0^{2} + 9.0^{2}} = 9.2 \mu m, \quad \theta = \tan^{-1} \left(\dfrac{9}{2}\right) = 77^{o},\]

em relação ao eixo x no plano xz.

Significância

A partir da figura, podemos ver que a magnitude do deslocamento total é menor que a soma das magnitudes dos deslocamentos individuais.

Vetor de velocidade

No capítulo anterior, encontramos a velocidade instantânea calculando a derivada da função de posição em relação ao tempo. Podemos fazer a mesma operação em duas e três dimensões, mas usamos vetores. O vetor de velocidade instantânea é agora

\[\vec{v} (t) = \lim_{\Delta t \rightarrow 0} \frac{\vec{r} (t + \Delta t) - \vec{r} (t)}{\Delta t} = \frac{d \vec{r}}{dt} \ldotp \label{4.4}\]

Vamos examinar graficamente a orientação relativa do vetor de posição e do vetor de velocidade. Na Figura,$\PageIndex{6}$ mostramos os vetores$\vec{r}$ (t) e$\vec{r}$ (t +$\Delta$ t), que fornecem a posição de uma partícula se movendo ao longo de um caminho representado pela linha cinza. Quando$\Delta$ t vai para zero, o vetor de velocidade, dado pela Equação\ ref {4.4}, torna-se tangente ao caminho da partícula no tempo t.

Os vetores r de t e r de t mais delta t são mostrados como setas vermelhas no sistema de coordenadas x y. Ambos os vetores começam na origem. O vetor delta r aponta da cabeça do vetor r de t até a cabeça do vetor r de t mais delta t. — Figura$\PageIndex{6}$: Uma partícula se move ao longo de um caminho dado pela linha cinza. No limite, quando$\Delta$ t se aproxima de zero, o vetor de velocidade se torna tangente ao caminho da partícula.

A equação\ ref {4.4} também pode ser escrita em termos dos componentes de$\vec{v}$ (t). Desde

\[\vec{r} (t) = x(t)\; \hat{i} + y(t)\; \hat{j} + z(t)\; \hat{k},\]

podemos escrever

\[\vec{v} (t) = v_{x} (t)\; \hat{i} + v_{y} (t)\; \hat{j} + v_{z} (t)\; \hat{k} \label{4.5}\]

onde

\[v_{x} (t) = \frac{dx(t)}{dt}, \quad v_{y} (t) = \frac{dy(t)}{dt}, \quad v_{z} (t) = \frac{dz(t)}{dt} \ldotp \label{4.6}\]

Se apenas a velocidade média é preocupante, temos o equivalente vetorial da velocidade média unidimensional para duas e três dimensões:

\[\vec{v}_{avg} = \frac{\vec{r} (t_{2}) - \vec{r} (t_{1})}{t_{2} - t_{1}} \ldotp \label{4.7}\]

Exemplo 4.3: Calculando o vetor de velocidade

A função de posição de uma partícula é$\vec{r}$ (t) = 2,0t ²$\hat{i}$ + (2,0 + 3,0t)$\hat{j}$ + 5,0t$\hat{k}$ m. (a) Qual é a velocidade instantânea e a velocidade em t = 2,0 s? (b) Qual é a velocidade média entre 1,0 s e 3,0 s?

Solução

Usando a Equação\ ref {4.5} e a Equação\ ref {4.6}, e tomando a derivada da função de posição em relação ao tempo, encontramos

$$v (t) =\ frac {d\ vec {r} (t)} {dt} = 4,0t\;\ hat {i} + 3,0\;\ hat {j} + 5,0\;\ hat {k}\; m/s$$$$\ vec {v} (2,0\; s) = 8,0\;\ hat {i} + 3,0\;\ hat {j} + 5,0;\ hat {k}\; M/S$$$$velocidade\; |\ vec {v} (2,0\; s) | =\ sqrt {8^ {2} + 3^ {2} + 5^ {2}} = 9,9\; m/s\ ldotp$$
Da equação\ ref {4.7}, $$\ begin {split}\ vec {v} _ {avg} & =\ frac {\ vec {r} (t_ {2}) -\ vec {r} (t_ {1})} {t_ {2} - t_ {1}} =\ frac {\ vec {r} (3,0\; s) -\ vec {r} (1,0\; s)} {3,0\; s - 1,0\; s} =\ frac {(18\;\ hat {i} + 11\;\ hat {j} + 15\;\ hat {k}) m - (2\;\ hat {i} + 5\;\ hat {j} + 5\;\ hat {k}) m} {2.0\; s}\\ & =\ frac {( 16\;\ hat {i} + 6\;\ hat {j} + 10\;\ hat {k}) m} {2.0\; s} = 8,0\;\ hat {i} + 3,0\;\ hat {j} + 5,0\;\ hat {k}\; m/s\ ldotp\ end {split} $$

Significância

Vemos que a velocidade média é a mesma que a velocidade instantânea em t = 2,0 s, como resultado da função de velocidade ser linear. Isso não precisa ser o caso em geral. Na verdade, na maioria das vezes, as velocidades instantâneas e médias não são as mesmas.

Exercício 4.1

A função de posição de uma partícula é$\vec{r}$ (t) = 3,0t ³$\hat{i}$ + 4,0$\hat{j}$. (a) Qual é a velocidade instantânea em t = 3 s? (b) A velocidade média entre 2 s e 4 s é igual à velocidade instantânea em t = 3 s?

A independência dos movimentos perpendiculares

Quando observamos as equações tridimensionais de posição e velocidade escritas em notação vetorial unitária, Equação\ ref {4.2} e Equação\ ref {4.5}, vemos que os componentes dessas equações são funções separadas e únicas do tempo que não dependem umas das outras. O movimento ao longo da direção x não faz parte de seu movimento nas direções y e z, e da mesma forma para os outros dois eixos coordenados. Assim, o movimento de um objeto em duas ou três dimensões pode ser dividido em movimentos separados e independentes ao longo dos eixos perpendiculares do sistema de coordenadas no qual o movimento ocorre.

Para ilustrar esse conceito com relação ao deslocamento, considere uma mulher caminhando do ponto A ao ponto B em uma cidade com quarteirões quadrados. A mulher que segue o caminho de A a B pode caminhar para o leste por muitos quarteirões e depois para o norte (duas direções perpendiculares) até outro conjunto de blocos chegar a B. A distância que ela caminha para o leste é afetada apenas por seu movimento para o leste. Da mesma forma, a distância que ela caminha para o norte é afetada apenas por seu movimento para o norte.

Independência do movimento

Na descrição cinemática do movimento, podemos tratar os componentes horizontal e vertical do movimento separadamente. Em muitos casos, o movimento na direção horizontal não afeta o movimento na direção vertical e vice-versa.

Um exemplo que ilustra a independência dos movimentos verticais e horizontais é dado por duas bolas de beisebol. Uma bola de beisebol é retirada do repouso. No mesmo instante, outro é lançado horizontalmente da mesma altura e segue um caminho curvo. Um estroboscópio captura as posições das bolas em intervalos de tempo fixos à medida que elas caem (Figura$\PageIndex{7}$).

Duas bolas idênticas são ilustradas em 5 locais em intervalos de tempo iguais. As bolas começam na mesma posição vertical. As setas verdes representam as velocidades horizontais e as setas roxas representam as velocidades verticais em cada posição. A bola à direita tem uma velocidade horizontal inicial, enquanto a bola à esquerda não tem velocidade horizontal. O movimento horizontal é a velocidade horizontal constante em todos os momentos para ambas as bolas. O movimento vertical é uma aceleração vertical constante. A velocidade vertical de cada bola está aumentando em magnitude e apontando para baixo. A cada instante, ambas as bolas têm posições verticais e velocidades verticais idênticas. — Figura$\PageIndex{7}$: Um diagrama dos movimentos de duas bolas idênticas: uma cai do repouso e a outra tem uma velocidade horizontal inicial. Cada posição subsequente é um intervalo de tempo igual. As setas representam as velocidades horizontal e vertical em cada posição. A bola à direita tem uma velocidade horizontal inicial, enquanto a bola à esquerda não tem velocidade horizontal. Apesar da diferença nas velocidades horizontais, as velocidades e posições verticais são idênticas para ambas as bolas, o que mostra que os movimentos vertical e horizontal são independentes.

É notável que, para cada flash do estroboscópio, as posições verticais das duas bolas sejam as mesmas. Essa semelhança implica que o movimento vertical é independente de a bola estar se movendo horizontalmente. (Supondo que não haja resistência do ar, o movimento vertical de um objeto em queda é influenciado somente pela gravidade, não por nenhuma força horizontal.) Um exame cuidadoso da bola lançada horizontalmente mostra que ela percorre a mesma distância horizontal entre os flashes. Isso ocorre porque não há forças adicionais na bola na direção horizontal depois que ela é lançada. Esse resultado significa que a velocidade horizontal é constante e não é afetada nem pelo movimento vertical nem pela gravidade (que é vertical). Observe que este caso é válido apenas para condições ideais. No mundo real, a resistência do ar afeta a velocidade das bolas em ambas as direções.

O caminho curvo bidimensional da bola lançada horizontalmente é composto por dois movimentos unidimensionais independentes (horizontal e vertical). A chave para analisar esse movimento, chamado movimento de projétil, é resolvê-lo em movimentos ao longo das direções perpendiculares. Resolver o movimento bidimensional em componentes perpendiculares é possível porque os componentes são independentes.