13.4: Emf emocional
- Page ID
- 184558
Ao final desta seção, você poderá:
- Determine a magnitude de um emf induzido em um fio que se move a uma velocidade constante através de um campo magnético
- Discuta exemplos que usam emf mocional, como uma pistola ferroviária e um satélite conectado
O fluxo magnético depende de três fatores: a intensidade do campo magnético, a área pela qual as linhas do campo passam e a orientação do campo com a área da superfície. Se alguma dessas quantidades variar, ocorre uma variação correspondente no fluxo magnético. Até agora, consideramos apenas as mudanças de fluxo devido a uma mudança de campo. Agora, analisamos outra possibilidade: uma mudança de área pela qual as linhas de campo passam, incluindo uma mudança na orientação da área.
Dois exemplos desse tipo de mudança de fluxo estão representados na Figura\(\PageIndex{1}\). Em parte (a), o fluxo através do circuito retangular aumenta à medida que ele se move para o campo magnético e, em parte (b), o fluxo através da bobina rotativa varia com o ângulo\(\theta\).
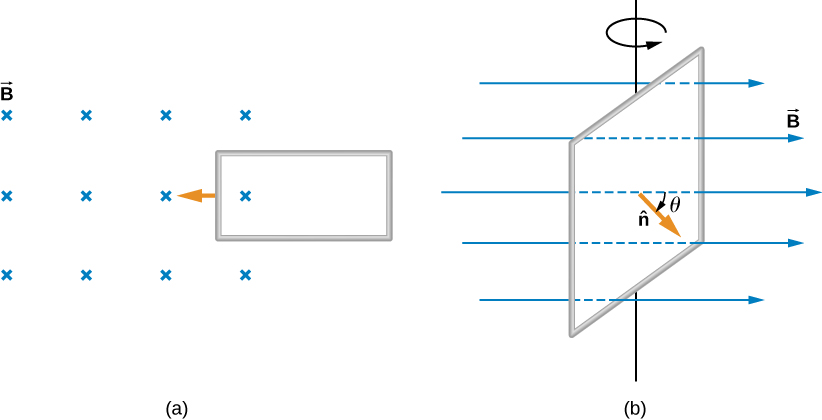
É interessante observar que o que percebemos como a causa de uma determinada mudança de fluxo, na verdade, depende do quadro de referência que escolhemos. Por exemplo, se você estiver em repouso em relação às bobinas móveis da Figura\(\PageIndex{1b}\), verá o fluxo variar devido a uma mudança no campo magnético — em parte (a), o campo se move da esquerda para a direita em seu quadro de referência e, em parte (b), o campo está girando. Muitas vezes, é possível descrever uma mudança de fluxo por meio de uma bobina que está se movendo em um quadro de referência específico em termos de mudança de campo magnético em um segundo quadro, onde a bobina é estacionária. No entanto, as questões do quadro de referência relacionadas ao fluxo magnético estão além do nível deste livro didático. Evitaremos essas complexidades sempre trabalhando em uma estrutura em repouso em relação ao laboratório e explicaremos as variações de fluxo como decorrentes de uma mudança de campo ou de uma área em mudança.
Agora vamos ver uma haste condutora puxada em um circuito, alterando o fluxo magnético. A área delimitada pelo circuito 'MNOP' da Figura\(\PageIndex{2}\) é lx e é perpendicular ao campo magnético, então podemos simplificar a\(\Phi_{\mathrm{m}}=\int_{S} \overrightarrow{\mathbf{B}} \cdot \hat{\mathbf{n}} d A\) integração de em uma multiplicação do campo magnético e da área. O fluxo magnético através da superfície aberta é, portanto,
\[\Phi_m = Blx.\]
Como B e l são constantes e a velocidade da haste é\(v = dx/dt\), agora podemos reafirmar a lei de Faraday, Equação 13.2.2, para a magnitude da emf em termos da haste condutora móvel como
\[\epsilon = \frac{d\Phi_m}{dt} = Bl \frac{dx}{dt} = Blv.\]
A corrente induzida no circuito é o emf dividido pela resistência ou
\[I = \frac{Blv}{R}.\]
Além disso, a direção do emf induzido satisfaz a lei de Lenz, como você pode verificar pela inspeção da figura.
Este cálculo de emf induzido mocionalmente não se restringe a uma haste que se move em trilhos condutores. Com\(\vec{F} = q\vec{v} \times \vec{B}\) como ponto de partida, pode-se demonstrar que\(\epsilon = - d\Phi_m/dt\) vale para qualquer alteração no fluxo causada pelo movimento de um condutor. Vimos na Lei de Faraday que o emf induzido por um campo magnético variável no tempo obedece a essa mesma relação, que é a lei de Faraday. Assim, a lei de Faraday vale para todas as mudanças de fluxo, sejam elas produzidas por um campo magnético variável, por movimento ou por uma combinação das duas.
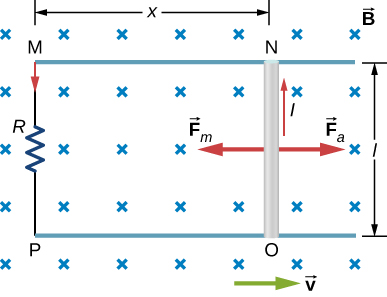
Do ponto de vista da energia\(F_a v\),\(\vec{F}_a\) produz energia e o resistor dissipa a energia\(I^2R\). Como a haste está se movendo em velocidade constante, a força aplicada\(F_a\) deve equilibrar a força magnética\(F_m = IlB\) na haste quando ela está carregando a corrente induzida I. Assim, a energia produzida é
\[F_av = IlBv = \frac{Blv}{R} \cdot lBv = \frac{l^2B^2v^2}{R}.\]
A energia dissipada é
\[P = I^2R = \left(\frac{Blv}{R}\right)^2 R = \frac{l^2B^2v^2}{R}.\]
Ao satisfazer o princípio da conservação de energia, os poderes produzidos e dissipados são iguais.
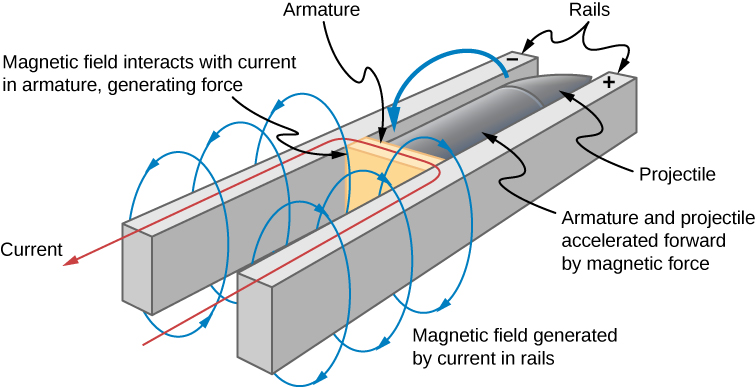
Esse princípio pode ser visto na operação de uma pistola ferroviária. Uma pistola ferroviária é um lançador de projéteis eletromagnéticos que usa um aparelho semelhante à Figura\(\PageIndex{2}\) e é mostrado de forma esquemática na Figura\(\PageIndex{3}\). A haste condutora é substituída por um projétil ou arma a ser disparada. Até agora, só ouvimos falar sobre como o movimento causa um EMF. Em um canhão ferroviário, o desligamento/redução ideal de um campo magnético diminui o fluxo entre os trilhos, fazendo com que uma corrente flua na haste (armadura) que segura o projétil. Essa corrente através da armadura experimenta uma força magnética e é impulsionada para frente. Os canhões ferroviários, no entanto, não são amplamente usados nas forças armadas devido ao alto custo de produção e às altas correntes: quase um milhão de amperes são necessários para produzir energia suficiente para que um canhão ferroviário seja uma arma eficaz.
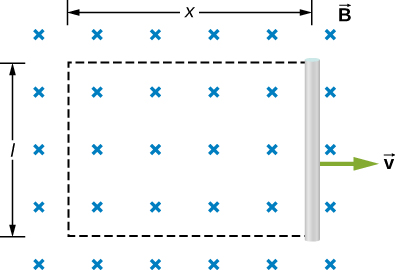
Podemos calcular um emf induzido mocionalmente com a lei de Faraday mesmo quando um circuito fechado real não está presente. Simplesmente imaginamos uma área fechada cujo limite inclui o condutor móvel, calculamos e\(\Phi_m\), em seguida, encontramos o emf da lei de Faraday. Por exemplo, podemos deixar que a haste móvel da Figura\(\PageIndex{4}\) seja um lado da área retangular imaginária representada pelas linhas tracejadas. A área do retângulo é lx, então o fluxo magnético através dele é\(\Phi_m = Blx\). Diferenciando essa equação, obtemos
\[\frac{d\Phi_m}{dt} = Bl\frac{dx}{dt} = Blv,\]
que é idêntica à diferença de potencial entre as extremidades da haste que determinamos anteriormente.
Os eletromagnéticos mocionais no campo magnético fraco da Terra normalmente não são muito grandes, ou notaríamos voltagem ao longo de hastes de metal, como uma chave de fenda, durante movimentos comuns. Por exemplo, um cálculo simples da emf de movimento de uma haste de 1,0 m movendo-se a 3,0 m/s perpendicularmente ao campo da Terra fornece
\[emf = Blv = (5.0 \times 10^{-5} T)(1.0 \, m)(3.0 \, m/s) = 150 \, \mu V.\]
Esse pequeno valor é consistente com a experiência. No entanto, há uma exceção espetacular. Em 1992 e 1996, foram feitas tentativas com o ônibus espacial para criar grandes emfs emocionais. O satélite conectado deveria ser liberado em um comprimento de fio de 20 km, conforme mostrado na Figura\(\PageIndex{5}\), para criar um emf de 5 kV movendo-se em velocidade orbital pelo campo da Terra. Esse emf pode ser usado para converter parte da energia cinética e potencial do ônibus espacial em energia elétrica se um circuito completo pudesse ser feito. Para completar o circuito, a ionosfera estacionária deveria fornecer um caminho de retorno através do qual a corrente pudesse fluir. (A ionosfera é a atmosfera rarefeita e parcialmente ionizada em altitudes orbitais. Ele conduz por causa da ionização. A ionosfera tem a mesma função que os trilhos estacionários e o resistor de conexão na Figura\(\PageIndex{3}\), sem os quais não haveria um circuito completo.) Arrastar a corrente no cabo devido à força magnética\(F = IlBsin \, \theta\) faz o trabalho que reduz a energia cinética e potencial da lançadeira e permite que ela seja convertida em energia elétrica. Ambos os testes não tiveram sucesso. No primeiro, o cabo desligou e só podia ser estendido por algumas centenas de metros; no segundo, o cabo quebrou quando estava quase totalmente estendido. O exemplo\(\PageIndex{1}\) indica viabilidade em princípio.
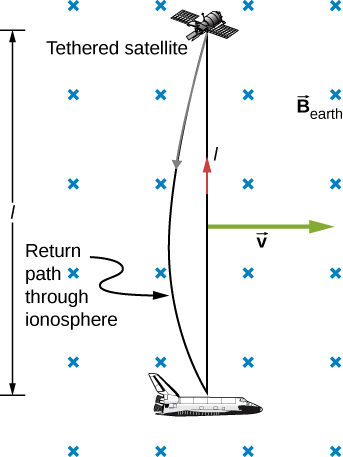
Calcule o emf mocional induzido ao longo de um condutor de 20,0 km movendo-se a uma velocidade orbital de 7,80 km/s perpendicular ao campo\(5.00 \times 10^{-5} T\) magnético da Terra.
Estratégia
Esse é um ótimo exemplo de uso da equação mocional\(\epsilon = Blv\).
Solução
Inserindo os valores fornecidos em\(\epsilon = Blv\) dá
\[\epsilon = Blv\]
\[= (5.00 \times 10^{-5}T)(2.00 \times 10^4 \, m)(7.80 \times 10^3 \, m/s)\]
\[= 7.80 \times 10^3 \, V.\]
Significância
O valor obtido é maior do que a tensão medida de 5 kV para o experimento de lançadeira, uma vez que o movimento orbital real da corda não é perpendicular ao campo terrestre. O valor de 7,80 kV é o emf máximo obtido quando\(\theta = 90^o\) e assim por diante\(sin \, \theta = 1\).
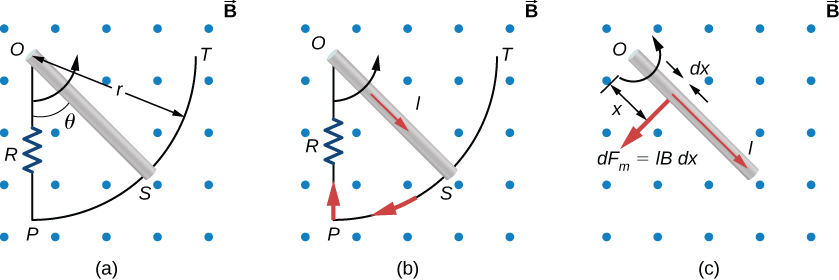
A parte (a) da Figura\(\PageIndex{6}\) mostra uma haste de metal OS que está girando em um plano horizontal em torno do ponto O. A haste desliza ao longo de um fio que forma um arco circular PST de raio r. O sistema está em um campo magnético constante\(\vec{B}\) que é direcionado para fora da página. (a) Se você girar a haste a uma velocidade angular constante\(\omega\), qual é a corrente I no OPSO de circuito fechado? Suponha que o resistor R forneça toda a resistência no circuito fechado. (b) Calcule o trabalho por unidade de tempo que você faz ao girar a haste e mostre que é igual à potência dissipada no resistor.
Estratégia
O fluxo magnético é o campo magnético multiplicado pela área do quarto de círculo ou\(A = r^2 \theta/2\). Ao encontrar o emf por meio da lei de Faraday, todas as variáveis são constantes no tempo\(\theta\), mas, com\(\omega = d\theta/dt\). Para calcular o trabalho por unidade de tempo, sabemos que isso está relacionado ao torque vezes a velocidade angular. O torque é calculado conhecendo a força em uma haste e integrando-a ao longo do comprimento da haste.
Solução
- Da geometria, a área do loop OPSO é\(A = \frac{r^2\theta}{2}\). Portanto, o fluxo magnético através do circuito é\[\Phi_m = BA = B\frac{r^2\theta}{2}.\] diferenciado em relação ao tempo e ao uso\(\omega = d\theta/dt\), temos\[\epsilon = \left|\frac{d\Phi_m}{dt}\right| = \frac{Br^2\omega}{2}.\] Quando dividido pela resistência R do loop, isso resulta na magnitude da corrente induzida.\[I = \frac{\epsilon}{R} = \frac{Br^2\omega}{2R}.\] À medida que\(\theta\) aumenta, o mesmo acontece com o fluxo o loop devido\(\vec{B}\) a. Para neutralizar esse aumento, o campo magnético devido à corrente induzida deve ser direcionado para a página na região delimitada pelo circuito. Portanto, como a parte (b) da Figura\(\PageIndex{6}\) ilustra, a corrente circula no sentido horário.
- Você gira a haste exercendo um torque nela. Como a haste gira em velocidade angular constante, esse torque é igual e oposto ao torque exercido sobre a corrente na haste pelo campo magnético original. A força magnética no segmento infinitesimal de comprimento dx mostrada na parte (c) da Figura\(\PageIndex{6}\) é\(dF_m = IBdx\), então o torque magnético neste segmento é\[d\tau_m = x \cdot dF_m = IBxdx.\] O torque magnético líquido na haste é então\[\tau_m = \int_0^r d\tau_m = IB \int_0^r x \, dx = \frac{1}{2}IBr^2.\] O torque\(\tau\) que você exerce na haste é igual e oposto a \(\tau_m\), e o trabalho que você faz quando a haste gira em um ângulo\(d\theta\) é\(dW = rd\theta\). Portanto, o trabalho por unidade de tempo que você faz na haste é\[\frac{dW}{dt} = \tau\frac{d\theta}{dt} = \frac{1}{2} IBr^2 \frac{d\theta}{dt} = \frac{1}{2} \left(\frac{Br^2\omega}{2R}\right) Br^2\omega = \frac{B^2r^4\omega^2}{4R},\] onde substituímos por I. A potência dissipada no resistor é\(P = IR^2\), que pode ser escrita como\[P = \left(\frac{Br^2\omega}{2R}\right)^2 R = \frac{B^2r^4\omega^2}{4R}.\] Portanto, vemos que,\[P = \frac{dW}{dt}.\] portanto, a potência dissipada no resistor é igual ao trabalho por unidade de tempo realizado na rotação da haste.
Significância
Uma forma alternativa de observar o emf induzido pela lei de Faraday é integrar-se no espaço em vez do tempo. A solução, no entanto, seria a mesma. O emf emocional é
\[|\epsilon| = \int Bvdl.\]
A velocidade pode ser escrita como a velocidade angular vezes o raio e o comprimento diferencial escrito como dr. Portanto,
\[\epsilon| = B\int vdr = B\omega \int_0^l rdr = \frac{1}{2} B\omega l^2,\]que é a mesma solução de antes.
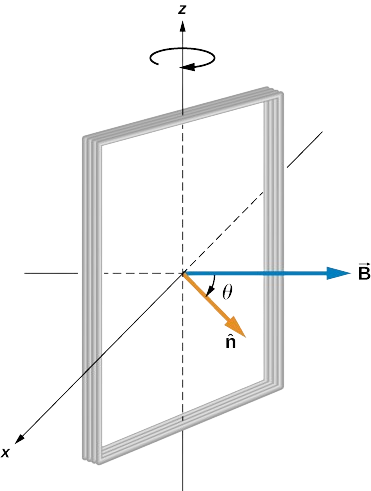
Uma bobina retangular de curvas da área A e N é colocada em um campo magnético uniforme\(\vec{B} = B\hat{j}\), conforme mostrado na Figura\(\PageIndex{7}\). A bobina é girada em torno do eixo z através de seu centro a uma velocidade angular constante\(\omega\). Obtenha uma expressão para o emf induzido na bobina.
Estratégia
De acordo com o diagrama, o ângulo entre a perpendicular à superfície ((\ hat {n}\)) e o campo magnético\((\vec{B})\) é\(\theta\). O produto escalar do\(B \cdot \hat{n}\) simplifica apenas para o\(cos \, \theta\) componente do campo magnético, ou seja, onde o campo magnético se projeta no vetor de área unitária\(\hat{n}\). A magnitude do campo magnético e a área do circuito são fixadas ao longo do tempo, o que simplifica rapidamente a integração. O emf induzido é escrito usando a lei de Faraday.
Solução
Quando a bobina está em uma posição tal que seu vetor normal\(\hat{n}\) faz um ângulo\(\theta\) com o campo magnético,\(\vec{B}\) o fluxo magnético através de uma única volta da bobina é
\[\Phi_m = \int_S \vec{B} \cdot \hat{n} dA = BA \, cos \, \theta.\]
Da lei de Faraday, o emf induzido na bobina é
\[\epsilon = - N\frac{d\Phi_m}{dt} = NB A \, sin \, \theta \frac{d\theta}{dt}.\]
A velocidade angular constante é\(\omega = d\theta /dt\). O ângulo\(\theta\) representa a evolução temporal da velocidade angular ou\(\omega t\). Isso muda a função para espaço de tempo em vez de\(\theta\). O emf induzido, portanto, varia sinusoidalmente com o tempo, de acordo com
\[\epsilon = \epsilon_0 \, sin \, \omega t,\]onde\(\epsilon_0 = NBA \omega\).
Significância
Se a intensidade do campo magnético ou a área do loop também estivessem mudando com o tempo, essas variáveis não seriam capazes de ser extraídas da derivada de tempo para simplesmente a solução, conforme mostrado. Este exemplo é a base para um gerador elétrico, pois faremos uma discussão completa em Aplicações da Lei de Newton.
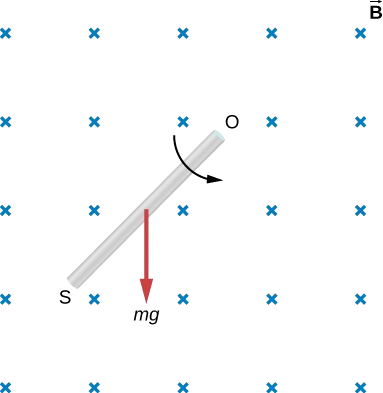
Abaixo, é mostrada uma haste de comprimento l que é girada no sentido anti-horário em torno do eixo através de O pelo torque devido\(m\vec{g}\) a. Supondo que a haste esteja em um campo magnético uniforme\(\vec{B}\), qual é o emf induzido entre as extremidades da haste quando sua velocidade angular é\(\omega\)? Qual extremidade da haste tem um potencial maior?
- Resposta
-


