13.3: Lei de Lenz

Objetivos de

Ao final desta seção, você poderá:

• Use a lei de Lenz para determinar a direção do emf induzido sempre que um fluxo magnético muda
• Use a lei de Faraday com a lei de Lenz para determinar o emf induzido em uma bobina e em um solenóide

A direção na qual o emf induzido aciona a corrente em torno de um circuito de arame pode ser encontrada através do sinal negativo. No entanto, geralmente é mais fácil determinar essa direção com a lei de Lenz, nomeada em homenagem a seu descobridor, Heinrich Lenz (1804-1865). (Faraday também descobriu essa lei, independentemente de Lenz.) Declaramos a lei de Lenz da seguinte forma:

Lei de Lenz

A direção do emf induzido aciona a corrente em torno de um circuito de arame para sempre se opor à mudança no fluxo magnético que causa o emf.

A lei de Lenz também pode ser considerada em termos de conservação de energia. Se empurrar um ímã em uma bobina causar corrente, a energia dessa corrente deve ter vindo de algum lugar. Se a corrente induzida causar um campo magnético oposto ao aumento do campo do ímã que inserimos, a situação é clara. Empurramos um ímã contra um campo e trabalhamos no sistema, que apareceu como corrente. Se não fosse o caso de o campo induzido se opor à mudança no fluxo, o ímã seria puxado para produzir uma corrente sem que nada funcionasse. A energia potencial elétrica teria sido criada, violando a conservação da energia.

Para determinar um emf induzido\(\epsilon\), você primeiro calcula o fluxo magnético\(\Phi_m\) e depois obtém\(d\Phi_m/dt\). A magnitude de\(\epsilon\) é dada por

\[\epsilon = \left|\dfrac{d\Phi_m}{dt}\right|.\]

Finalmente, você pode aplicar a lei de Lenz para determinar o sentido de\(\epsilon\). Isso será desenvolvido por meio de exemplos que ilustram a seguinte estratégia de resolução de problemas.

Estratégia de resolução de problemas: Lei de Lenz

Para usar a lei de Lenz para determinar as direções dos campos magnéticos induzidos, correntes e emfs:

• Faça um esboço da situação para usar na visualização e gravação de direções.
• Determine a direção do campo magnético aplicado\(\vec{B}\).
• Determine se seu fluxo magnético está aumentando ou diminuindo.
• Agora determine a direção do campo magnético induzido\(\vec{B}\). O campo magnético induzido tenta reforçar um fluxo magnético que está diminuindo ou se opõe a um fluxo magnético que está aumentando. Portanto, o campo magnético induzido soma ou subtrai o campo magnético aplicado, dependendo da mudança no fluxo magnético.
• Use a regra 2 do lado direito (RHR-2; veja Forças e Campos Magnéticos) para determinar a direção da corrente induzida I que é responsável pelo campo magnético induzido\(\vec{B}\).
• A direção (ou polaridade) do emf induzido agora pode acionar uma corrente convencional nessa direção.

Vamos aplicar a lei de Lenz ao sistema da Figura\(\PageIndex{1a}\). Designamos a “frente” do circuito condutor fechado como a região que contém a barra magnética que se aproxima e a “parte traseira” do circuito como a outra região. À medida que o pólo norte do ímã se move em direção ao circuito, o fluxo através do circuito devido ao campo do ímã aumenta porque a força das linhas de campo direcionadas da frente para a parte de trás do circuito está aumentando. Portanto, uma corrente é induzida no circuito. Pela lei de Lenz, a direção da corrente induzida deve ser tal que seu próprio campo magnético seja direcionado de forma a se opor à mudança de fluxo causada pelo campo do ímã que se aproxima. Portanto, a corrente induzida circula de forma que suas linhas de campo magnético através do circuito sejam direcionadas de trás para a frente do circuito. Com o RHR-2, coloque o polegar apontando contra as linhas do campo magnético, que estão em direção à barra magnética. Seus dedos se enrolam no sentido anti-horário, conforme visto da barra magnética. Alternativamente, podemos determinar a direção da corrente induzida tratando o circuito de corrente como um eletroímã que se opõe à aproximação do pólo norte da barra magnética. Isso ocorre quando a corrente induzida flui conforme mostrado, pois então a face do circuito mais próxima do ímã que se aproxima também é um pólo norte.

Figura\(\PageIndex{1}\): A mudança no fluxo magnético causada pela aproximação do ímã induz uma corrente no circuito. (a) Um pólo norte que se aproxima induz uma corrente no sentido anti-horário em relação à barra magnética. (b) Um pólo sul que se aproxima induz uma corrente no sentido horário em relação à barra magnética.

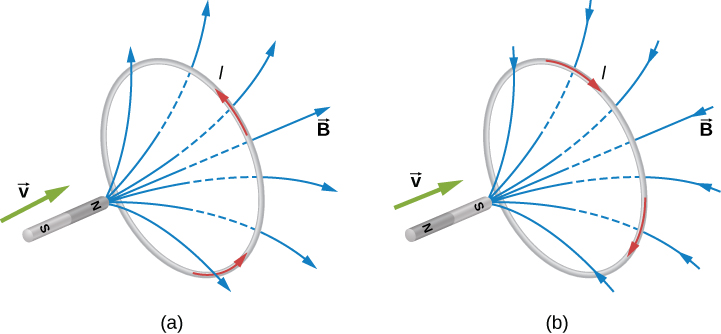
A parte (b) da figura mostra o polo sul de um ímã se movendo em direção a um circuito condutor. Nesse caso, o fluxo através do circuito devido ao campo do ímã aumenta porque o número de linhas de campo direcionadas da parte traseira para a frente do circuito está aumentando. Para se opor a essa mudança, uma corrente é induzida no circuito cujas linhas de campo através do loop são direcionadas da frente para trás. Equivalentemente, podemos dizer que a corrente flui em uma direção de forma que a face do circuito mais próxima do ímã que se aproxima seja um pólo sul, que então repele o pólo sul que se aproxima do ímã. Com o RHR-2, seu polegar aponta para longe da barra magnética. Seus dedos se enrolam no sentido horário, que é a direção da corrente induzida.

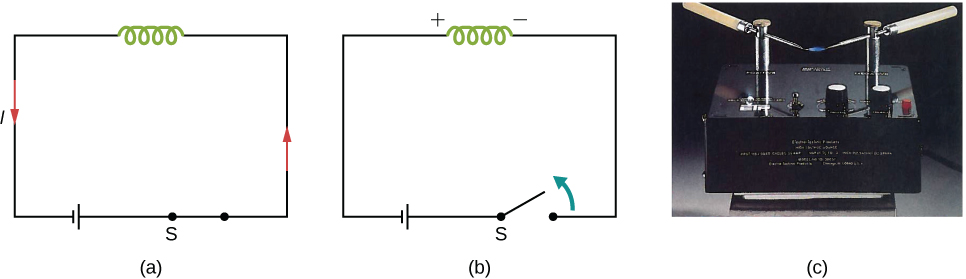
Outro exemplo ilustrando o uso da lei de Lenz é mostrado na Figura\(\PageIndex{2}\). Quando o interruptor é aberto, a diminuição da corrente através do solenóide causa uma diminuição no fluxo magnético através de suas bobinas, o que induz um emf no solenóide. Esse emf deve se opor à mudança (o término da corrente) que a causa. Consequentemente, o emf induzido tem a polaridade mostrada e dirige na direção da corrente original. Isso pode gerar um arco nos terminais do switch quando ele é aberto.

Figura\(\PageIndex{2}\): (a) Um solenóide conectado a uma fonte de emf. (b) A chave de abertura S encerra a corrente, que por sua vez induz um emf no solenóide. (c) Uma diferença de potencial entre as extremidades das hastes pontiagudas é produzida pela indução de um emf em uma bobina. Essa diferença de potencial é grande o suficiente para produzir um arco entre as pontas afiadas.

Exercício\(\PageIndex{1A}\)

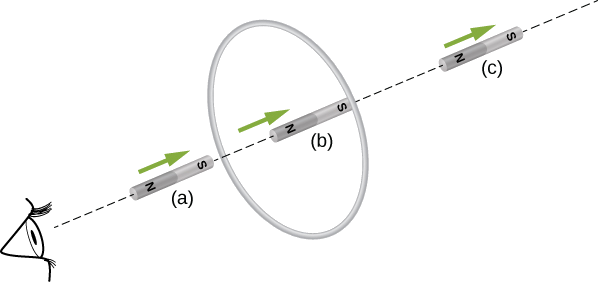
Encontre a direção da corrente induzida no circuito de arame mostrado abaixo quando o ímã entra, passa e sai do circuito.

Solução

Para o observador mostrado, a corrente flui no sentido horário à medida que o ímã se aproxima, diminui para zero quando o ímã está centrado no plano da bobina e, em seguida, flui no sentido anti-horário quando o ímã sai da bobina.

Exercício\(\PageIndex{1B}\)

Verify the directions of the induced currents in Figure 13.2.2.

Example \(\PageIndex{1A}\): A Circular Coil in a Changing Magnetic Field

A magnetic field \(\vec{B}\) is directed outward perpendicular to the plane of a circular coil of radius \(r = 0.50 \, m\) (Figure \(\PageIndex{3}\)). The field is cylindrically symmetrical with respect to the center of the coil, and its magnitude decays exponentially according to \(B = (1.5T)e^{(5.0s^{-1})t}\), where B is in teslas and t is in seconds. (a) Calculate the emf induced in the coil at the times \(t_1 = 0\), \(t_2 = 5.0 \times 10^{-2}s\), and \(t_3 = 1.0 \, s\). (b) Determine the current in the coil at these three times if its resistance is \(10 \, \Omega\).

Figure \(\PageIndex{3}\): A circular coil in a decreasing magnetic field.

Strategy

Since the magnetic field is perpendicular to the plane of the coil and constant over each spot in the coil, the dot product of the magnetic field \(\vec{B}\) and normal to the area unit vector \(\hat{n}\) turns into a multiplication. The magnetic field can be pulled out of the integration, leaving the flux as the product of the magnetic field times area. We need to take the time derivative of the exponential function to calculate the emf using Faraday’s law. Then we use Ohm’s law to calculate the current.

Solution

1. Since \(\vec{B}\) is perpendicular to the plane of the coil, the magnetic flux is given by \[\Phi_m = B\pi r^2 = (1.5 e^{-5.0 t}T)\pi (0.50 \, m)^2\]\[= 1.2 e^{-(5.0 s^{-1})t} Wb.\] From Faraday’s law, the magnitude of the induced emf is \[\epsilon = \left|\frac{d\Phi_m}{dt}\right| = \left|\frac{d}{dt} (1.2 e^{-(5.0s^{-1})t} Wb)\right| = 6.0 e^{-(5.0s^{-1})t}V.\] Since \(\vec{B}\) is directed out of the page and is decreasing, the induced current must flow counterclockwise when viewed from above so that the magnetic field it produces through the coil also points out of the page. For all three times, the sense of ε is counterclockwise; its magnitudes are \[\epsilon (t_1) = 6.0 V; \, \epsilon (t_2) = 4.7 \, V; \, \epsilon (t_3) = 0040 \, V.\]
2. From Ohm’s law, the respective currents are \[I(t_1) = \frac{\epsilon (t_1)}{R} = \frac{6.0 \, V}{10 \, \Omega} = 0.60 \, A;\]\[I(t_2) = \frac{4.7 \, V}{10 \, \Omega} = 0.47 \, A;\] and \[I(t_3) = \frac{0.040 \, V}{10 \, \Omega} = 4.0 \times 10^{-3} \, A.\]

Significance

An emf voltage is created by a changing magnetic flux over time. If we know how the magnetic field varies with time over a constant area, we can take its time derivative to calculate the induced emf.

Example \(\PageIndex{1B}\): Changing Magnetic Field Inside a Solenoid

The current through the windings of a solenoid with \(n = 2000\) turns per meter is changing at a rate \(dI/dt = 3.0 \, A/s\). (See Sources of Magnetic Fields for a discussion of solenoids.) The solenoid is 50-cm long and has a cross-sectional diameter of 3.0 cm. A small coil consisting of \(N = 20\) closely wound turns wrapped in a circle of diameter 1.0 cm is placed in the middle of the solenoid such that the plane of the coil is perpendicular to the central axis of the solenoid. Assuming that the infinite-solenoid approximation is valid at the location of the small coil, determine the magnitude of the emf induced in the coil.

Strategy

The magnetic field in the middle of the solenoid is a uniform value of \(\mu_0 nI\). This field is producing a maximum magnetic flux through the coil as it is directed along the length of the solenoid. Therefore, the magnetic flux through the coil is the product of the solenoid’s magnetic field times the area of the coil. Faraday’s law involves a time derivative of the magnetic flux. The only quantity varying in time is the current, the rest can be pulled out of the time derivative. Lastly, we include the number of turns in the coil to determine the induced emf in the coil.

Solution

Since the field of the solenoid is given by \(B = \mu_0 nI\), the flux through each turn of the small coil is \[\Phi_m = \mu_0 nI\left(\frac{\pi d^2}{4}\right),\]

where d is the diameter of the coil. Now from Faraday’s law, the magnitude of the emf induced in the coil is

\[\epsilon = \left|N\frac{d\Phi_m}{dt}\right| = \left|N\mu_0 n\frac{\pi d^2}{4} \frac{dI}{dt}\right|\]

\[= 20 (4\pi \times 10^{-7} T \cdot m/s)(2000 \, m^{-1}) \frac{\pi(0.010 \, m)^2}{4} (3.0 \, A/s)\]\[= 1.2 \times 10^{-5} \, V.\]

Significance

When the current is turned on in a vertical solenoid, as shown in Figure \(\PageIndex{4}\), the ring has an induced emf from the solenoid’s changing magnetic flux that opposes the change. The result is that the ring is fired vertically into the air.

Figure \(\PageIndex{4}\): The jumping ring. When a current is turned on in the vertical solenoid, a current is induced in the metal ring. The stray field produced by the solenoid causes the ring to jump off the solenoid.

Note

A demonstration of the jumping ring from MIT.