12.7: Solenóides e toroides
- Page ID
- 184553
Ao final desta seção, você poderá:
- Estabeleça uma relação de como o campo magnético de um solenóide varia com a distância e a corrente usando a lei de Biot-Savart e a lei de Ampère
- Estabeleça uma relação de como o campo magnético de um toróide varia com a distância e a corrente usando a lei de Ampère
Dois dos dispositivos eletromagnéticos mais comuns e úteis são chamados de solenóides e toróides. De uma forma ou de outra, eles fazem parte de vários instrumentos, grandes e pequenos. Nesta seção, examinamos o campo magnético típico desses dispositivos.
Solenóides
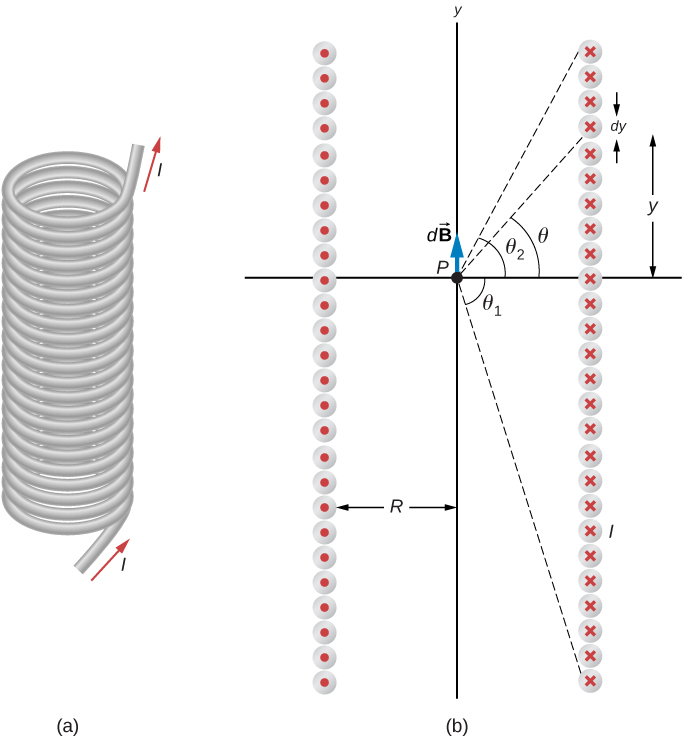
Um fio longo enrolado na forma de uma bobina helicoidal é conhecido como solenóide. Os solenóides são comumente usados em pesquisas experimentais que requerem campos magnéticos. Um solenóide geralmente é fácil de enrolar e, próximo ao seu centro, seu campo magnético é bastante uniforme e diretamente proporcional à corrente no fio.
A figura\(\PageIndex{1}\) mostra um solenóide que consiste em N voltas de fio firmemente enroladas em um comprimento L. Uma corrente I está fluindo ao longo do fio do solenóide. O número de voltas por unidade de comprimento é N/L; portanto, o número de voltas em um comprimento infinitesimal dy são (N/ L) voltas dy. Isso produz uma corrente
\[dI = \frac{NI}{L} dy. \label{12.24}\]
Primeiro calculamos o campo magnético no ponto P da Figura\(\PageIndex{1}\). Este ponto está no eixo central do solenóide. Estamos basicamente cortando o solenóide em fatias finas de espessura seca e tratando cada uma como um laço de corrente. Assim, dI é a corrente em cada fatia. O campo magnético\(d\vec{B}\) devido à corrente dI em dy pode ser encontrado com a ajuda da Equação 12.5.3 e da Equação\ ref {12.24}:
\[d\vec{B} = \frac{\mu_0 R^2 dI}{2(y^2 + R^2)^{3/2}}\hat{j} = \left( \frac{\mu_0 IR^2 N}{2L}\hat{j}\right) \frac{dy}{(y^2 + R^2)^{3/2}} \label{12.25}\]
onde usamos a Equação\ ref {12.24} para substituir dI. O campo resultante em P é encontrado pela integração\(d\vec{B}\) ao longo de todo o comprimento do solenóide. É mais fácil avaliar essa integral alterando a variável independente de y para\(\theta\). A partir da inspeção da Figura\(\PageIndex{1}\), temos:
\[sin \, \theta = \frac{y}{\sqrt{y^2 + R^2}}.\label{12.26}\]
Tomando o diferencial de ambos os lados dessa equação, obtemos
\[cos \, \theta \, d\theta = \left[ - \frac{y^2}{(y^2 + R^2)^{3/2}} + \frac{1}{\sqrt{y^2 + R^2}}\right] dy \]
\[ = \frac{R^2 dy}{(y^2 + R^2)^{3/2}}.\]
Quando isso é substituído na equação por\(d\vec{B}\), temos
\[\vec{B} = \frac{\mu_0 I N}{2L}\hat{j} \int_{\theta_1}^{\theta_2} cos \, \theta \, d\theta = \frac{\mu_0 I N}{2L} (sin \, \theta_2 - sin \, \theta_1)\hat{j}, \label{12.27}\]
que é o campo magnético ao longo do eixo central de um solenóide finito.
De especial interesse é o solenóide infinitamente longo, para o qual\(L \rightarrow \infty\). Do ponto de vista prático, o solenóide infinito é aquele cujo comprimento é muito maior que seu raio\((L >> R)\). Nesse caso,\(\theta_1 = \frac{-\pi}{2}\)\(\theta_2 = \frac{\pi}{2}\) e. Então, da Equação\ ref {12.27}, o campo magnético ao longo do eixo central de um solenóide infinito é
\[\vec{B} = \frac{\mu_0 IN}{2L} \hat{j} [sin(\pi/2) - sin(-\pi/2)] = \frac{\mu_0 IN}{L} \hat{j}\]ou
\[\vec{B} = \mu_0 n I \hat{j}, \label{12.28}\]
onde n é o número de voltas por unidade de comprimento. Você pode encontrar a direção de\(\vec{B}\) com uma regra da mão direita: enrole os dedos na direção da corrente e o polegar aponta ao longo do campo magnético no interior do solenóide.
Agora usamos essas propriedades, junto com a lei de Ampère, para calcular a magnitude do campo magnético em qualquer local dentro do solenóide infinito. Considere o caminho fechado da Figura\(\PageIndex{2}\). Ao longo do segmento 1,\(\vec{B}\) é uniforme e paralelo ao caminho. Ao longo dos segmentos 2 e 4,\(\vec{B}\) é perpendicular a parte do caminho e desaparece sobre o resto dele. Portanto, os segmentos 2 e 4 não contribuem para a integral da linha na lei de Ampère. Ao longo do segmento 3,\(\vec{B} = 0\) porque o campo magnético é zero fora do solenóide. Se você considerar um circuito da lei de Ampère fora do solenóide, a corrente flui em direções opostas em diferentes segmentos de fio. Portanto, não há corrente fechada nem campo magnético de acordo com a lei de Ampère. Portanto, não há contribuição para a integral de linha do segmento 3. Como resultado, encontramos
\[\oint \vec{B} \cdot d\vec{l} = \int_1 \vec{B} \cdot d\vec{l} = Bl. \label{12.29}\]
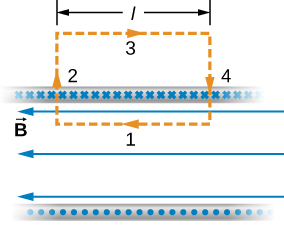
O solenóide tem n voltas por unidade de comprimento, então a corrente que passa pela superfície delimitada pelo caminho é NLi. Portanto, da lei de Ampère,
\[Bl = \mu_0 n lI\]e
\[B = \mu_0 n I \label{12.30}\]
dentro do solenóide. Isso concorda com o que encontramos anteriormente para B no eixo central do solenóide. Aqui, no entanto, a localização do segmento 1 é arbitrária, então descobrimos que essa equação fornece o campo magnético em todos os lugares dentro do solenóide infinito.
Fora do solenóide, pode-se desenhar um laço da lei de Ampère ao redor de todo o solenóide. Isso envolveria a corrente fluindo em ambas as direções. Portanto, a corrente líquida dentro do circuito é zero. De acordo com a lei de Ampère, se a corrente líquida for zero, o campo magnético deve ser zero. Portanto, para locais fora do raio do solenóide, o campo magnético é zero.
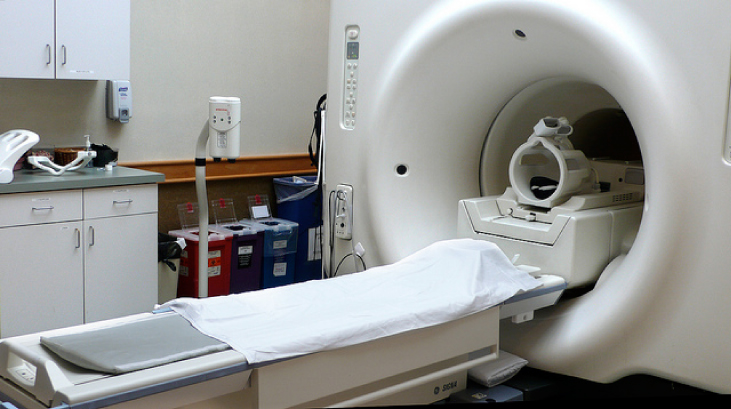
Quando um paciente é submetido a uma ressonância magnética (RM), a pessoa se deita em uma mesa que é movida para o centro de um grande solenóide que pode gerar campos magnéticos muito grandes. O solenóide é capaz desses campos altos a partir de altas correntes que fluem através de fios supercondutores. O grande campo magnético é usado para alterar o spin dos prótons no corpo do paciente. O tempo necessário para que os giros se alinhem ou relaxem (retornem à orientação original) é uma assinatura de diferentes tecidos que podem ser analisados para verificar se as estruturas dos tecidos estão normais (Figura\(\PageIndex{3}\)).
Um solenóide tem 300 voltas enroladas em torno de um cilindro de 1,20 cm de diâmetro e 14,0 cm de comprimento. Se a corrente através das bobinas for de 0,410 A, qual é a magnitude do campo magnético dentro e próximo ao meio do solenóide?
Estratégia
Recebemos o número de voltas e o comprimento do solenóide para que possamos encontrar o número de voltas por unidade de comprimento. Portanto, o campo magnético dentro e próximo ao meio do solenóide é dado pela Equação\ ref {12.30}. Fora do solenóide, o campo magnético é zero.
Solução
O número de voltas por unidade de comprimento é
\[n = \frac{300 \, turns}{0.140 \, m} = 2.14 \times 10^3 \, turns/m.\]
O campo magnético produzido dentro do solenóide é
\[B = \mu_0 nI = (4\pi \times 10^{-7} T \cdot m/A)(2.14 \times 10^3 turns/m)(0.410 \, A)\]
\[B = 1.10 \times 10^{-3}T.\]
Significância
Esta solução é válida somente se o comprimento do solenóide for razoavelmente grande em comparação com seu diâmetro. Este exemplo é um caso em que isso é válido.
Qual é a razão do campo magnético produzido pelo uso de uma fórmula finita sobre a aproximação infinita para um ângulo\(\theta\) de (a)\(85^o\)? (b)\(89^o\)? O solenóide tem 1000 voltas em 50 cm com uma corrente de 1,0 A fluindo pelas bobinas
- Solução
-
a. 1,00382; b. 1,00015
Toroides
Um toróide é uma bobina em forma de rosca enrolada estreitamente com um fio contínuo, conforme ilustrado na parte (a) da Figura\(\PageIndex{4}\). Se o toróide tem N enrolamentos e a corrente no fio é I, qual é o campo magnético dentro e fora do toróide?
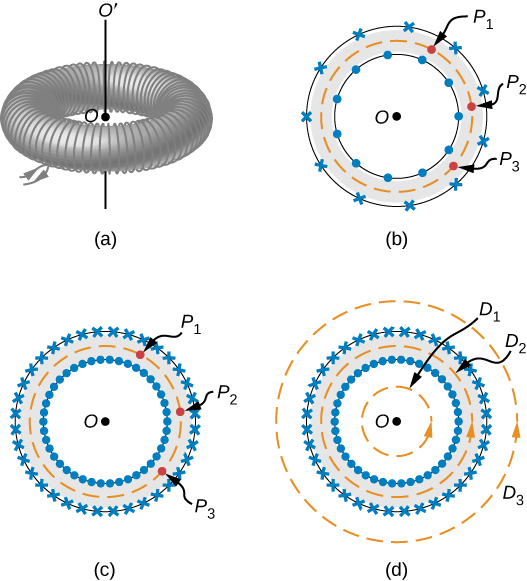
Começamos assumindo a simetria cilíndrica em torno do eixo OO '. Na verdade, essa suposição não está exatamente correta, pois, como\(\PageIndex{4}\) mostra a parte (b) da Figura, a visão da bobina toroidal varia de ponto a ponto (por exemplo,\(P_1, \, P_2\) e\(P_3\)) em um caminho circular centrado em torno de OO '. No entanto, se o toróide estiver bem enrolado, todos os pontos do círculo se tornarão essencialmente equivalentes [parte (c) da Figura\(\PageIndex{4}\)], e a simetria cilíndrica é uma aproximação precisa.
Com essa simetria, o campo magnético deve ser tangente e constante em magnitude ao longo de qualquer caminho circular centrado em OO '. Isso nos permite escrever para cada um dos caminhos\(D_1, \, D_2\) e\(D_3\) mostrados na parte (d) da Figura\(\PageIndex{4}\),
\[\oint \vec{B} \cdot d\vec{l} = B(2\pi r). \label{12.31}\]
A lei de Ampère relaciona essa integral com a corrente líquida que passa por qualquer superfície delimitada pelo caminho da integração. Para um caminho externo ao toróide, ou nenhuma corrente passa pela superfície envolvente (caminho\(D_1\)), ou a corrente que passa pela superfície em uma direção é exatamente equilibrada pela corrente que passa por ela na direção oposta (caminho\(D_3\)). Em ambos os casos, não há corrente líquida passando pela superfície, então
\[\oint B(2\pi r) = 0\]e
\[B = 0 \, (outside \, the \, toroid). \label{12.32}\]
As curvas de um toróide formam uma hélice, em vez de laços circulares. Como resultado, há um pequeno campo externo à bobina; no entanto, a derivação acima é válida se as bobinas forem circulares.
Para um caminho circular dentro do toróide (caminho\(D_2\)), a corrente no fio corta a superfície N vezes, resultando em uma corrente líquida NI através da superfície. Agora descobrimos com a lei de Ampère,
\[B(2\pi r) = \mu_0 NI\]e
\[B = \frac{\mu_0 NI}{2\pi r} \, (within \, the \, toroid). \label{12.33}\]
O campo magnético é direcionado no sentido anti-horário para os enrolamentos mostrados. Quando a corrente nas bobinas é invertida, a direção do campo magnético também se inverte.
O campo magnético dentro de um toróide não é uniforme, pois varia inversamente com a distância r do eixo OO '. No entanto, se o raio central R (o raio intermediário entre os raios interno e externo do toróide) for muito maior que o diâmetro da seção transversal das bobinas r, a variação é relativamente pequena e a magnitude do campo magnético pode ser calculada pela Equação\ ref {12.33} onde \(r = R\).


