12.5: Campo magnético de um circuito de corrente
- Page ID
- 184551
Ao final desta seção, você poderá:
- Explique como a lei de Biot-Savart é usada para determinar o campo magnético devido a uma corrente em um laço de fio em um ponto ao longo de uma linha perpendicular ao plano do circuito.
- Determine o campo magnético de um arco de corrente.
O circuito circular da Figura\(\PageIndex{1}\) tem um raio R, carrega uma corrente I e está no plano xz. Qual é o campo magnético devido à corrente em um ponto arbitrário P ao longo do eixo do circuito?
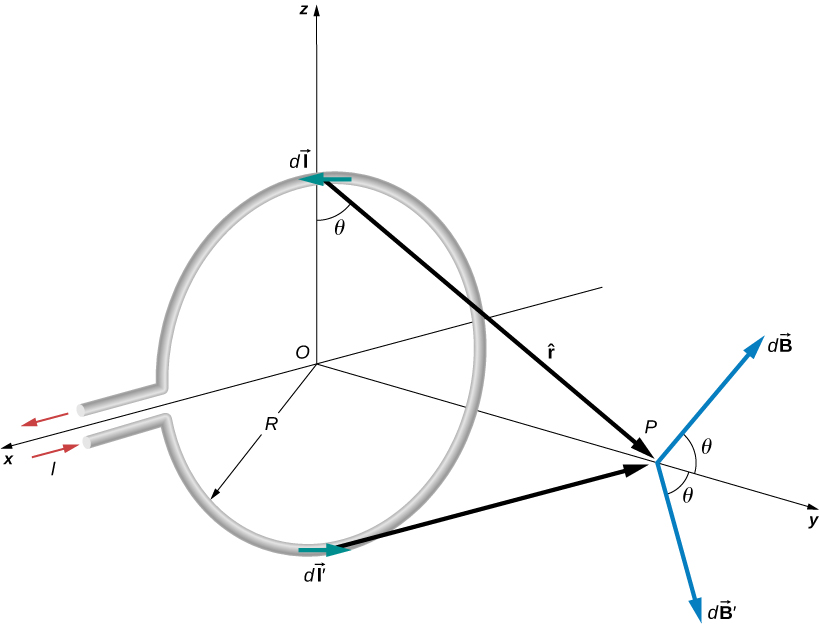
Podemos usar a lei de Biot-Savart para encontrar o campo magnético devido a uma corrente. Primeiro, consideramos segmentos arbitrários em lados opostos do loop para mostrar qualitativamente pelos resultados vetoriais que a direção do campo magnético líquido está ao longo do eixo central do loop. A partir daí, podemos usar a lei de Biot-Savart para derivar a expressão do campo magnético.
Seja P a uma distância y do centro do loop. A partir da regra da direita, o campo magnético\(d\vec{B}\) em P, produzido pelo elemento atual,\(I \, d\vec{l}\) é direcionado em um ângulo\(\theta\) acima do eixo y, conforme mostrado. Como\(d\vec{l}\) é paralelo ao longo do eixo x e\(\hat{r}\) está no plano yz, os dois vetores são perpendiculares, então temos
\[dB = \frac{\mu_0}{4\pi} \frac{I \, dl \, sin \, \pi/2}{r^2} = \frac{\mu_0}{4\pi} \frac{I \, dl}{y^2 + R^2} \label{12.13}\]onde temos usado\(r^2 = y^2 + R^2\).
Agora, considere o campo magnético\(d\vec{B}'\) devido ao elemento atual\(I \, d\vec{l}'\), que é diretamente oposto ao\(I \, d\vec{l}\) loop. A magnitude de também\(d\vec{B}'\) é dada pela Equação\ ref {12.13}, mas é direcionada a um ângulo θ abaixo do eixo y. Os componentes\(d\vec{B}\) e\(d\vec{B}'\) perpendiculares ao eixo y, portanto, cancelam e, ao calcular o campo magnético líquido, somente os componentes ao longo do eixo y precisam ser considerados. Os componentes perpendiculares ao eixo do loop somam zero em pares. Portanto, no ponto P:
\[\vec{B} = \hat{j} \int_{loop} dB \, cos \, \theta = \hat{j} \frac{\mu_0 I}{4\pi} \int_{loop}\frac{cos \, \theta \, dl}{y^2 + R^2}. \label{12.14}\]
Para todos os elementos\(d\vec{l}\) do fio, y, R e\(\theta\) são constantes e estão relacionados por
\[cos \, \theta = \frac{R}{\sqrt{y^2 + R^2}}. \nonumber\]
Agora, da Equação\ ref {12.14}, o campo magnético em P é
\[\vec{B} = \hat{j}\frac{\mu_0IR}{4\pi (y^2 + R^2)^{3/2}} \int_{loop}dl = \frac{\mu_0 IR^2}{2(y^2 + R^2)^{3/2}}\hat{j} \label{12.15}\]onde temos usado\(\int_{loop}dl = 2\pi R\). Conforme discutido no capítulo anterior, o circuito fechado de corrente é um dipolo magnético do momento\(\vec{\mu} = I \, A\hat{n}\). Para este exemplo,\(A = \pi R^2\) e\(\hat{n} = \hat{j}\), portanto, o campo magnético em P também pode ser escrito como
\[\vec{B} = \frac{\mu_0 \mu \hat{j}}{2\pi (y^2 + R^2)^{3/2}}. \label{12.16}\]
Ao definir\(y = 0\) na Equação\ ref {12.16}, obtemos o campo magnético no centro do loop:
\[\vec{B} = \frac{\mu_0 I}{2R} \hat{j} \label{12.17}.\]
Essa equação se torna\(B = \mu_0 n I/(2R)\) para uma bobina plana de n laços por comprimento. Também pode ser expresso como
\[\vec{B} = \frac{\mu_0\vec{\mu}}{2\pi R^3}. \label{12.18}\]
Se considerarmos\(y >> R\) na Equação\ ref {12.16}, a expressão se reduz a uma expressão conhecida como campo magnético de um dipolo:
\[\vec{B} = \frac{\mu_0 \vec{\mu}}{2\pi y^3}. \label{12.19}\]
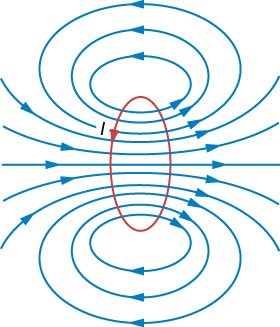
O cálculo do campo magnético devido ao circuito de corrente circular em pontos fora do eixo requer matemática bastante complexa, então veremos os resultados. As linhas do campo magnético são moldadas conforme mostrado na Figura\(\PageIndex{2}\). Observe que uma linha de campo segue o eixo do loop. Esta é a linha de campo que acabamos de encontrar. Além disso, bem próximas ao fio, as linhas de campo são quase circulares, como as linhas de um fio longo e reto.
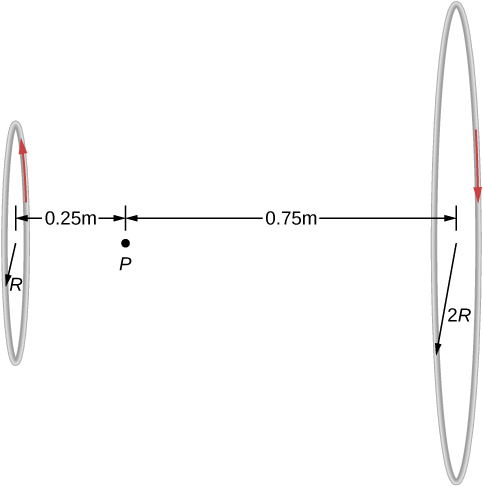
Dois laços de fio transportam a mesma corrente de 10 mA, mas fluem em direções opostas, como visto na Figura\(\PageIndex{3}\). Um loop é medido para ter um raio de,\(R = 50 \, cm\) enquanto o outro loop tem um raio de\(2R = 100 \, cm\). A distância do primeiro loop até o ponto em que o campo magnético é medido é de 0,25 m, e a distância desse ponto até o segundo loop é de 0,75 m. Qual é a magnitude do campo magnético líquido no ponto P?
Estratégia
O campo magnético no ponto P foi determinado na Equação\ ref {12.15}. Como as correntes estão fluindo em direções opostas, o campo magnético líquido é a diferença entre os dois campos gerados pelas bobinas. Usando as quantidades fornecidas no problema, o campo magnético líquido é então calculado.
Solução
Resolver o campo magnético líquido usando a Equação\ ref {12.15} e as quantidades dadas no problema produz
\[B = \frac{\mu_0 IR_1^2}{2(y_1^2 + R_1^2)^{3/2}} - \frac{\mu_0 IR_2^2}{2(y_2^2 + R_2^2)^{3/2}}\]
\[B = \frac{(4\pi \times 10^{-7}T \cdot m/A)(0.010 \, A)(0.5 \, m)^2}{2((0.25 \, m)^2 + (0.5 \, m)^2)^{3/2}} - \frac{(4\pi \times 10^{-7}T \cdot m/A)(0.010 \, A)(1.0 \, m)^2}{2((0.75 \, m)^2 + (1.0 \, m)^2)^{3/2}}\]
\(B = 5.77 \times 10^{-9}T\)para a direita.
Significância
As bobinas Helmholtz normalmente têm laços com raios iguais, com corrente fluindo na mesma direção para ter um campo forte e uniforme no ponto médio entre os laços. Uma aplicação similar da distribuição do campo magnético criada pelas bobinas de Helmholtz é encontrada em uma garrafa magnética que pode capturar temporariamente partículas carregadas. Veja Magnetic Forces and Fields para uma discussão sobre isso.
Usando o exemplo\(\PageIndex{1}\), a que distância você teria que mover a primeira bobina para ter zero campo magnético mensurável no ponto P?
- Solução
-
0.608 metros


