11.4: Movimento de uma partícula carregada em um campo magnético

Objetivos de

Ao final desta seção, você poderá:

• Explicar como uma partícula carregada em um campo magnético externo sofre movimento circular
• Descreva como determinar o raio do movimento circular de uma partícula carregada em um campo magnético

Uma partícula carregada experimenta uma força ao se mover através de um campo magnético. O que acontece se esse campo for uniforme sobre o movimento da partícula carregada? Qual caminho a partícula segue? Nesta seção, discutimos o movimento circular da partícula carregada, bem como outros movimentos que resultam da entrada de uma partícula carregada em um campo magnético.

O caso mais simples ocorre quando uma partícula carregada se move perpendicularmente a um campo B uniforme (Figura\(\PageIndex{1}\)). Se o campo estiver no vácuo, o campo magnético é o fator dominante que determina o movimento. Como a força magnética é perpendicular à direção da viagem, uma partícula carregada segue um caminho curvo em um campo magnético. A partícula continua seguindo esse caminho curvo até formar um círculo completo. Outra forma de ver isso é que a força magnética é sempre perpendicular à velocidade, de modo que não funciona na partícula carregada. A energia cinética e a velocidade da partícula, portanto, permanecem constantes. A direção do movimento é afetada, mas não a velocidade.

Figura\(\PageIndex{1}\): Uma partícula carregada negativamente se move no plano do papel em uma região onde o campo magnético é perpendicular ao papel (representado pelas pequenas\(X\) — como as pontas das flechas). A força magnética é perpendicular à velocidade, então a velocidade muda na direção, mas não na magnitude. O resultado é um movimento circular uniforme. (Observe que, como a carga é negativa, a força é oposta à previsão da regra da mão direita.)

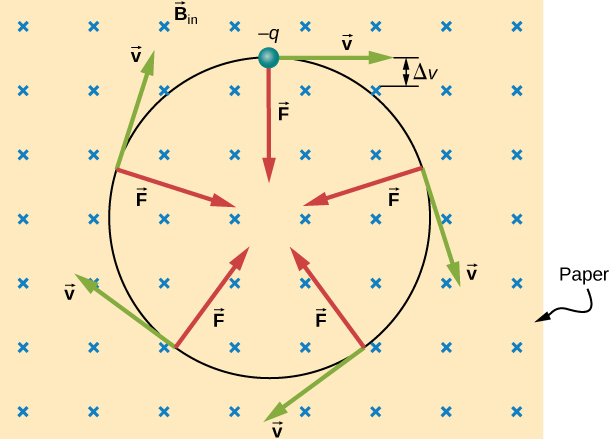
Nessa situação, a força magnética fornece a força centrípeta\(F_C = \dfrac{mv^2}{r}\). Observando que a velocidade é perpendicular ao campo magnético, a magnitude da força magnética é reduzida para\(F = qvB\). Como a força magnética F fornece a força centrípeta\(F_C\), temos

\[qvB = \dfrac{mv^2}{r}.\]

Resolvendo para r rendimentos

\[r = \dfrac{mv}{qB}. \label{11.5}\]

Aqui, r é o raio de curvatura do caminho de uma partícula carregada com massa m e carga q, movendo-se a uma velocidade v que é perpendicular a um campo magnético de força B. O tempo para a partícula carregada contornar o caminho circular é definido como o período, que é o mesmo que a distância percorrida (a circunferência) dividida pela velocidade. Com base nisso e na equação, podemos derivar o período de movimento como

\[T = \dfrac{2\pi r}{v} = \dfrac{2\pi}{v} \dfrac{mv}{qB} = \dfrac{2\pi m}{qB}. \label{11.6}\]

Se a velocidade não for perpendicular ao campo magnético, podemos comparar cada componente da velocidade separadamente com o campo magnético. O componente da velocidade perpendicular ao campo magnético produz uma força magnética perpendicular a essa velocidade e ao campo:

\[\begin{align} v_{perp} &= v \, \sin \theta \\[4pt] v_{para} &= v \, \cos \theta. \end{align}\]

onde\(\theta\) está o ângulo entre v e B. O componente paralelo ao campo magnético cria um movimento constante na mesma direção do campo magnético, também mostrado na Equação. O movimento paralelo determina o tom p da hélice, que é a distância entre as curvas adjacentes. Essa distância é igual ao componente paralelo da velocidade vezes o período:

\[p = v_{para} T. \label{11.8}\]

O resultado é um movimento helicoidal, conforme mostrado na figura a seguir.

Figura\(\PageIndex{2}\): Uma partícula carregada se movendo com uma velocidade que não está na mesma direção do campo magnético. O componente de velocidade perpendicular ao campo magnético cria movimento circular, enquanto o componente da velocidade paralelo ao campo move a partícula ao longo de uma linha reta. O tom é a distância horizontal entre dois círculos consecutivos. O movimento resultante é helicoidal.

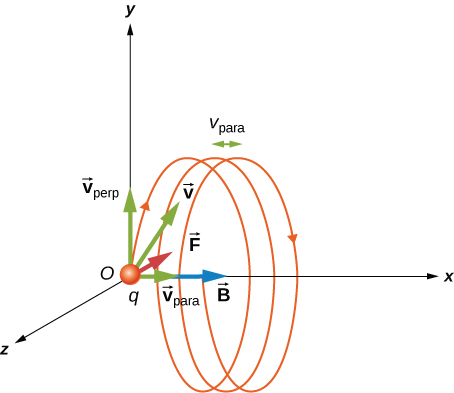
Enquanto a partícula carregada viaja em um caminho helicoidal, ela pode entrar em uma região onde o campo magnético não é uniforme. Em particular, suponha que uma partícula viaje de uma região de campo magnético forte para uma região de campo mais fraco, depois de volta para uma região de campo mais forte. A partícula pode refletir de volta antes de entrar na região mais forte do campo magnético. Isso é semelhante a uma onda em uma corda viajando de uma corda muito leve e fina para uma parede dura e refletindo para trás. Se a reflexão ocorrer nas duas extremidades, a partícula fica presa na chamada garrafa magnética.

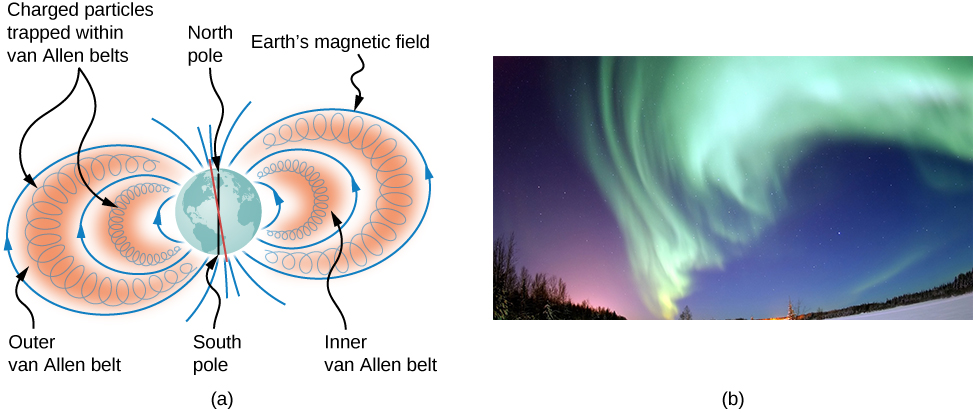
Partículas presas em campos magnéticos são encontradas nos cinturões de radiação de Van Allen ao redor da Terra, que fazem parte do campo magnético da Terra. Esses cinturões foram descobertos por James Van Allen ao tentar medir o fluxo de raios cósmicos na Terra (partículas de alta energia que vêm de fora do sistema solar) para ver se isso era semelhante ao fluxo medido na Terra. Van Allen descobriu que, devido à contribuição de partículas presas no campo magnético da Terra, o fluxo era muito maior na Terra do que no espaço sideral. As auroras, como a famosa aurora boreal (aurora boreal) no hemisfério norte (Figura\(\PageIndex{3}\)), são belas exibições de luz emitida à medida que os íons se recombinam com os elétrons que entram na atmosfera à medida que espiralam ao longo das linhas do campo magnético. (Os íons são principalmente átomos de oxigênio e nitrogênio que são inicialmente ionizados por colisões com partículas energéticas na atmosfera da Terra.) Auroras também foram observadas em outros planetas, como Júpiter e Saturno.

Figura\(\PageIndex{3}\): (a) Os cinturões de radiação de Van Allen ao redor da Terra capturam íons produzidos pelos raios cósmicos que atingem a atmosfera da Terra. (b) O magnífico espetáculo da aurora boreal, ou aurora boreal, brilha no céu do norte acima do Lago Bear, perto da Base da Força Aérea de Eielson, Alasca. Moldada pelo campo magnético da Terra, essa luz é produzida por moléculas brilhantes e íons de oxigênio e nitrogênio. (crédito b: modificação do trabalho do aviador sênior da USAF Joshua Strang)

Exemplo\(\PageIndex{1}\): Beam Deflector

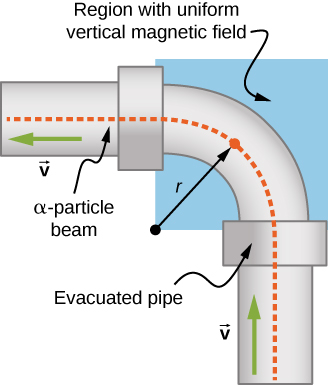
Um grupo de pesquisa está investigando isótopos radioativos de curta duração. Eles precisam projetar uma forma de transportar partículas alfa (núcleos de hélio) de onde são feitas para um local onde colidirão com outro material para formar um isótopo. O feixe de partículas alfa\( (m = 6.64 \times 10^{-27}kg, \, q = 3.2 \times 10^{-19}C)\) se curva através de uma região de 90 graus com um campo magnético uniforme de 0,050 T (Figura\(\PageIndex{4}\)). (a) Em que direção o campo magnético deve ser aplicado? (b) Quanto tempo as partículas alfa levam para atravessar a região uniforme do campo magnético?

Figura\(\PageIndex{4}\): Vista superior da configuração do defletor de feixe.

Estratégia

1. A direção do campo magnético é mostrada pelo RHR-1. Seus dedos apontam na direção de v, e seu polegar precisa apontar na direção da força, para a esquerda. Portanto, como as partículas alfa estão carregadas positivamente, o campo magnético deve apontar para baixo.
2. O período em que a partícula alfa contorna o círculo é

\[T = \dfrac{2\pi m}{qB}.\]

Como a partícula está girando apenas em torno de um quarto de círculo, podemos usar 0,25 vezes o período para encontrar o tempo necessário para contornar esse caminho.

Solução

1. Vamos começar focando na partícula alfa que entra no campo próximo à parte inferior da imagem. Primeiro, aponte o polegar para cima na página. Para que a palma da mão se abra para a esquerda, onde a força centrípeta (e, portanto, a força magnética) aponta, seus dedos precisam mudar de orientação até apontarem para a página. Essa é a direção do campo magnético aplicado.
2. O período em que a partícula carregada gira em torno de um círculo é calculado usando a massa, a carga e o campo magnético fornecidos no problema. \[T = \dfrac{2\pi m}{qB} = \dfrac{2\pi (6.64 \times 10^{-27}kg)}{(3.2 \times 10^{-19}C)(0.050 \, T)} = 2.6 \times 10^{-6}s.\]No entanto, para o problema dado, a partícula alfa gira em torno de um quarto do círculo, então o tempo necessário seria\[t = 0.25 \times 2.61 \times 10^{-6}s = 6.5 \times 10^{-7}s.\]

Significância

Esse tempo pode ser rápido o suficiente para chegar ao material que gostaríamos de bombardear, dependendo de quão curta o isótopo radioativo tem e continua emitindo partículas alfa. Se pudéssemos aumentar o campo magnético aplicado na região, isso encurtaria ainda mais o tempo. O caminho que as partículas precisam seguir pode ser reduzido, mas isso pode não ser econômico, dada a configuração experimental.

Exercício\(\PageIndex{1}\)

Um campo magnético uniforme de magnitude 1,5 T é direcionado horizontalmente de oeste para leste. (a) Qual é a força magnética em um próton no instante em que ele está se movendo verticalmente para baixo no campo com uma velocidade de\(4 \times 10^7 \, m/s\)? (b) Compare essa força com o peso w de um próton.

Solução

a.\(9.6 \times 10^{-12}N\) em direção ao sul;

b.\(\dfrac{w}{F_m} = 1.7 \times 10^{-15}\)

Exemplo\(\PageIndex{2}\): Helical Motion in a Magnetic Field

Um próton entra em um campo magnético uniforme de\(1.0 \times 10^{-4}T\) com uma velocidade de\(5 \times 10^5 \, m/s\). Em que ângulo o campo magnético deve estar a partir da velocidade para que o tom do movimento helicoidal resultante seja igual ao raio da hélice?

Estratégia

O tom do movimento está relacionado à velocidade paralela vezes o período do movimento circular, enquanto o raio se relaciona com o componente de velocidade perpendicular. Depois de definir o raio e o tom iguais um ao outro, resolva o ângulo entre o campo magnético e a velocidade ou\(\theta\).

Solução

O tom é dado pela Equação\ ref {11.8}, o período é dado pela Equação\ ref {11.6} e o raio do movimento circular é dado pela Equação\ ref {11.5}. Observe que a velocidade na equação do raio está relacionada somente à velocidade perpendicular, que é onde o movimento circular ocorre. Portanto, substituímos o componente senoidal da velocidade geral na equação do raio para igualar o tom e o raio

\[p = r\]

\[v_{\parallel}T = \dfrac{mv}{qB}\]

\[v \, cos \, \theta \dfrac{2\pi m}{qB} = \dfrac{mv \, sin \, \theta}{qB}\]

\[2\pi = tan \, \theta\]

\[\theta = 81.0^o.\]

Significância

Se esse ângulo fosse\(0^o\), somente a velocidade paralela ocorreria e a hélice não se formaria, porque não haveria movimento circular no plano perpendicular. Se esse ângulo fosse\(90^o\) apenas um movimento circular ocorreria e não haveria movimento dos círculos perpendiculares ao movimento. É isso que cria o movimento helicoidal.