11.3: Campos e linhas magnéticas
- Page ID
- 184803
Ao final desta seção, você poderá:
- Defina o campo magnético com base em uma carga em movimento que sofre uma força
- Aplique a regra da mão direita para determinar a direção de uma força magnética com base no movimento de uma carga em um campo magnético
- Desenhe linhas de campo magnético para entender para que lado o campo magnético aponta e quão forte ele é em uma região do espaço
Descrevemos as propriedades dos ímãs, descrevemos como eles se comportam e listamos algumas das aplicações das propriedades magnéticas. Mesmo que não existam cargas magnéticas isoladas, ainda podemos definir a atração e a repulsão de ímãs com base em um campo. Nesta seção, definimos o campo magnético, determinamos sua direção com base na regra da mão direita e discutimos como desenhar linhas de campo magnético.
Definindo o campo magnético
Um campo magnético é definido pela força que uma partícula carregada experimenta se movendo nesse campo, depois de contabilizarmos as forças gravitacionais e quaisquer forças elétricas adicionais possíveis na carga. A magnitude dessa força é proporcional à quantidade de carga q, à velocidade da partícula carregada v e à magnitude do campo magnético aplicado. A direção dessa força é perpendicular à direção da partícula carregada em movimento e à direção do campo magnético aplicado. Com base nessas observações, definimos a intensidade do campo magnético B com base na força magnética\(\vec{F}\) em uma carga q se movendo em velocidade como o produto cruzado da velocidade e do campo magnético, ou seja,
\[\vec{F} = q\vec{v} \times \vec{B}. \label{eq1}\]
Na verdade, é assim que definimos o campo magnético\(\vec{B}\) - em termos da força sobre uma partícula carregada que se move em um campo magnético. A magnitude da força é determinada a partir da definição do produto cruzado no que se refere às magnitudes de cada um dos vetores. Em outras palavras, a magnitude da força satisfaz
\[F = qv \, B \sin \, \theta \label{eq2}\]
onde θ é o ângulo entre a velocidade e o campo magnético.
A unidade SI para intensidade do campo magnético\(B\) é chamada de tesla (T) em homenagem ao excêntrico, mas brilhante inventor Nikola Tesla (1856-1943), onde
\[1 \, T = \frac{1 \, N}{A \cdot m}.\]
Às vezes, uma unidade menor, chamada gauss (G), é usada, onde
\[1 \, G = 10^{-4} \,T\]
Os ímãs permanentes mais fortes têm campos próximos a 2 T; eletroímãs supercondutores podem atingir 10 T ou mais. O campo magnético da Terra em sua superfície é apenas cerca de\(5 \times 10^{-5}\, T\) ou\(0.5 \,G\).
A direção da força magnética\(\vec{F}\) é perpendicular ao plano formado por\(\vec{v}\) e\(\vec{B}\) conforme determinado pela regra do lado direito-1 (ou RHR-1), ilustrada na Figura\(\PageIndex{1}\).
- Oriente sua mão direita para que seus dedos se curvem no plano definido pelos vetores de velocidade e campo magnético.
- Usando a mão direita, passe da velocidade em direção ao campo magnético com os dedos pelo menor ângulo possível.
- A força magnética é direcionada para onde seu polegar está apontando.
- Se a carga for negativa, inverta a direção encontrada por essas etapas.
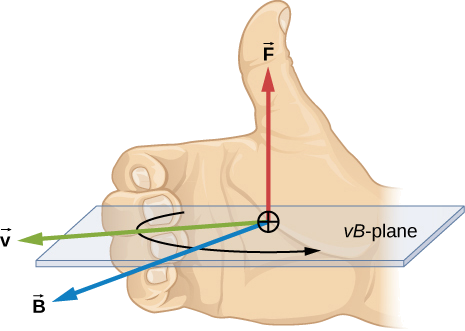
Figura\(\PageIndex{1}\): Os campos magnéticos exercem forças sobre cargas em movimento. A direção da força magnética em uma carga em movimento é perpendicular ao plano formado por b\(\vec{v}\)\(\vec{B}\) e segue a regra do lado direito-1 (RHR-1), conforme mostrado. A magnitude da força é proporcional ao\(q, \, v, \, B,\) seno do ângulo entre\(\vec{v}\)\(\vec{B}\) e.
Visite este site para obter práticas adicionais com a direção dos campos magnéticos.
Não há força magnética nas cargas estáticas. No entanto, há uma força magnética nas cargas que se movem em ângulo com um campo magnético. Quando as cargas estão estacionárias, seus campos elétricos não afetam os ímãs. No entanto, quando as cargas se movem, elas produzem campos magnéticos que exercem forças sobre outros ímãs. Quando há movimento relativo, surge uma conexão entre forças elétricas e magnéticas - uma afeta a outra.
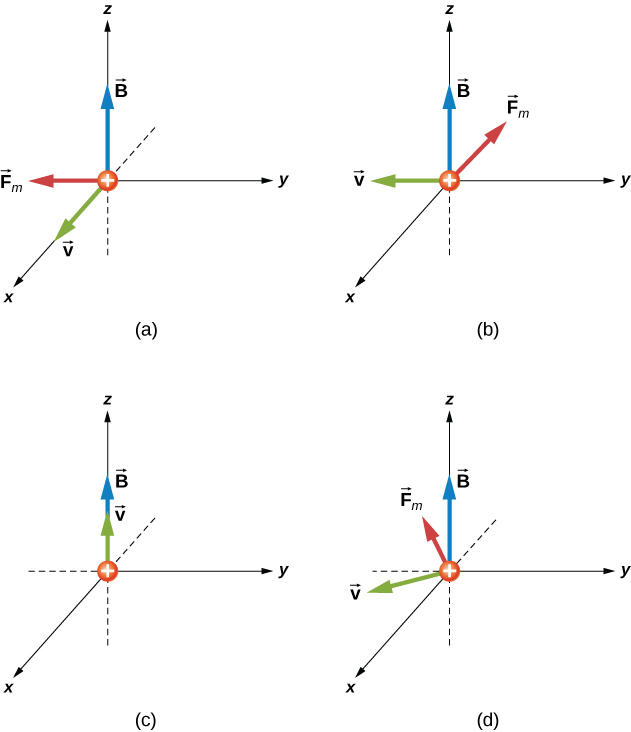
Uma partícula alfa\((q = 3.2 \times 10^{-19}C)\) se move através de um campo magnético uniforme cuja magnitude é 1,5 T. O campo é diretamente paralelo ao eixo z positivo do sistema de coordenadas retangulares da Figura\(\PageIndex{2}\). Qual é a força magnética na partícula alfa quando ela está se movendo (a) na direção x positiva com uma velocidade de\(5.0 \times 10^4 m/s\)? (b) na direção y negativa com uma velocidade de\(5.0 \times 10^4 m/s\)? (c) na direção z positiva com uma velocidade de\(5.0 \times 10^4 m/s\)? (d) com uma velocidade\(\vec{v} = \left(2.0 \hat{i} - 3.0 \hat{j} + 1.0 \hat{k} \right) \times 10^4 m/s\)?
Estratégia
Recebemos a carga, sua velocidade e a força e direção do campo magnético. Assim, podemos usar a equação\(\vec{F} = q \vec{v} \times \vec{B}\) ou\(F = qv \, B sin\, \theta\) calcular a força. A direção da força é determinada pela RHR-1.
Solução
- Primeiro, para determinar a direção, comece com os dedos apontando na direção x positiva. Varra os dedos para cima na direção do campo magnético. Seu polegar deve apontar na direção y negativa. Isso deve corresponder à resposta matemática. Para calcular a força, usamos a carga, a velocidade e o campo magnético fornecidos e a definição da força magnética na forma de produto cruzado para calcular:\[\vec{F} = q\vec{v} \times \vec{B} = (3.2 \times 10^{-19} C) (5.0 \times 10^4 m/s \, \hat{i}) \times (1.5 \, T \, \hat{k}) = - 2.4 \times 10^{-14} N \, \hat{j}\]
- Primeiro, para determinar a direcionalidade, comece com os dedos apontando na direção y negativa. Varra os dedos para cima na direção do campo magnético, como no problema anterior. Seu polegar deve estar aberto na direção x negativa. Isso deve corresponder à resposta matemática. Para calcular a força, usamos a carga, a velocidade e o campo magnético fornecidos e a definição da força magnética na forma de produto cruzado para calcular:\[\vec{F} = q\vec{v} \times \vec{B} = (3.2 \times 10^{-19} C) (- 5.0 \times 10^4 m/s \, \hat{i}) \times (1.5 \, T \, \hat{k}) = - 2.4 \times 10^{-14} N \, \hat{i}\] Uma abordagem alternativa é usar a Equação\ ref {eq2} para encontrar a magnitude da força. Isso se aplica às partes (a) e (b). Como a velocidade é perpendicular ao campo magnético, o ângulo entre elas é de 90 graus. Portanto, a magnitude da força é:\[F = qv \, B \sin \, \theta = (3.2 \times 10^{-19} C)(5.0 \times 10^4m/s)(1.5 \, T) sin (90^o)) = 2.4 \times 10^{-14} N.\]
- Como a velocidade e o campo magnético são paralelos entre si, não há orientação de sua mão que resulte em uma direção de força. Portanto, a força nessa carga em movimento é zero. Isso é confirmado pelo produto cruzado. Quando você cruza dois vetores apontando na mesma direção, o resultado é igual a zero.
- Primeiro, para determinar a direção, seus dedos podem apontar em qualquer orientação; no entanto, você deve varrer os dedos para cima na direção do campo magnético. Ao girar a mão, observe que o polegar pode apontar em qualquer direção x ou y possível, mas não na direção z. Isso deve corresponder à resposta matemática. Para calcular a força, usamos a carga, a velocidade e o campo magnético fornecidos e a definição da força magnética na forma de produto cruzado para calcular:\[\vec{F} = q\vec{v} \times \vec{B} = (3.2 \times 10^{-19} C)((2.0 \hat{i} - 3.0 \hat{j} + 1.0 \hat{k}) \times 10^4 m/s) \times (1.5 \, T \hat{k})\]\[(-14.4 \hat{i} - 9.6 \hat{j}) \times 10^{-15}N.\] Esta solução pode ser reescrita em termos de magnitude e ângulo no plano xy:\[|\vec{F}| = \sqrt{F_x^2 + F_y^2} = \sqrt{(-14.4)^2 + (-9.6)^2} \times 10^{-15} N = 1.7 \times 10^{-14}N\]\[\theta = tan^{-1} \left(\frac{F_y}{F_x}\right) = tan^{-1} \left(\frac{-9.6 \times 10^{-15}N}{-14.4 \times 10^{-15}N} \right) = 34^o.\] A magnitude da força também pode ser calculada usando a Equação\ ref {eq2}. A velocidade nessa questão, no entanto, tem três componentes. O componente z da velocidade pode ser negligenciado, pois é paralelo ao campo magnético e, portanto, não gera força. A magnitude da velocidade é calculada a partir dos componentes x e y. O ângulo entre a velocidade no plano xy e o campo magnético no plano z é de 90 graus. Portanto, a força é calculada para ser:\[|\vec{v}| = \sqrt{(2)^2 + (-3)^2} \times 10^4 \frac{m}{s} = 3.6 \times 10^4 \frac{m}{s}\]\[F = qv \, Bsin \, \theta = (3.2 \times 10^{-19}C)(3.6 \times 10^4 m/s) (1.5 \, T) sin (90^o) = 1.7 \times 10^{-14} N\]
Significância
O produto cruzado nessa fórmula resulta em um terceiro vetor que deve ser perpendicular aos outros dois. Outras grandezas físicas, como o momento angular, também têm três vetores relacionados pelo produto cruzado. Observe que os valores de força típicos em problemas de força magnética são muito maiores do que a força gravitacional. Portanto, para uma carga isolada, a força magnética é a força dominante que rege o movimento da carga.
Repita o problema anterior com o campo magnético na direção x em vez de na direção z. Verifique suas respostas com o RHR-1.
- Responda a um
-
0 N
- Resposta b
-
\(2.4 \times 10^{-14}\hat{k} N\)
- Resposta c
-
\(2.4 \times 10^{-14}\hat{j} N\)
- Resposta d
-
\(7.2 \hat{j} + 2.2 \hat{k}) \times 10^{-15}N\)
Representando campos magnéticos
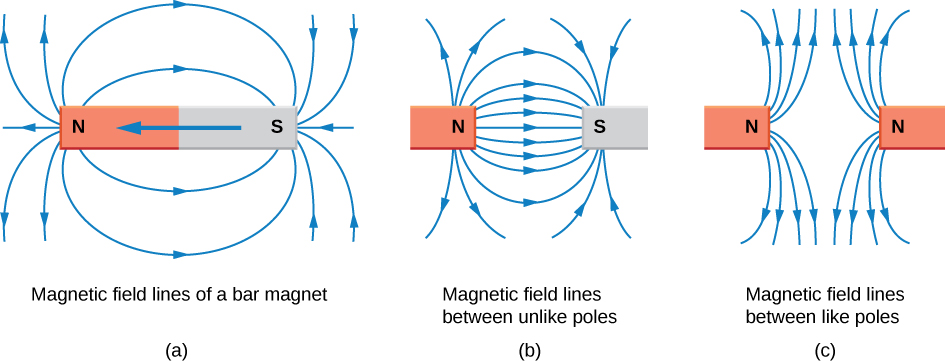
A representação de campos magnéticos por linhas de campo magnético é muito útil para visualizar a força e a direção do campo magnético. Conforme mostrado na Figura\(\PageIndex{3}\), cada uma dessas linhas forma um circuito fechado, mesmo que não seja mostrada pelas restrições do espaço disponível para a figura. As linhas de campo emergem do pólo norte (N), circulam até o pólo sul (S) e continuam pela barra magnética de volta ao pólo norte.
As linhas do campo magnético têm várias regras rígidas:
- A direção do campo magnético é tangente à linha do campo em qualquer ponto do espaço. Uma pequena bússola apontará na direção da linha do campo.
- A intensidade do campo é proporcional à proximidade das linhas. É exatamente proporcional ao número de linhas por unidade de área perpendicular às linhas (chamada densidade de área).
- As linhas do campo magnético nunca podem se cruzar, o que significa que o campo é único em qualquer ponto do espaço.
- As linhas do campo magnético são contínuas, formando ciclos fechados sem começo nem fim. Eles são direcionados do pólo norte para o pólo sul.
A última propriedade está relacionada ao fato de que os pólos norte e sul não podem ser separados. É uma diferença distinta das linhas de campo elétrico, que geralmente começam com cargas positivas e terminam com cargas negativas ou no infinito. Se existissem cargas magnéticas isoladas (chamadas de monopolos magnéticos), as linhas do campo magnético começariam e terminariam nelas.