Skip to main content
Global

8.5: Capacitor com um dielétrico

  1. Last updated
  2. Save as PDF
  • Page ID
    184626

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Descreva os efeitos que um dielétrico em um capacitor tem na capacitância e em outras propriedades
    • Calcule a capacitância de um capacitor contendo um dielétrico

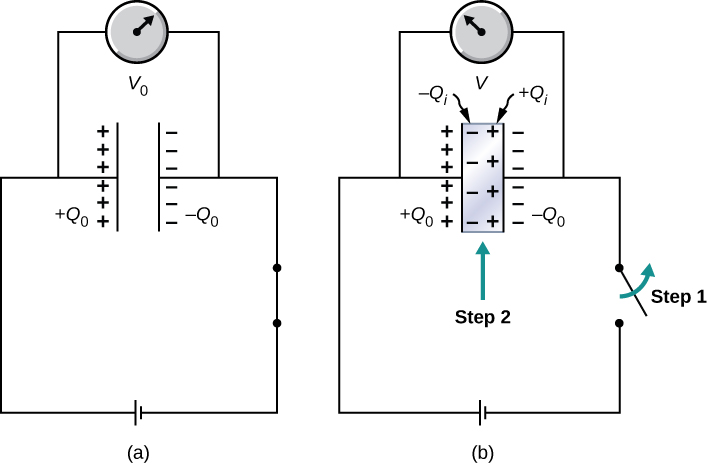
    Como discutimos anteriormente, um material isolante colocado entre as placas de um capacitor é chamado de dielétrico. A inserção de um dielétrico entre as placas de um capacitor afeta sua capacitância. Para ver o porquê, vamos considerar um experimento descrito na Figura\(\PageIndex{1}\). Inicialmente, um capacitor com capacitância\(C_0\) quando há ar entre suas placas é carregado por uma bateria até a voltagem\(V_0\). Quando o capacitor está totalmente carregado, a bateria é desconectada. Uma carga\(Q_0\) então reside nas placas, e a diferença de potencial entre as placas é medida como sendo\(V_0\). Agora, suponha que inserimos um dielétrico que preencha totalmente a lacuna entre as placas. Se monitorarmos a tensão, descobrimos que a leitura do voltímetro caiu para um valor menor\(V\). Escrevemos esse novo valor de tensão como uma fração da tensão original\(V_0\), com um número positivo\(\kappa, \, \kappa > 1\).

    \[V = \frac{1}{\kappa}V_0.\]

    A constante\(\kappa\) nessa equação é chamada de constante dielétrica do material entre as placas e seu valor é característico do material. Uma explicação detalhada de por que o dielétrico reduz a tensão é dada na próxima seção. Diferentes materiais têm diferentes constantes dielétricas (uma tabela de valores para materiais típicos é fornecida na próxima seção). Depois que a bateria é desconectada, não há caminho para que uma carga flua para a bateria a partir das placas do capacitor. Portanto, a inserção do dielétrico não tem efeito sobre a carga na placa, que permanece em um valor de\(Q_0\). Portanto, descobrimos que a capacitância do capacitor com um dielétrico é

    \[C = \frac{Q_0}{V} = \frac{Q_0}{V_0/\kappa} = \kappa \frac{Q_0}{V_0} = \kappa C_0. \label{eq1}\]

    Essa equação nos diz que a capacitância \(C_0\)de um capacitor vazio (vácuo) pode ser aumentada em um fator de \(\kappa\)quando inserimos um material dielétrico para preencher completamente o espaço entre suas placas. Observe que a Equação\ ref {eq1} também pode ser usada para um capacitor vazio por meio da configuração\(\kappa = 1\). Em outras palavras, podemos dizer que a constante dielétrica do vácuo é 1, que é um valor de referência.

    A Figura a mostra um capacitor conectado em série com um interruptor e uma bateria. O interruptor está fechado e há um voltímetro no capacitor, mostrando a leitura V0. As placas do capacitor têm carga +Q0 e —Q0. A Figura b mostra o mesmo circuito, com o interruptor aberto. Isso é rotulado como Etapa 1. O espaço entre as placas do capacitor é cinza, indicando a presença de um dielétrico. Isso é rotulado como Etapa 2. A placa com carga positiva tem sinais negativos no interior, rotulados com —Qi. A placa carregada negativamente tem sinais positivos no interior, rotulados com mais Qi. O voltímetro mostra a leitura V, que é menor que V0.
    Figura\(\PageIndex{1}\): (a) Quando totalmente carregado, um capacitor de vácuo tem tensão\(V_0\) e carga\(Q_0\) (as cargas permanecem nas superfícies internas da placa; o esquema indica o sinal de carga em cada placa). (b) Na etapa 1, a bateria está desconectada. Em seguida, na etapa 2, um dielétrico (que é eletricamente neutro) é inserido no capacitor carregado. Quando a tensão no capacitor agora é medida, verifica-se que o valor da tensão diminuiu para\(V = V_0/\kappa\). O esquema indica o sinal da carga induzida que agora está presente nas superfícies do material dielétrico entre as placas.

    O princípio expresso pela Equação\ ref {eq1} é amplamente utilizado na indústria da construção (Figura\(\PageIndex{2}\)). Placas de metal em um localizador eletrônico de pinos atuam efetivamente como um capacitor. Você coloca um localizador de pinos com o lado plano na parede e o move continuamente na direção horizontal. Quando o localizador se move sobre um pino de madeira, a capacitância de suas placas muda, porque a madeira tem uma constante dielétrica diferente de uma parede de gesso. Essa alteração aciona um sinal em um circuito e, assim, o pino é detectado.

    A Figura a é uma fotografia da mão de uma pessoa segurando um localizador eletrônico contra a parede. A Figura b mostra a seção transversal de uma parede com um pino de madeira atrás dela. O localizador eletrônico de pinos está sendo deslizado pela parede do outro lado. Tem placas de capacitor que tocam a parede.
    Figura\(\PageIndex{2}\): Um localizador eletrônico de pinos é usado para detectar pinos de madeira atrás do drywall.

    A energia elétrica armazenada por um capacitor também é afetada pela presença de um dielétrico. Quando a energia armazenada em um capacitor vazio é\(U_0\), a energia\(U\) armazenada em um capacitor com um dielétrico é menor em um fator de\(\kappa\).

    \[U = \dfrac{1}{2} \dfrac{Q^2}{C} = \dfrac{1}{2} \dfrac{Q_0^2}{\kappa C_0} = \frac{1}{\kappa} U_0. \label{8.12}\]

    Quando uma amostra de material dielétrico é trazida para perto de um capacitor carregado vazio, a amostra reage ao campo elétrico das cargas nas placas do capacitor. Assim como aprendemos em Cargas elétricas e campos sobre eletrostática, haverá cargas induzidas na superfície da amostra; no entanto, elas não são cargas gratuitas como em um condutor, porque um isolador perfeito não tem cargas que se movem livremente. Essas cargas induzidas na superfície dielétrica são de um sinal oposto às cargas livres nas placas do capacitor e, portanto, são atraídas pelas cargas livres nas placas. Consequentemente, o dielétrico é “puxado” para dentro da lacuna, e o trabalho para polarizar o material dielétrico entre as placas é feito às custas da energia elétrica armazenada, que é reduzida, de acordo com a Equação\ ref {8.12}.

    Exemplo\(\PageIndex{1}\): Inserting a Dielectric into an Isolated Capacitor

    Um capacitor vazio de 20,0 pF é carregado até uma diferença de potencial de 40,0 V. A bateria de carregamento é então desconectada e um pedaço de Teflon™ com uma constante dielétrica de 2,1 é inserido para preencher completamente o espaço entre as placas do capacitor (veja a Figura\(\PageIndex{1}\)). Quais são os valores de:

    1. a capacitância,
    2. a carga da placa,
    3. a diferença de potencial entre as placas, e
    4. a energia armazenada no capacitor com e sem dielétrico?

    Estratégia

    Identificamos a capacitância original\(C_0 = 20.0 \, pF\) e a diferença de potencial original\(V_0 = 40.0 \, V\) entre as placas. Combinamos a Equação\ ref {eq1} com outras relações envolvendo capacitância e substituto.

    Solução

    a. A capacitância aumenta para\[C = \kappa C_0 = 2.1(20.0 \, pF) = 42.0 \, pF. \nonumber\]

    b. Sem dielétrico, a carga nas placas é\[Q_0 = C_0V_0 = (20.0 \, pF)(40.0 \, V) = 0.8 \, nC. \nonumber\] Como a bateria é desconectada antes que o dielétrico seja inserido, a carga da placa não é afetada pelo dielétrico e permanece em 0,8 nC.

    c. Com o dielétrico, a diferença de potencial se torna\[V = \frac{1}{\kappa}V_0 = \frac{1}{2.1}40.0 \, V = 19.0 \, V.\nonumber\]

    d. A energia armazenada sem o dielétrico é\[U_0 = \frac{1}{2}C_0V_0^2 = \frac{1}{2}(20.0 \, pF)(40.0 \, V)^2 = 16.0 \, nJ. \nonumber\] Com o dielétrico inserido, usamos a Equação\ ref {8.12} para descobrir que a energia armazenada diminui para\[U = \frac{1}{\kappa}U_0 = \frac{1}{2.1} 16.0 \, nJ = 7.6 \, nJ. \nonumber\]

    Significância

    Observe que o efeito de um dielétrico na capacitância de um capacitor é um aumento drástico de sua capacitância. Esse efeito é muito mais profundo do que uma mera mudança na geometria de um capacitor.

    Exercício\(\PageIndex{1}\)

    Quando um dielétrico é inserido em um capacitor isolado e carregado, a energia armazenada diminui para 33% de seu valor original.

    1. O que é a constante dielétrica?
    2. Como a capacitância muda?
    Resposta

    a. 3,0; b.\(C = 3.0 \, C_0\)