7.6: Superfícies e condutores equipotenciais

Objetivos de

Ao final desta seção, você poderá:

• Defina superfícies equipotenciais e linhas equipotenciais
• Explicar a relação entre linhas equipotenciais e linhas de campo elétrico
• Mapeie linhas equipotenciais para cargas de um ou dois pontos
• Descreva o potencial de um condutor
• Compare e contraste linhas equipotenciais e linhas de elevação em mapas topográficos

Podemos representar potenciais elétricos (voltagens) de forma pictórica, assim como desenhamos imagens para ilustrar campos elétricos. Isso não é surpreendente, já que os dois conceitos estão relacionados. Considere a Figura \(\PageIndex{1}\), que mostra uma carga pontual positiva isolada e suas linhas de campo elétrico, que irradiam de uma carga positiva e terminam com cargas negativas. Usamos setas azuis para representar a magnitude e a direção do campo elétrico e usamos linhas verdes para representar lugares onde o potencial elétrico é constante. Eles são chamados de superfície equipotencial s em três dimensões, ou linha equipotencial s em duas dimensões. O termo equipotencial também é usado como substantivo, referindo-se a uma linha ou superfície equipotencial. O potencial para uma carga pontual é o mesmo em qualquer lugar em uma esfera imaginária de raio r ao redor da carga. Isso é verdade porque o potencial de uma carga pontual é dado por\(V = kq/r\) e, portanto, tem o mesmo valor em qualquer ponto que esteja a uma determinada distância r da carga. Uma esfera equipotencial é um círculo na visão bidimensional da Figura\(\PageIndex{1}\). Como as linhas do campo elétrico apontam radialmente para longe da carga, elas são perpendiculares às linhas equipotenciais.

Figura\(\PageIndex{1}\): Uma carga pontual isolada Q com suas linhas de campo elétrico em azul e linhas equipotenciais em verde. O potencial é o mesmo ao longo de cada linha equipotencial, o que significa que nenhum trabalho é necessário para mover uma carga em qualquer lugar ao longo de uma dessas linhas. É necessário trabalhar para mover uma carga de uma linha equipotencial para outra. As linhas equipotenciais são perpendiculares às linhas do campo elétrico em todos os casos. Para uma versão tridimensional, explore o primeiro link de mídia.

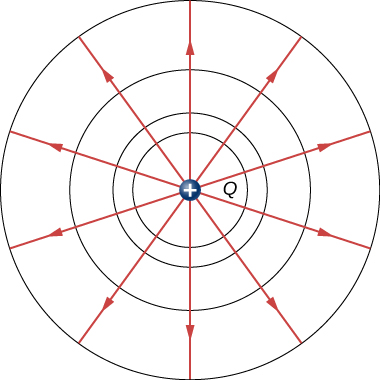
É importante observar que as linhas equipotenciais são sempre perpendiculares às linhas do campo elétrico. Nenhum trabalho é necessário para mover uma carga ao longo de um equipotencial, uma vez que\(\Delta V = 0\). Assim, o trabalho é

\[W = - \Delta U = - q\Delta V = 0.\]

O trabalho é zero se a direção da força for perpendicular ao deslocamento. A força está na mesma direção que\(E\), então o movimento ao longo de um equipotencial deve ser perpendicular\(E\) a. Mais precisamente, o trabalho está relacionado ao campo elétrico por

\ [\ begin {align} W &=\ vec {F}\ cdot\ vec {d}\ label {eq5} \\ [4pt] &= q\ vec {E}\ cdot\ vec {d}\ nonumber\\ [4pt] &= QEd \,\ cos\,\ theta\ nonumber\\ [4pt] &= 0. \ nonumber\ end {align} \ nonumber\]

Observe isso na Equação\ ref {eq5}\(E\) e\(F\) simbolize as magnitudes do campo elétrico e da força, respectivamente. \(q\)Nem\(E\) é zero e também não\(d\) é zero. Então\ (\ cos\, \ theta\) deve ser 0, o que significa que\(\theta\) deve ser\(90^o\). Em outras palavras, o movimento ao longo de um equipotencial é perpendicular a E.

Uma das regras para campos elétricos e condutores estáticos é que o campo elétrico deve ser perpendicular à superfície de qualquer condutor. Isso implica que um condutor é uma superfície equipotencial em situações estáticas. Não pode haver diferença de tensão na superfície de um condutor, ou as cargas fluirão. Um dos usos desse fato é que um condutor pode ser fixado no que consideramos zero volts conectando-o à terra com um bom condutor - um processo chamado aterramento. O aterramento pode ser uma ferramenta de segurança útil. Por exemplo, aterrar a caixa metálica de um aparelho elétrico garante que ela esteja a zero volts em relação à Terra.

Figura\(\PageIndex{2}\): As linhas do campo elétrico e as linhas equipotenciais para duas cargas iguais, mas opostas. As linhas equipotenciais podem ser desenhadas tornando-as perpendiculares às linhas do campo elétrico, se forem conhecidas. Observe que o potencial é maior (mais positivo) próximo à carga positiva e menor (mais negativo) perto da carga negativa. Para uma versão tridimensional, explore o primeiro link de mídia.

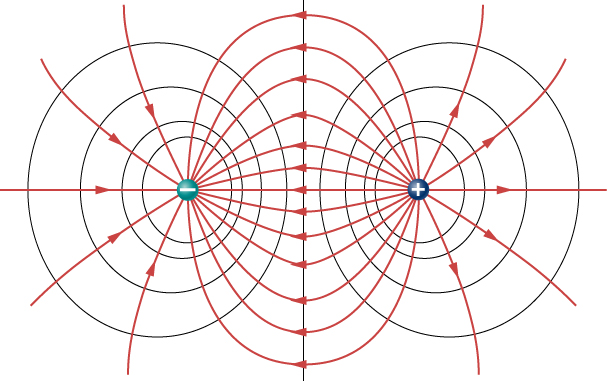
Como um condutor é equipotencial, ele pode substituir qualquer superfície equipotencial. Por exemplo, na Figura\(\PageIndex{2}\), um condutor esférico carregado pode substituir a carga pontual, e o campo elétrico e as superfícies potenciais externas a ele permanecerão inalterados, confirmando a alegação de que uma distribuição esférica de carga é equivalente a uma carga pontual em seu centro.

A figura\(\PageIndex{2}\) mostra o campo elétrico e as linhas equipotenciais para duas cargas iguais e opostas. Dadas as linhas do campo elétrico, as linhas equipotenciais podem ser desenhadas simplesmente tornando-as perpendiculares às linhas do campo elétrico. Por outro lado, dadas as linhas equipotenciais, como na Figura \(\PageIndex{2a}\), as linhas do campo elétrico podem ser desenhadas tornando-as perpendiculares aos equipotenciais, como na Figura \(\PageIndex{2b}\).

Figura\(\PageIndex{3}\): (a) Essas linhas equipotenciais podem ser medidas com um voltímetro em um experimento de laboratório. (b) As linhas de campo elétrico correspondentes são encontradas desenhando-as perpendicularmente aos equipotenciais. Observe que esses campos são consistentes com duas cargas negativas iguais. Para uma versão tridimensional, jogue com o primeiro link de mídia.

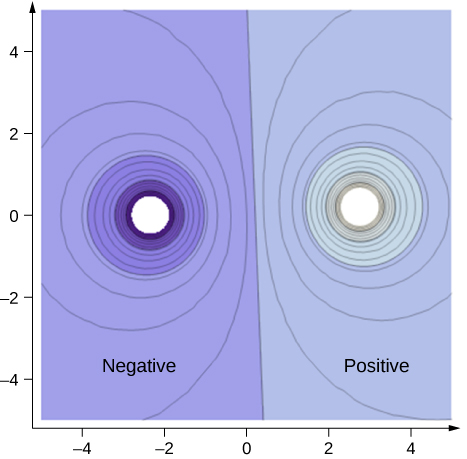
Para melhorar sua intuição, mostramos uma variante tridimensional do potencial em um sistema com duas cargas opostas. A figura \(\PageIndex{4}\) mostra um mapa tridimensional do potencial elétrico, onde as linhas no mapa são para superfícies equipotenciais. A colina está com carga positiva e a calha está com carga negativa. O potencial está zero longe das cobranças. Observe que o corte em um potencial específico implica que as cargas estão em esferas condutoras com um raio finito.

Figura \(\PageIndex{4}\): Mapa do potencial elétrico de duas cargas opostas de igual magnitude em esferas condutoras. O potencial é negativo perto da carga negativa e positivo perto da carga positiva. Esta imagem dinâmica é alimentada pelo CalcPlot3d e pode ser visualizada\ (\ PageIndex {4}\) Mapa de potencial elétrico II” mt-page-link-identifier="91122f512ec949b78025ae238d164cf2" href=” /learning_objects/visualizations_and_simulations/calcplot3d_interactive_figFísicas/Físicas_Figuras/Figura_7.5.4_Electric_Potencial_ Map_II"> aqui.

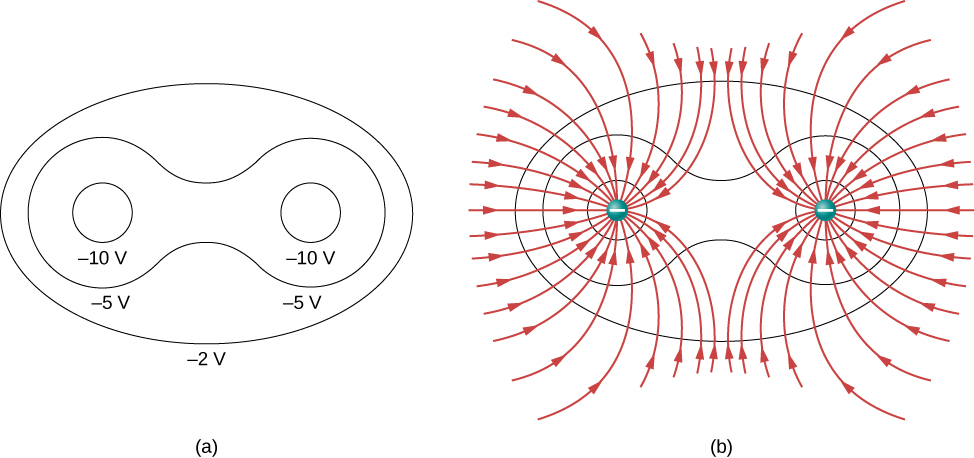
Um mapa bidimensional do plano da seção transversal que contém as duas cargas é mostrado na Figura\(\PageIndex{5}\). A linha que está equidistante das duas cargas opostas corresponde ao potencial zero, pois nos pontos da linha, o potencial positivo da carga positiva cancela o potencial negativo da carga negativa. As linhas equipotenciais no plano da seção transversal são ciclos fechados, que não são necessariamente círculos, pois em cada ponto, o potencial líquido é a soma dos potenciais de cada carga.

Figura\(\PageIndex{5}\): Uma seção transversal do mapa de potencial elétrico de duas cargas opostas de igual magnitude. O potencial é negativo perto da carga negativa e positivo perto da carga positiva.

Nota

Veja esta simulação para observar e modificar as superfícies equipotenciais e os campos elétricos para muitas configurações de carga padrão. Há muito para explorar.

Um dos casos mais importantes é o das conhecidas placas condutoras paralelas mostradas na Figura\(\PageIndex{6}\). Entre as placas, os equipotenciais são uniformemente espaçados e paralelos. O mesmo campo poderia ser mantido colocando placas condutoras nas linhas equipotenciais nos potenciais mostrados.

Figura\(\PageIndex{6}\): O campo elétrico e as linhas equipotenciais entre duas placas de metal. Observe que o campo elétrico é perpendicular aos equipotenciais e, portanto, normal às placas em sua superfície, bem como no centro da região entre elas.

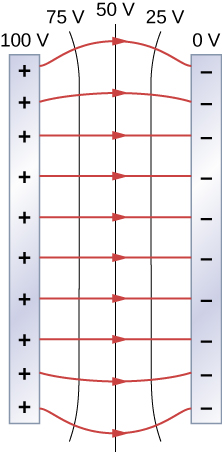
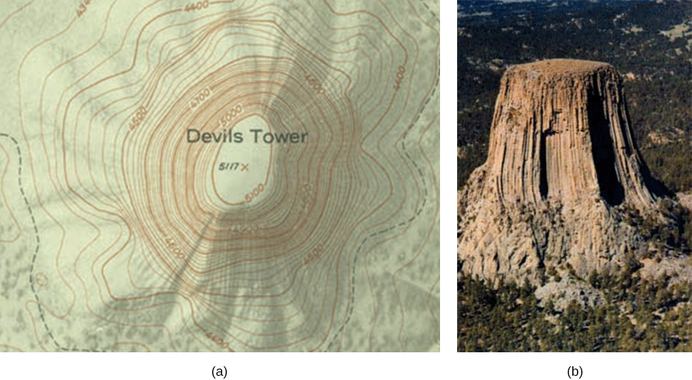
Considere as placas paralelas Figura\(\PageIndex{6}\). Eles têm linhas equipotenciais que são paralelas às placas no espaço entre elas e espaçadas uniformemente. Um exemplo disso (com valores de amostra) é dado na Figura\(\PageIndex{6}\). Poderíamos desenhar um conjunto similar de isolinhas equipotenciais para a gravidade em colinas. Se a colina tiver alguma extensão na mesma inclinação, as linhas isométricas ao longo dessa extensão seriam paralelas umas às outras. Além disso, em regiões de inclinação constante, as isolinhas seriam espaçadas uniformemente. Um exemplo de linhas topográficas reais é mostrado na Figura\(\PageIndex{7}\).

Figura\(\PageIndex{6}\). (a) Um mapa topográfico da Devil's Tower, Wyoming. Linhas próximas indicam terrenos muito íngremes. (b) Uma foto em perspectiva da Devil's Tower mostra o quão íngremes são suas laterais. Observe que o topo da torre tem a mesma forma do centro do mapa topográfico.

Exemplo\(\PageIndex{1}\): Calculando linhas equipotenciais

Você viu as linhas equipotenciais de uma carga pontual na Figura\(\PageIndex{1}\). Como os calculamos? Por exemplo, se tivermos uma\(+10-nC\) carga na origem, quais são as superfícies equipotenciais nas quais o potencial é (a) 100 V, (b) 50 V, (c) 20 V e (d) 10 V?

Estratégia

Defina a equação para o potencial de uma carga pontual igual a uma constante e resolva a (s) variável (s) restante (s). Em seguida, calcule os valores conforme necessário.

Solução

No\(V = k\dfrac{q}{r}\), deixe V ser uma constante. A única variável restante é r; portanto,\ (r = k\ dfrac {q} {V} = constante\). Assim, as superfícies equipotenciais são esferas sobre a origem. Suas localizações são:

1. \ (r = k\ dfrac {q} {V} =\ left (8,99\ times 10^9\, Nm^2/C^2\ direita) \ dfrac {(10\ times 10^ {-9} C)} {100\, V} = 0,90\, m\);
2. \ (r = k\ dfrac {q} {V} =\ left (8,99\ times 10^9\, Nm^2/C^2\ direita) \ dfrac {(10\ times 10^ {-9} C)} {50\, V} = 1,8\, m\);
3. \ (r = k\ dfrac {q} {V} =\ left (8,99\ times 10^9\, Nm^2/C^2\ direita) \ dfrac {(10\ times 10^ {-9} C)} {20\, V} = 4,5\, m\);
4. \ (r = k\ dfrac {q} {V} =\ left (8,99\ times 10^9\, Nm^2/C^2\ right) \ dfrac {(10\ times 10^ {-9} C)} {10\, V} = 9,0\, m\).

Significância

Isso significa que superfícies equipotenciais em torno de uma carga pontual são esferas de raio constante, como mostrado anteriormente, com localizações bem definidas.

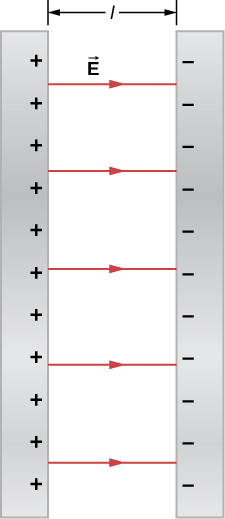
Exemplo\(\PageIndex{2}\): diferença de potencial entre placas paralelas de carga oposta

Duas grandes placas condutoras carregam cargas iguais e opostas, com uma densidade\(\sigma\) de carga superficial de magnitude\ (6,81\ times 10^ {-7} C/m\), conforme mostrado na Figura\(\PageIndex{8}\). A separação entre as placas é\(l = 6.50 \, mm\).

1. Qual é o campo elétrico entre as placas?
2. Qual é a diferença de potencial entre as placas?
3. Qual é a distância entre planos equipotenciais que diferem em 100 V?

Figura\(\PageIndex{8}\): O campo elétrico entre placas paralelas de carga oposta. Uma porção é liberada na placa positiva.

Estratégia

1. Como as placas são descritas como “grandes” e a distância entre elas não é, vamos aproximar cada uma delas como um plano infinito e aplicar o resultado da lei de Gauss no capítulo anterior.
2. Use\(\Delta V_{AB} = - \int_A^B \vec{E} \cdot d\vec{l}\).
3. Como o campo elétrico é constante, encontre a razão de 100 V com a diferença de potencial total; em seguida, calcule essa fração da distância.

Solução

a. O campo elétrico é direcionado da placa positiva para a negativa, conforme mostrado na figura, e sua magnitude é dada por

\ [\ begin {align*} E &=\ dfrac {\ sigma} {\ epsilon_0}\\ [4pt] &=\ dfrac {6,81\ times 10^ {-7} C/m^2} {8,85\ vezes 10^ {-12} C^2/N \ cdot m^2}\\ [4pt] &= 7,69\ times 10^4\, V/m.\ end {align*} \]

b. Para encontrar a diferença de potencial\(\Delta V\) entre as placas, usamos um caminho da placa negativa para a positiva que é direcionado contra o campo. O vetor de deslocamento\(d\vec{l}\) e o campo elétrico\(\vec{E}\) são antiparalelos, então\ (\ vec {E} \ cdot d\ vec {l} = - E\, dl\). A diferença de potencial entre a placa positiva e a placa negativa é então

\ [\ begin {align*}\ Delta V &= -\ int E\ cdot dl\\ [4pt] &= E\ int dl\\ [4pt] &= El\\ [4pt] &= (7,69\ times 10^4 V/m) (6,50\ times 10^ {-3} m)\\ [4pt] &= 500\, V\ end {align*} \]

c. A diferença de potencial total é de 500 V, então 1/5 da distância entre as placas será a distância entre as diferenças de potencial de 100 V. A distância entre as placas é de 6,5 mm, portanto, haverá 1,3 mm entre as diferenças de potencial de 100 V.

Significância

Agora você viu um cálculo numérico das localizações dos equipotenciais entre duas placas paralelas carregadas.

Exercício\(\PageIndex{1}\)

Quais são as superfícies equipotenciais para uma carga de linha infinita?

Responda

cilindros infinitos de raio constante, com a carga de linha como eixo

Distribuição de cargas em condutores

Em Exemplo\(\PageIndex{1}\) com uma carga pontual, descobrimos que as superfícies equipotenciais estavam na forma de esferas, com a carga pontual no centro. Dado que uma esfera condutora em equilíbrio eletrostático é uma superfície esférica equipotencial, devemos esperar que possamos substituir uma das superfícies em \(\PageIndex{2}\) Exemplo por uma esfera condutora e ter uma solução idêntica fora da esfera. No entanto, o interior será bem diferente.

Figura\(\PageIndex{9}\): Uma esfera condutora isolada.

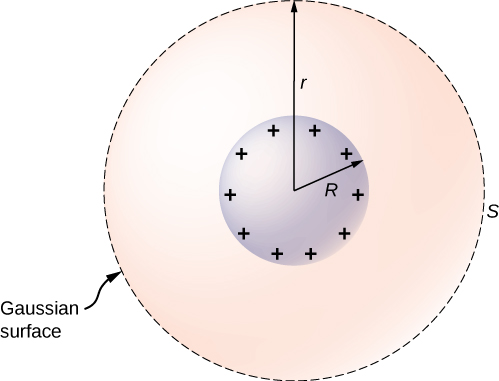
Para investigar isso, considere a esfera condutora isolada da Figura\(\PageIndex{9}\) que tem um raio R e uma carga excessiva q. Para encontrar o campo elétrico dentro e fora da esfera, observe que a esfera está isolada, então sua distribuição de mudança de superfície e o campo elétrico dessa distribuição são esfericamente simétricos. Portanto, podemos representar o campo como\(\vec{E} = E(r)\hat{r}\). Para calcular\(E(r)\), aplicamos a lei de Gauss sobre uma superfície esférica fechada S de raio r que é concêntrica com a esfera condutora. Como\(r\) é constante e está\(\hat{n} = \hat{r}\) na esfera,

\ [\ begin {align}\ oint\ vec {E}\ cdot\ hat {n}\, da &= E (r) \ oint da\\[4pt] &=E(r) 4\pi r^2. \end{align}\]

\(S\)Pois\(r < R\), está dentro do condutor, então lembre-se de nosso estudo anterior da lei de Gauss que\(q_{enc} = 0\) e a lei de Gauss fornecem\(E(r) = 0\), como esperado, dentro de um condutor em equilíbrio. Se\(r > R\), S encerra o condutor assim \(q_{enc} = q\). Da lei de Gauss,

\[E(r) 4\pi r^2 = \dfrac{q}{\epsilon_0}.\]

O campo elétrico da esfera pode, portanto, ser escrito como

\[E = 0 \, (r < R),\]

e

\ [E =\ dfrac {1} {4\ pi\ epsilon_0}\ dfrac {q} {r^2}\ hat {r}\, (r \ geq R).\]

Como esperado, na região\(r \geq R\), o campo elétrico devido a uma carga q colocada em uma esfera condutora isolada de raio R é idêntico ao campo elétrico de uma carga pontual q localizada no centro da esfera.

Para encontrar o potencial elétrico dentro e fora da esfera, observe que\(r \geq R\), para, o potencial deve ser o mesmo de uma carga pontual isolada q localizada em\(r = 0\),

\ [V (r) =\ dfrac {1} {4\ pi\ epsilon_0}\ dfrac {q} {r} (r\ geq R)\]

simplesmente devido à semelhança do campo elétrico.

Pois\(r < R, \, E = 0\), então V (r) é constante nessa região. Uma vez que\(V(R) = q/4\pi \epsilon_0 R\),

\ [V (r) =\ dfrac {1} {4\ pi\ epsilon_0}\ dfrac {q} {R} (r < R).\]

Usaremos esse resultado para mostrar que

\[\sigma_1 R_1 = \sigma_2 R_2,\]

para duas esferas condutoras de raios\(R_1\) e\(R_2\), com densidades de carga superficial\(\sigma_1\) e\(\sigma_2\) respectivamente, conectadas por um fio fino, conforme mostrado na Figura \(\PageIndex{10}\). As esferas estão suficientemente separadas para que cada uma possa ser tratada como se estivesse isolada (além do fio). Observe que a conexão pelo fio significa que todo esse sistema deve ser equipotencial.

Figura\(\PageIndex{10}\): Duas esferas condutoras são conectadas por um fio condutor fino.

Acabamos de ver que o potencial elétrico na superfície de uma esfera condutora isolada e carregada de raio R é

\[V = \dfrac{1}{4\pi \epsilon_0} \dfrac{q}{R}.\]

Agora, as esferas são conectadas por um condutor e, portanto, têm o mesmo potencial; portanto

\ [\ dfrac {1} {4\ pi\ epsilon_0}\ dfrac {q_1} {R_1} =\ dfrac {1} {4\ pi r\ epsilon_0}\ dfrac {q_2} {R_2},\] e

\[\dfrac{q_1}{R_1} = \dfrac{q_2}{R_2}.\]

A carga líquida em uma esfera condutora e sua densidade de carga superficial estão relacionadas por\(q = \sigma (4\pi R^2)\). Substituindo essa equação pela anterior, encontramos

\[\sigma_1 R_1 = \sigma_2 R_2.\]

Obviamente, duas esferas conectadas por um fio fino não constituem um condutor típico com um raio de curvatura variável. No entanto, esse resultado fornece pelo menos uma ideia qualitativa de como a densidade de carga varia na superfície de um condutor. A equação indica que onde o raio de curvatura é grande (pontos B e D em\(\PageIndex{11}\)) \(\sigma\) e E são pequenos.

Da mesma forma, as cargas tendem a ser mais densas onde a curvatura da superfície é maior, conforme demonstrado pela distribuição de carga em metal de formato estranho (Figura\(\PageIndex{11}\)). A densidade de carga superficial é maior em locais com um pequeno raio de curvatura do que em locais com um grande raio de curvatura.

Figura\(\PageIndex{11}\): A densidade de carga superficial e o campo elétrico de um condutor são maiores em regiões com raios de curvatura menores.

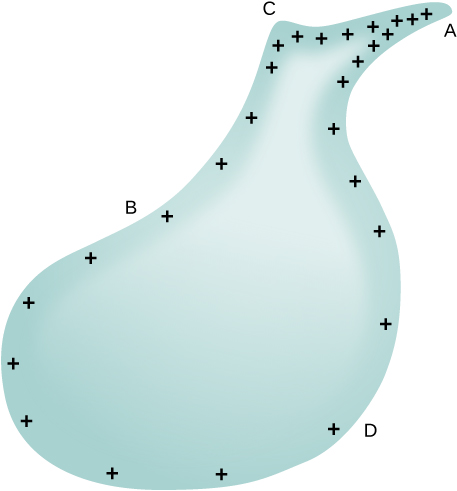
Uma aplicação prática desse fenômeno é o pára-raios, que é simplesmente uma haste de metal aterrada com uma extremidade afiada apontando para cima. À medida que a carga positiva se acumula no solo devido a uma nuvem carregada negativamente no alto, o campo elétrico ao redor da ponta afiada fica muito grande. Quando o campo atinge um valor de aproximadamente\(3.0 \times 10^6 N/C\) (a força dielétrica do ar), os íons livres no ar são acelerados para energias tão altas que suas colisões com moléculas de ar realmente ionizam as moléculas. Os elétrons livres resultantes no ar então fluem através da haste para a Terra, neutralizando assim parte da carga positiva. Isso evita que o campo elétrico entre a nuvem e o solo fique grande o suficiente para produzir um raio na região ao redor da haste.

Uma aplicação importante de campos elétricos e linhas equipotenciais envolve o coração. O coração depende de sinais elétricos para manter seu ritmo. O movimento dos sinais elétricos faz com que as câmaras do coração se contraiam e relaxem. Quando uma pessoa tem um ataque cardíaco, o movimento desses sinais elétricos pode ser perturbado. Um marcapasso artificial e um desfibrilador podem ser usados para iniciar o ritmo dos sinais elétricos. As linhas equipotenciais ao redor do coração, da região torácica e do eixo do coração são formas úteis de monitorar a estrutura e as funções do coração. Um eletrocardiograma (ECG) mede os pequenos sinais elétricos gerados durante a atividade do coração.

PhET

Brinque com esta simulação para mover cargas pontuais no campo de jogo e depois ver o campo elétrico, as tensões, as linhas equipotenciais e muito mais.