Skip to main content
Global

7.5: Determinando campo a partir do potencial

  1. Last updated
  2. Save as PDF
  • Page ID
    184841

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Explicar como calcular o campo elétrico em um sistema a partir do potencial dado
    • Calcule o campo elétrico em uma determinada direção a partir de um determinado potencial
    • Calcule o campo elétrico em todo o espaço a partir de um determinado potencial

    Lembre-se de que conseguimos, em certos sistemas, calcular o potencial integrando o campo elétrico. Como você já deve suspeitar, isso significa que podemos calcular o campo elétrico tomando derivadas do potencial, embora passar de uma grandeza escalar para uma vetorial introduza algumas rugas interessantes. Freqüentemente, precisamos calcular\(\vec{E}\) a força em um sistema; como geralmente é mais simples calcular o potencial diretamente, existem sistemas nos quais é útil calcular V e depois derivar\(\vec{E}\) dele.

    Em geral, independentemente de o campo elétrico ser uniforme, ele aponta na direção do potencial decrescente, porque a força em uma carga positiva está na direção de\(\vec{E}\) e também na direção do menor potencial V. Além disso, a magnitude de\(\vec{E}\) é igual à taxa de diminuição de V com a distância. Quanto mais rápido o V diminui com a distância, maior o campo elétrico. Isso nos dá o seguinte resultado.

    Relação entre tensão e campo elétrico uniforme

    Em forma de equação, a relação entre tensão e campo elétrico uniforme é

    \[E = - \dfrac{\Delta V}{\Delta s}\]

    onde\(\Delta s\) está a distância na qual a mudança de potencial\(\Delta V\) ocorre. O sinal de menos nos diz que\(E\) aponta na direção da diminuição do potencial. Diz-se que o campo elétrico é o gradiente (como em grau ou inclinação) do potencial elétrico.

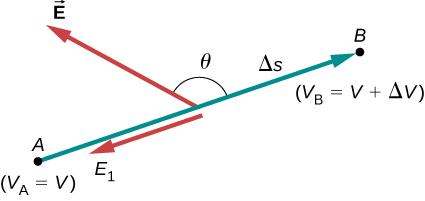
    A figura mostra o componente do campo elétrico de dois pontos A e B separados pela distância delta s e com uma diferença de potencial de delta V.
    Figura\(\PageIndex{1}\): The electric field component along the displacement \(\Delta s\) is given by \(E = - \dfrac{\Delta V}{\Delta s}\). Note that A and B are assumed to be so close together that the field is constant along \(\Delta s\).

    For continually changing potentials, \(\Delta V\) and \(\Delta s\) become infinitesimals, and we need differential calculus to determine the electric field. As shown in Figure \(\PageIndex{1}\), if we treat the distance \(\Delta s\) as very small so that the electric field is essentially constant over it, we find that

    \[E_s = - \dfrac{dV}{ds}.\]

    Therefore, the electric field components in the Cartesian directions are given by

    \[E_x = - \dfrac{\partial V}{\partial x}, \, E_y = - \dfrac{\partial V}{\partial y}, \, E_z = - \dfrac{\partial V}{\partial z}.\]

    This allows us to define the “grad” or “del” vector operator, which allows us to compute the gradient in one step. In Cartesian coordinates, it takes the form

    \[\vec{\nabla} = \hat{i} \dfrac{\partial}{\partial x} + \hat{j} \dfrac{\partial}{\partial y} + \hat{k} \dfrac{\partial}{\partial z}.\]

    With this notation, we can calculate the electric field from the potential with

    \[\vec{E} = - \vec{\nabla}V, \label{eq20}\]

    a process we call calculating the gradient of the potential.

    If we have a system with either cylindrical or spherical symmetry, we only need to use the del operator in the appropriate coordinates:

    \[\begin{align} \vec{\nabla}_{cyl} &= \underbrace{\hat{r} \dfrac{\partial}{\partial r} + \hat{\varphi}\dfrac{1}{r} \dfrac{\partial}{\partial \varphi} + \hat{z} \dfrac{\partial}{\partial z}}_{\text{Cylindrical}} \label{cylindricalnabla} \\[4pt] \vec{\nabla}_{sph} &= \underbrace{ \hat{r} \dfrac{\partial}{\partial r} + \hat{\theta}\dfrac{1}{r} \dfrac{\partial}{\partial \theta} + \hat{\varphi} \dfrac{1}{r \, sin \, \theta}\dfrac{\partial}{\partial \varphi}}_{\text{Spherical}} \label{spherenabla} \end{align}\]

    Example \(\PageIndex{1}\): Electric Field of a Point Charge

    Calculate the electric field of a point charge from the potential.

    Strategy

    The potential is known to be \(V = k\dfrac{q}{r}\), which has a spherical symmetry. Therefore, we use the spherical del operator (Equation \ref{spherenabla}) into Equation \ref{eq20}:

    \[\vec{E} = - \vec{\nabla}_{sph} V \nonumber.\]

    Solution

    Performing this calculation gives us

    \[\begin{align*} \vec{E} &= - \left( \hat{r}\dfrac{\partial}{\partial r} + \hat{\theta}\dfrac{1}{r} \dfrac{\partial}{\partial \theta} + \hat{\varphi}\dfrac{1}{1 \, \sin \, \theta} \dfrac{\partial}{\partial \varphi}\right) k\dfrac{q}{r} \\[4pt] &= - k\left( \hat{r}\dfrac{\partial}{\partial r}\dfrac{1}{r} + \hat{\theta}\dfrac{1}{r} \dfrac{\partial}{\partial \theta}\dfrac{1}{r} + \hat{\varphi}\dfrac{1}{1 \, \sin \, \theta} \dfrac{\partial}{\partial \varphi}\dfrac{1}{r}\right).\end{align*}\]

    This equation simplifies to

    \[\vec{E} = - kq\left(\hat{r}\dfrac{-1}{r^2} + \hat{\theta}0 + \hat{\varphi}0 \right) = k\dfrac{q}{r^2}\hat{r} \nonumber\]

    as expected.

    Significance

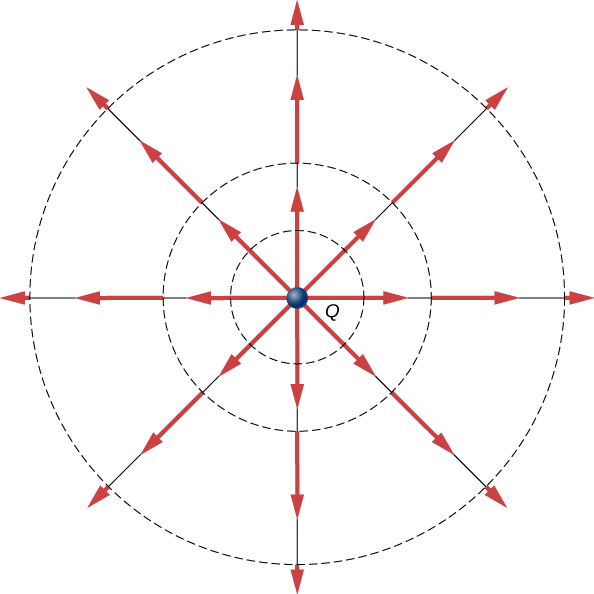
    We not only obtained the equation for the electric field of a point particle that we’ve seen before, we also have a demonstration that \(\vec{E}\) points in the direction of decreasing potential, as shown in Figure \(\PageIndex{2}\).

    The figure shows a charge Q and radially outward electric field vectors from Q.
    Figure \(\PageIndex{2}\): Electric field vectors inside and outside a uniformly charged sphere.
    Example \(\PageIndex{2}\): Electric Field of a Ring of Charge

    Use the potential found previously to calculate the electric field along the axis of a ring of charge (Figure \(\PageIndex{3}\)).

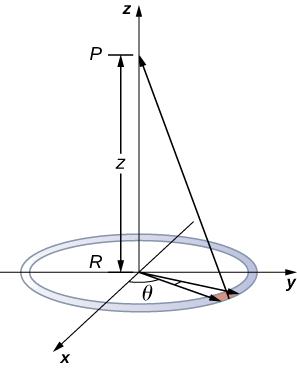
    The figure shows a ring of charge located on the xy-plane with its center at the origin. Point P is located on the z-axis at distance z away from the origin.
    Figure \(\PageIndex{3}\): We want to calculate the electric field from the electric potential due to a ring charge.

    Strategy

    In this case, we are only interested in one dimension, the z-axis. Therefore, we use

    \[E_z = - \dfrac{\partial V}{\partial z} \nonumber\]

    with the potential

    \[V = k \dfrac{q_{tot}}{\sqrt{z^2 + R^2}} \nonumber\]

    found previously.

    Solution

    Taking the derivative of the potential yields

    \[ \begin{align*} E_z &= - \dfrac{\partial}{\partial z} \dfrac{kq_{tot}}{\sqrt{z^2 + R^2}} \\[4pt] &= k \dfrac{q_{tot}z}{(z^2 + R^2)^{3/2}}. \end{align*}\]

    Significance

    Again, this matches the equation for the electric field found previously. It also demonstrates a system in which using the full del operator is not necessary.

    Exercise \(\PageIndex{1}\)

    Which coordinate system would you use to calculate the electric field of a dipole?

    Answer

    Any, but cylindrical is closest to the symmetry of a dipole.