7.4: Cálculos do potencial elétrico
- Page ID
- 184791
Ao final desta seção, você poderá:
- Calcule o potencial devido a uma cobrança de pontos
- Calcule o potencial de um sistema de cobranças de vários pontos
- Descreva um dipolo elétrico
- Defina o momento de dipolo
- Calcule o potencial de uma distribuição contínua de carga
Cargas pontuais, como elétrons, estão entre os elementos fundamentais da matéria. Além disso, distribuições esféricas de carga (como carga em uma esfera de metal) criam campos elétricos externos exatamente como uma carga pontual. O potencial elétrico devido a uma carga pontual é, portanto, um caso que precisamos considerar.
Podemos usar o cálculo para encontrar o trabalho necessário para mover uma carga de teste q de uma grande distância para uma distância de r de uma carga pontual q. Observando a conexão entre trabalho e potencial\(W = -q\Delta V\), como na última seção, podemos obter o seguinte resultado.
O potencial elétrico\(V\) de uma carga pontual é dado por
\[\underbrace{V = \dfrac{kq}{r}}_{\text{point charge}} \label{PointCharge}\]
onde\(k\) é uma constante igual\(9.0 \times 10^9 \, N \cdot m^2/C^2\) a.
O potencial na Equação\ ref {PointCharge} no infinito é escolhido como zero. Assim,\(V\) para um ponto, a carga diminui com a distância, enquanto que\(\vec{E}\) para um ponto, a carga diminui com a distância ao quadrado:
\[E = \dfrac{F}{q_t} = \dfrac{kq}{r^2}\]
Lembre-se de que o potencial elétrico V é escalar e não tem direção, enquanto o campo elétrico\(\vec{E}\) é um vetor. Para encontrar a voltagem devido a uma combinação de cargas pontuais, você adiciona as voltagens individuais como números. Para encontrar o campo elétrico total, você deve adicionar os campos individuais como vetores, levando em consideração a magnitude e a direção. Isso é consistente com o fato de que V está intimamente associado à energia, um escalar, enquanto\(\vec{E}\) está intimamente associado à força, um vetor.
As cargas na eletricidade estática estão normalmente na\((\mu C)\) faixa de nanocoulomb (nC) a microcoulomb. Qual é a voltagem a 5,00 cm do centro de uma esfera de metal sólido de 1 cm de diâmetro que tem uma carga estática de —3,00 nC?
Estratégia
Conforme discutimos em Cargas e Campos Elétricos, a carga em uma esfera de metal se espalha uniformemente e produz um campo como o de uma carga pontual localizada em seu centro. Assim, podemos encontrar a voltagem usando a equação\(V = \dfrac{kq}{r}\).
Solução
Inserindo valores conhecidos na expressão para o potencial de uma carga pontual (Equation\ ref {pointCharge}), obtemos
\[\begin{align} V &= k\dfrac{q}{r} \nonumber \\[4pt] &= (9.00 \times 10^9 \, N \cdot m^2/C^2)\left(\dfrac{-3.00 \times 10^{-9}C}{5.00 \times 10^{-2}m}\right) \nonumber \\[4pt] &= - 539 \, V. \nonumber \end{align} \nonumber \]
Significância
O valor negativo da tensão significa que uma carga positiva seria atraída de uma distância maior, já que o potencial é menor (mais negativo) do que em distâncias maiores. Por outro lado, uma carga negativa seria repelida, conforme esperado.
Uma demonstração do gerador Van de Graaff tem uma esfera metálica de 25,0 cm de diâmetro que produz uma tensão de 100 kV perto de sua superfície (Figura). Qual excesso de carga reside na esfera? (Suponha que cada valor numérico aqui seja mostrado com três números significativos.)
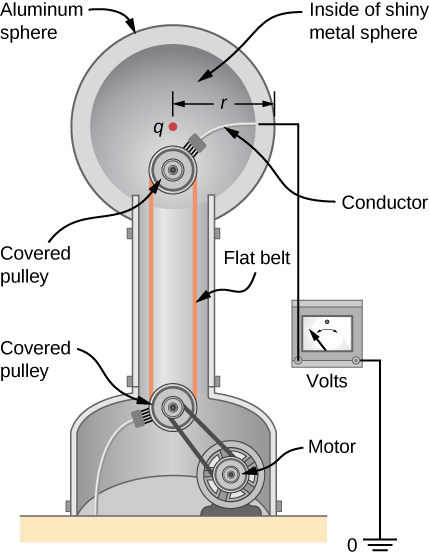
Estratégia
O potencial na superfície é o mesmo de uma carga pontual no centro da esfera, a 12,5 cm de distância. (O raio da esfera é 12,5 cm.) Assim, podemos determinar o excesso de carga usando a Equação\ ref {pointCharge}
\[V = \dfrac{kq}{r}.\]
Solução
Resolver\(q\) e inserir valores conhecidos fornece
\[\begin{align} q &= \dfrac{rV}{k} \nonumber \\[4pt] &= \dfrac{(0.125 \, m)(100 \times 10^3 \, V)}{8.99 \times 10^9 N \cdot m^2/C^2} \nonumber \\[4pt] &= 1.39 \times 10^{-6} C \nonumber \\[4pt] &= 1.39 \, \mu C. \nonumber \end{align} \nonumber \]
Significância
Essa é uma carga relativamente pequena, mas produz uma voltagem bastante grande. Temos outra indicação aqui de que é difícil armazenar cobranças isoladas.
Qual é o potencial dentro da esfera metálica em Example\(\PageIndex{1}\)?
Solução
\[\begin{align} V &= k\dfrac{q}{r} \nonumber \\[4pt] &= (8.99 \times 10^9 N \cdot m^2/C^2) \left(\dfrac{-3.00 \times 10^{-9} C}{5.00 \times 10^{-3} m}\right) \nonumber \\[4pt] &= - 5390 \, V\nonumber \end{align} \nonumber \]
Lembre-se de que o campo elétrico dentro de um condutor é zero. Portanto, qualquer caminho de um ponto na superfície até qualquer ponto no interior terá um integrando de zero ao calcular a mudança no potencial e, portanto, o potencial no interior da esfera é idêntico ao da superfície.
As tensões em ambos os exemplos podem ser medidas com um medidor que compara o potencial medido com o potencial do solo. O potencial do solo geralmente é considerado zero (em vez de considerar o potencial no infinito como zero). É a diferença de potencial entre dois pontos que é importante, e muitas vezes há uma suposição tácita de que algum ponto de referência, como a Terra ou um ponto muito distante, tem potencial zero. Conforme observado anteriormente, isso é análogo à medição do nível do mar, como\(h = 0\) quando se considera a energia potencial gravitacional\(U_g = mgh\).
Sistemas de cobranças de vários pontos
Assim como o campo elétrico obedece a um princípio de superposição, o mesmo acontece com o potencial elétrico. Considere um sistema que consiste em N cargas\(q_1,q_2,. . ., q_N\). Qual é o potencial elétrico líquido V em um ponto espacial P dessas cargas? Cada uma dessas cargas é uma fonte de carga que produz seu próprio potencial elétrico no ponto P, independente de quaisquer outras mudanças que possam estar fazendo. \(V_1, V_2, . . ., V_N\)Sejam os potenciais elétricos em P produzidos pelas cargas\(q_1,q_2,. . ., q_N\), respectivamente. Então, o potencial elétrico líquido nesse\(V_p\) ponto é igual à soma desses potenciais elétricos individuais. Você pode mostrar isso facilmente calculando a energia potencial de uma carga de teste ao trazer a carga de teste do ponto de referência no infinito para o ponto P:
\[V_p = V_1 + V_2 + . . . + V_N = \sum_1^N V_i.\]
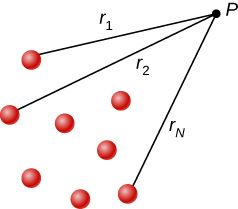
Observe que o potencial elétrico segue o mesmo princípio de superposição do campo elétrico e da energia potencial elétrica. Para mostrar isso de forma mais explícita, observe que uma carga de teste\(q_i\) no ponto P no espaço tem\(r_1,r_2, . . . ,r_N\) distâncias de N cargas fixadas no espaço acima, conforme mostrado na Figura\(\PageIndex{2}\). Usando nossa fórmula para o potencial de uma carga pontual para cada uma dessas cargas (consideradas pontuais), descobrimos que
\[V_p = \sum_1^N k\dfrac{q_i}{r_i} = k\sum_1^N \dfrac{q_i}{r_i}. \label{eq20}\]
Portanto, a energia potencial elétrica da carga de teste é
\[U_p = q_tV_p = q_tk\sum_1^N \dfrac{q_i}{r_i},\]que é o mesmo que o trabalho de trazer a carga de teste para o sistema, conforme encontrado na primeira seção do capítulo.
O dipolo elétrico
Um dipolo elétrico é um sistema de duas cargas iguais, mas opostas, a uma distância fixa. Esse sistema é usado para modelar muitos sistemas do mundo real, incluindo interações atômicas e moleculares. Um desses sistemas é a molécula de água, sob certas circunstâncias. Essas circunstâncias se encontram dentro de um forno de microondas, onde campos elétricos com direções alternadas fazem com que as moléculas de água mudem de orientação. Essa vibração é a mesma que o calor no nível molecular.
Considere o dipolo na Figura\(\PageIndex{3}\) com a magnitude da carga\(q = 3.0 \, \mu C\) e a distância de separação\(d = 4.0 \, cm.\) Qual é o potencial nos seguintes locais no espaço? (a) (0, 0, 1,0 cm); (b) (0, 0, —5,0 cm); (c) (3,0 cm, 0, 2,0 cm).
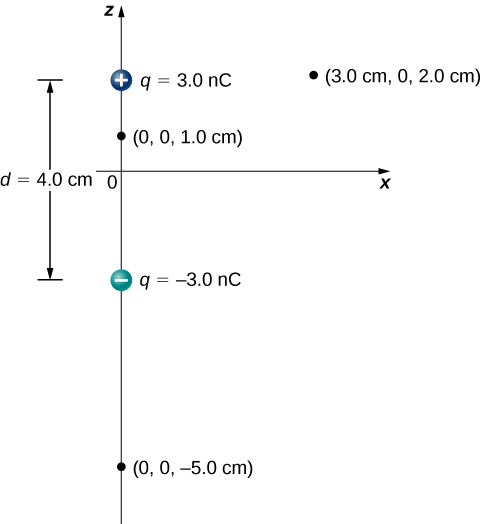
Estratégia
Aplique\(V_p = k \sum_1^N \dfrac{q_i}{r_i}\) a cada um desses três pontos.
Solução
uma.\(V_p = k \sum_1^N \dfrac{q_i}{r_i} = (9.0 \times 10^9 \, N \cdot m^2/C^2) \left(\dfrac{3.0\space nC}{0.010 \, m} - \dfrac{3.0\space nC}{0.030 \, m}\right) = 1.8 \times 10^3 \, V\)
b.\(V_p = k \sum_1^N \dfrac{q_i}{r_i} = (9.0 \times 10^9 \, N \cdot m^2/C^2) \left(\dfrac{3.0\space nC}{0.070 \, m} - \dfrac{3.0\space nC}{0.030 \, m}\right) = -5.1 \times 10^2 \, V\)
c.\(V_p = k \sum_1^N \dfrac{q_i}{r_i} = (9.0 \times 10^9 \, N \cdot m^2/C^2) \left(\dfrac{3.0\space nC}{0.030 \, m} - \dfrac{3.0\space nC}{0.050 \, m}\right) = 3.6 \times 10^2 \, V\)
Significância
Observe que avaliar o potencial é significativamente mais simples do que o campo elétrico, devido ao potencial ser um escalar em vez de um vetor.
Qual é o potencial no eixo x? O eixo z
Solução
No eixo x, o potencial é zero, devido às cargas iguais e opostas à mesma distância dele. No eixo z, podemos sobrepor os dois potenciais; descobriremos que\(z > > d\), novamente, o potencial vai para zero devido ao cancelamento.
Agora, vamos considerar o caso especial em que a distância do ponto P do dipolo é muito maior do que a distância entre as cargas no dipolo\(r >> d\); por exemplo, quando estamos interessados no potencial elétrico devido a uma molécula polarizada, como uma molécula de água. Não é tão longe (infinito) que possamos simplesmente tratar o potencial como zero, mas a distância é grande o suficiente para que possamos simplificar nossos cálculos em relação ao exemplo anterior.
Começamos observando que na Figura\(\PageIndex{4}\) o potencial é dado por
\[V_p = V_+ + V_- = k \left( \dfrac{q}{r_+} - \dfrac{q}{r_-} \right)\]
onde
\[r_{\pm} = \sqrt{x^2 + \left(z \pm \dfrac{d}{2}\right)^2}.\]
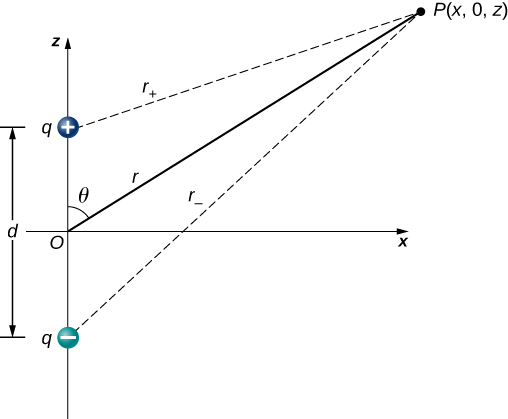
Essa ainda é a fórmula exata. Para aproveitar o fato de que\(r \gg d\), reescrevemos os raios em termos de coordenadas polares, com\(x = r \, \sin \, \theta\) e z = r\,\ cos\,\ theta\). Isso nos dá
\[r_{\pm} = \sqrt{r^2 \, \sin^2 \, \theta + \left(r \, \cos \, \theta \pm \dfrac{d}{2} \right)^2}.\]
Podemos simplificar essa expressão retirando r da raiz,
\[r_{\pm} = \sqrt{\sin^2 \, \theta + \left(r \, \cos \, \theta \pm \dfrac{d}{2} \right)^2}\]
e depois multiplicando os parênteses
\[r_{\pm} = r \sqrt{\sin^2\space \theta + \cos^2 \, \theta \pm \cos \, \theta\dfrac{d}{r} + \left(\dfrac{d}{2r}\right)^2} = r\sqrt{1 \pm \cos \, \theta \dfrac{d}{r} + \left(\dfrac{d}{2r}\right)^2}.\]
O último termo na raiz é pequeno o suficiente para ser insignificante (lembre-se e\(r >> d\), portanto,\((d/r)^2\) é extremamente pequeno, efetivamente zero ao nível que provavelmente mediremos), deixando-nos com
\[r_{\pm} = r\sqrt{1 \pm \cos \, \theta \dfrac{d}{r}}.\]
Usando a aproximação binomial (um resultado padrão da matemática de séries, quando\(a\) é pequeno)
\[\dfrac{1}{\sqrt{1 \pm a}} \approx 1 \pm \dfrac{a}{2}\]
e substituindo isso em nossa fórmula por\(V_p\), obtemos
\[V_p = k\left[\dfrac{q}{r}\left(1 + \dfrac{d \, \cos \, \theta}{2r} \right) - \dfrac{q}{r}\left(1 - \dfrac{d \, \cos \, \theta}{2r}\right)\right] = k\dfrac{qd \, \cos \theta}{r^2}.\]
Isso pode ser escrito de forma mais conveniente se definirmos uma nova quantidade, o momento de dipolo elétrico,
\[\vec{p} = q\vec{d},\]
onde esses vetores apontam da carga negativa para a positiva. Observe que isso tem magnitude qd. Essa quantidade nos permite escrever o potencial no ponto P devido a um dipolo na origem como
\[V_p = k\dfrac{\vec{p} \cdot \hat{r}}{r^2}.\]
Um diagrama da aplicação dessa fórmula é mostrado na Figura\(\PageIndex{5}\).
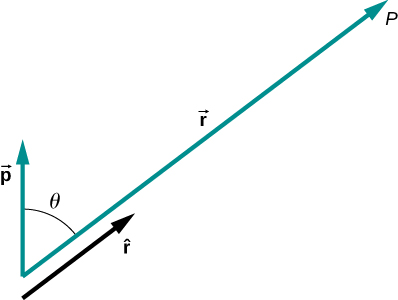
Também há momentos de ordem superior, para quadrupolos, octupolos e assim por diante. Você os verá em aulas futuras.
Potencial da distribuição contínua de cargas
Temos trabalhado muito com cobranças pontuais, mas e quanto às distribuições contínuas de cobranças? Recorde da Equação\ ref {eq20} que
\[V_p = k\sum \dfrac{q_i}{r_i}.\]
Podemos tratar uma distribuição contínua de carga como uma coleção de pontos individuais separados infinitesimalmente. Isso produz a integral
\[V_p = \int \dfrac{dq}{r}\]
para o potencial em um ponto P. Observe que\(r\) é a distância de cada ponto individual na distribuição de carga até o ponto P. Como vimos em Cargas e Campos Elétricos, as cargas infinitesimais são dadas por
\[\underbrace{dq = \lambda \, dl}_{one \, dimension}\]
\[\underbrace{dq = \sigma \, dA}_{two \, dimensions}\]
\[\underbrace{dq = \rho \, dV \space}_{three \, dimensions}\]
onde\(\lambda\) é a densidade de carga linear,\(\sigma\) é a carga por unidade de área e\(\rho\) é a carga por unidade de volume.
Encontre o potencial elétrico de um fio não condutor de carga uniforme com densidade linear\(\lambda\) (coulomb/metro) e comprimento L em um ponto que fica em uma linha que divide o fio em duas partes iguais.
Estratégia
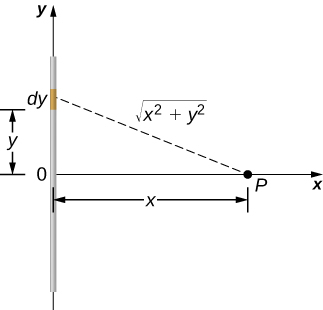
Para configurar o problema, escolhemos as coordenadas cartesianas de forma a explorar a simetria do problema o máximo possível. Colocamos a origem no centro do fio e orientamos o eixo y ao longo do fio de forma que as extremidades do fio fiquem em\(y = \pm L/2\). O ponto de campo P está no plano xy e, como a escolha dos eixos depende de nós, escolhemos o eixo x para passar pelo ponto de campo P, conforme mostrado na Figura\(\PageIndex{6}\).
Solução
Considere um pequeno elemento da distribuição de carga entre y\(y + dy\) e. A carga nessa célula é\(dq = \lambda \, dy\) e a distância da célula até o ponto de campo P é\(\sqrt{x^2 + y^2}\). Portanto, o potencial se torna
\[\begin{align} V_p &= k \int \dfrac{dq}{r} \nonumber \\[4pt] &= k\int_{-L/2}^{L/2} \dfrac{\lambda \, dy}{\sqrt{x^2 + y^2}} \nonumber \\[4pt] &= k\lambda \left[ln \left(y + \sqrt{y^2 + x^2}\right) \right]_{-L/2}^{L/2} \nonumber \\[4pt] &= k\lambda \left[ ln \left(\left(\dfrac{L}{2}\right) + \sqrt{\left(\dfrac{L}{2}\right)^2 + x^2}\right) - ln\left(\left(-\dfrac{L}{2}\right) + \sqrt{\left(-\dfrac{L}{2}\right)^2 + x^2}\right)\right] \nonumber \\[4pt] &= k\lambda ln \left[ \dfrac{L + \sqrt{L^2 + 4x^2}}{-L + \sqrt{L^2 + 4x^2}}\right]. \nonumber \end{align} \nonumber\]
Significância
Observe que isso foi mais simples do que o problema equivalente para o campo elétrico, devido ao uso de quantidades escalares. Lembre-se de que esperamos que o nível zero do potencial esteja no infinito, quando temos uma carga finita. Para examinar isso, tomamos o limite do potencial acima quando x se aproxima do infinito; nesse caso, os termos dentro do log natural se aproximam de um e, portanto, o potencial se aproxima de zero nesse limite. Observe que poderíamos ter feito esse problema de forma equivalente em coordenadas cilíndricas; o único efeito seria substituir r por x e z por y.
Um anel tem uma densidade de carga uniforme\(\lambda\), com unidades de coulomb por unidade de metro de arco. Encontre o potencial elétrico em um ponto do eixo que passa pelo centro do anel.
Estratégia
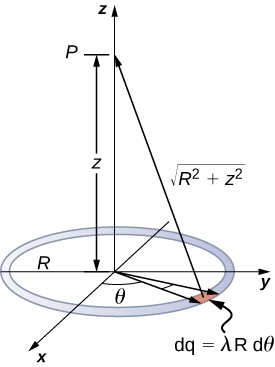
Usamos o mesmo procedimento do fio carregado. A diferença aqui é que a carga é distribuída em um círculo. Dividimos o círculo em elementos infinitesimais em forma de arcos no círculo e usamos as coordenadas cilíndricas mostradas na Figura\(\PageIndex{7}\).
Solução
Um elemento geral do arco entre\(\theta\) e\(\theta + d\theta\) é de comprimento\(Rd\theta\) e, portanto, contém uma carga igual\(\lambda Rd\theta\) a. O elemento está a uma distância\(\sqrt{z^2 + R^2}\) de P e, portanto, o potencial é
\[\begin{align} V_p &= k\int \dfrac{dq}{r} \nonumber \\[4pt] &= k \int_0^{2\pi} \dfrac{\lambda Rd\theta}{\sqrt{z^2 + R^2}} \nonumber \\[4pt] &= \dfrac{k \lambda R}{\sqrt{z^2 + R^2}} \int_0^{2\pi} d\theta \nonumber \\[4pt] &= \dfrac{2\pi k \lambda R}{\sqrt{z^2 + R^2}} \nonumber \\[4pt] &= k \dfrac{q_{tot}}{\sqrt{z^2 + R^2}}. \nonumber \end{align} \nonumber\]
Significância
Esse resultado é esperado porque cada elemento do anel está à mesma distância do ponto P. O potencial líquido em P é o da carga total colocada à distância comum,\(\sqrt{z^2 + R^2}\).
Um disco de raio R tem uma densidade de carga uniforme\(\sigma\) com unidades de coulomb por metro quadrado. Encontre o potencial elétrico em qualquer ponto do eixo que passa pelo centro do disco.
Estratégia
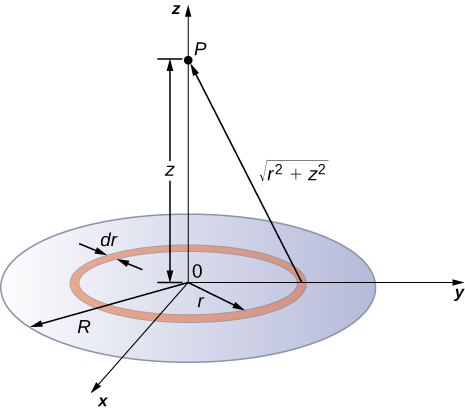
Dividimos o disco em células em forma de anel e usamos o resultado de um anel elaborado no exemplo anterior e, em seguida, integramos sobre r além de\(\theta\). Isso é mostrado na Figura\(\PageIndex{8}\).
Solução
Uma célula de largura infinitesimal entre as coordenadas cilíndricas r e\(r + dr\) mostrada na Figura\(\PageIndex{8}\) será um anel de cargas cujo potencial elétrico\(dV_p\) no ponto de campo tem a seguinte expressão
\[dV_p = k \dfrac{dq}{\sqrt{z^2 + r^2}}\]
onde
\[dq = \sigma 2\pi r dr.\]
A superposição do potencial de todos os anéis infinitesimais que compõem o disco fornece o potencial líquido no ponto P. Isso é feito integrando de\(r = 0\) para\(r = R\):
\[\begin{align} V_p &= \int dV_p = k2\pi \sigma \int_0^R \dfrac{r \, dr}{\sqrt{z^2 + r^2}}, \nonumber \\[4pt] &= k2\pi \sigma ( \sqrt{z^2 + R^2} - \sqrt{z^2}).\nonumber \end{align} \nonumber\]
Significância
O procedimento básico para um disco é primeiro integrar em torno de θ e depois em r. Isso foi demonstrado para uma densidade de carga uniforme (constante). Freqüentemente, a densidade de carga varia com r e, em seguida, a última integral fornecerá resultados diferentes.
Encontre o potencial elétrico devido a um fio infinitamente longo e uniformemente carregado.
Estratégia
Como já calculamos o potencial de um fio finito de comprimento L em Exemplo\(\PageIndex{4}\), podemos nos perguntar se\(L \rightarrow \infty\) o resultado anterior funcionará:
\[V_p = \lim_{L \rightarrow \infty} k \lambda \ln \left(\dfrac{L + \sqrt{L^2 + 4x^2}}{-L + \sqrt{L^2 + 4x^2}}\right).\]
No entanto, esse limite não existe porque o argumento do logaritmo se torna [2/0] as\(L \rightarrow \infty\), então essa maneira de encontrar V de um fio infinito não funciona. A razão para esse problema pode ser atribuída ao fato de que as cargas não estão localizadas em algum espaço, mas continuam infinitas na direção do fio. Portanto, nossa suposição (tácita) de que o potencial zero deve estar a uma distância infinita do fio não é mais válida.
Para evitar essa dificuldade no cálculo de limites, vamos usar a definição de potencial integrando o campo elétrico da seção anterior e o valor do campo elétrico dessa configuração de carga do capítulo anterior.
Solução
Usamos a integral
\[V_p = - \int_R^p \vec{E} \cdot d\vec{l}\]
onde R é uma distância finita da linha de carga, conforme mostrado na Figura\(\PageIndex{9}\).
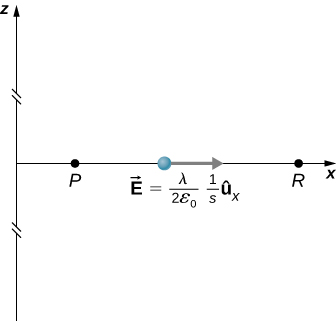
Com essa configuração, usamos\(\vec{E}_p = 2k \lambda \dfrac{1}{s} \hat{s}\) e\(d\vec{l} = d\vec{s}\) para obter
\[\begin{align} V_p - V_R &= - \int_R^p 2k\lambda \dfrac{1}{s}ds \nonumber \\[4pt] &= -2 k \lambda \ln\dfrac{s_p}{s_R}. \nonumber \end{align} \nonumber\]
Agora, se definirmos o potencial de referência\(V_R = 0\) em\(s_R = 1 \, m\), isso simplifica para
\[V_p = -2 k\lambda \, \ln \, s_p.\]
Observe que essa forma do potencial é bastante utilizável; é 0 a 1 m e é indefinida no infinito, por isso não poderíamos usar a última como referência.
Significância
Embora calcular o potencial diretamente possa ser bastante conveniente, acabamos de encontrar um sistema para o qual essa estratégia não funciona bem. Nesses casos, voltar à definição de potencial em termos de campo elétrico pode oferecer um caminho a seguir.
Qual é o potencial no eixo de um anel de carga não uniforme, onde está a densidade de carga\(\lambda (\theta) = \lambda \, \cos \, \theta\)?
Solução
Será zero, pois em todos os pontos do eixo, existem cargas iguais e opostas equidistantes do ponto de interesse. Observe que essa distribuição, de fato, terá um momento de dipolo.


