7.3: Potencial elétrico e diferença de potencial
- Page ID
- 184824
Ao final desta seção, você poderá:
- Defina potencial elétrico, tensão e diferença de potencial
- Defina o elétron-volt
- Calcule o potencial elétrico e a diferença de potencial da energia potencial e do campo elétrico
- Descreva sistemas nos quais o elétron-volt é uma unidade útil
- Aplique a conservação de energia em sistemas elétricos
Lembre-se de que anteriormente definimos o campo elétrico como uma quantidade independente da carga de teste em um determinado sistema, o que, no entanto, nos permitiria calcular a força que resultaria em uma carga de teste arbitrária. (A suposição padrão na ausência de outras informações é que a carga do teste é positiva.) Definimos brevemente um campo para a gravidade, mas a gravidade é sempre atraente, enquanto a força elétrica pode ser atraente ou repulsiva. Portanto, embora a energia potencial seja perfeitamente adequada em um sistema gravitacional, é conveniente definir uma quantidade que nos permita calcular o trabalho com uma carga independente da magnitude da carga. Calcular o trabalho diretamente pode ser difícil, pois\(W = \vec{F} \cdot \vec{d}\) a direção e a magnitude de\(\vec{F}\) podem ser complexas para várias cargas, para objetos de formatos estranhos e ao longo de caminhos arbitrários. Mas sabemos disso porque\(\vec{F}\) o trabalho e, portanto,\(\Delta U\) é proporcional à carga do teste\(q\). Para ter uma quantidade física independente da carga de teste, definimos potencial elétrico\(V\) (ou simplesmente potencial, já que se entende elétrico) como a energia potencial por unidade de carga:
A energia potencial elétrica por unidade de carga é
\[V = \dfrac{U}{q}. \label{eq-1}\]
Como U é proporcional a q, a dependência de q é cancelada. Assim, V não depende de q. A mudança na energia potencial\(\Delta U\) é crucial, então estamos preocupados com a diferença de potencial ou potencial\(\Delta V\) entre dois pontos, onde
A diferença de potencial elétrico entre os pontos A e B\(V_B - V_A\) é definida como a mudança na energia potencial de uma carga q movida de A para B, dividida pela carga. As unidades de diferença de potencial são joules por coulomb, dado o nome de volt (V) em homenagem a Alessandro Volta.
\[1 \, V = 1 \, J/C \label{eq0}\]
O termo familiar voltagem é o nome comum para diferença de potencial elétrico. Lembre-se de que sempre que uma tensão é cotada, ela é entendida como a diferença de potencial entre dois pontos. Por exemplo, cada bateria tem dois terminais e sua voltagem é a diferença de potencial entre eles. Mais fundamentalmente, o ponto que você escolhe para ser zero volts é arbitrário. Isso é análogo ao fato de que a energia potencial gravitacional tem um zero arbitrário, como o nível do mar ou talvez o chão de uma sala de aula. Vale a pena enfatizar a distinção entre diferença de potencial e energia potencial elétrica.
A relação entre diferença de potencial (ou tensão) e energia potencial elétrica é dada por
\[\Delta V = \dfrac{\Delta U}{q} \label{eq1}\]
ou
\[ \Delta U = q \Delta V. \label{eq2}\]
A voltagem não é o mesmo que energia. A tensão é a energia por unidade de carga. Assim, uma bateria de motocicleta e uma bateria de carro podem ter a mesma voltagem (mais precisamente, a mesma diferença de potencial entre os terminais da bateria), mas uma armazena muito mais energia do que a outra porque\(\Delta U = q\Delta V\). A bateria do carro pode mover mais carga do que a bateria da motocicleta, embora ambas sejam baterias de 12 V.
Você tem uma bateria de motocicleta de 12,0 V que pode mover 5000 C de carga e uma bateria de carro de 12,0 V que pode mover 60.000 C de carga. Quanta energia cada um fornece? (Suponha que o valor numérico de cada carga seja preciso em três algarismos significativos.)
Estratégia
Dizer que temos uma bateria de 12,0 V significa que seus terminais têm uma diferença de potencial de 12,0 V. Quando essa bateria move a carga, ela coloca a carga em uma diferença de potencial de 12,0 V, e a carga recebe uma mudança na energia potencial igual\(\Delta U = q\Delta V\) a. Para encontrar a saída de energia, multiplicamos a carga movida pela diferença de potencial.
Solução
Para a bateria da motocicleta,\(q = 5000 \, C\)\(\Delta V = 12.0 \, V\) e. A energia total fornecida pela bateria da motocicleta é
\[\Delta U_{cycle} = (5000 \, C)(12.0 \, V) = (5000 \, C)(12.0 \, J/C) = 6.00 \times 10^4 \, J. \nonumber\]
Da mesma forma, para a bateria do carro\(q = 60,000 \, C\) e
\[\Delta U_{car} = (60,000 \, C)(12.0 \, V) = 7.20 \times 10^5 \, J. \nonumber\]
Significância
A tensão e a energia estão relacionadas, mas não são a mesma coisa. As voltagens das baterias são idênticas, mas a energia fornecida por cada uma é bem diferente. A bateria de um carro tem um motor muito maior para dar partida do que uma motocicleta. Observe também que, quando a bateria é descarregada, parte de sua energia é usada internamente e a tensão do terminal diminui, como quando os faróis se apagam devido a uma bateria de carro esgotada. A energia fornecida pela bateria ainda é calculada como neste exemplo, mas nem toda a energia está disponível para uso externo.
Quanta energia uma bateria AAA de 1,5 V tem que pode mover 100° C?
- Resposta
-
\(\Delta U = q\Delta V = (100 \, C)(1.5 \, V) = 150 \, J\)
Observe que as energias calculadas no exemplo anterior são valores absolutos. A mudança na energia potencial da bateria é negativa, pois ela perde energia. Essas baterias, como muitos sistemas elétricos, na verdade movem cargas negativas — elétrons em particular. As baterias repelem elétrons de seus terminais negativos (A) através de qualquer circuito envolvido e os atraem para seus terminais positivos (B), conforme mostrado na Figura\(\PageIndex{1}\). A mudança no potencial é\(\Delta V = V_B - V_A = +12 \, V\) e a carga q é negativa, então isso\(\Delta U = q \Delta V\) é negativo, o que significa que a energia potencial da bateria diminuiu quando q passou de A para B.
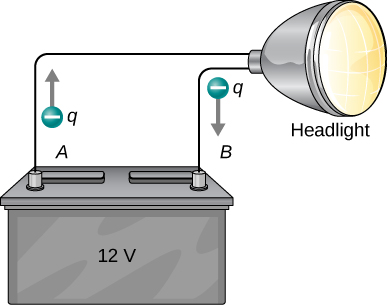
Quando uma bateria de carro de 12,0 V alimenta um único farol de 30,0 W, quantos elétrons passam por ele a cada segundo?
Estratégia
Para encontrar o número de elétrons, precisamos primeiro encontrar a carga que se move em 1,00 s. A carga movida está relacionada à tensão e energia por meio das equações\(\Delta U = q \Delta V\). Uma lâmpada de 30,0 W usa 30,0 joules por segundo. Como a bateria perde energia, nós temos\(\Delta U = - 30 \, J\) e, como os elétrons estão indo do terminal negativo para o positivo, vemos isso\(\Delta V = +12.0 \, V\).
Solução
Para encontrar a carga que q moveu, resolvemos a equação\(\Delta U = q\Delta V\):
\[q = \dfrac{\Delta U}{\Delta V}.\]
Inserindo os valores para\(\Delta U\) e\(\Delta V\), obtemos
\[q = \dfrac{-30.0 \, J}{+12.0 \, V} = \dfrac{-30.0 \, J}{+12.0 \, J/C} = -2.50 \, C.\]
O número de elétrons\(n_e\) é a carga total dividida pela carga por elétron. Ou seja,
\[n_e = \dfrac{-2.50 \, C}{-1.60 \times 10^{-19} C/e^-} = 1.56 \times 10^{19} \, electrons.\]
Significância
Esse é um número muito grande. Não é de admirar que normalmente não observemos elétrons individuais com tantos presentes em sistemas comuns. De fato, a eletricidade estava em uso há muitas décadas antes de ser determinado que as cargas de movimentação em muitas circunstâncias eram negativas. A carga positiva que se move na direção oposta à carga negativa geralmente produz efeitos idênticos; isso torna difícil determinar quem está se movendo ou se ambos estão se movendo.
Quantos elétrons passariam por uma lâmpada de 24,0 W?
- Resposta
-
\(-2.00 \, C, \, n_e = 1.25 \times 10^{19} \, electrons\)
O Electron-Volt
A energia por elétron é muito pequena em situações macroscópicas como a do exemplo anterior — uma pequena fração de um joule. Mas em uma escala submicroscópica, essa energia por partícula (elétron, próton ou íon) pode ser de grande importância. Por exemplo, mesmo uma pequena fração de um joule pode ser grande o suficiente para que essas partículas destruam moléculas orgânicas e danifiquem tecidos vivos. A partícula pode causar danos por colisão direta ou criar raios X prejudiciais, que também podem causar danos. É útil ter uma unidade de energia relacionada aos efeitos submicroscópicos.
A figura\(\PageIndex{2}\) mostra uma situação relacionada à definição de tal unidade de energia. Um elétron é acelerado entre duas placas de metal carregadas, como pode ser em um modelo antigo de tubo de televisão ou osciloscópio. O elétron ganha energia cinética que depois é convertida em outra forma — luz no tubo da televisão, por exemplo. (Observe que, em termos de energia, “ladeira abaixo” para o elétron é “subida” para uma carga positiva.) Como a energia está relacionada à voltagem por\(\Delta U = q\Delta V\), podemos pensar no joule como um coulomb-volt.
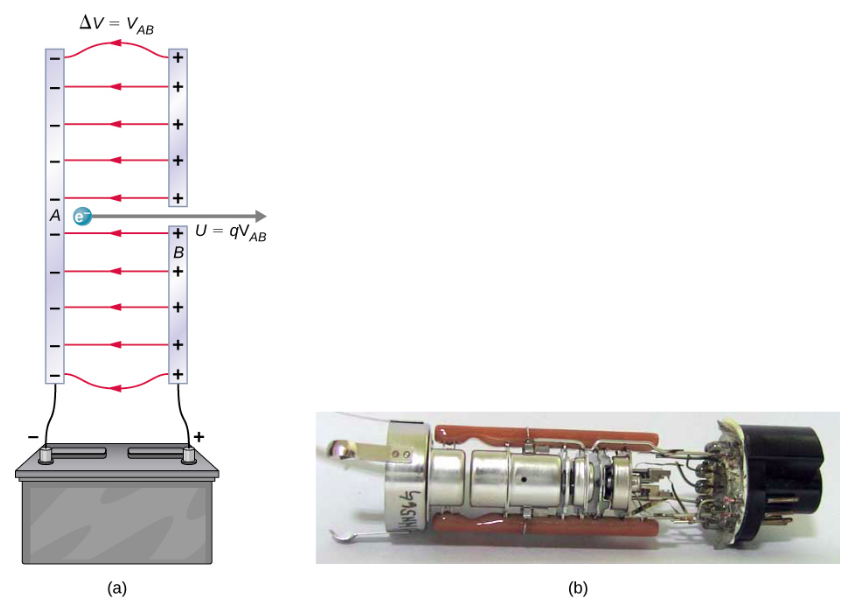
Na escala submicroscópica, é mais conveniente definir uma unidade de energia chamada elétron-volt (eV), que é a energia dada a uma carga fundamental acelerada por meio de uma diferença de potencial de 1 V. Na forma de equação,
\[1 \, eV = (1.60 \times 10^{-19} C)(1 \, V) = (1.60 \times 10^{-19} C)(1 \, J/C) = 1.60 \times 10^{-19} \, J.\]
Um elétron acelerado através de uma diferença de potencial de 1 V recebe uma energia de 1 eV. Conclui-se que um elétron acelerado através de 50 V ganha 50 eV. Uma diferença de potencial de 100.000 V (100 kV) dá a um elétron uma energia de 100.000 eV (100 keV) e assim por diante. Da mesma forma, um íon com uma carga positiva dupla acelerada em 100 V ganha 200 eV de energia. Essas relações simples entre tensão acelerada e cargas de partículas tornam o elétron-volt uma unidade de energia simples e conveniente em tais circunstâncias.
O elétron-volt é comumente empregado em processos submicroscópicos - as energias de valência química e as energias de ligação molecular e nuclear estão entre as quantidades frequentemente expressas em elétron-volts. Por exemplo, são necessários cerca de 5 eV de energia para quebrar certas moléculas orgânicas. Se um próton for acelerado do repouso por meio de uma diferença de potencial de 30 kV, ele adquire uma energia de 30 keV (30.000 eV) e pode quebrar até 6000 dessas moléculas\((30,000 \, eV \, : \, 5 \, eV \, per \, molecule = 6000 \, molecules)\). As energias de decaimento nuclear são da ordem de 1 MeV (1.000.000 eV) por evento e, portanto, podem produzir danos biológicos significativos.
Conservação de energia
A energia total de um sistema é conservada se não houver adição (ou subtração) líquida devido ao trabalho ou à transferência de calor. Para forças conservadoras, como a força eletrostática, a conservação da energia afirma que a energia mecânica é uma constante.
A energia mecânica é a soma da energia cinética e da energia potencial de um sistema; isto é,\(K + U = constant\). A perda de U para uma partícula carregada se torna um aumento em seu K. A conservação de energia é declarada em forma de equação como
\[K + U = constant\]ou\[K_i + U_i = K_f + U_f\]
onde i e f representam as condições iniciais e finais. Como descobrimos muitas vezes antes, considerar a energia pode nos dar uma ideia e facilitar a solução de problemas.
Calcule a velocidade final de um elétron livre acelerado do repouso por meio de uma diferença de potencial de 100 V. (Suponha que esse valor numérico seja preciso para três dígitos significativos).
Estratégia
Temos um sistema com apenas forças conservadoras. Supondo que o elétron seja acelerado no vácuo e negligenciando a força gravitacional (verificaremos essa suposição posteriormente), toda a energia potencial elétrica é convertida em energia cinética. Podemos identificar as formas inicial e final de energia a ser
\(K_i = 0\),\(K_f = \frac{1}{2}mv^2\),\(U_i = qV\),\(U_f = 0\).
Solução
A conservação de energia afirma que
\[K_i + U_i = K_f + U_f.\]
Inserindo os formulários identificados acima, obtemos
\[qV = \dfrac{mv^2}{2}.\]
Resolvemos isso para v:
\[v = \sqrt{\dfrac{2qV}{m}}.\]
Ao inserir valores para q, V e m, obtém-se
\[v = \sqrt{\dfrac{2(-1.60 \times 10^{-19}C)(-100 \, J/C)}{9.11 \times 10^{-31} kg}} = 5.93 \times 10^6 \, m/s.\]
Significância
Observe que tanto a carga quanto a tensão inicial são negativas, como na Figura\(\PageIndex{2}\). A partir da discussão sobre carga elétrica e campo elétrico, sabemos que as forças eletrostáticas em partículas pequenas são geralmente muito grandes em comparação com a força gravitacional. A grande velocidade final confirma que a força gravitacional é realmente insignificante aqui. A grande velocidade também indica como é fácil acelerar elétrons com voltagens pequenas devido à sua massa muito pequena. Tensões muito maiores do que 100 V neste problema são normalmente usadas em pistolas de elétrons. Essas tensões mais altas produzem velocidades de elétrons tão grandes que os efeitos da relatividade especial devem ser levados em consideração e serão discutidos em outro lugar. É por isso que consideramos uma baixa voltagem (com precisão) neste exemplo.
Como esse exemplo mudaria com um pósitron? Um pósitron é idêntico a um elétron, exceto que a carga é positiva.
- Resposta
-
Estaria indo na direção oposta, sem nenhum efeito nos cálculos apresentados.
Tensão e campo elétrico
Até agora, exploramos a relação entre tensão e energia. Agora, queremos explorar a relação entre tensão e campo elétrico. Começaremos com o caso geral de um\(\vec{E}\) campo não uniforme. Lembre-se de que nossa fórmula geral para a energia potencial de uma carga de teste q no ponto P em relação ao ponto de referência R é
\[U_p = - \int_R^p \vec{F} \cdot d\vec{l}.\]
Quando substituímos a definição de campo elétrico\((\vec{E} = \vec{F}/q)\), isso se torna
\[U_p = -q \int_R^p \vec{E} \cdot d\vec{l}.\]
Aplicando nossa definição de potencial\((V = U/q)\) a essa energia potencial, descobrimos que, em geral,
\[V_p = - \int_R^p \vec{E} \cdot d\vec{l}.\]
De nossa discussão anterior sobre a energia potencial de uma carga em um campo elétrico, o resultado é independente do caminho escolhido e, portanto, podemos escolher o caminho integral mais conveniente.
Considere o caso especial de uma carga pontual positiva q na origem. Para calcular o potencial causado por q a uma distância r da origem em relação a uma referência de 0 no infinito (lembre-se de que fizemos o mesmo com a energia potencial), deixe\(P = r\) e\(R = \infty\), com\(d\vec{l} = d\vec{r} = \hat{r}dr\) e use\(\vec{E} = \frac{kq}{r^2} \hat{r}\). Quando avaliamos a integral
\[V_p = - \int_R^p \vec{E} \cdot d\vec{l}\]para este sistema, temos
\[V_r = - \int_{\infty}^r \dfrac{kq}{r^2} dr = \dfrac{kq}{r} - \dfrac{kq}{\infty} = \dfrac{kq}{r}.\]
Esse resultado,
\[V_r = \dfrac{kq}{r}\]
é a forma padrão do potencial de uma carga pontual. Isso será explorado mais detalhadamente na próxima seção.
Para examinar outro caso especial interessante, suponha que um campo elétrico uniforme\(\vec{E}\) seja produzido colocando uma diferença de potencial (ou tensão)\(\Delta V\) em duas placas de metal paralelas, rotuladas A e B (Figura\(\PageIndex{3}\)). O exame dessa situação nos dirá qual voltagem é necessária para produzir uma certa intensidade de campo elétrico. Também revelará uma relação mais fundamental entre potencial elétrico e campo elétrico.
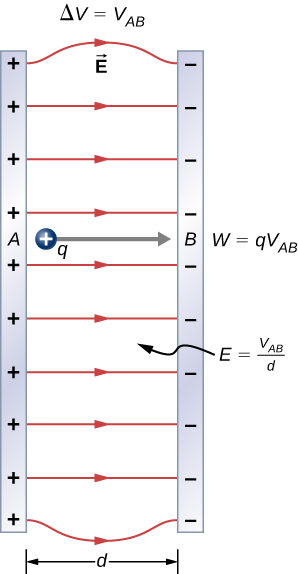
Do ponto de vista de um físico,\(\vec{E}\) pode\(\Delta V\) ou pode ser usado para descrever qualquer interação entre cargas. No entanto,\(\Delta V\) é uma quantidade escalar e não tem direção, enquanto\(\vec{E}\) é uma grandeza vetorial, com magnitude e direção. (Observe que a magnitude do campo elétrico, uma quantidade escalar, é representada por E.) A relação entre\(\Delta V\) e\(\vec{E}\) é revelada pelo cálculo do trabalho realizado pela força elétrica ao mover uma carga do ponto A para o ponto B. Mas, conforme observado anteriormente, as distribuições arbitrárias de cargas exigem cálculo. Portanto, consideramos um campo elétrico uniforme como um caso especial interessante.
O trabalho realizado pelo campo elétrico na Figura\(\PageIndex{3}\) para mover uma carga positiva q de A, a placa positiva, maior potencial, para B, a placa negativa, menor potencial, é
\[W = - \Delta U = - q\Delta V.\]
A diferença de potencial entre os pontos A e B é
\[- \Delta V = - (V_B - V_A) = V_A - V_B = V_{AB}.\]
Inserir isso na expressão de trabalho rende
\[W = qV_{AB}.\]
O trabalho é\(W = \vec{F} \cdot \vec{d} = Fd \, cos \, \theta\): aqui\(cos \, \theta = 1\), já que o caminho é paralelo ao campo. Assim,\(W = Fd\). Já\(F = qE\) que vemos isso\(W = qEd\).
Substituindo essa expressão por trabalho na equação anterior, obtém-se:
\[qEd = qV_{AB}.\]
A carga é cancelada, então obtemos a tensão entre os pontos A e B.
Somente no campo E uniforme:\[V_{AB} = Ed\]\[E = \dfrac{V_{AB}}{d}\] onde d é a distância de A a B, ou a distância entre as placas na Figura\(\PageIndex{3}\). Observe que essa equação implica que as unidades de campo elétrico são volts por metro. Já sabemos que as unidades de campo elétrico são newtons por coulomb; portanto, a seguinte relação entre unidades é válida:
\[1 \, N/C = 1 \, V/m.\]
Além disso, podemos estender isso para a forma integral. Substituindo a Equação\ ref {eq1} em nossa definição pela diferença de potencial entre os pontos A e B, obtemos
\[V_{AB} = V_B - V_A = - \int_R^B \vec{E} \cdot d\vec{l} + \int_R^A \vec{E} \cdot d\vec{l}\]
o que simplifica para
\[V_B - V_A = - \int_A^B \vec{E} \cdot d\vec{l}.\]
Como demonstração, a partir disso, podemos calcular a diferença de potencial entre dois pontos (A e B) eqüidistantes de uma carga pontual q na origem, conforme mostrado na Figura\(\PageIndex{4}\).
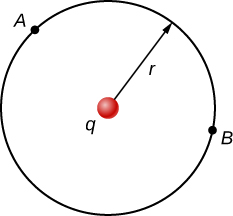
Para fazer isso, integramos em torno de um arco do círculo de raio constante r entre A e B, o que significa que deixamos\(d\vec{l} = r\hat{\varphi}d\varphi\), enquanto usamos\(\vec{E} = \frac{kq}{r^2} \hat{r}\). Assim,
\[\Delta V = V_B - V_A = - \int_A^B \vec{E} \cdot d\vec{l}.\]
pois este sistema se torna
\[V_B - V_A = - \int_A^B \frac{kq}{r^2} \cdot r\hat{\varphi}d\varphi.\]
No entanto,\(\hat{r} \cdot \hat{\varphi}\) e portanto
\[V_B - V_A = 0.\]
Esse resultado, de que não há diferença de potencial ao longo de um raio constante a partir de uma carga pontual, será útil quando mapearmos potenciais.
O ar seco pode suportar uma intensidade máxima de campo elétrico de aproximadamente\(3.0 \times 10^6 V/m\). Acima desse valor, o campo cria ionização suficiente no ar para tornar o ar um condutor. Isso permite uma descarga ou faísca que reduz o campo. Qual é, então, a tensão máxima entre duas placas condutoras paralelas separadas por 2,5 cm de ar seco?
Estratégia
Recebemos o campo elétrico máximo E entre as placas e a distância d entre elas. Podemos usar a equação\(V_{AB} = Ed\) para calcular a tensão máxima.
Solução
A diferença de potencial ou tensão entre as placas é
\[V_{AB} = Ed.\]
Inserindo os valores fornecidos para E e d dá
\[V_{AB} = (3.0 \times 10^6 V/m)(0.025 \, m) = 7.5 \times 10^4 \, V\]ou\[V_{AB} = 75 \, kV.\]
(A resposta é citada com apenas dois dígitos, já que a intensidade máxima do campo é aproximada.)
Significância
Uma das implicações desse resultado é que são necessários cerca de 75 kV para fazer uma faísca saltar através de uma lacuna de 2,5 cm (1 pol.) ou 150 kV para uma faísca de 5 cm. Isso limita as tensões que podem existir entre os condutores, talvez em uma linha de transmissão de energia. Uma voltagem menor pode causar faíscas se houver espinhos na superfície, pois pontos afiados têm maior intensidade de campo do que superfícies lisas. O ar úmido se decompõe com uma intensidade de campo mais baixa, o que significa que uma voltagem menor fará com que uma faísca salte pelo ar úmido. As maiores tensões podem ser acumuladas com eletricidade estática em dias secos (Figura\(\PageIndex{5}\)).

Um canhão de elétrons (Figura\(\PageIndex{2}\)) tem placas paralelas separadas por 4,00 cm e fornece elétrons 25,0 keV de energia. (a) Qual é a intensidade do campo elétrico entre as placas? (b) Que força esse campo exerceria sobre um pedaço de plástico com uma\(0.500-\mu C\) carga que fica entre as placas?
Estratégia
Como a tensão e a separação da placa são fornecidas, a intensidade do campo elétrico pode ser calculada diretamente da expressão\(E = \frac{V_{AB}}{d}\). Depois de conhecermos a intensidade do campo elétrico, podemos encontrar a força de uma carga usando\(\vec{F} = q\vec{E}\). Como o campo elétrico está em apenas uma direção, podemos escrever essa equação em termos das magnitudes,\(F = qE\).
Solução
a. A expressão para a magnitude do campo elétrico entre duas placas de metal uniformes é
\[E = \dfrac{V_{AB}}{d}.\]Como o elétron é uma carga única e recebe 25,0 keV de energia, a diferença de potencial deve ser 25,0 kV. Inserindo esse valor para\(V_{AB}\) e a separação da placa de 0,0400 m, obtemos\[E = \frac{25.0 \, kV}{0.0400 \, m} = 6.25 \times 10^5 \, V/m.\]
b. A magnitude da força sobre uma carga em um campo elétrico é obtida a partir da equação\[F = qE.\] Substituindo valores conhecidos dá
\[F = (0.500 \times 10^{-6}C)(6.25 \times 10^5 V/m) = 0.313 \, N.\]
Importância Observe que as unidades são newtons, uma vez que\(1 \, V/m = 1 \, N/C\). Como o campo elétrico é uniforme entre as placas, a força na carga é a mesma, não importa onde a carga esteja localizada entre as placas.
Dada uma carga pontual\(q = +2.0-n C\) na origem, calcule a diferença de potencial entre o ponto\(a = 4.0 \, cm\) a\(P_1\) uma distância de q e\(P_2\) uma\(b = 12.0 \, cm\) distância de q, onde os dois pontos têm um ângulo\(\varphi = 24^o\) entre eles (Figura\(\PageIndex{6}\)).
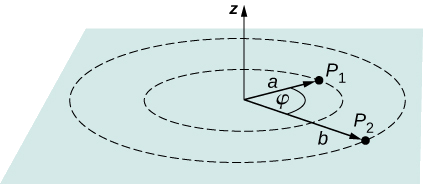
Estratégia Faça isso em duas etapas. O primeiro passo é usar\(V_B - V_A = -\int_A^B \vec{E} \cdot d\vec{l}\) e deixar\(A = a = 4.0 \, cm\) e\(B = b = 12.0 \, cm\), com\(d\vec{l} = d\vec{r} = \hat{r}dr\) e\(\vec{E} = \frac{kq}{r^2} \hat{r}.\) Então executar a integral. O segundo passo é integrar\(V_B - V_A = -\int_A^B \vec{E} \cdot d\vec{l}\) em torno de um arco de raio constante r, o que significa que deixamos\(d\vec{l} = r\vec{\varphi}d\varphi\) com limites\(0 \leq \varphi \leq 24^o\), ainda usando\(\vec{E} = \frac{kq}{r^2}\hat{r}\).
Em seguida, adicione os dois resultados.
Solução Para a primeira parte,\(V_B - V_A = -\int_A^B \vec{E} \cdot d\vec{l}\) pois este sistema se torna\(V_b - V_a = - \int_a^b \frac{kq}{r^2}\hat{r} \cdot \hat{r}dr\) o que computa para
\(\Delta V = - \int_a^b \frac{kq}{r^2}dr = kq \left[\frac{1}{a} - \frac{1}{b}\right]\)
\(= (8.99 \times 10^9 Nm^2/C^2)(2.0 \times 10^{-9}C) \left[\frac{1}{0.040 \, m} - \frac{1}{0.12 \, m}\right] = 300 \, V\).
Para o segundo passo,\(V_B - V_A = -\int_A^B \vec{E} \cdot d\vec{l}\) torna-se\(\Delta V = - \int_{0^o}^{24^o} \frac{kq}{r^2} \hat{r} \cdot r\hat{\varphi}d\varphi\), mas\(\hat{r} \cdot \hat{\varphi} = 0\) e portanto\(\Delta V = 0\). Somando as duas partes, obtemos 300 V.
Significância
Demonstramos o uso da forma integral da diferença de potencial para obter um resultado numérico. Observe que, nesse sistema específico, também poderíamos ter usado a fórmula para o potencial devido a uma carga pontual nos dois pontos e simplesmente calculado a diferença.
A partir dos exemplos, como a energia de um raio varia com a altura das nuvens do solo? Considere o sistema de aterramento em nuvem como duas placas paralelas.
- Resposta
-
Dada uma intensidade máxima fixa de campo elétrico, o potencial em que ocorre um golpe aumenta com o aumento da altura acima do solo. Portanto, cada elétron carregará mais energia. Determinar se há um efeito no número total de elétrons está no futuro.
Antes de apresentar problemas envolvendo eletrostática, sugerimos uma estratégia de resolução de problemas a ser seguida para este tópico.
- Examine a situação para determinar se a eletricidade estática está envolvida; isso pode envolver cargas estacionárias separadas, as forças entre elas e os campos elétricos que elas criam.
- Identifique o sistema de interesse. Isso inclui observar o número, os locais e os tipos de cobranças envolvidas.
- Identifique exatamente o que precisa ser determinado no problema (identifique as incógnitas). Uma lista escrita é útil. Determine se a força de Coulomb deve ser considerada diretamente; nesse caso, pode ser útil desenhar um diagrama de corpo livre usando linhas de campo elétrico.
- Faça uma lista do que é dado ou pode ser inferido do problema conforme declarado (identifique os conhecidos). É importante distinguir a força F de Coulomb do campo elétrico E, por exemplo.
- Resolva a equação apropriada para a quantidade a ser determinada (a desconhecida) ou desenhe as linhas do campo conforme solicitado.
- Examine a resposta para ver se ela é razoável: faz sentido? As unidades estão corretas e os números envolvidos são razoáveis?


