7.2: Energia potencial elétrica
- Page ID
- 184823
Ao final desta seção, você poderá:
- Defina o trabalho realizado por uma força elétrica
- Defina energia potencial elétrica
- Aplique trabalho e energia potencial em sistemas com cargas elétricas
Quando uma carga positiva livre q é acelerada por um campo elétrico, ela recebe energia cinética (Figura\(\PageIndex{1}\)). O processo é análogo a um objeto sendo acelerado por um campo gravitacional, como se a carga estivesse descendo uma colina elétrica onde sua energia potencial elétrica é convertida em energia cinética, embora, é claro, as fontes das forças sejam muito diferentes. Vamos explorar o trabalho realizado em uma carga q pelo campo elétrico nesse processo, para que possamos desenvolver uma definição de energia potencial elétrica.
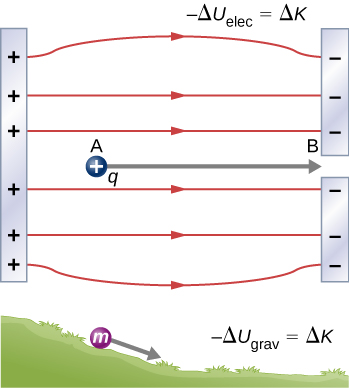
A força eletrostática ou de Coulomb é conservadora, o que significa que o trabalho realizado em q é independente do caminho percorrido, como demonstraremos mais adiante. Isso é exatamente análogo à força gravitacional. Quando uma força é conservadora, é possível definir uma energia potencial associada à força. Geralmente, é mais fácil trabalhar com a energia potencial (porque depende apenas da posição) do que calcular o trabalho diretamente.
Para mostrar isso explicitamente, considere uma carga elétrica\(+q\) fixa na origem e mova outra carga em\(+Q\) direção a q de forma que, a cada instante, a força aplicada equilibre\(\vec{F}\) exatamente a força elétrica\(\vec{F}_e\) em Q (Figura\(\PageIndex{2}\)). O trabalho realizado pela força aplicada\(\vec{F}\) na carga Q altera a energia potencial de Q. Chamamos essa energia potencial de energia potencial elétrica de Q.
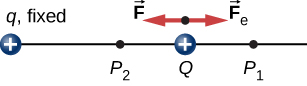
O trabalho\(W_{12}\) realizado pela força aplicada\(\vec{F}\) quando a partícula se move de\(P_1\) para\(P_2\) pode ser calculado por
\[W_{12} = \int_{P_1}^{P_2} \vec{F} \cdot d\vec{l}.\]
Como a força aplicada\(\vec{F}\) equilibra a força elétrica\(\vec{F}_e\) em Q, as duas forças têm a mesma magnitude e direções opostas. Portanto, a força aplicada é
\[\vec{F} = -\vec{F}_e = - \dfrac{kqQ}{r^2} \hat{r},\]
onde definimos positivo como apontando para longe da origem e r é a distância da origem. As direções do deslocamento e da força aplicada no sistema na Figura\(\PageIndex{2}\) são paralelas e, portanto, o trabalho realizado no sistema é positivo.
Usamos a letra U para indicar energia potencial elétrica, que tem unidades de joules (J). Quando uma força conservadora faz um trabalho negativo, o sistema ganha energia potencial. Quando uma força conservadora faz um trabalho positivo, o sistema perde energia potencial\(\Delta U = - W\). No sistema da Figura\(\PageIndex{3}\), a força de Coulomb atua na direção oposta ao deslocamento; portanto, o trabalho é negativo. No entanto, aumentamos a energia potencial no sistema de duas cargas.
Uma\(+3.0-nC\) carga Q está inicialmente em repouso a uma distância de 10 cm (\(r_1\)) de uma\(+5.0-nC\) carga q fixada na origem (Figura\(\PageIndex{3}\)). Naturalmente, a força de Coulomb acelera Q para longe de q, chegando a 15 cm (\(r_2\)).
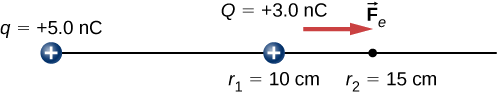
- Qual é o trabalho realizado pelo campo elétrico entre\(r_1\) e\(r_2\)?
- Quanta energia cinética Q tem em\(r_2\)?
Estratégia
Calcule o trabalho com a definição usual. Como Q partiu do repouso, isso é o mesmo que a energia cinética.
Solução
Integrando a força sobre a distância, obtemos
\[\begin{align} W_{12} &= \int_{r_1}^{r_2} \vec{F} \cdot d\vec{r} \nonumber \\[4pt] &= \int_{r_1}^{r_2} \dfrac{kqQ}{r^2}dr \nonumber \\[4pt] &= \left. - \dfrac{kqQ}{r} \right|_{r_1}^{r_2} \nonumber \\[4pt] &= kqQ \left[\dfrac{-1}{r_2} + \dfrac{1}{r_1}\right] \nonumber \\[4pt] &= (8.99 \times 10^9 \, Nm^2/C^2)(5.0 \times 10^{-9} C)(3.0 \times 10^{-9} C) \left[ \dfrac{-1}{0.15 \, m} + \dfrac{1}{0.10 \, m}\right] \nonumber \\[4pt] &= 4.5 \times 10^{-7} \, J. \nonumber \end{align} \nonumber\]
Esse também é o valor da energia cinética em\(r_2\).
Significância
A carga Q estava inicialmente em repouso; o campo elétrico de q funcionou em Q, então agora Q tem energia cinética igual ao trabalho realizado pelo campo elétrico.
Se Q tem uma massa de\(4.00 \, \mu g\), qual é a velocidade de Q em\(r_2\)?
Solução
\(K = \frac{1}{2}mv^2\),\(v = \sqrt{2\frac{K}{m}} = \sqrt{2\frac{4.5 \times 10^{-7}J}{4.00 \times 10^{-9}kg}} = 15 \, m/s.\)
Neste exemplo, o trabalho que W fez para acelerar uma carga positiva do repouso é positivo e resulta de uma perda em U ou negativa\(\Delta U\). Um valor para U pode ser encontrado em qualquer ponto tomando um ponto como referência e calculando o trabalho necessário para mover uma carga para o outro ponto.
O trabalho realizado para acelerar uma carga positiva do repouso é positivo e resulta de uma perda em U ou negativa\(\Delta U\). Matematicamente,
\[W = - \Delta U. \label{7.1}\]
A energia potencial gravitacional e a energia potencial elétrica são bastante análogas. A energia potencial é responsável pelo trabalho realizado por uma força conservadora e fornece uma visão adicional sobre energia e transformação de energia sem a necessidade de lidar diretamente com a força. É muito mais comum, por exemplo, usar o conceito de energia potencial elétrica do que lidar com a força de Coulomb diretamente em aplicações do mundo real.
Em coordenadas polares com q na origem e Q localizado em r, o vetor do elemento de deslocamento é\(d\vec{l} = \hat{r} dr\) e, portanto, o trabalho se torna
\[\begin{align} W_{12} &= kqQ \int_{r_1}^{r_2} \dfrac{1}{r^2} \hat{r} \cdot \hat{r} dr \nonumber \\[4pt] &= \underbrace{kqQ \dfrac{1}{r_2}}_{final \, point} - \underbrace{kqQ \dfrac{1}{r_1}}_{initial \,point}. \end{align}\]
Observe que esse resultado depende apenas dos pontos finais e, de outra forma, é independente do caminho percorrido. Para explorar isso ainda mais, compare\(P_1\) o caminho\(P_2\) com o caminho\(P_1 P_3 P_4 P_2\) na Figura\(\PageIndex{4}\).
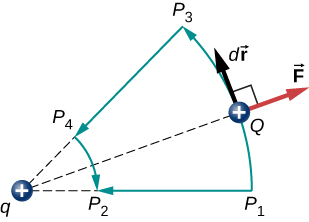
Os segmentos\(P_1P_3\) e\(P_4P_2\) são arcos de círculos centrados em q. Como a força em Q aponta para ou para longe de q, nenhum trabalho é feito por uma força que equilibra a força elétrica, porque ela é perpendicular ao deslocamento ao longo desses arcos. Portanto, o único trabalho realizado é um segmento longo\(P_3P_4\) que é idêntico\(P_1P_2\) a.
Uma implicação desse cálculo de trabalho é que, se contornássemos o caminho\(P_1P_3P_4P_2P_1\), a rede seria zero (Figura\(\PageIndex{5}\)). Lembre-se de que é assim que determinamos se uma força é conservadora ou não. Portanto, como a força elétrica está relacionada ao campo elétrico por\(\vec{F} = g\vec{E}\), o próprio campo elétrico é conservador. Ou seja,
\[\oint \vec{E} \cdot d\vec{l} = 0.\]
Observe que Q é uma constante.

Outra implicação é que podemos definir uma energia potencial elétrica. Lembre-se de que o trabalho realizado por uma força conservadora também é expresso como a diferença na energia potencial correspondente a essa força. Portanto, o trabalho\(W_{ref}\) para levar uma cobrança de um ponto de referência para um ponto de interesse pode ser escrito como
\[W_{ref} = \int_{r_{ref}}^r \vec{F} \cdot d\vec{l}\]
e, pela Equação\ ref {7.1}, a diferença na energia potencial (\(U_2 - U_1\)) da carga de teste Q entre os dois pontos é
\[\Delta U = - \int_{r_{ref}}^r \vec{F} \cdot d\vec{l}.\]
Portanto, podemos escrever uma expressão geral para a energia potencial de cargas de dois pontos (em coordenadas esféricas):
\[\Delta U = - \int_{r_{ref}}^r \dfrac{kqQ}{r^2}dr = -\left[-\dfrac{kqQ}{r}\right]_{r_{ref}}^r = kqQ\left[ \dfrac{1}{r} - \dfrac{1}{r_{ref}}\right].\]
Podemos considerar o segundo termo como um nível de referência constante arbitrário, que serve como referência zero:
\[U(r) = k\dfrac{qQ}{r} - U_{ref}.\]
Uma opção conveniente de referência que se baseia em nosso bom senso é que quando as duas cargas estão infinitamente distantes, não há interação entre elas. (Lembre-se da discussão sobre energia potencial de referência em Energia Potencial e Conservação de Energia.) Tomar a energia potencial desse estado como zero remove o termo\(U_{ref}\) da equação (assim como quando dizemos que o solo é energia potencial zero em um problema de energia potencial gravitacional) e a energia potencial de Q quando ela é separada de q por uma distância r assume a forma
\[\underbrace{U(r) = k\dfrac{qQ}{r}}_{zero \, reference \, at \, r = \infty}.\]
Essa fórmula é simétrica em relação a\(q\) e\(Q\), portanto, é melhor descrita como a energia potencial do sistema de duas cargas.
Uma\(+3.0-nC\) carga Q está inicialmente em repouso a uma distância de 10 cm\((r_1)\) de uma\(+5.0-nC\) carga q fixada na origem (Figura\(\PageIndex{6}\)). Naturalmente, a força de Coulomb acelera Q para longe de q, chegando a 15 cm\((r_2)\).
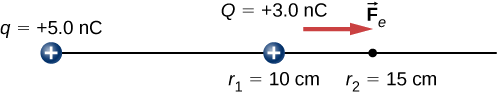
Qual é a mudança na energia potencial do sistema de duas cargas de\(r_1\) para\(r_2\)?
Estratégia
Calcule a energia potencial com a definição dada acima:
\(\Delta U_{12} = -\int_{r_1}^{r_2} \vec{F} \cdot d\vec{r}\). Como Q partiu do repouso, isso é o mesmo que a energia cinética.
Solução
Nós temos
\[\begin{align} \Delta U_{12} &= - \int_{r_1}^{r_2} \vec{F} \cdot d\vec{r} \nonumber \\[4pt] &= - \int_{r_1}^{r_2} \dfrac{kqQ}{r^2}dr \nonumber \\[4pt] &= - \left[ - \dfrac{kqQ}{r}\right]_{r_1}^{r_2} \nonumber \\[4pt] &=kqQ \left[ \dfrac{1}{r_2} - \dfrac{1}{r_1} \right] \nonumber \\[4pt] &= (8.99 \times 10^9 \, Nm^2/C^2)(5.0 \times 10^{-9} C)(3.0 \times 10^{-9} C) \left[ \dfrac{1}{0.15 \, m} - \dfrac{1}{0.10 \, m}\right] \nonumber \\[4pt] &= - 4.5 \times 10^{-7} \, J. \end{align} \]
Significância
A mudança na energia potencial é negativa, conforme esperado, e igual em magnitude à mudança na energia cinética neste sistema. Lembre-se do Example\(\PageIndex{1}\) que a mudança na energia cinética foi positiva.
Qual é a energia potencial de Q em relação à referência zero no infinito\(r_2\) no exemplo acima?
Solução
Tem energia cinética de\(4.5 \times 10^{-7} \, J\) no ponto\(r_2\) e energia potencial de\(9.0 \times 10^{-7} \, J\), o que significa que quando Q se aproxima do infinito, sua energia cinética totaliza três vezes a energia cinética em\(r_2\), já que toda a energia potencial é convertida em cinética.
Devido à lei de Coulomb, as forças devidas a várias cargas em uma carga de teste\(Q\) se sobrepõem; elas podem ser calculadas individualmente e depois adicionadas. Isso implica que as integrais de trabalho e, portanto, as energias potenciais resultantes exibem o mesmo comportamento. Para demonstrar isso, consideramos um exemplo de montagem de um sistema de quatro cargas.
Encontre a quantidade de trabalho que um agente externo deve realizar ao montar quatro cargas\(+2.0-\mu C\)\(+4.0-\mu C\) e\(+5.0-\mu C\) nos vértices de um quadrado de 1,0 cm de lado, iniciando cada carga do infinito (Figura\(\PageIndex{7}\)).\(+3.0-\mu C\)
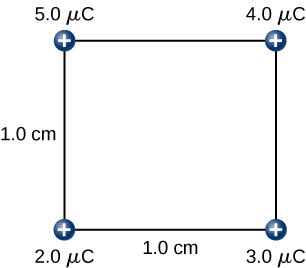
Estratégia
Nós trazemos as cargas uma de cada vez, fornecendo a elas locais iniciais no infinito e calculando o trabalho para trazê-las do infinito até a localização final. Fazemos isso em ordem crescente de cobrança.
Solução
Etapa 1. Primeiro, traga a\(+2.0-\mu C\) carga para a origem. Como ainda não há outras cargas a uma distância finita dessa carga, nenhum trabalho é feito para trazê-la do infinito,
\[W_1 = 0.\]
Etapa 2. Enquanto mantém a\(+2.0-\mu C\) carga fixa na origem, leve a\(+3.0-\mu C\) carga para\((x,y,z) = (1.0 \, cm, \, 0, \, 0)\) (Figura\(\PageIndex{8}\)). Agora, a força aplicada deve funcionar contra a força exercida pela\(+2.0-\mu C\) carga fixada na origem. O trabalho realizado é igual à mudança na energia potencial da\(+3.0-\mu C\) carga:
\[\begin{align} W_2 &= k\dfrac{q_1q_2}{r{12}} \nonumber \\[4pt] &= \left(9.0 \times 10^9 \frac{N \cdot m^2}{C^2}\right) \dfrac{(2.0 \times 10^{-6} C)(3.0 \times 10^{-6}C)}{1.0 \times 10^{-2} m} \nonumber \\[4pt] &= 5.4 \, J.\nonumber \end{align} \nonumber\]
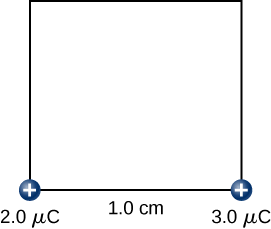
Etapa 3. Enquanto mantém as cargas\(+2.0-\mu C\) e\(+3.0-\mu C\) fixas em seus lugares, traga a\(+4.0-\mu C\) carga para\((x,y,z) = (1.0 \, cm, \, 1.0 \, cm, \, 0)\) (Figura)\(\PageIndex{9}\). O trabalho realizado nesta etapa é
\[\begin{align} W_3 &= k\dfrac{q_1q_3}{r_{13}} + k \dfrac{q_2q_3}{r_{23}} \nonumber \\[4pt] &= \left(9.0 \times 10^9 \frac{N \cdot m^2}{C^2}\right) \left[ \dfrac{(2.0 \times 10^{-6}C)(4.0 \times 10^{-6}C)}{\sqrt{2} \times 10^{-2}m} + \dfrac{(3.0 \times 10^{-6} C)(4.0 \times 10^{-6}C)}{1.0 \times 10^{-2} m}\right] \nonumber \\[4pt] &= 15.9 \, J. \nonumber \end{align} \nonumber\]
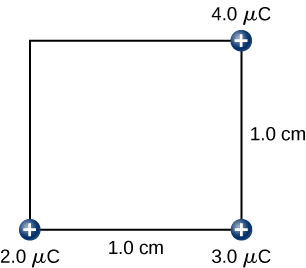
Etapa 4. Finalmente, mantendo as três primeiras cargas em seus lugares, leve a\(+5.0-\mu C\) carga para\((x,y,z) = (0, \, 1.0 \, cm, \, 0)\) (Figura\(\PageIndex{10}\)). O trabalho realizado aqui é
\[\begin{align} W_4 &= kq_4 \left[ \dfrac{q_1}{r_{14}} + \dfrac{q_2}{r_{24}} + \dfrac{q_3}{r_{34}}\right], \nonumber \\[4pt] &= \left(9.0 \times 10^9 \frac{N \cdot m^2}{C^2}\right)(5.0 \times 10^{-6}C) \left[ \dfrac{(2.0 \times 10^{-6}C)}{1.0 \times 10^{-2}m} + \dfrac{(3.0 \times 10^{-6} C)} {\sqrt{2} \times 10^{-2} m} + \dfrac{(4.0 \times 10^{-6}C)}{1.0 \times 10^{-2}m} \right] \nonumber \\[4pt] &= 36.5 \, J. \nonumber \end{align} \nonumber\]

Portanto, o trabalho total realizado pela força aplicada na montagem das quatro cargas é igual à soma do trabalho de levar cada carga do infinito à sua posição final:
\[\begin{align} W_T &= W_1 + W_2 + W_3 + W_4 \nonumber \\[4pt] &= 0 + 5.4 \, J + 15.9 \, J + 36.5 \, J \nonumber \\[4pt] &= 57.8 \, J. \nonumber \end{align} \nonumber\]
Significância
O trabalho em cada cobrança depende apenas de suas interações pareadas com as outras cobranças. Nenhuma interação mais complicada precisa ser considerada; o trabalho na terceira carga depende apenas de sua interação com a primeira e a segunda carga; a interação entre a primeira e a segunda carga não afeta a terceira.
A energia potencial elétrica das cargas de dois pontos é positiva ou negativa se as cargas forem do mesmo sinal? Sinais opostos? Como isso se relaciona com o trabalho necessário para aproximar as cargas do infinito?
Solução
positivo, negativo e essas quantidades são as mesmas do trabalho que você precisaria fazer para trazer as cargas do infinito
Observe que a energia potencial elétrica é positiva se as duas cargas forem do mesmo tipo, positivas ou negativas, e negativa se as duas cargas forem de tipos opostos. Isso faz sentido se você pensar na mudança na energia potencial\(\Delta U\) à medida que aproxima as duas cargas ou as afasta. Dependendo dos tipos relativos de cobranças, você pode ter que trabalhar no sistema ou o sistema funcionaria com você, ou seja, seu trabalho é positivo ou negativo. Se você precisar fazer um trabalho positivo no sistema (na verdade, aproximar as cargas), a energia do sistema deverá aumentar. Se você aproximar duas cargas positivas ou duas negativas, precisará fazer um trabalho positivo no sistema, o que aumenta sua energia potencial. Como a energia potencial é proporcional a 1/ r, a energia potencial aumenta quando r diminui entre duas cargas positivas ou duas negativas.
Por outro lado, se você aproximar uma carga positiva e uma negativa, precisará fazer um trabalho negativo no sistema (as cargas estão puxando você), o que significa que você retira energia do sistema. Isso reduz a energia potencial. Como a energia potencial é negativa no caso de um par de cargas positivas e negativas, o aumento em 1/ r torna a energia potencial mais negativa, o que é o mesmo que uma redução na energia potencial.
O resultado do Example\(\PageIndex{2}\) pode ser estendido a sistemas com qualquer número arbitrário de cobranças. Nesse caso, é mais conveniente escrever a fórmula como
\[W_{12 . . . N} = \dfrac{k}{2} \sum_i^N \sum_j^N \dfrac{q_iq_j}{r_{ij}} \, for \, i \neq j.\]
O fator 1/2 é responsável pela adição de cada par de cobranças duas vezes.


