4.6: O ciclo de Carnot

Objetivos de

Ao final desta seção, você poderá:

• Descreva o ciclo de Carnot com as funções de todos os quatro processos envolvidos
• Descreva o princípio de Carnot e suas implicações
• Demonstrar a equivalência do princípio de Carnot e da segunda lei da termodinâmica

No início da década de 1820, Sadi Carnot (1786 a 1832), engenheiro francês, ficou interessado em melhorar a eficiência de motores térmicos práticos. Em 1824, seus estudos o levaram a propor um ciclo de trabalho hipotético com a maior eficiência possível entre os mesmos dois reservatórios, conhecido agora como ciclo de Carnot. Um motor que opera nesse ciclo é chamado de motor Carnot. O ciclo de Carnot é de especial importância por vários motivos. Em um nível prático, esse ciclo representa um modelo reversível para a usina a vapor e o refrigerador ou bomba de calor. No entanto, também é muito importante teoricamente, pois desempenha um papel importante no desenvolvimento de outra declaração importante da segunda lei da termodinâmica. Finalmente, como apenas dois reservatórios estão envolvidos em sua operação, ele pode ser usado junto com a segunda lei da termodinâmica para definir uma escala absoluta de temperatura que seja verdadeiramente independente de qualquer substância usada para medição de temperatura.

Figura\(\PageIndex{1}\): Os quatro processos do ciclo de Carnot. A substância de trabalho é considerada um gás ideal cujo caminho termodinâmico MNOP é representado na Figura\(\PageIndex{2}\)

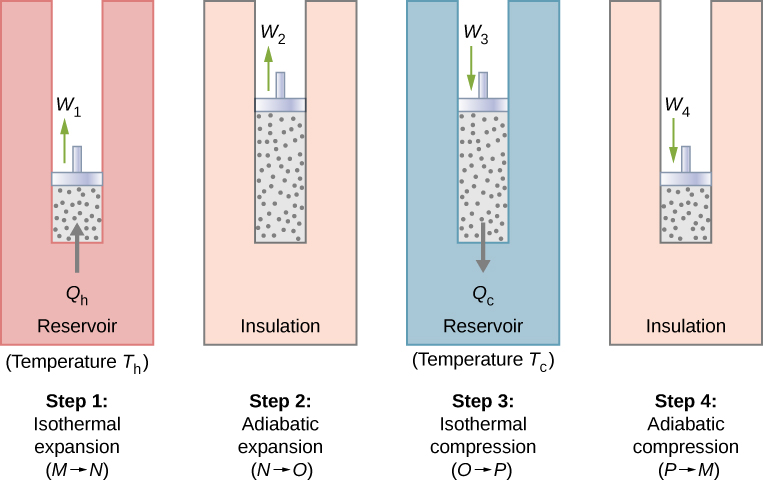
Com um gás ideal como substância de trabalho, as etapas do ciclo de Carnot, representadas pela Figura\(\PageIndex{1}\), são as seguintes.

1. Expansão isotérmica. O gás é colocado em contato térmico com um reservatório de calor a uma temperatura\(T_h\). O gás absorve o calor\(Q_h\) do reservatório de calor e pode se expandir isotermicamente, fazendo o trabalho\(W_1\). Como a energia interna\(E_{int}\) de um gás ideal é função somente da temperatura, a mudança da energia interna é zero, ou seja,\(\Delta E_{int} = 0\) durante essa expansão isotérmica. Com a primeira lei da termodinâmica,\(\Delta E_{int} = Q - W\), descobrimos que o calor absorvido pelo gás é\[Q_h = W_1 = nRT_h \ln \dfrac{V_N}{V_M}.\]
2. Expansão adiabática. O gás é isolado termicamente e pode se expandir ainda mais, fazendo o trabalho\(W_2\). Como essa expansão é adiabática, a temperatura do gás cai — neste caso, de\(T_h\) para\(T_c\). De\(pV^{\gamma} = constant\) e a equação de estado para um gás ideal\(pV = nRT\), temos\[TV^{\gamma - 1} = constant,\] para que\[T_hV_N^{\gamma - 1} = T_cV_O^{\gamma - 1}.\]
3. Compressão isotérmica. O gás é colocado em contato térmico com um reservatório frio à temperatura\(T_c\) e comprimido isotermicamente. Durante esse processo, o trabalho\(W_3\) é feito no gás e ele\(Q_c\) libera calor para o reservatório frio. O raciocínio usado na etapa 1 agora\[Q_c = nRT_c \ln \dfrac{V_O}{V_p},\] mostra onde\(Q_c\) está o calor despejado no reservatório frio pelo gás.
4. Compressão adiabática. O gás é isolado termicamente e retornado ao seu estado inicial por compressão. Nesse processo, o trabalho\(W_4\) é feito no gás. Como a compressão é adiabática, a temperatura do gás aumenta — de\(T_c\) para\(T_h\) neste caso específico. O raciocínio da etapa 2 agora fornece\[T_cV_p^{\gamma - 1} = T_hV_M^{\gamma - 1}.\] O trabalho total realizado pelo gás no ciclo de Carnot é dado por\[W = W_1 + W_2 - W_3 - W_4.\]

Figura\(\PageIndex{2}\): O trabalho total realizado pelo gás no ciclo de Carnot é mostrado e dado pela área delimitada pelo circuito MNOPM.

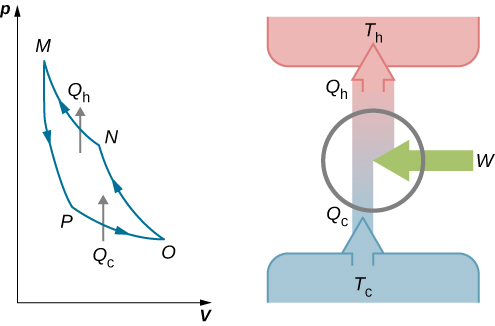
Este trabalho é igual à área delimitada pelo circuito mostrado no diagrama pV da Figura\(\PageIndex{2}\). Como os estados inicial e final do sistema são os mesmos, a mudança da energia interna do gás no ciclo deve ser zero, ou seja,\(\Delta E_{int} = 0\). A primeira lei da termodinâmica então dá\[W = Q - \Delta E_{int} = (Q_h - Q_c) - 0,\]\[W = Q_h - Q_c\] e.

Para encontrar a eficiência desse motor, primeiro dividimos\(Q_c\) por\(Q_h\):

\[\dfrac{Q_c}{Q_h} = \dfrac{T_c}{T_h} \dfrac{\ln V_O/V_P}{\ln V_N?V_M}.\]

Quando a constante adiabática da etapa 2 é dividida pela da etapa 4, encontramos

\[\dfrac{V_O}{V_P} = \dfrac{V_N}{V_M}.\]

Substituindo isso na equação por\(Q_c/Q_h\), obtemos

\[\dfrac{Q_c}{Q_h} = \dfrac{T_c}{T_h}.\]

Finalmente, com a Equação 4.3.6, descobrimos que a eficiência desse motor Carnot a gás ideal é dada por

\[e = 1 - \dfrac{T_c}{T_h}.\]

Um motor não precisa necessariamente seguir um ciclo de motor Carnot. Todos os motores, no entanto, têm o mesmo efeito líquido, ou seja, a absorção de calor de um reservatório quente, a produção de trabalho e o descarte de calor em um reservatório frio. Isso nos leva a perguntar: todos os ciclos reversíveis operando entre os mesmos dois reservatórios têm a mesma eficiência? A resposta a essa pergunta vem da segunda lei da termodinâmica discutida anteriormente: Todos os ciclos reversíveis do motor produzem exatamente a mesma eficiência. Além disso, como você pode esperar, todos os motores reais operando entre dois reservatórios são menos eficientes do que os motores reversíveis operando entre os mesmos dois reservatórios. Isso também é uma consequência da segunda lei da termodinâmica mostrada anteriormente.

O ciclo de um refrigerador Carnot a gás ideal é representado pelo diagrama pV da Figura\(\PageIndex{3}\). É um motor Carnot operando em sentido inverso. O refrigerador extrai calor\(Q_c\) de um reservatório de temperatura fria\(T_c\) quando o gás ideal se expande isotermicamente. O gás é então comprimido adiabaticamente até que sua temperatura atinja\(T_h\), após o que uma compressão isotérmica do gás faz com que o calor\(Q_h\) seja descartado em um reservatório de alta temperatura em\(T_h\). Finalmente, o ciclo é completado por uma expansão adiabática do gás, fazendo com que sua temperatura caia para\(T_c\).

Figura\(\PageIndex{3}\). O trabalho realizado com o gás em um ciclo do refrigerador Carnot é mostrado e dado pela área delimitada pelo circuito MPONM.

O trabalho realizado no gás ideal é igual à área delimitada pelo caminho do diagrama pV. A partir da primeira lei, esse trabalho é dado por

\[W = Q_h - Q_c.\]

Uma análise, assim como a análise feita para o motor Carnot, fornece

\[\dfrac{Q_c}{T_c} = \dfrac{Q_h}{T_h}.\]

Quando combinado com a Equação 4.4.1, isso produz

\[K_R = \dfrac{T_c}{T_h - T_c}\]

para o coeficiente de desempenho do refrigerador Carnot a gás ideal. Da mesma forma, podemos calcular o coeficiente de desempenho de uma bomba de calor Carnot como

\[K_P = \dfrac{Q_h}{Q_h - Q_c} = \dfrac{T_h}{T_h - T_c}.\]

Acabamos de encontrar equações que representam a eficiência de um motor Carnot e o coeficiente de desempenho de um refrigerador Carnot ou de uma bomba de calor Carnot, assumindo um gás ideal para a substância de trabalho em ambos os dispositivos. No entanto, essas equações são mais gerais do que suas derivações implicam. Em breve mostraremos que ambos são válidos, independentemente da substância ativa.

Carnot resumiu seu estudo sobre o motor de Carnot e o ciclo de Carnot no que hoje é conhecido como princípio de Carnot:

Princípio de Carnot

Nenhum motor trabalhando entre dois reservatórios em temperaturas constantes pode ter uma eficiência maior do que um motor reversível.

Esse princípio pode ser visto como outra afirmação da segunda lei da termodinâmica e pode ser mostrado como equivalente à declaração de Kelvin e à declaração de Clausius.

Exemplo\(\PageIndex{1}\): The Carnot Engine

Um motor Carnot tem uma eficiência de 0,60 e a temperatura de seu reservatório frio é de 300 K. (a) Qual é a temperatura do reservatório quente? (b) Se o motor fizer 300 J de trabalho por ciclo, quanto calor é removido do reservatório de alta temperatura por ciclo? (c) Quanto calor é expelido para o reservatório de baixa temperatura por ciclo?

Estratégia

A partir da dependência da temperatura da eficiência térmica do motor Carnot, podemos encontrar a temperatura do reservatório quente. Então, a partir da definição da eficiência, podemos encontrar o calor removido quando o trabalho realizado pelo motor é fornecido. Finalmente, a conservação de energia levará à quantidade de calor que deve ser despejada no reservatório de frio.

Solução

1. De\(e = 1 - T_c/T_h\) nós temos\[0.60 = 1 - \dfrac{300 \, K}{T_h},\] para que a temperatura do reservatório quente seja\[T_h = \dfrac{300 \, K}{1 - 0.60} = 750 \, K.\]
2. Por definição, a eficiência do motor é\(e = W/Q\), de modo que o calor removido do reservatório de alta temperatura por ciclo é\[Q_h = \dfrac{W}{e} = \dfrac{300 \, J}{0.60} = 500 \, J.\]
3. Desde a primeira lei, o calor exaurido para o reservatório de baixa temperatura por ciclo pelo motor é\[Q_c = Q_h - W = 500 \, J - 300 \, J = 200 \, J.\]

Significância

Um motor Carnot tem a máxima eficiência possível de converter calor em trabalho entre dois reservatórios, mas isso não significa necessariamente que seja\(100\%\) eficiente. À medida que a diferença nas temperaturas do reservatório quente e frio aumenta, a eficiência de um motor Carnot aumenta.

Exemplo\(\PageIndex{2}\): A Carnot Heat Pump

Imagine que uma bomba de calor Carnot opera entre uma temperatura externa de\(0^oC\) e uma temperatura interna de\(20.0^oC\). Qual é o trabalho necessário se o calor fornecido ao interior da casa for de 30,0 kJ?

Estratégia

Como a bomba de calor é considerada uma bomba de Carnot, seu coeficiente de desempenho é dado por\(K_P = Q_h/W = T_h/(T_h - T_c)\). Assim, podemos encontrar o trabalho W a partir do calor fornecido\(Q_h\).

Solução

O trabalho necessário é obtido em

\[W = Q_h/K_P = Q_h(T_h - T_c)/T_h = 30 \, kJ \times (293 \, K - 273 \, K)/293 \, K = 2 \, kJ. \nonumber\]

Significância

Observamos que esse trabalho depende não apenas do calor fornecido à casa, mas também das temperaturas externas e internas. A dependência da temperatura externa torna impraticável o uso em áreas onde a temperatura externa é muito mais fria do que a temperatura ambiente.

Em termos de custos de energia, a bomba de calor é um meio muito econômico para aquecer edifícios (Figura\(\PageIndex{4}\)). Compare esse método com a transformação de energia elétrica diretamente em calor com elementos de aquecimento resistivos. Nesse caso, uma unidade de energia elétrica fornece no máximo apenas uma unidade de calor. Infelizmente, as bombas de calor têm problemas que limitam sua utilidade. Eles são muito caros de comprar em comparação com elementos de aquecimento resistivos e, como mostra o coeficiente de desempenho de uma bomba de calor Carnot, eles se tornam menos eficazes à medida que a temperatura externa diminui. Na verdade, abaixo de aproximadamente\(-10^oC\), o calor que eles fornecem é menor do que a energia usada para operá-los.

Figura\(\PageIndex{4}\). Uma fotografia de uma bomba de calor (caixa grande) localizada fora de uma casa. Essa bomba de calor está localizada em uma área de clima quente, como o sul dos Estados Unidos, pois seria muito ineficiente localizada na metade norte dos Estados Unidos. (crédito: modificação da obra de Peter Stevens).

Exercício\(\PageIndex{1}\)

Um motor Carnot opera entre reservatórios em\(400^oC\)\(30^oC\) e.

1. Qual é a eficiência do motor?
2. Se o motor faz 5,0 J de trabalho por ciclo, quanto calor por ciclo ele absorve do reservatório de alta temperatura?
3. Quanto calor por ciclo ele libera para o reservatório de temperatura fria?
4. Quais temperaturas no reservatório frio proporcionariam a eficiência mínima e máxima?

Responda a

\(e = 1 - T_c/T_h = 0.55\)

Resposta b

\(Q_h = eW = 9.1 \, J\)

Resposta c

\(Q_c = Q_h - W = 4.1 \, J\)

Resposta d

\(-273^oC\)e\(400^oC\)

Exercício\(\PageIndex{2}\)

Um refrigerador Carnot opera entre dois reservatórios de calor cujas temperaturas são\(0^oC\)\(25^oC\) e.

1. Qual é o coeficiente de desempenho do refrigerador?
2. Se 200 J de trabalho forem feitos na substância de trabalho por ciclo, quanto calor por ciclo é extraído do reservatório frio?
3. Quanto calor por ciclo é descartado no reservatório quente?

Responda a

\(K_R = T_c/(T_h - T_c) = 10.9\)

Resposta b

\(Q_c = K_RW = 2.18 \, kJ\)

Resposta c

\(Q_h = Q_c + W = 2.38 \, kJ\)