4.5: Declarações da Segunda Lei da Termodinâmica
- Page ID
- 184596
Ao final desta seção, você poderá:
- Compare as declarações da segunda lei da termodinâmica de acordo com as formulações de Kelvin e Clausius
- Interprete a segunda da termodinâmica via irreversibilidade
No início deste capítulo, apresentamos a declaração de Clausius da segunda lei da termodinâmica, que se baseia na irreversibilidade do fluxo de calor espontâneo. Como observamos então, a segunda lei da termodinâmica pode ser declarada de várias maneiras diferentes, e pode-se mostrar que todas elas implicam as outras. Em termos de motores térmicos, a segunda lei da termodinâmica pode ser declarada da seguinte forma:
É impossível converter o calor de uma única fonte em trabalho sem nenhum outro efeito.
Isso é conhecido como a declaração Kelvin da segunda lei da termodinâmica. Esta declaração descreve um “motor perfeito” inatingível, conforme representado esquematicamente na Figura\(\PageIndex{1a}\). Observe que “sem nenhum outro efeito” é uma restrição muito forte. Por exemplo, um motor pode absorver calor e transformar tudo em trabalho, mas não se completar um ciclo. Sem completar um ciclo, a substância no motor não está em seu estado original e, portanto, ocorreu um “outro efeito”. Outro exemplo é uma câmara de gás que pode absorver o calor de um reservatório de calor e trabalhar isotermicamente contra um pistão à medida que ele se expande. No entanto, se o gás voltasse ao seu estado inicial (ou seja, feito para completar um ciclo), ele teria que ser comprimido e o calor teria que ser extraído dele.
A declaração de Kelvin é uma manifestação de um conhecido problema de engenharia. Apesar do avanço da tecnologia, não conseguimos construir um motor térmico que seja\(100\%\) eficiente. A primeira lei não exclui a possibilidade de construir um motor perfeito, mas a segunda lei o proíbe.
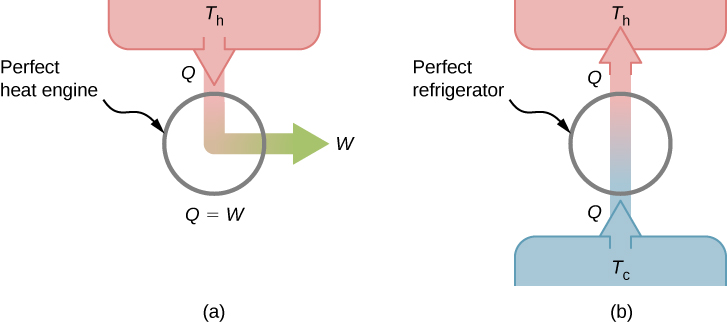
Podemos mostrar que a declaração de Kelvin é equivalente à declaração de Clausius se considerarmos os dois objetos na declaração de Clausius como um reservatório frio e um reservatório quente. Assim, a declaração de Clausius passa a ser: É impossível construir um refrigerador que transfira calor de um reservatório frio para um reservatório quente sem o auxílio de uma fonte externa. A declaração de Clausius está relacionada à observação diária de que o calor nunca flui espontaneamente de um objeto frio para um objeto quente. A transferência de calor na direção do aumento da temperatura sempre requer alguma entrada de energia. Uma “geladeira perfeita”, mostrada na Figura\(\PageIndex{1b}\), que funciona sem essa ajuda externa, é impossível de construir.
Para provar a equivalência das afirmações de Kelvin e Clausius, mostramos que se uma afirmação é falsa, necessariamente se segue que a outra afirmação também é falsa. Vamos primeiro supor que a afirmação de Clausius seja falsa, de modo que o refrigerador perfeito da Figura\(\PageIndex{1b}\) existe. O refrigerador remove o calor Q de um reservatório frio em uma temperatura\(T_c\) e transfere tudo para um reservatório quente em uma temperatura\(T_h\). Agora, considere um motor térmico real trabalhando na mesma faixa de temperatura. Ele extrai calor\(Q + \Delta Q\) do reservatório quente, funciona W e descarta o calor Q no reservatório frio. Da primeira lei, essas quantidades são relacionadas por
\[W = (Q + \Delta Q) - Q = \Delta Q.\]
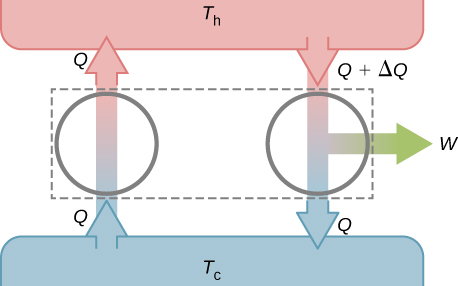
Suponha que esses dois dispositivos sejam combinados conforme mostrado na Figura\(\PageIndex{2}\). O calor líquido removido do reservatório quente é\(\Delta Q\), nenhuma transferência líquida de calor ocorre para ou do reservatório frio, e o trabalho W é feito em algum corpo externo. Pois\(W = \Delta Q\), a combinação de um refrigerador perfeito e um verdadeiro motor térmico é, em si, um motor térmico perfeito, contradizendo assim a declaração de Kelvin. Portanto, se a declaração de Clausius for falsa, a declaração de Kelvin também deve ser falsa.
Usando a segunda lei da termodinâmica, agora provamos duas propriedades importantes dos motores térmicos operando entre dois reservatórios de calor. A primeira propriedade é que qualquer motor reversível operando entre dois reservatórios tem uma eficiência maior do que qualquer motor irreversível operando entre os mesmos dois reservatórios.
A segunda propriedade a ser demonstrada é que todos os motores reversíveis operando entre os mesmos dois reservatórios têm a mesma eficiência. Para mostrar isso, começamos com os dois motores D e E da Figura\(\PageIndex{3a}\), que operam entre dois reservatórios de calor comuns em temperaturas\(T_h\)\(T_c\) e. Primeiro, assumimos que D é um motor reversível e que E é um motor hipotético irreversível que tem uma eficiência maior do que D. Se ambos os motores realizam a mesma quantidade de trabalho\(W\) por ciclo, isso resulta\(e=\frac{W}{Q_h}=1-\frac{Q_C}{Q_h}\) disso\(Q_h > Q'_h\). Em seguida, decorre da primeira lei que\(Q_c > Q'_c\).
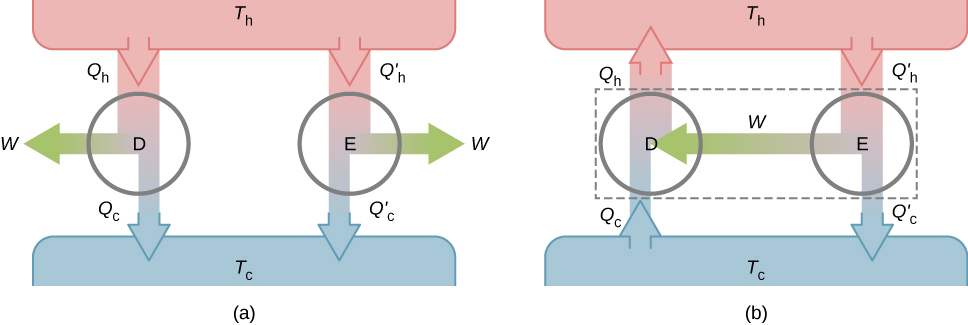
Suponha que o ciclo de D seja invertido para operar como um refrigerador e os dois motores estejam acoplados de forma que a potência de trabalho de E seja usada para acionar D, conforme mostrado na Figura\(\PageIndex{3b}\). Como\(Q_h > Q'_h\) e\(Q_c > Q'_c\), o resultado líquido de cada ciclo é equivalente a uma transferência espontânea de calor do reservatório frio para o reservatório quente, um processo que a segunda lei não permite. A suposição original deve, portanto, estar errada, e é impossível construir um motor irreversível de tal forma que E seja mais eficiente que o motor reversível D.
Agora é muito fácil demonstrar que as eficiências de todos os motores reversíveis operando entre os mesmos reservatórios são iguais. Suponha que D e E sejam ambos motores reversíveis. Se eles estiverem acoplados conforme mostrado na Figura\(\PageIndex{3b}\), a eficiência de E não pode ser maior que a eficiência de D, ou a segunda lei seria violada. Se ambos os motores forem então invertidos, o mesmo raciocínio implica que a eficiência de D não pode ser maior que a eficiência de E. A combinação desses resultados leva à conclusão de que todos os motores reversíveis que trabalham entre os mesmos dois reservatórios têm a mesma eficiência.
Qual é a eficiência de um motor térmico perfeito? Qual é o coeficiente de desempenho de um refrigerador perfeito?
Solução
Um motor térmico perfeito teria\(Q_c = 0\), o que levaria\(e = 1 - Q_c/Q_h = 1\) a. Um refrigerador perfeito precisaria de zero trabalho, ou seja\(W = 0\), o que leva\(K_R = Q_c/W \rightarrow \infty\) a.
Mostre isso\(Q_h - Q'_h = Q_c - Q'_c\) para o motor hipotético da Figura\(\PageIndex{1b}\).
Solução
Do motor à direita, temos\(W = Q'_h - Q'_c\). Da geladeira à direita, temos\(Q_h = Q_c + W\). Assim\(W = Q'_h - Q'_c = Q_h - Q_c\).


