4.7: Entropia
- Page ID
- 184606
Ao final desta seção, você poderá:
- Descreva o significado da entropia
- Calcule a mudança de entropia para alguns processos simples
A segunda lei da termodinâmica é melhor expressa em termos de uma mudança na variável termodinâmica conhecida como entropia, que é representada pelo símbolo S. A entropia, como a energia interna, é uma função estatal. Isso significa que quando um sistema faz uma transição de um estado para outro, a mudança na entropia\(\Delta S\) é independente do caminho e depende apenas das variáveis termodinâmicas dos dois estados.
Primeiro, consideramos um sistema passando\(\Delta S\) por um processo reversível a uma temperatura constante. Nesse caso, a mudança na entropia do sistema é dada por
\[\Delta S = \dfrac{Q}{T}, \label{eq1}\]
onde\(Q\) está o calor trocado pelo sistema mantido a uma temperatura T (em kelvin). Se o sistema absorver calor, ou seja, com\(Q > 0\), a entropia do sistema aumenta. Como exemplo, suponha que um gás seja mantido a uma temperatura constante de 300 K enquanto absorve 10 J de calor em um processo reversível. Então, da Equação\ ref {eq1}, a mudança de entropia do gás é
\[\Delta S = \dfrac{10 \, J}{300 \, K} = 0.033 \, J/K.\]
Da mesma forma, se o gás perder 5,0 J de calor; ou seja\(Q = -5.0 \, J\), à temperatura\(T = 200 \, K\), temos a mudança de entropia do sistema dada por
\[\Delta S = \dfrac{-5.0 \, J}{200 \, K} = -0.025 \, J/K.\]
O calor é adicionado lentamente a um pedaço de gelo de 50 g\(0^oC\) até que ele derreta completamente na água na mesma temperatura. Qual é a mudança de entropia do gelo?
Estratégia
Como o processo é lento, podemos aproximá-lo como um processo reversível. A temperatura é constante e, portanto, podemos usar a Equação\ ref {eq1} no cálculo.
Solução
O gelo é derretido pela adição de calor:\[Q = mL_f = 50 \, g \times 335 \, J/g = 16.8 \, kJ. \nonumber\]
Neste processo reversível, a temperatura da mistura gelada-água é fixada em\(0^oC\) ou 273 K. Agora, a partir de\(\Delta S = Q/T\), a mudança de entropia do gelo é
\[\Delta S = \dfrac{16.8 \, kJ}{273 \, K} = 61.5 \, J/K \nonumber\]
quando derrete em água em\(0^oC\).
Significância
Durante uma mudança de fase, a temperatura é constante, o que nos permite usar a Equação\ ref {eq1} para resolver esse problema. A mesma equação também poderia ser usada se mudássemos de uma fase líquida para uma fase gasosa, já que a temperatura também não muda durante esse processo.
A mudança na entropia de um sistema para uma transição arbitrária e reversível para a qual a temperatura não é necessariamente constante é definida pela modificação\(\Delta S = Q/T\). Imagine um sistema fazendo uma transição do estado A para B em etapas pequenas e discretas. As temperaturas associadas a esses estados são\(T_A\) e\(T_B\), respectivamente. Durante cada etapa da transição, o sistema troca calor de\(\Delta Q_i\) forma reversível a uma temperatura\(T_i\). Isso pode ser feito experimentalmente colocando o sistema em contato térmico com um grande número de reservatórios de calor de temperaturas variadas\(T_i\), conforme ilustrado na Figura\(\PageIndex{1}\). A mudança na entropia para cada etapa é\(\Delta S_i = Q_i/T_i\). A mudança líquida na entropia do sistema para a transição é
\[\Delta S = S_B - S_A = \sum_i \Delta S_i = \sum_i \dfrac{\Delta Q_i}{T_i}. \nonumber\]
Agora tomamos o limite à medida que\(\Delta Q_i \rightarrow 0\), e o número de etapas se aproxima do infinito. Então, substituindo a soma por uma integral, obtemos
\[\Delta S = S_B - S_A = \int_A^B \dfrac{dQ}{T}, \label{eq5} \]
onde a integral é obtida entre o estado inicial A e o estado final B. Essa equação é válida somente se a transição de A para B for reversível.
Como exemplo, vamos determinar a mudança de entropia líquida de um motor reversível enquanto ele passa por um único ciclo de Carnot. Nas etapas adiabáticas 2 e 4 do ciclo mostrado na Figura\(\PageIndex{1}\), nenhuma troca de calor ocorre, então\(\Delta S_2 = \Delta S_4 = \int dQ/T = 0\). Na etapa 1, o motor absorve calor a uma\(Q_h\) temperatura\(T_h\), então sua mudança de entropia é\(\Delta S_1 = Q_h/T_h\). Da mesma forma, na etapa 3,\(\Delta S_3 = -Q_c/T_c\). A mudança de entropia líquida do motor em um ciclo de operação é então
\[\Delta S_E = \Delta S_1 + \Delta S_2 + \Delta S_3 + \Delta S_4 = \dfrac{Q_h}{T_h} - \dfrac{Q_c}{T_c}.\]
No entanto, sabemos que para um motor Carnot,
\[\dfrac{Q_h}{T_h} = \dfrac{Q_c}{T_c},\]
então
\[\Delta S_E = 0.\]
Não há nenhuma mudança líquida na entropia do motor Carnot durante um ciclo completo. Embora esse resultado tenha sido obtido para um caso específico, sua validade pode ser mostrada como muito mais geral: não há mudança líquida na entropia de um sistema passando por qualquer processo cíclico reversível completo. Matematicamente, escrevemos essa declaração como
\[\oint dS = \oint \dfrac{dQ}{T} = 0 \label{eq10}\]
onde\(\oint\) representa a integral em um caminho reversível fechado.
Podemos usar a Equação\ ref {eq10} para mostrar que a mudança de entropia de um sistema passando por um processo reversível entre dois estados dados é independente do caminho. Um caminho arbitrário e fechado para um ciclo reversível que passa pelos estados A e B é mostrado na Figura\(\PageIndex{2}\). A partir da Equação\ ref {eq10}, sabemos que\(\oint dS = 0\) para esse caminho fechado. Podemos dividir essa integral em dois segmentos, um ao longo de I, que leva de A a B, o outro ao longo de II, que leva de B a A. Então
\[\left[\int_A^BdS\right]_I + \left[\int_B^A dS\right]_{II} = 0\]
Como o processo é reversível,
\[\left[\int_A^B dS\right] = \left[\int_A^B dS\right] \nonumber\]
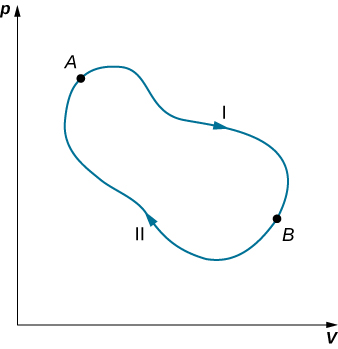
Portanto, a mudança de entropia ao ir de A para B é a mesma para os caminhos I e II. Como os caminhos I e II são caminhos arbitrários e reversíveis, a mudança de entropia em uma transição entre dois estados de equilíbrio é a mesma para todos os processos reversíveis que unem esses estados. A entropia, como a energia interna, é, portanto, uma função de estado.
O que acontece se o processo for irreversível? Quando o processo é irreversível, esperamos que a entropia de um sistema fechado, ou o sistema e seu ambiente (o universo), aumentem. Portanto, podemos reescrever essa expressão como
\[\Delta S \geq 0,\nonumber \]
onde\(S\) está a entropia total do sistema fechado ou do universo inteiro, e o sinal de igual é para um processo reversível. O fato é a declaração de entropia da segunda lei da termodinâmica:
A entropia de um sistema fechado e de todo o universo nunca diminui.
Podemos mostrar que essa afirmação é consistente com a declaração de Kelvin, a declaração de Clausius e o princípio de Carnot.
Determine a mudança de entropia de um objeto de massa m e calor específico c que é resfriado rapidamente (e irreversivelmente) a uma pressão constante de\(T_h\) para\(T_c\).
Estratégia
O processo é claramente declarado como um processo irreversível; portanto, não podemos simplesmente calcular a mudança de entropia do processo real. No entanto, como a entropia de um sistema é uma função do estado, podemos imaginar um processo reversível que começa no mesmo estado inicial e termina no estado final dado. Em seguida, a mudança de entropia do sistema é dada pela Equação\ ref {eq5},\(\Delta S = \int_A^B dQ/T\).
Solução
Para substituir esse resfriamento rápido por um processo que ocorre de forma reversível, imaginamos que o objeto quente seja colocado em contato térmico com reservatórios de calor sucessivamente mais frios, cujas temperaturas variam\(T_h\) de\(T_c\) a. Durante a transição substituta, o objeto perde quantidades infinitesimais de calor dQ, então temos
\[\Delta S = \int_{T_h}^{T_c} \dfrac{dQ}{T}. \nonumber\]
A partir da definição de capacidade térmica, uma troca infinitesimal dQ pelo objeto está relacionada à sua mudança de temperatura dT por
\[dQ = mcdT. \nonumber\]
Substituindo esse dQ na expressão,\(\Delta S\) obtemos a mudança de entropia do objeto à medida que ele é resfriado a uma pressão constante de\(T_h\) para\(T_c\):
\[\Delta S = \int_{T_h}^{T_c} \dfrac{mcdT}{T} = mcln\dfrac{T_c}{T_h}. \nonumber\]
Observe isso\(\Delta S < 0\) aqui porque\(T_c > T_h\). Em outras palavras, o objeto perdeu alguma entropia. Mas se contarmos o que for usado para remover o calor do objeto, ainda assim acabaríamos\(S_{universe} > 0\) porque o processo é irreversível.
Significância
Se a temperatura mudar durante o fluxo de calor, você deve mantê-la dentro da integral para resolver a mudança na entropia. Se, no entanto, a temperatura for constante, você pode simplesmente calcular a mudança de entropia como o fluxo de calor dividido pela temperatura.
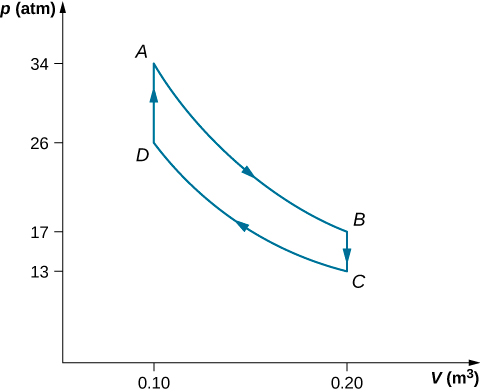
As etapas de um motor Stirling reversível são as seguintes. Para esse problema, usaremos 0,0010 mol de um gás monoatômico que começa a uma temperatura de\(133^oC\) e\(0.10 m^3\) cujo volume será chamado de ponto A. Em seguida, ele segue as seguintes etapas:
- Etapa AB: expansão isotérmica\(33^oC\) de\(0.20 \, m^3\) para\(0.10 \, m^3\)
- Etapa BC: resfriamento isocórico para\(33^oC\)
- CD da etapa: compressão isotérmica\(33^oC\) de\(0.20 \, m^3\) até\(0.10 \, m^3\)
- Etapa DA: aquecimento isocórico de volta para\(133^oC\) e\(0.10 \, m^3\)
(a) Desenhe o diagrama pV para o motor Stirling com as etiquetas adequadas.
(b) Preencha a tabela a seguir.
| Etapa | W (J) | Q (J) | \(\Delta S\)(J/K) |
|---|---|---|---|
| Etapa AB | \ (\ Delta S\) (J/K) "> | ||
| Etapa BC | \ (\ Delta S\) (J/K) "> | ||
| CD de etapas | \ (\ Delta S\) (J/K) "> | ||
| Etapa DA | \ (\ Delta S\) (J/K) "> | ||
| Ciclo completo | \ (\ Delta S\) (J/K) "> |
(c) Como a eficiência do motor Stirling se compara à do motor Carnot trabalhando nos mesmos dois reservatórios de calor?
Estratégia
Usando a lei do gás ideal, calcule a pressão em cada ponto para que eles possam ser rotulados no diagrama pV. O trabalho isotérmico é calculado usando\(W = nRT \, ln\left(\frac{V_2}{V_1}\right)\), e um processo isocórico não tem trabalho realizado. O fluxo de calor é calculado a partir da primeira lei da termodinâmica,\(Q = \Delta E_{int} - W\) onde\(\Delta E_{int} = \frac{3}{2}nR\Delta T\) para gases monoatômicos. As etapas isotérmicas têm uma mudança na entropia de Q/T, enquanto as etapas isocóricas têm\(\Delta S = \frac{3}{2}n R \, ln \left(\frac{T_2}{T_1} \right)\). A eficiência de um motor térmico é calculada usando\(e_{Stir} = W/Q_h\).
Solução
- O gráfico é mostrado abaixo.
- A tabela completa é mostrada abaixo.
Etapa W (J) Q (J) \(\Delta S\)(J/K) Etapa AB Isotherm 2.3 2.3 \ (\ Delta S\) (J/K) ">0,0057 Etapa BC Isocórica 0 —1,2 \ (\ Delta S\) (J/K) ">0,0035 Etapa CD Isotherm —1,8 —1,8 \ (\ Delta S\) (J/K) ">—0,0059 Etapa DA: Isocórica 0 1.2 \ (\ Delta S\) (J/K) ">—0,0035 Ciclo completo 0,5 0,5 \ (\ Delta S\) (J/K) ">~ 0 - A eficiência do motor térmico Stirling é\[e_{Stir} = W/Q_h = (Q_{AB} + Q_{CD})/(Q_{AB} + Q{DA}) = 0.5/4.5 = 0.11. \nonumber\]
If this were a Carnot engine operating between the same heat reservoirs, its efficiency would be
\[e_{Car} = 1 - \left(\dfrac{T_c}{T_h} \right) = 0.25 \nonumber\]
Therefore, the Carnot engine would have a greater efficiency than the Stirling engine.
Significance
In the early days of steam engines, accidents would occur due to the high pressure of the steam in the boiler. Robert Stirling developed an engine in 1816 that did not use steam and therefore was safer. The Stirling engine was commonly used in the nineteenth century, but developments in steam and internal combustion engines have made it difficult to broaden the use of the Stirling engine.
The Stirling engine uses compressed air as the working substance, which passes back and forth between two chambers with a porous plug, called the regenerator, which is made of material that does not conduct heat as well. In two of the steps, pistons in the two chambers move in phase.


