10.4: Decaimento radioativo
- Page ID
- 183125
Ao final desta seção, você poderá:
- Descreva a decomposição de uma substância radioativa em termos de sua constante de decaimento e meia-vida
- Use a lei de decaimento radioativo para estimar a idade de uma substância
- Explique os processos naturais que permitem a datação de tecidos vivos usando 14 C
Em 1896, Antoine Becquerel descobriu que uma rocha rica em urânio emite raios invisíveis que podem escurecer uma placa fotográfica em um recipiente fechado. Os cientistas oferecem três argumentos para a origem nuclear desses raios. Primeiro, os efeitos da radiação não variam com o estado químico; ou seja, se o material emissor está na forma de um elemento ou composto. Em segundo lugar, a radiação não varia com as mudanças de temperatura ou pressão — ambos fatores que, em grau suficiente, podem afetar os elétrons em um átomo. Em terceiro lugar, a energia muito grande dos raios invisíveis (até centenas de eV) não é consistente com as transições atômicas de elétrons (apenas alguns eV). Hoje, essa radiação é explicada pela conversão de massa em energia nas profundezas do núcleo de um átomo. A emissão espontânea de radiação dos núcleos é chamada de radioatividade nuclear (Figura\(\PageIndex{1}\)).

Lei de decaimento radioativo
Quando um núcleo individual se transforma em outro com a emissão de radiação, diz-se que o núcleo se decompõe. O decaimento radioativo ocorre para todos os núcleos com\(Z > 82\), e também para alguns isótopos instáveis com\(Z < 83\). A taxa de decaimento é proporcional ao número de núcleos N originais (não decaídos) em uma substância. O número de núcleos perdidos para decair,\(-dN\) no intervalo de tempo dt, é escrito
\[-\dfrac{dN}{dt} = \lambda N \label{eq2} \]
onde\(\lambda\) é chamada de constante de decaimento. (O sinal de menos indica que o número de núcleos originais diminui com o tempo.) Em outras palavras, quanto mais núcleos disponíveis para decair, mais eles decaem (com o tempo dt). A equação\ ref {eq2} pode ser reescrita como
\[\dfrac{dN}{N} = -\lambda dt. \nonumber \]
Integrando os dois lados da equação e definindo\(N_0\) como sendo o número de núcleos em\(t = 0\), obtemos
\[\int_{N_0}^N \dfrac{dN'}{N} = - \int_0^t \lambda dt'. \nonumber \]
Isso nos dá
\[\ln\dfrac{N}{N_0} = -\lambda t. \label{eq4} \]
Tomando os lados esquerdo e direito da Equação\ ref {eq4} como uma potência de\(e\), temos a lei de decaimento radioativo.
O número total\(N\) de núcleos radioativos restantes após o tempo\(t\) é
\[N = N_0e^{-\lambda t} \label{decay law} \]
onde\(\lambda\) está a constante de decaimento para o núcleo em particular.
O número total de núcleos cai muito rapidamente no início e depois mais lentamente (Figura\(\PageIndex{2}\)).
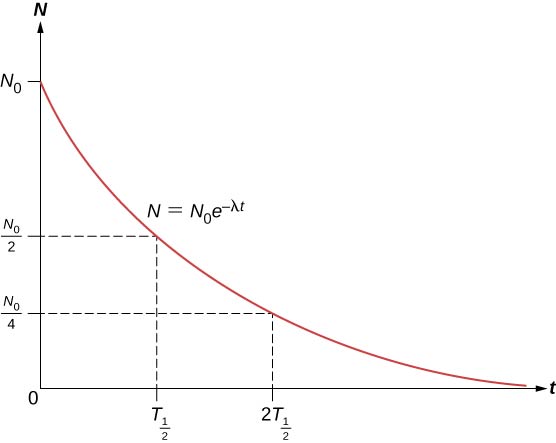
A meia-vida\((T_{1/2})\) de uma substância radioativa é definida como o tempo de decomposição da metade dos núcleos originais (ou o tempo em que metade dos núcleos originais permanecem). As meias-vidas dos isótopos instáveis são mostradas no gráfico dos nuclídeos. O número de núcleos radioativos restantes após um número inteiro (n) de meias-vidas é, portanto,
\[N = \dfrac{N_0}{2^n} \label{eq5} \]
Se a constante de decaimento\((\lambda)\) for grande, a meia-vida é pequena e vice-versa. Para determinar a relação entre essas quantidades, observe que quando\(t = T_{1/2}\), então\(N = N_0/2\).
Assim, a Equação\ ref {eq5} pode ser reescrita como
\[\dfrac{N_0}{2} = N_0e^{-\lambda T_{1/2}}. \nonumber \]
Dividindo os dois lados\(N_0\) e obtendo os resultados do logaritmo natural
\[\ln \dfrac{1}{2} = \ln \, e^{-\lambda T_{1/2}} \nonumber \]
que se reduz a
\[\lambda = \dfrac{0.693}{T_{1/2}}. \nonumber \]
Assim, se soubermos a meia-vida T 1/2 de uma substância radioativa, podemos encontrar sua constante de decaimento. A vida útil\(\overline{T}\) de uma substância radioativa é definida como a quantidade média de tempo que um núcleo existe antes de se decompor. O tempo de vida de uma substância é apenas o recíproco da constante de decaimento, escrito como
\[\overline{T} = \dfrac{1}{\lambda}. \nonumber \]
A atividade A é definida como a magnitude da taxa de decaimento, ou
\[A = -\dfrac{dN}{dt} = \lambda N = \lambda N_0 e^{-\lambda t}. \nonumber \]
A mudança infinitesimal dN no intervalo de tempo dt é negativa porque o número de partículas parentais (não decaídas) está diminuindo, então a atividade (A) é positiva. Definindo a atividade inicial como\(A_0 = \lambda N_0\), temos
\[A = A_0 e^{-\lambda t}. \label{eq8} \]
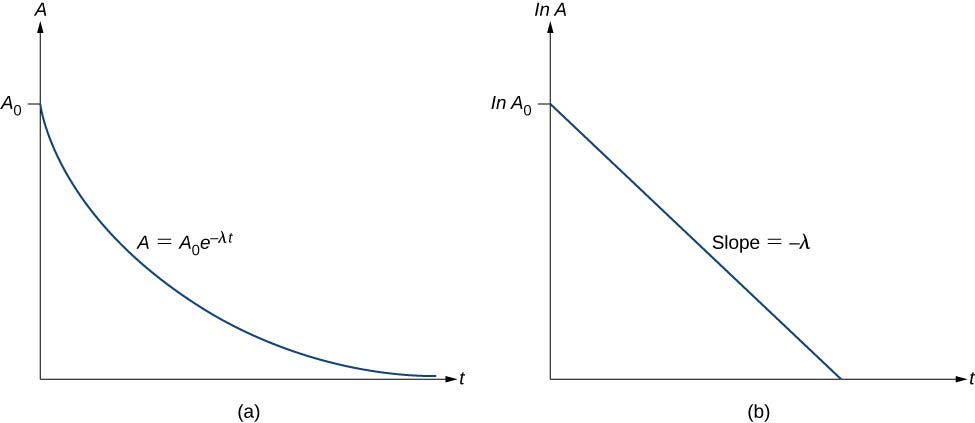
Assim, a atividade A de uma substância radioativa diminui exponencialmente com o tempo (Figura\(\PageIndex{3}\)).
A meia-vida do estrôncio-90,\(\ce{_{38}^{90}Sr}\), é de 28,8 y. Encontre (a) sua constante de decaimento e (b) a atividade inicial de 1,00 g do material.
Estratégia
Podemos encontrar a constante de decaimento diretamente da Equação\ ref {eq8}. Para determinar a atividade, primeiro precisamos encontrar o número de núcleos presentes.
Solução
a. A constante de decaimento é considerada
\[\lambda = \dfrac{0.693}{T_{1/2}} = \left(\dfrac{0.693}{T_{1/2}}\right)\left(\dfrac{1 \, yr}{3.16 \times 10^7 \, s}\right) = 7.61 \times 10^{-10} \, s^{-1}. \nonumber \]
b. A massa atômica de\(_{38}^{90}Sr\) é 89,91 g. Usando o número\(N_A = 6.022 \times 10^{23}\) átomos/mol de Avogadro, encontramos o número inicial de núcleos em 1,00 g do material:
\[N_0 = \dfrac{1.00 \, g}{89.91 \, g} (N_A) = 6.70 \times 10^{21} \, nuclei. \nonumber \]
A partir disso, descobrimos que a atividade\(A_0\)\(t = 0\) de 1,00 g de estrôncio-90 é
\[A_0 = \lambda N_0 = (7.61 \times 10^{-10} s^{-1})(6.70 \times 10^{21} \, nuclei) = 5.10 \times 10^{12} \, decays/s. \nonumber \]
Expressando\(\lambda\) em termos da meia-vida da substância, obtemos
\[A = A_0 e^{-(0.693/T_{1/2})T_{1/2}} = A_0 e^{-0.693} = A_0/2. \label{eq11} \]
Portanto, a atividade é reduzida pela metade após uma meia-vida. Podemos determinar a constante de decaimento\(\lambda\) medindo a atividade em função do tempo. Tomando o logaritmo natural dos lados esquerdo e direito da Equação\ ref {eq11}, obtemos
\[\ln \, A = - \lambda t + \ln \, A_0. \nonumber \]
Essa equação segue a forma linear\(y = mx + b\). Se traçarmos\ ln A versus t, esperamos uma linha reta com inclinação\(-\lambda\) e intercepto y\(\ln \, A_0\) (Figura\(\PageIndex{3b}\)). A atividade A é expressa em unidades de becquerels (Bq), onde um\(1 \, Bq = 1 \, decay \, per \, second\). Essa quantidade também pode ser expressa em decaimentos por minuto ou decaimentos por ano. Uma das unidades de atividade mais comuns é a curie (Ci), definida como sendo a atividade de 1 g de\(^{226}Ra\). A relação entre o Bq e o Ci é
\[1 \, Ci = 3.70 \times 10^{10}Bq. \nonumber \]
Aproximadamente\(20\%\) do corpo humano em massa é carbono. Calcule a atividade devida a\(^{14}C\) 1,00 kg de carbono encontrado em um organismo vivo. Expresse a atividade em unidades de Bq e Ci.
Estratégia
A atividade de\(^{14}C\) é determinada usando a equação\(A_0 = \lambda N_0\), onde λ é a constante de decaimento e\(N_0\) é o número de núcleos radioativos. O número de\(^{14}C\) núcleos em uma amostra de 1,00 kg é determinado em duas etapas. Primeiro, determinamos o número de\(^{12}C\) núcleos usando o conceito de toupeira. Em segundo lugar, multiplicamos esse valor por\(1.3 \times 10^{-12}\) (a abundância conhecida de\(^{14}C\) em uma amostra de carbono de um organismo vivo) para determinar o número de\(^{14}C\) núcleos em um organismo vivo. A constante de decaimento é determinada a partir da meia-vida conhecida de\(^{14}C\) (disponível em [link]).
Solução
Um mol de carbono tem uma massa de 12,0 g, já que é quase puro\(^{12}C\). Assim, o número de núcleos de carbono em um quilograma é
\[N(^{12}C) = \dfrac{6.02 \times 10^{23} mol^{-1}}{12.0 \, g/mol} \times (1000 \, g) = 5.02 \times 10^{25}. \nonumber \]
O número de\(^{14}C\) núcleos em 1 kg de carbono é, portanto,
\[N(^{14}C) = (5.02 \times 10^{25})(1.3 \times 10^{_12}) = 6.52 \times 10^{13}. \nonumber \]
Agora podemos encontrar a atividade\(A\) usando a Equação\ ref {eq11}. Inserir valores conhecidos nos dá
\[A = \dfrac{0.693 (6.52 \times 10^{13})}{5730 \, y} = 7.89 \times 10^9 \, y^{-1} \nonumber \]
ou\(7.89 \times 10^9\) decai por ano. Para converter isso na unidade Bq, simplesmente convertemos anos em segundos. Assim,
\[A = (7.89 \times 10^9 \, y^{-1}) \dfrac{1.00 \, y}{3.16 \times 10^7 \, s} = 250 \, Bq, \nonumber \]
ou 250 decaimentos por segundo. Para expressar A em curies, usamos a definição de curie,
\[A = \dfrac{250 \, Bq}{3.7 \times 10^{10} \, Bq/Ci} = 6.76 \times 10^{-9} Ci. \nonumber \]
Assim,
\[A = 6.76 \, nCi. \nonumber \]
Significância
Aproximadamente\(20\%\) do corpo humano em peso é carbono. Centenas de\(^{14}C\) decaimentos ocorrem no corpo humano a cada segundo. O carbono-14 e outras substâncias radioativas que ocorrem naturalmente no corpo compõem a exposição de fundo de uma pessoa à radiação nuclear. Como veremos mais adiante neste capítulo, esse nível de atividade está bem abaixo das dosagens máximas recomendadas.
Datação radioativa
A datação radioativa é uma técnica que usa radioatividade natural para determinar a idade de um material, como uma rocha ou um artefato antigo. A abordagem básica é estimar o número original de núcleos em um material e o número atual de núcleos no material (após o decaimento) e, em seguida, usar o valor conhecido da constante de decaimento\(\lambda\) e a Equação\ ref {lei de decaimento} para calcular o tempo total da decadência,\(t\).
Um método importante de datação radioativa é a datação por carbono 14. Os núcleos de carbono-14 são produzidos quando a radiação solar de alta energia atinge\(^{14}N\) os núcleos na alta atmosfera e, posteriormente, decaem com uma meia-vida de 5730 anos. O carbono radioativo tem a mesma química do carbono estável, então ele se combina com a ecosfera e, eventualmente, se torna parte de todos os organismos vivos. O carbono-14 tem uma abundância de 1,3 partes por trilhão de carbono normal. Portanto, se você souber o número de núcleos de carbono em um objeto, multiplique esse número por\(1.3 \times 10^{-12}\) para encontrar o número de\(^{14}C\) núcleos nesse objeto. Quando um organismo morre, a troca de carbono com o meio ambiente cessa e não\(^{14}C\) é reabastecido à medida que se decompõe.
Ao comparar a abundância de\(^{14}C\) em um artefato, como embalagens de múmias, com a abundância normal em tecidos vivos, é possível determinar a idade da múmia (ou o tempo desde a morte da pessoa). A datação por carbono-14 pode ser usada para tecidos biológicos de até 50.000 anos, mas geralmente é mais precisa para amostras mais jovens, já que a abundância de\(^{14}C\) núcleos nelas é maior. Materiais biológicos muito antigos não contêm\(^{14}C\) absolutamente nada. A validade da datação por carbono pode ser verificada por outros meios, como pelo conhecimento histórico ou pela contagem de anéis de árvores.
Em uma antiga caverna funerária, sua equipe de arqueólogos descobre móveis antigos de madeira. Somente\(80\%\) o original\(^{14}C\) permanece na madeira. Quantos anos tem a mobília?
Estratégia
A declaração do problema implica que\(N/N_0 = 0.80\). Portanto, reorganizamos a Equação\ ref {lei de decaimento} para encontrar o produto,\(\lambda t\). Sabemos que a meia-vida de\(^{14}C\) é de 5730 anos, então também sabemos a constante de decaimento e, portanto, o tempo total de decaimento\(t\).
Solução
Nós reorganizamos a Equação\ ref {lei de decaimento}\(N/N_0\) para dar
\[\dfrac{N}{N_0} = e^{-\lambda t}. \nonumber \]
Assim
\[0.80 = e^{-\lambda t}. \nonumber \]
Tomando o logaritmo natural de ambos os lados, obtém-se
\[\ln \, 0.80 = - \lambda t,\nonumber \]
para que
\[-0.223 = -\lambda t. \nonumber \]
Reorganizar a equação para isolar nos\(t\) dá
\[t = \dfrac{0.223}{\left(\dfrac{0.693}{5730 \, y}\right)} = 1844 \, y. \nonumber \]
Significância
A mobília tem quase 2000 anos — uma descoberta impressionante. A incerteza típica sobre a datação por carbono 14 é de cerca de\(5\%\), então a mobília tem entre 1750 e 1950 anos. Esse intervalo de datas deve ser confirmado por outras evidências, como registros históricos.
Um nuclídeo radioativo tem uma alta taxa de decaimento. O que isso significa para sua meia-vida e atividade?
- Resposta
-
A meia-vida está inversamente relacionada à taxa de decaimento, então a meia-vida é curta. A atividade depende do número de partículas em decomposição e da taxa de decaimento, então a atividade pode ser grande ou pequena.
Visite o Radioactive Dating Game para aprender sobre os tipos de datação radiométrica e tente datar alguns objetos antigos.


