9.3: Espectros moleculares
- Page ID
- 182809
Ao final desta seção, você poderá:
- Use os conceitos de energia vibracional e rotacional para descrever transições de energia em uma molécula diatômica
- Explicar as principais características de um espectro de energia vibracional-rotacional de uma molécula diatômica
- Estime as energias permitidas de uma molécula rotativa
- Determine a distância de separação de equilíbrio entre átomos em uma molécula diatômica a partir do espectro de absorção vibracional-rotacional
Os níveis de energia molecular são mais complicados do que os níveis de energia atômica porque as moléculas também podem vibrar e girar. As energias associadas a esses movimentos estão em diferentes faixas e, portanto, podem ser estudadas separadamente. As transições eletrônicas são de ordem 1 eV, as transições vibracionais são de ordem\(10^{-2}eV\) e as transições rotacionais são de ordem\(10^{-3}eV\). Para moléculas complexas, essas mudanças de energia são difíceis de caracterizar, então começamos com o caso simples de uma molécula diatômica.
Rotação quântica
De acordo com a mecânica clássica, a energia de rotação de uma molécula diatômica é dada por
\[E_r = \dfrac{L^2}{2I}, \nonumber \]
onde I é o momento de inércia e L é o momento angular. De acordo com a mecânica quântica, o momento angular rotacional é quantizado:
\[L = \sqrt{l(l + 1)} \hbar (l = 0,1,2,3,...), \nonumber \]
onde l é o número quântico angular orbital. O nível de energia rotacional permitido de uma molécula diatômica é, portanto,
\[E_r = l(l + 1) \dfrac{\hbar^2}{2I} = l(l + 1) \, E_{0r} \, \, (l = 0,1,2,3,...), \nonumber \]
onde a energia rotacional característica de uma molécula é definida como
\[E_{0r} = \dfrac{\hbar^2}{2I}. \nonumber \]
Para uma molécula diatômica, o momento de inércia com massa reduzida\(μ\) é
\[I = \mu r_0^2, \nonumber \]
onde\(r_0\) é a distância total entre os átomos. A diferença de energia entre os níveis rotacionais é, portanto,
\[\Delta E_r = E_{l+1} - E_l = 2(l + 1) \, E_{0r}. \nonumber \]
Um estudo detalhado das transições entre os níveis de energia rotacional provocados pela absorção ou emissão de radiação (a chamada transição de dipolo elétrico) requer que
\[\Delta l = \pm1. \label{delta l} \]
Essa regra, conhecida como regra de seleção, limita as possíveis transições de um estado quântico para outro. A equação\ ref {delta l} é a regra de seleção para transições de energia rotacional. Aplica-se apenas a moléculas diatômicas que têm um momento de dipolo elétrico. Por esse motivo, moléculas simétricas como\(H_2\) e\(N_2\) não experimentam transições de energia rotacional devido à absorção ou emissão de radiação eletromagnética.
Determine os três níveis mais baixos de energia rotacional de uma molécula de cloreto de hidrogênio (\(\ce{HCl}\))).
Estratégia
O cloreto de hidrogênio (\(\ce{HCl}\)) é uma molécula diatômica com uma distância de separação de equilíbrio de 0,127 nm. Os níveis de energia rotacional dependem apenas do momento de inércia I e do número quântico do momento angular orbital\(l\) (neste caso\(l = 0\), 1 e 2). O momento de inércia depende, por sua vez, da distância de separação de equilíbrio (que é dada) e da massa reduzida, que depende das massas dos átomos de H e Cl.
Solução
Primeiro, calculamos a massa reduzida. Se a Partícula 1 é hidrogênio e a Partícula 2 é cloreto, temos
\[\begin{align*} \mu &= \dfrac{m_1m_2}{m_1 + m_2} = \dfrac{(1.0 \, u)(35.4 \, u)}{1.0 \, u + 35.4 \, u} \\[4pt] &= 0.97 \, u = 0.97 \, u \left(\dfrac{931.5 \dfrac{MeV}{c^2}}{1 \, u}\right) \\[4pt] &= 906 \dfrac{MeV}{c^2}. \end{align*} \nonumber \]
A energia de massa restante correspondente é, portanto,
\[\mu c^2 = 9.06 \times 10^8 \, eV \nonumber \]
Isso nos permite calcular a energia característica:
\[ \begin{align*} E_{0r} &= \dfrac{\hbar^2}{2(\mu r_0^2)} = \dfrac{(\hbar c)^2}{2(\mu c^2)r_0^2} \nonumber \\[4pt] &= \dfrac{(197.3 \, eV \cdot nm)^2}{2(9.06 \times 10^8 eV)(0.127 \, nm)^2} \nonumber \\[4pt] &= 1.33 \times 10^{-3} eV. \nonumber \end{align*} \nonumber \]
(Observe como essa expressão é escrita em termos da energia da massa restante. Essa técnica é comum em cálculos físicos modernos.) Os níveis de energia rotacional são dados por
\[E_r = l(l + 1) \dfrac{\hbar^2}{2I} = l(l + 1) E_{0r}, \nonumber \]
onde\(l\) está o número quântico orbital. Os três níveis mais baixos de energia rotacional de uma molécula de HCl são, portanto,
\[\begin{align*} l &= 0:\quad E_r &&= 0 \, eV \, \text{(no rotation)} \\[4pt] l &= 1: \quad E_r &&= 2 \, E_{0r} = 2.66 \times 10^{-3}eV, \\[4pt] l &= 2:\quad E_r &&= 6 \, E_{0r} = 7.99 \times 10^{-3} eV. \end{align*} \nonumber \]
Significância
O espectro rotacional está associado a transições fracas (1/1000 a 1/100 de um eV). Em comparação, a energia de um elétron no estado fundamental do hidrogênio é\(- 13.6 \, eV\).
O que a separação de energia entre as linhas de absorção em um espectro rotacional de uma molécula diatômica lhe diz?
- Responda
-
o momento de inércia
Vibração quântica
O nível de energia vibracional, que é o nível de energia associado à energia vibracional de uma molécula, é mais difícil de estimar do que o nível de energia rotacional. No entanto, podemos estimar esses níveis assumindo que os dois átomos na molécula diatômica estão conectados por uma mola ideal da constante de mola k. A energia potencial deste sistema de molas é
\[U_{osc} = \dfrac{1}{2}k \Delta r^2, \nonumber \]
Onde\(\Delta r\) está uma mudança no “comprimento natural” da molécula ao longo de uma linha que conecta os átomos. Resolver a equação de Schrödinger para esse potencial dá
\[E_n = \left(n + \dfrac{1}{2}\right) \hbar \omega \, (n = 0,1,2,. . .), \nonumber \]
Onde\(\omega\) está a frequência angular natural da vibração e n é o número quântico vibracional. A previsão de que os níveis de energia vibracional estão uniformemente espaçados (\(\Delta E = \hbar \omega\)) acaba sendo boa em energias mais baixas.
Um estudo detalhado das transições entre os níveis de energia vibracional induzidos pela absorção ou emissão de radiação (e especificamente a chamada transição de dipolo elétrico) requer que
\[\Delta n = \pm 1. \label{delta n} \]
A equação\ ref {delta n} representa a regra de seleção para transições de energia vibracional. Como mencionado anteriormente, essa regra se aplica apenas a moléculas diatômicas que têm um momento de dipolo elétrico. As moléculas simétricas não experimentam tais transições.
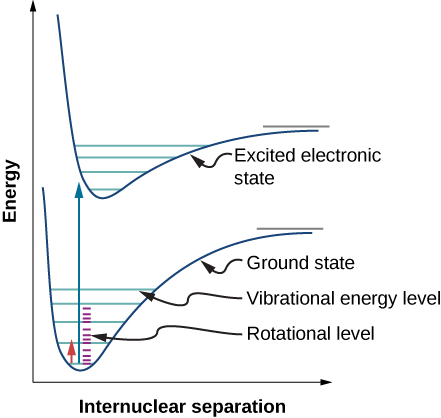
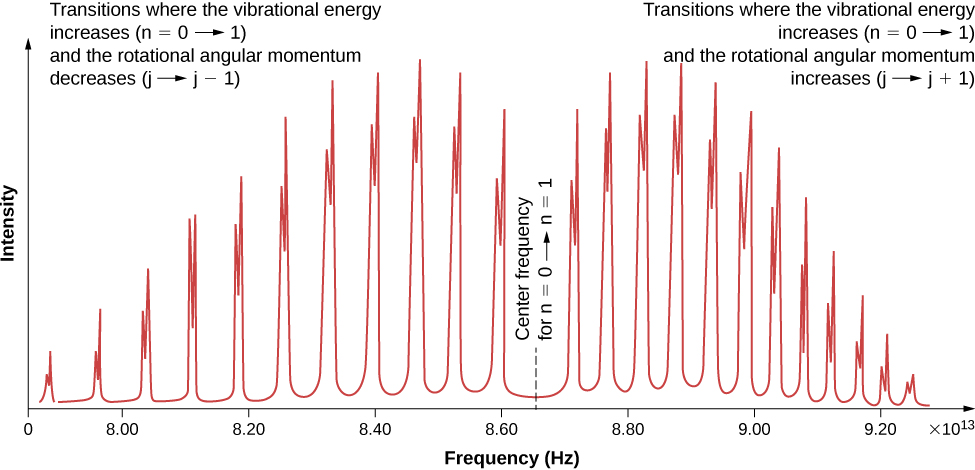
Devido às regras de seleção, a absorção ou emissão de radiação por uma molécula diatômica envolve uma transição nos estados vibracional e rotacional. Especificamente, se o número quântico vibracional (n) mudar em uma unidade, o número quântico rotacional (l) muda em uma unidade. Um diagrama do nível de energia de uma possível transição é dado na Figura\(\PageIndex{1}\). O espectro de absorção para tais transições em cloreto de hidrogênio (HCl) é mostrado na Figura (\ PageIndex {2}\). Os picos de absorção são devidos às transições dos estados vibracional\(n = 0\) para o\(n = 1\) estado vibracional. As diferenças de energia para a faixa de picos à esquerda e à direita são, respectivamente:
(banda direita)
\[ \Delta E_{l \rightarrow l+1} = \hbar \omega + 2(l + 1)E_{0r} = \hbar \omega + 2E_{0r}, \, \hbar \omega + 4E_{0r}, \, \hbar \omega + 6E_{0r}, ... \nonumber \]
(banda esquerda)
\[ \Delta E_{l \rightarrow l-1} = \hbar \omega - 2l E_{0r} = \hbar \omega - 2E_{0r}, \, \hbar \omega - 4E_{0r}, \, \hbar \omega - 6E_{0r}, .... \nonumber \]
O momento de inércia pode então ser determinado a partir do espaçamento de energia entre picos individuais (\(2E_{0r}\)) ou do espaço entre as bandas esquerda e direita (\(4E_{0r}\)). A frequência no centro dessa lacuna é a frequência da vibração.