7.A: Mecânica Quântica (Respostas)
- Page ID
- 183253
Verifique sua compreensão
7.1. \(\displaystyle (3+4i)(3−4i)=9−16i^2=25\)
7.2. \(\displaystyle A=\sqrt{2/L}\)
7.3. \(\displaystyle (1/2−1/π)/2=9%\)
7.4. \(\displaystyle 4.1×10^{−8}eV; 1.1×10^{−5}nm\)
7,5. \(\displaystyle 0.5mω^2x^2ψ(x)∗ψ(x)\)
7.6. Nenhuma. A primeira função tem uma descontinuidade; a segunda função tem valor duplo; e a terceira função diverge, portanto, não é normalizável.
7.7. a. 9,1%;
b. 25%
7.8. a. 295 N/m;
b. 0,277 eV
7.9. \(\displaystyle ⟨x⟩=0\)
7.10. \(\displaystyle L_{proton}/L_{electron}=\sqrt{m_e/m_p}=2.3%\)
Perguntas conceituais
1. \(\displaystyle 1/\sqrt{L}\), onde\(\displaystyle L=length\); 1/L, onde\(\displaystyle L=length\)
3. A função de onda não corresponde diretamente a nenhuma quantidade medida. É uma ferramenta para prever os valores das quantidades físicas.
5. O valor médio da quantidade física para um grande número de partículas com a mesma função de onda.
7. Sim, se sua posição for completamente desconhecida. Sim, se seu momentum for completamente desconhecido.
9. Não. De acordo com o princípio da incerteza, se a incerteza sobre a posição da partícula for pequena, a incerteza sobre seu momento é grande. Da mesma forma, se a incerteza sobre a posição da partícula for grande, a incerteza sobre seu momento é pequena.
11. Não, isso significa que as previsões sobre a partícula (expressas em termos de probabilidades) são independentes do tempo.
13. Não, porque a probabilidade da partícula existir em um intervalo estreito (infinitesimalmente pequeno) na descontinuidade é indefinida.
15. Não. Para um poço quadrado infinito, o espaçamento entre os níveis de energia aumenta com o número quântico n. A menor energia medida corresponde à transição de n = 2 para 1, que é três vezes a energia do estado fundamental. A maior energia medida corresponde a uma transição de\(\displaystyle n=∞\) para 1, que é infinito. (Nota: Mesmo partículas com energias extremamente grandes permanecem ligadas a um poço quadrado infinito — elas nunca podem “escapar”)
17. Não. Essa energia corresponde a\(\displaystyle n=0.25\), mas n deve ser um número inteiro.
19. Porque o menor valor permitido do número quântico n para um oscilador harmônico simples é 0. Não, porque a mecânica quântica e a mecânica clássica concordam apenas no limite do grande nn.
21. Sim, dentro das restrições do princípio da incerteza. Se a partícula oscilante estiver localizada, o momento e, portanto, a energia do oscilador serão distribuídos.
23. duplicando a largura da barreira
25. Não, a força restauradora na partícula nas paredes de um poço quadrado infinito é infinita.
Problemas
27. \(\displaystyle ∣ψ(x)∣^2sin^2ωt\)
29. (a) e (e), podem ser normalizados
31. uma\(\displaystyle A=\sqrt{2α/π}\);.
b.\(\displaystyle probability=29.3%\);
c.\(\displaystyle ⟨x⟩=0⟨x⟩=0\);
d.\(\displaystyle ⟨p⟩=0\);.
e.\(\displaystyle ⟨K⟩=α^2ℏ^2/2m\)
33. uma\(\displaystyle Δp≥2.11×10^{−34}N⋅s\);.
b.\(\displaystyle Δv≥6.31×10^{−8}m\);
c.\(\displaystyle Δv/\sqrt{k_BT/m_α}=5.94×10^{−11}\)
35. \(\displaystyle Δτ≥1.6×10^{−25}s\)
37. uma\(\displaystyle Δf≥1.59MHz\);.
b.\(\displaystyle Δω/ω_0=3.135×10^{−9}\)
39. Realizando os rendimentos dos derivados\(\displaystyle k^2=\frac{ω^2}{c^2}\).
41. Executar as derivadas (como acima) para a função seno fornece um cosseno no lado direito da equação, então a igualdade falha. O mesmo ocorre com a solução de cosseno.
43. \(\displaystyle E=ℏ^2k^2/2m\)
45. \(\displaystyle ℏ^2k^2ℏ\); A partícula tem momento definido e, portanto, momento definido ao quadrado.
47. 9,4 eV, 64%
49. 0,38 mm
51. 1,82 MeV
53. 24,7 mm
55. \(\displaystyle 6.03Å\)
57. uma.
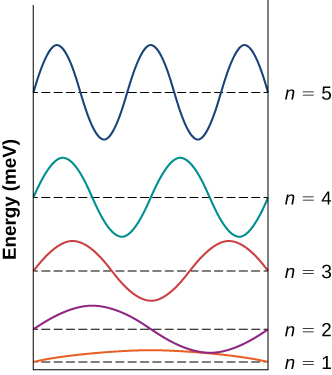
As funções de onda para os estados n=1 a n=5 do elétron em um poço quadrado infinito são mostradas. Cada função é deslocada verticalmente por sua energia, medida em MeV. O estado n=1 é a primeira meia onda da função seno. A função n=2 é a primeira onda completa da função seno. A função n=3 é a primeira onda e meia da função seno. A função n=4 são as duas primeiras ondas da função seno. A função n=5 são as primeiras duas ondas e meia da função seno. ;
b.\(\displaystyle λ_{5→3}=12.9nm,λ_{3→1}=25.8nm,λ_{4→3}=29.4nm\)
59. prova
61. \(\displaystyle 6.662×10^{14}Hz\)
63. \(\displaystyle n≈2.037×10^{30}\)
65. \(\displaystyle ⟨x⟩=0.5mω^2⟨x^2⟩=ℏω/4\);\(\displaystyle ⟨K⟩=⟨E⟩−⟨U⟩=ℏω/4\)
67. prova
69. Uma função complexa da forma,\(\displaystyle Ae^{iϕ}\), satisfaz a equação independente do tempo de Schrdinger. Os operadores de energia cinética e total são lineares, portanto, qualquer combinação linear de tais funções de onda também é uma solução válida para a equação de SchrDinger. Portanto, concluímos que a Equação 7.68 satisfaz a Equação 7.61 e a Equação 7.69 satisfaz a Equação 7.63.
71. a. 4,21%;
b. 0,84%;
c. 0,06%
73. a. 0,13%;
b. perto de 0%
75. 0,38 mm
Problemas adicionais
77. prova
79. a. 4,0%;
b. 1,4%;
c. 4,0%;
d. 1,4%
81. uma\(\displaystyle t=mL^2/h=2.15×10^{26}years\);.
b.\(\displaystyle E_1=1.46×10^{−66}J,K=0.4J\)
83. prova
85. 1,2 N/m
87. 0
Problemas de desafio
89. 19,2 µm; 11,5 µm 19,2 µm; 11,5 µm
91. 3,92%
93. prova


