6.6: Ondas de matéria de De Broglie
- Page ID
- 182970
Ao final desta seção, você poderá:
- Descreva a hipótese de Broglie sobre ondas de matéria
- Explique como a hipótese de Broglie fornece a justificativa para a quantização do momento angular na teoria quântica do átomo de hidrogênio de Bohr
- Descreva o experimento Davisson—Germer
- Interprete a ideia de Broglie sobre ondas de matéria e como elas explicam os fenômenos de difração de elétrons
A fórmula de Compton estabeleceu que uma onda eletromagnética pode se comportar como uma partícula de luz ao interagir com a matéria. Em 1924, Louis de Broglie propôs uma nova hipótese especulativa de que elétrons e outras partículas de matéria podem se comportar como ondas. Hoje, essa ideia é conhecida como a hipótese de de Broglie sobre ondas de matéria. Em 1926, a hipótese de De Broglie, juntamente com a teoria quântica inicial de Bohr, levou ao desenvolvimento de uma nova teoria da mecânica quântica das ondas para descrever a física dos átomos e partículas subatômicas. A mecânica quântica abriu o caminho para novas invenções e tecnologias de engenharia, como o laser e a ressonância magnética (MRI). Essas novas tecnologias impulsionam descobertas em outras ciências, como biologia e química.
De acordo com a hipótese de Broglie, fótons sem massa, bem como partículas massivas, devem satisfazer um conjunto comum de relações que conectam a energia\(E\) com a frequência\(f\) e o momento linear\(p\) com o comprimento de onda\(λ\). Discutimos essas relações para fótons no contexto do efeito de Compton. Estamos recordando-os agora em um contexto mais geral. Qualquer partícula que tenha energia e momento é uma onda de Broglie de frequência\(f\) e comprimento de onda\(\lambda\):
\[ E = h f \label{6.53} \]
\[ \lambda = \frac{h}{p} \label{6.54} \]
Aqui,\(E\) e\(p\) estão, respectivamente, a energia relativista e o momento de uma partícula. As relações de De Broglie geralmente são expressas em termos do vetor\(\vec{k}\) de onda e da frequência da onda\(\omega = 2 \pi f\), como costumamos fazer com as ondas:\(k = 2 \pi / \lambda\)
\ begin {alinhado}
&E=\ hbar\ omega\ label {6,55}\\
&\ vec {p} =\ hbar\ vec {k}\ label {6,56}
\ end {alinhado}
A teoria das ondas nos diz que uma onda carrega sua energia com a velocidade do grupo. Para ondas de matéria, essa velocidade de grupo é a velocidade\(u\) da partícula. Identificando a energia E e o momento p de uma partícula com sua energia relativista\(mc^2\) e seu momento relativístico\(mu\), respectivamente, decorre das relações de de Broglie que ondas de matéria satisfazem a seguinte relação:
\[ \lambda f =\frac{\omega}{k}=\frac{E / \hbar}{p / \hbar}=\frac{E}{p} = \frac{m c^{2}}{m u}=\frac{c^{2}}{u}=\frac{c}{\beta} \label{6.57} \]
onde\(\beta = u/c\). Quando uma partícula não tem massa, temos\(u=c\) e a Equação\ ref {6.57} se torna\(\lambda f = c\).
Calcule o comprimento de onda de de Broglie de:
- uma bola de basquete de 0,65 kg lançada a uma velocidade de 10 m/s,
- um elétron não relativístico com uma energia cinética de 1,0 eV, e
- um elétron relativístico com uma energia cinética de 108 keV.
Estratégia
Usamos a Equação\ ref {6.57} para encontrar o comprimento de onda de Broglie. Quando o problema envolve um objeto não relativista se movendo com uma velocidade não relativista u, como em (a) quando\(\beta=u / c \ll 1\), usamos momento não relativístico p. Quando a aproximação não relativista não pode ser usada, como em (c), devemos usar o momento relativístico\(p=m u=m_{0} \gamma u=E_{0} \gamma \beta/c\), onde a energia de massa restante de uma partícula é\(E_0 = m c^2 \) e\(\gamma\) é o fator de Lorentz\(\gamma=1 / \sqrt{1-\beta^{2}}\). A energia total\(E\) de uma partícula é dada pela Equação\ ref {6.53} e a energia cinética é\(K=E-E_{0}=(\gamma-1) E_{0}\). Quando a energia cinética é conhecida, podemos inverter a Equação 6.4.2 para encontrar o momento
\[ p=\sqrt{\left(E^{2}-E_{0}^{2}\right) / c^{2}}=\sqrt{K\left(K+2 E_{0}\right)} / c \nonumber \]
e substitua na Equação\ ref {6.57} para obter
\[ \lambda=\frac{h}{p}=\frac{h c}{\sqrt{K\left(K+2 E_{0}\right)}} \label{6.58} \]
Dependendo do problema em questão, nessa equação, podemos usar os seguintes valores para hc:
\[ h c=\left(6.626 \times 10^{-34} \: \mathrm{J} \cdot \mathrm{s}\right)\left(2.998 \times 10^{8} \: \mathrm{m} / \mathrm{s}\right)=1.986 \times 10^{-25} \: \mathrm{J} \cdot \mathrm{m}=1.241 \: \mathrm{eV} \cdot \mu \mathrm{m} \nonumber \]
Solução
- Para o basquete, a energia cinética é\[ K=m u^{2} / 2=(0.65 \: \mathrm{kg})(10 \: \mathrm{m} / \mathrm{s})^{2} / 2=32.5 \: \mathrm{J} \nonumber \] e o resto da energia da massa é.\[ E_{0}=m c^{2}=(0.65 \: \mathrm{kg})\left(2.998 \times 10^{8} \: \mathrm{m} / \mathrm{s}\right)^{2}=5.84 \times 10^{16} \: \mathrm{J} \nonumber \] Nós vemos isso\(K /\left(K+E_{0}\right) \ll 1\) e usamos\(p=m u=(0.65 \: \mathrm{kg})(10 \: \mathrm{m} / \mathrm{s})=6.5 \: \mathrm{J} \cdot \mathrm{s} / \mathrm{m} \):\[ \lambda=\frac{h}{p}=\frac{6.626 \times 10^{-34} \: \mathrm{J} \cdot \mathrm{s}}{6.5 \: \mathrm{J} \cdot \mathrm{s} / \mathrm{m}}=1.02 \times 10^{-34} \: \mathrm{m} \nonumber \]
- Para o elétron não relativístico\(K = 1.0 \: eV\),\[ E_{0}=mc^{2}=\left(9.109 \times 10^{-31} \mathrm{kg}\right)\left(2.998 \times 10^{8} \mathrm{m} / \mathrm{s}\right)^{2}=511 \mathrm{keV} \nonumber \] e quando\(K/(K+E_0) = (1/512) \times 10^{-3} \ll 1\), temos, então podemos usar a fórmula não relativista. No entanto, é mais simples aqui usar a Equação\ ref {6.58}:\[ \lambda=\frac{h}{p}=\frac{h c}{\sqrt{K\left(K+2 E_{0}\right)}}=\frac{1.241 \: \mathrm{eV} \cdot \mu \mathrm{m}}{\sqrt{(1.0 \: \mathrm{eV})[1.0 \: \mathrm{eV}+2(511 \: \mathrm{keV})]}}=1.23 \: \mathrm{nm} \nonumber \] Se usarmos momento não relativístico, obteremos o mesmo resultado porque 1 eV é muito menor do que a massa restante do elétron.
- Para um elétron rápido com\(K=108 \: keV\), os efeitos relativísticos não podem ser negligenciados porque sua energia total\(K/E = 108/619\) é\(E = K = E_0 = 108 \: keV + 511 \: keV = 619 \: keV\) e não é desprezível:\[ \lambda=\frac{h}{p}=\frac{h c}{\sqrt{K\left(K+2 E_{0}\right)}}=\frac{1.241 \: \mathrm{eV} \cdot \mu \mathrm{m}}{\sqrt{108 \: \mathrm{keV}[108 \: \mathrm{keV}+2(511 \: \mathrm{keV})]}}=3.55 \: \mathrm{pm} \nonumber \].
Significância
Vemos a partir dessas estimativas que os comprimentos de onda de objetos macroscópicos de De Broglie, como uma bola, são incomensuravelmente pequenos. Portanto, mesmo que existam, não são detectáveis e não afetam o movimento de objetos macroscópicos.
Qual é o comprimento de onda de de Broglie de um próton não relativístico com uma energia cinética de 1,0 eV?
- Responda
-
1,7 pm
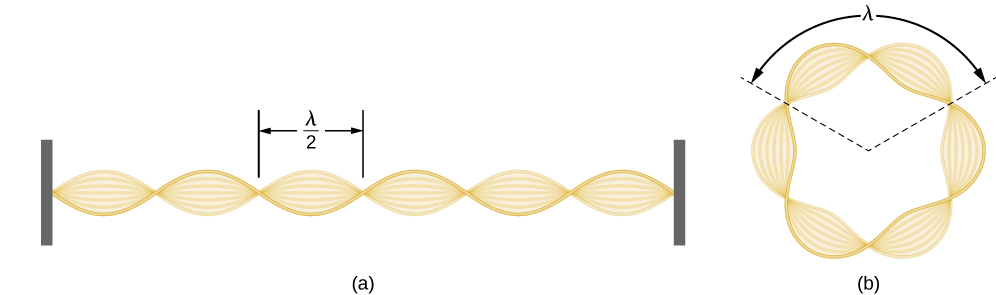
Usando o conceito de onda de matéria eletrônica, de Broglie forneceu uma justificativa para a quantização do momento angular do elétron no átomo de hidrogênio, que foi postulado na teoria quântica de Bohr. A explicação física para a primeira condição de quantização de Bohr surge naturalmente quando assumimos que um elétron em um átomo de hidrogênio se comporta não como uma partícula, mas como uma onda. Para ver com clareza, imagine uma corda de guitarra esticada que está presa nas duas extremidades e vibra em um de seus modos normais. Se o comprimento da corda for l (Figura\(\PageIndex{1}\)), os comprimentos de onda dessas vibrações não podem ser arbitrários, mas devem ser tais que um número inteiro k de meio comprimento de onda\(\lambda/2\) caiba exatamente na distância l entre o acaba. Essa é a condição\(l=k \lambda /2\) para uma onda estacionária em uma corda. Agora, suponha que, em vez de prender a corda nas paredes, dobremos seu comprimento em um círculo e prendemos as pontas uma na outra. Isso produz uma corda circular que vibra nos modos normais, satisfazendo a mesma condição de onda estacionária, mas o número de meias-comprimentos de onda agora deve ser um número par\(k\)\(k=2n\), e o comprimento l agora está conectado ao raio\(r_n\) do círculo. Isso significa que os raios não são arbitrários, mas devem satisfazer a seguinte condição de onda estacionária:
\[ 2 \pi r_{n}=2 n \frac{\lambda}{2} \label{6.59}. \]
Se um elétron na órbita n th de Bohr se move como uma onda, pela Equação\ ref {6.59} seu comprimento de onda deve ser igual\(\lambda = 2 \pi r_n / n\) a. Supondo que a Equação\ ref {6.58} seja válida, a onda eletrônica desse comprimento de onda corresponde ao momento linear do elétron,\(p = h/\lambda = nh / (2 \pi r_n) = n \hbar /r_n\). Em uma órbita circular, portanto, o momento angular do elétron deve ser
\[ L_{n}=r_{n} p=r_{n} \frac{n \hbar}{r_{n}}=n \hbar \label{6.60} . \]
Essa equação é a primeira das condições de quantização de Bohr, dada pela Equação 6.5.6. Fornecer uma explicação física para a condição de quantização de Bohr é um argumento teórico convincente para a existência de ondas de matéria.
Encontre o comprimento de onda de Broglie de um elétron no estado fundamental do hidrogênio.
Estratégia
Combinamos a primeira condição de quantização na Equação\ ref {6.60} com a Equação 6.5.6 e usamos a Equação 6.5.9 para o primeiro raio de Bohr com\(n = 1\).
Solução
Quando\(n=1\) e\(r_n = a_0 = 0.529 \: Å\), a condição de quantização de Bohr fornece\(a_{0} p=1 \cdot \hbar \Rightarrow p=\hbar / a_{0}\). O comprimento de onda do elétron é:
\[ \lambda=h / p = h / \hbar / a_{0} = 2 \pi a_{0} = 2 \pi(0.529 \: Å)=3.324 \: Å .\nonumber \]
Significância
Obtemos o mesmo resultado quando usamos a Equação\ ref {6.58} diretamente.
Encontre o comprimento de onda de Broglie de um elétron no terceiro estado excitado do hidrogênio.
- Responda
-
\(\lambda = 2 \pi n a_0 = 2 (3.324 \: Å) = 6.648 \: Å\)
A confirmação experimental das ondas de matéria veio em 1927, quando C. Davisson e L. Germer realizaram uma série de experimentos de dispersão de elétrons que mostraram claramente que os elétrons se comportam como ondas. Davisson e Germer não montaram seu experimento para confirmar a hipótese de Broglie: A confirmação veio como um subproduto de seus estudos experimentais de rotina de superfícies metálicas sob bombardeio de elétrons.
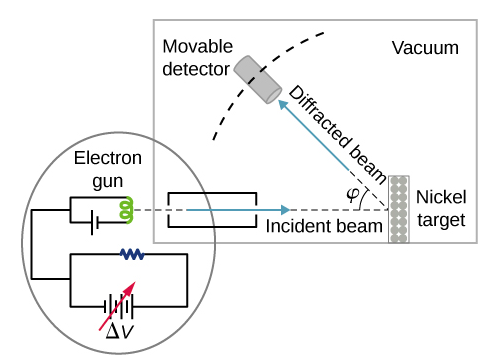
No experimento específico que forneceu a primeira evidência de ondas de elétrons (conhecido hoje como experimento Davisson—Germer), eles estudaram uma superfície de níquel. Sua amostra de níquel foi especialmente preparada em um forno de alta temperatura para mudar sua estrutura policristalina usual para uma forma na qual grandes domínios monocristalinos ocupam o volume. A figura\(\PageIndex{2}\) mostra a configuração experimental. Os elétrons térmicos são liberados de um elemento aquecido (geralmente feito de tungstênio) no canhão de elétrons e acelerados através de uma diferença de potencial ΔV, tornando-se um feixe de elétrons bem colimado produzido por um canhão de elétrons. A energia cinética\(K\) dos elétrons é ajustada selecionando um valor da diferença de potencial no canhão de elétrons. Isso produz um feixe de elétrons com um valor definido de momento linear, de acordo com a conservação de energia:
\[ e \Delta V=K=\frac{p^{2}}{2 m} \Rightarrow p=\sqrt{2 m e \Delta V} \label{6.61} \]
O feixe de elétrons incide na amostra de níquel na direção normal à sua superfície. Na superfície, ele se espalha em várias direções. A intensidade do feixe espalhado em uma direção selecionada φφ é medida por um detector altamente sensível. A posição angular do detector em relação à direção do feixe incidente pode variar de φ=0° a φ=90°. Toda a configuração é fechada em uma câmara de vácuo para evitar colisões de elétrons com moléculas de ar, pois essas colisões térmicas alterariam a energia cinética dos elétrons e não são desejáveis.
Quando o alvo de níquel tem uma forma policristalina com muitos cristais microscópicos orientados aleatoriamente, os elétrons incidentes se espalham por sua superfície em várias direções aleatórias. Como resultado, a intensidade do feixe de elétrons disperso é praticamente a mesma em qualquer direção, semelhante a uma reflexão difusa da luz de uma superfície porosa. No entanto, quando o alvo de níquel tem uma estrutura cristalina regular, a intensidade do feixe de elétrons disperso mostra um máximo claro em um ângulo específico e os resultados mostram um padrão de difração claro (veja a Figura\(\PageIndex{3}\)). Padrões de difração similares formados por raios X espalhados por vários sólidos cristalinos foram estudados em 1912 pelos físicos de pai e filho William H. Bragg e William L. Bragg. A lei de Bragg na cristalografia de raios-X fornece uma conexão entre o comprimento\(\lambda\) de onda da radiação incidente em uma rede cristalina, o espaçamento da rede e a posição do máximo de interferência na radiação difratada (consulte Difração).
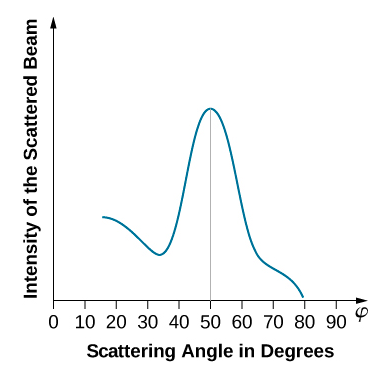
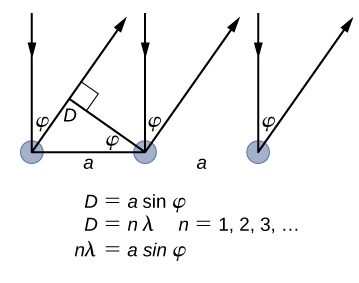
O espaçamento da rede do alvo de Davisson-Germer, determinado com cristalografia de raios-X, foi medido como sendo\(a=2.15 \: Å\). Ao contrário da cristalografia de raios-X, na qual os raios X penetram na amostra, no experimento original de Davisson—Germer, somente os átomos da superfície interagem com o feixe de elétrons incidente. Para a difração de superfície, a intensidade máxima do feixe de elétrons refletido é observada para ângulos de dispersão que satisfazem a condição nλ = a sin φ (veja a Figura\(\PageIndex{4}\)). O máximo de primeira ordem (para n = 1) é medido em um ângulo de dispersão de φ≈ 50° em ΔV≈ 54 V, que fornece o comprimento de onda da radiação incidente como λ= (2,15 Å) sin 50° = 1,64 Å. Por outro lado, um potencial de 54 V acelera os elétrons incidentes em energias cinéticas de K = 54 eV. Seu momentum, calculado a partir da Equação\ ref {6.61}, é\(p = 2.478 \times 10^{−5} \: eV \cdot s/m\). Quando substituímos esse resultado na Equação\ ref {6.58}, o comprimento de onda de Broglie é obtido como
\[ \lambda=\frac{h}{p}=\frac{4.136 \times 10^{-15} \mathrm{eV} \cdot \mathrm{s}}{2.478 \times 10^{-5} \mathrm{eV} \cdot \mathrm{s} / \mathrm{m}}=1.67 \mathrm{Å} \label{6.62}. \]
O mesmo resultado é obtido quando usamos K = 54eV na Equação\ ref {6.61}. A proximidade desse resultado teórico com o valor experimental de Davisson-Germer de λ = 1,64 Å é um argumento convincente para a existência de ondas de matéria de Broglie.
As linhas de difração medidas com elétrons de baixa energia, como as usadas no experimento Davisson—Germer, são bastante amplas (Figura\(\PageIndex{3}\)) porque os elétrons incidentes estão espalhados apenas pela superfície. A resolução das imagens de difração melhora muito quando um feixe de elétrons de alta energia passa por uma fina folha de metal. Isso ocorre porque a imagem de difração é criada pela dispersão de muitos planos cristalinos dentro do volume, e os máximos produzidos na dispersão nos ângulos de Bragg são nítidos (Figura\(\PageIndex{5}\)).

Desde o trabalho de Davisson e Germer, a hipótese de Broglie foi extensivamente testada com várias técnicas experimentais, e a existência de ondas de Broglie foi confirmada para várias partículas elementares. Os nêutrons têm sido usados em experimentos de dispersão para determinar estruturas cristalinas de sólidos a partir de padrões de interferência formados por ondas de matéria de nêutrons. O nêutron tem carga zero e sua massa é comparável à massa de um próton com carga positiva. Tanto os nêutrons quanto os prótons podem ser vistos como ondas de matéria. Portanto, a propriedade de ser uma onda de matéria não é específica para partículas eletricamente carregadas, mas é verdadeira para todas as partículas em movimento. Ondas de matéria de moléculas tão grandes quanto carbono\(C_{60}\) foram medidas. Todos os objetos físicos, pequenos ou grandes, têm uma onda de matéria associada, desde que permaneçam em movimento. O caráter universal das ondas de matéria de Broglie está firmemente estabelecido.
Suponha que um feixe de nêutrons seja usado em um experimento de difração em um sólido cristalino típico. Estime a energia cinética de um nêutron (em eV) no feixe de nêutrons e compare-a com a energia cinética de um gás ideal em equilíbrio à temperatura ambiente.
Estratégia
Assumimos que um espaçamento cristalino típico a é da ordem de 1,0 Å. Para observar um padrão de difração em tal rede, o comprimento de onda λ do nêutron deve estar na mesma ordem de magnitude do espaçamento da rede. Usamos a Equação\ ref {6.61} para encontrar o momento p e a energia cinética K. Para comparar essa energia com a energia\(E_T\) do gás ideal em equilíbrio à temperatura ambiente\(T = 300 \, K\), usamos a relação\(K = 3/2 k_BT\), onde\(k_B = 8.62 \times 10^{-5}eV/K\) está a constante de Boltzmann.
Solução
Avaliamos o pc para compará-lo com a energia de massa restante do nêutron\(E_0 = 940 \, MeV\):
\[p = \frac{h}{\lambda} \Rightarrow pc = \frac{hc}{\lambda} = \frac{1.241 \times 10^{-6}eV \cdot m}{10^{-10}m} = 12.41 \, keV. \nonumber \]
Vemos isso\(p^2c^2 << E_0^2\) e podemos usar a energia cinética não relativista:
\[K = \frac{p^2}{2m_n} = \frac{h^2}{2\lambda^2 m_n} = \frac{(6.63\times 10^{−34}J \cdot s)^2}{(2\times 10^{−20}m^2)(1.66 \times 10^{−27} kg)} = 1.32 \times 10^{−20} J = 82.7 \, meV. \nonumber \]
A energia cinética do gás ideal em equilíbrio a 300 K é:
\[K_T = \frac{3}{2}k_BT = \frac{3}{2} (8.62 \times 10^{-5}eV/K)(300 \, K) = 38.8 \, MeV. \nonumber \]
Vemos que essas energias são da mesma ordem de magnitude.
Significância
Os nêutrons com energias nessa faixa, o que é típico de um gás ideal à temperatura ambiente, são chamados de “nêutrons térmicos”.
Em um supercolisor no CERN, os prótons podem ser acelerados a velocidades de 0,75 c. Quais são seus comprimentos de onda de Broglie nessa velocidade? Quais são suas energias cinéticas?
Estratégia
A energia de massa restante de um próton é\(E_0 = m_0c^2 = (1.672 \times 10^{−27} kg)(2.998 \times 10^8m/s)^2 = 938 \, MeV\). Quando a velocidade do próton é conhecida, temos β = 0,75\(\beta \gamma = 0.75 / \sqrt{1 - 0.75^2} = 1.714\) e. Obtemos o comprimento de onda λλ e a energia cinética K a partir de relações relativísticas.
Solução
\[\lambda = \frac{h}{p} = \frac{hc}{\beta \gamma E_0} = \frac{1.241 \, eV \cdot \mu m}{1.714 (938 \, MeV)} = 0.77 \, fm \nonumber \]
\[K = E_0(\gamma - 1) = 938 \, MeV (1 /\sqrt{1 - 0.75^2} - 1) = 480.1\, MeV \nonumber \]
Significância
Observe que, como um próton é 1835 vezes mais massivo que um elétron, se esse experimento fosse realizado com elétrons, um simples redimensionamento desses resultados nos daria o comprimento de onda do elétron de (1835) 0,77 fm = 1,4 pm e sua energia cinética de 480,1 MeV/1835 = 261,6 keV.
Encontre o comprimento de onda de Broglie e a energia cinética de um elétron livre que viaja a uma velocidade de 0,75 c.
- Responda
-
\(\lambda = 1.417 \, pm; \, K = 261.56 \, keV\)


