6.5: Modelo de Bohr do átomo de hidrogênio

Objetivos de

Ao final desta seção, você poderá:

• Explicar a diferença entre o espectro de absorção e o espectro de emissão da radiação emitida pelos átomos
• Descreva o experimento da folha de ouro de Rutherford e a descoberta do núcleo atômico
• Explicar a estrutura atômica do hidrogênio
• Descreva os postulados da teoria quântica inicial para o átomo de hidrogênio
• Resuma como o modelo quântico do átomo de hidrogênio de Bohr explica o espectro de radiação do hidrogênio atômico

Historicamente, o modelo de Bohr do átomo de hidrogênio é o primeiro modelo de estrutura atômica que explicou corretamente os espectros de radiação do hidrogênio atômico. O modelo tem um lugar especial na história da física porque introduziu uma teoria quântica inicial, que trouxe novos desenvolvimentos no pensamento científico e, posteriormente, culminou no desenvolvimento da mecânica quântica. Para entender as especificidades do modelo de Bohr, devemos primeiro revisar as descobertas do século XIX que motivaram sua formulação.

Figura\(\PageIndex{1}\): No espectro de emissão solar na faixa visível de 380 nm a 710 nm, as linhas de Fraunhofer são observadas como linhas pretas verticais em posições espectrais específicas no espectro contínuo. Instrumentos modernos altamente sensíveis observam milhares dessas linhas.

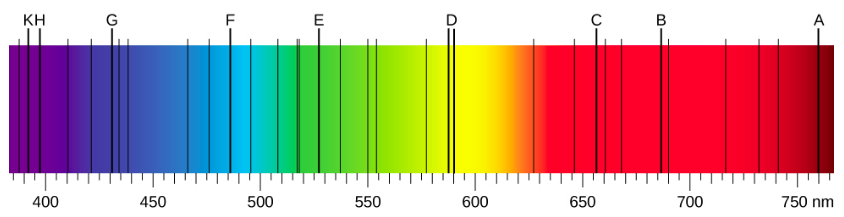
Quando usamos um prisma para analisar a luz branca vinda do sol, várias linhas escuras no espectro solar são observadas (Figura\(\PageIndex{1}\)). As linhas de absorção solar são chamadas de linhas de Fraunhofer em homenagem a Joseph von Fraunhofer, que mediu com precisão seus comprimentos de onda. Durante 1854-1861, Gustav Kirchhoff e Robert Bunsen descobriram que, para os vários elementos químicos, o espectro de emissão linear de um elemento corresponde exatamente ao espectro de absorção da linha. A diferença entre o espectro de absorção e o espectro de emissão é explicada na Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Observação de espectros de linha: (a) configuração para observar linhas de absorção; (b) configuração para observar linhas de emissão. (a) A luz branca passa por um gás frio que está contido em um frasco de vidro. Um prisma é usado para separar os comprimentos de onda da luz passada. No espectro da luz passada, faltam alguns comprimentos de onda, que são vistos como linhas de absorção pretas no espectro contínuo na tela de visualização. (b) Um gás está contido em um tubo de descarga de vidro que tem eletrodos em suas extremidades. Com uma alta diferença de potencial entre os eletrodos, o gás brilha e a luz emitida pelo gás passa pelo prisma que separa seus comprimentos de onda. No espectro da luz emitida, apenas comprimentos de onda específicos estão presentes, que são vistos como linhas de emissão coloridas na tela.

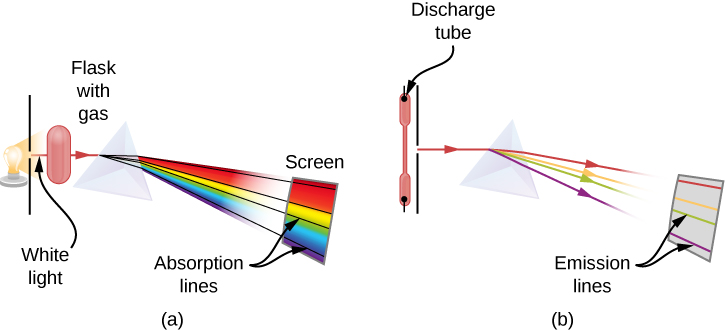
Um espectro de absorção é observado quando a luz passa por um gás. Esse espectro aparece como linhas pretas que ocorrem apenas em determinados comprimentos de onda no fundo do espectro contínuo de luz branca (Figura\(\PageIndex{2}\)). Os comprimentos de onda ausentes nos dizem quais comprimentos de onda da radiação são absorvidos pelo gás. O espectro de emissão é observado quando a luz é emitida por um gás. Esse espectro é visto como linhas coloridas no fundo preto (figuras\(\PageIndex{3}\) e\(\PageIndex{4}\)). As posições das linhas de emissão nos dizem quais comprimentos de onda da radiação são emitidos pelo gás. Cada elemento químico tem seu próprio espectro de emissão característico. Para cada elemento, as posições de suas linhas de emissão são exatamente iguais às posições de suas linhas de absorção. Isso significa que os átomos de um elemento específico absorvem radiação somente em comprimentos de onda específicos e a radiação que não tem esses comprimentos de onda não é absorvida pelo elemento. Isso também significa que a radiação emitida pelos átomos de cada elemento tem exatamente os mesmos comprimentos de onda da radiação que eles absorvem.

Figura\(\PageIndex{3}\): O espectro de emissão do hidrogênio atômico: As posições espectrais das linhas de emissão são características dos átomos de hidrogênio. (crédito: “Merikanto” /Wikimedia Commons)

Figura\(\PageIndex{4}\): O espectro de emissão do ferro atômico: As posições espectrais das linhas de emissão são características dos átomos de ferro.

Os espectros de emissão dos elementos têm estruturas complexas; eles se tornam ainda mais complexos para elementos com números atômicos mais altos. O espectro mais simples, mostrado na Figura\(\PageIndex{4}\), pertence ao átomo de hidrogênio. Apenas quatro linhas são visíveis ao olho humano. Conforme você lê da direita para a esquerda na Figura\(\PageIndex{4}\), essas linhas são: vermelho (656 nm), chamado de\(H-\alpha\) linha; aqua (486 nm), azul (434 nm) e violeta (410 nm). As linhas com comprimentos de onda menores que 400 nm aparecem na parte ultravioleta do espectro (Figura\(\PageIndex{4}\), extrema esquerda) e são invisíveis ao olho humano. Há infinitas linhas espectrais invisíveis na série para hidrogênio.

Uma fórmula empírica para descrever as posições (comprimentos de onda) λ das linhas de emissão de hidrogênio nesta série foi descoberta em 1885 por Johann Balmer. É conhecida como a fórmula do Balmer:

\[ \dfrac{1}{\lambda} = R_H \left( \dfrac{1}{2^2} - \dfrac{1}{n^2}\right). \label{balmer} \]

A constante\(R_H = 1.09737 \times 10^7 m^{-1}\) é chamada de constante de Rydberg para hidrogênio. Na Equação\ ref {balmer}, o inteiro positivo n assume valores\(n = 3, 4,5,6\) para as quatro linhas visíveis nesta série. A série de linhas de emissão dada pela fórmula de Balmer é chamada de série Balmer para hidrogênio. Outras linhas de emissão de hidrogênio descobertas no século XX são descritas pela fórmula de Rydberg, que resume todos os dados experimentais:

\[ \dfrac{1}{\lambda} = R_H \left( \dfrac{1}{n_f^2} - \dfrac{1}{n_i^2}\right)\label{rydberg} \]

onde\(n_i = n_f > n_i\) (em etapas inteiras).

Quando\(n_f = 1\), a série de linhas espectrais é chamada de série Lyman. Quando\(n_f = 2\), a série é chamada de série Balmer e, nesse caso, a fórmula de Rydberg coincide com a fórmula de Balmer (Equação\ ref {balmer}). Quando\(n_f = 3\), a série é chamada de série Paschen. Quando\(n_f = 4\), a série é chamada de série Brackett. Quando\(n_f = 5\), a série é chamada de série Pfund. Quando\(n_f = 6\), temos a série Humphreys. Como você pode imaginar, existem infinitas bandas espectrais no espectro do hidrogênio porque\(n_f\) pode ser qualquer número inteiro positivo.

A fórmula de Rydberg para o hidrogênio fornece as posições exatas das linhas espectrais conforme elas são observadas em laboratório; no entanto, no início do século XX, ninguém conseguiu explicar por que funcionava tão bem. A fórmula de Rydberg permaneceu inexplicável até que o primeiro modelo bem-sucedido do átomo de hidrogênio foi proposto em 1913.

Exemplo\(\PageIndex{1}\): Limits of the Balmer Series

Calcule os comprimentos de onda mais longos e mais curtos da série Balmer.

Estratégia

Podemos usar a fórmula de Balmer (Equação\ ref {balmer}) ou a fórmula de Rydberg (Equação\ ref {rydberg}). O maior comprimento de onda é obtido quando\(1/n_i\) i é maior, que é quando\(n_i = n_f + 1 = 3\), porque\(n_f = 2\) para a série Balmer. O menor comprimento de onda é obtido quando\(1/n_i\) é menor, que é\(1/n_i \rightarrow 0\) quando\(n_i \rightarrow \infty\).

Solução

O limite de ondas longas:

\[ \dfrac{1}{\lambda} = R_H \left( \dfrac{1}{2^2} - \dfrac{1}{3^2}\right) = (1.09737 \times 10^7) \dfrac{1}{m} \left( \dfrac{1}{4} - \dfrac{1}{9}\right) \Rightarrow \lambda = 656.3 \, nm \nonumber \]

O limite de ondas curtas:

\[ \dfrac{1}{\lambda} = R_H \left( \dfrac{1}{2^2} - 0\right) = (1.09737 \times 10^7) \dfrac{1}{m} \left( \dfrac{1}{4} \right) \Rightarrow \lambda = 364.6 \, nm. \nonumber \]

Significância

Observe que há infinitas linhas espectrais situadas entre esses dois limites.

Exercício\(\PageIndex{1}\)

Quais são os limites da série Lyman? Você consegue ver essas linhas espectrais?

Responda

121,5 nm e 91,1 nm; não, essas bandas espectrais estão no ultravioleta

A chave para desvendar o mistério dos espectros atômicos é entender a estrutura atômica. Os cientistas sabem há muito tempo que a matéria é feita de átomos. De acordo com a ciência do século XIX, os átomos são as menores quantidades indivisíveis de matéria. Essa crença científica foi destruída por uma série de experimentos inovadores que provaram a existência de partículas subatômicas, como elétrons, prótons e nêutrons.

O elétron foi descoberto e identificado como a menor quantidade de carga elétrica por J.J. Thomson em 1897 em seus experimentos com raios catódicos, também conhecidos como experimentos com raios β: Um raio β é um feixe de elétrons. Em 1904, Thomson propôs o primeiro modelo de estrutura atômica, conhecido como modelo de “pudim de ameixa”, no qual um átomo consistia em uma matéria desconhecida carregada positivamente com elétrons negativos embutidos nela como ameixas em um pudim. Por volta de 1900, E. Rutherford e, independentemente, Paul Ulrich Villard, classificaram toda radiação conhecida na época como\(\alpha\) - raios,\(β\) - raios e\(\gamma\) - raios (um\(\gamma\) raio X é um feixe de fótons altamente energéticos). Em 1907, Rutherford e Thomas Royds usaram métodos de espectroscopia para mostrar que partículas de\(\alpha\) radiação com carga positiva (chamadas de\(\alpha\) partículas -) são, na verdade, átomos de hélio duplamente ionizados. Em 1909, Rutherford, Ernest Marsden e Hans Geiger usaram\(\alpha\) partículas em seu famoso experimento de dispersão que refutou o modelo de Thomson (veja Momento Linear e Colisões).

No experimento de folha de ouro de Rutherford (também conhecido como experimento Geiger-Marsden), partículas α incidiram em uma fina folha de ouro e foram espalhadas por átomos de ouro dentro da folha (consulte Tipos de colisões). As partículas de saída foram detectadas por uma tela de cintilação de 360° ao redor do alvo dourado (para uma descrição detalhada da configuração experimental, consulte Momentum Linear and Collisions). Quando uma partícula dispersa atingiu a tela, um pequeno flash de luz (cintilação) foi observado naquele local. Ao contar as cintilações observadas em vários ângulos em relação à direção do feixe incidente, os cientistas puderam determinar qual fração das partículas incidentes estava dispersa e qual fração não foi desviada. Se o modelo do pudim de ameixa estivesse correto, não haveria partículas α retroespalhadas. No entanto, os resultados do experimento de Rutherford mostraram que, embora uma fração considerável de partículas α tenha surgido da folha sem se espalhar, como se a folha não estivesse no caminho, uma fração significativa das partículas α foi retroespalhada em direção à fonte. Esse tipo de resultado só foi possível quando a maior parte da massa e toda a carga positiva do átomo de ouro estavam concentradas em um pequeno espaço dentro do átomo.

Em 1911, Rutherford propôs um modelo nuclear do átomo. No modelo de Rutherford, um átomo continha um núcleo carregado positivamente de tamanho insignificante, quase como um ponto, mas incluía quase toda a massa do átomo. O átomo também continha elétrons negativos que estavam localizados dentro do átomo, mas relativamente distantes do núcleo. Dez anos depois, Rutherford cunhou o nome próton para o núcleo de hidrogênio e o nome nêutron para uma hipotética partícula eletricamente neutra que mediaria a ligação de prótons positivos no núcleo (o nêutron foi descoberto em 1932 por James Chadwick). A Rutherford é creditada com a descoberta do núcleo atômico; no entanto, o modelo Rutherford da estrutura atômica não explica a fórmula de Rydberg para as linhas de emissão de hidrogênio.

O modelo de Bohr do átomo de hidrogênio, proposto por Niels Bohr em 1913, foi o primeiro modelo quântico que explicou corretamente o espectro de emissão de hidrogênio. O modelo de Bohr combina a mecânica clássica do movimento planetário com o conceito quântico de fótons. Depois que Rutherford estabeleceu a existência do núcleo atômico, a intuição de Bohr de que o elétron negativo no átomo de hidrogênio deve girar em torno do núcleo positivo tornou-se uma consequência lógica da lei da atração eletrostática da distância quadrada inversa. Lembre-se de que a lei de Coulomb que descreve a atração entre duas cargas opostas tem uma forma semelhante à lei universal da gravitação de Newton, no sentido de que a força gravitacional e a força eletrostática estão diminuindo como\(1/r^2\), onde r é a distância de separação entre os corpos . Da mesma forma que a Terra gira em torno do sol, o elétron negativo no átomo de hidrogênio pode girar em torno do núcleo positivo. No entanto, uma carga acelerada irradia sua energia. Classicamente, se o elétron se movesse ao redor do núcleo de forma planetária, ele estaria passando por uma aceleração centrípeta e, portanto, estaria irradiando energia que o faria descer em espiral até o núcleo. Esse átomo de hidrogênio planetário não seria estável, o que é contrário ao que sabemos sobre átomos de hidrogênio comuns que não se desintegram. Além disso, o movimento clássico do elétron não é capaz de explicar o espectro discreto de emissão do hidrogênio.

Para contornar essas duas dificuldades, Bohr propôs os seguintes três postulados do modelo de Bohr:

1. O elétron negativo se move ao redor do núcleo positivo (próton) em uma órbita circular. Todas as órbitas dos elétrons estão centradas no núcleo. Nem todas as órbitas classicamente possíveis estão disponíveis para um elétron ligado ao núcleo.
2. As órbitas eletrônicas permitidas satisfazem a primeira condição de quantização: Na enésima órbita, o momento angular\(L_n\) do elétron pode ter apenas valores discretos:\[L_n = n\hbar, \, where \, n = 1,2,3, . . . \nonumber \] Este postulado diz que o momento angular do elétron é quantizado. Denotada por\(r_n\) e\(v_n\), respectivamente, pelo raio da enésima órbita e pela velocidade do elétron nela, a primeira condição de quantização pode ser expressa explicitamente como\[m_ev_nr_n = n\hbar. \label{6.34} \]
3. É permitido que um elétron faça transições de uma órbita onde está sua energia\(E_n\) para outra órbita onde está sua energia\(E_m\). Quando um átomo absorve um fóton, o elétron faz uma transição para uma órbita de maior energia. Quando um átomo emite um fóton, o elétron transita para uma órbita de baixa energia. As transições eletrônicas com a absorção simultânea de fótons ou emissão de fótons ocorrem instantaneamente. As transições eletrônicas permitidas satisfazem a segunda condição de quantização:\[hf = |E_n - E_m| \nonumber \] onde\(hf\) está a energia de um fóton emitido ou absorvido com frequência\(f\). A segunda condição de quantização afirma que a mudança de energia de um elétron no átomo de hidrogênio é quantizada.

Esses três postulados da teoria quântica inicial do átomo de hidrogênio nos permitem derivar não apenas a fórmula de Rydberg, mas também o valor da constante de Rydberg e outras propriedades importantes do átomo de hidrogênio, como seus níveis de energia, sua energia de ionização e os tamanhos das órbitas de elétrons. Observe que no modelo de Bohr, junto com dois postulados de quantização não clássicos, também temos a descrição clássica do elétron como uma partícula que está sujeita à força de Coulomb, e seu movimento deve obedecer às leis do movimento de Newton. O átomo de hidrogênio, como um sistema isolado, deve obedecer às leis de conservação de energia e momento da maneira que conhecemos da física clássica. Tendo esse referencial teórico em mente, estamos prontos para prosseguir com nossa análise.

Órbitas eletrônicas

Para obter o tamanho\(r_n\) do elétron na órbita e a velocidade do elétron\(v_n\) nela, recorremos à mecânica newtoniana. Como uma partícula carregada, o elétron experimenta uma atração eletrostática em direção ao núcleo carregado positivamente no centro de sua órbita circular. Essa tração eletrostática é a força centrípeta que faz com que o elétron se mova em um círculo ao redor do núcleo. Portanto, a magnitude da força centrípeta é identificada com a magnitude da força eletrostática:

\[ \dfrac{m_ev_n^2}{r_n} = \dfrac{1}{4\pi \epsilon_0} \dfrac{e^2}{r_n^2}. \label{6.36} \]

Aqui,\(e\) indica o valor da carga elementar. O elétron negativo e o próton positivo têm o mesmo valor de carga,

\[|q| = e. \nonumber \]

Quando a Equação\ ref {6.36} é combinada com a primeira condição de quantização dada pela Equação\ ref {6.34}, podemos resolver para a velocidade,\(v_n\), e para o raio,\(r_n\):

\[v_n = \dfrac{1}{4\pi \epsilon_0} \dfrac{e^2}{\hbar} \dfrac{1}{n} \label{6.37} \]

\[r_n = 4\pi \epsilon_0 \dfrac{\hbar^2}{m_ee^2}n^2. \label{6.38} \]

Observe que esses resultados nos dizem que a velocidade do elétron, bem como o raio de sua órbita, dependem apenas do índice n que enumera a órbita porque todas as outras quantidades nas equações anteriores são constantes fundamentais. Vemos na Equação\ ref {6.38} que o tamanho da órbita cresce como o quadrado de n. Isso significa que a segunda órbita é quatro vezes maior que a primeira órbita, e a terceira órbita é nove vezes maior que a primeira órbita, e assim por diante. Também vemos na Equação\ ref {6.37} que a velocidade do elétron na órbita diminui à medida que o tamanho da órbita aumenta. A velocidade do elétron é maior na primeira órbita de Bohr, para\(n = 1\), que é a órbita mais próxima do núcleo. O raio da primeira órbita de Bohr é chamado de raio de Bohr do hidrogênio, denotado como\(a_0\). Seu valor é obtido configurando\(n = 1\) na Equação\ ref {6.38}:

\[a_0 = 4\pi \epsilon_0 \dfrac{\hbar^2}{m_ee^2} = 5.29 \times 10^{-11} m = 0.529\space Å. \nonumber \]

Podemos substituir\(a_0\) na Equação\ ref {6.38} para expressar o raio da enésima órbita em termos de\(a_0\):

\[r_n = a_0n^2. \label{6.40} \]

Esse resultado significa que as órbitas de elétrons no átomo de hidrogênio são quantizadas porque o raio orbital assume apenas valores específicos de\(a_0\)\(4a_0\)\(9a_0\),,,\(16a_0\)... dados pela Equação\ ref {6.40}, e nenhum outro valor é permitido.

Energias eletrônicas

A energia total\(E_n\) de um elétron na enésima órbita é a soma de sua energia cinética\(K_n\) e sua energia potencial eletrostática\(U_n\). Utilizando a Equação\ ref {6.37}, descobrimos que

\[K_n = \dfrac{1}{2}m_ev_n^2 = \dfrac{1}{32\pi^2 \epsilon^2} \dfrac{m_ee^4}{\hbar^2} \dfrac{1}{n^2}. \label{6.41} \]

Lembre-se de que a energia potencial eletrostática de interação entre duas cargas\(q_1\) e\(q_2\) que estão separadas por uma distância\(r_{12}\) é\((1/4\pi \epsilon_0)q_1q_2/r_{12}\). Aqui,\(q_1 = +e\) está a carga do núcleo no átomo de hidrogênio (a carga do próton),\(q_2 = -e\) é a carga do elétron e\(r_{12} = r_n\) é o raio da enésima órbita. Agora usamos a Equação\ ref {6.38} para encontrar a energia potencial do elétron:

\[U_n = - \dfrac{1}{4\pi \epsilon_0} \dfrac{e^2}{r_n} = - \dfrac{1}{16\pi^2 \epsilon_0^2} \dfrac{m_ee^4}{\hbar^2} \dfrac{1}{n^2}. \label{6.42} \]

A energia total do elétron é a soma da Equação\ ref {6.41} e da Equação\ ref {6.42}:

\[E_n = K_n + U_n = - \dfrac{1}{32\pi^2 \epsilon_0^2} \dfrac{m_ee^4}{\hbar^2} \dfrac{1}{n^2}. \label{6.43} \]

Observe que a energia depende apenas do índice n porque os símbolos restantes na Equação\ ref {6.43} são constantes físicas. O valor do fator constante na Equação\ ref {6,43} é

\[E_0 = \dfrac{1}{32\pi^2 \epsilon_0^2} \dfrac{m_ee^4}{\hbar^2} = \dfrac{1}{8\epsilon_0^2} \dfrac{m_ee^4}{h^2} = 2.17 \times 10^{-18} J = 13.6 \, eV. \label{6.44} \]

É conveniente expressar a energia do elétron na órbita n th em termos dessa energia, como

\[E_n = -E_0 \dfrac{1}{n^2}. \label{6.45} \]

Agora podemos ver que as energias eletrônicas no átomo de hidrogênio são quantizadas porque elas podem ter apenas valores discretos\(-E_0, \, -E_0/4, \, -E_0/9, \, -E_0/16, . . . \) dados pela Equação\ ref {6.45}, e nenhum outro valor de energia é permitido. Esse conjunto de energias eletrônicas permitidas é chamado de espectro de energia do hidrogênio (Figura\(\PageIndex{5}\)). O índice n que enumera os níveis de energia no modelo de Bohr é chamado de número quântico de energia. Identificamos a energia do elétron dentro do átomo de hidrogênio com a energia do átomo de hidrogênio. Observe que o menor valor de energia é obtido para\(n = 1\), então o átomo de hidrogênio não pode ter energia menor do que isso. Esse menor valor da energia eletrônica no átomo de hidrogênio é chamado de energia do estado fundamental do átomo de hidrogênio e seu valor é

\[E_1 = −E_0 = −13.6 \, eV. \label{6.46} \]

O átomo de hidrogênio pode ter outras energias superiores ao estado fundamental. Esses estados de energia superior são conhecidos como estados de energia excitada de um átomo de hidrogênio.

Figura\(\PageIndex{5}\): O espectro de energia do átomo de hidrogênio. Os níveis de energia (linhas horizontais) representam os estados ligados de um elétron no átomo. Há apenas um estado fundamental, n=1, n=1 e estados excitados quantizados infinitos. Os estados são enumerados pelo número quântico n = 1,2,3,4,... As linhas verticais ilustram as transições eletrônicas permitidas entre os estados. As setas para baixo ilustram transições com a emissão de um fóton com comprimento de onda na banda espectral indicada.

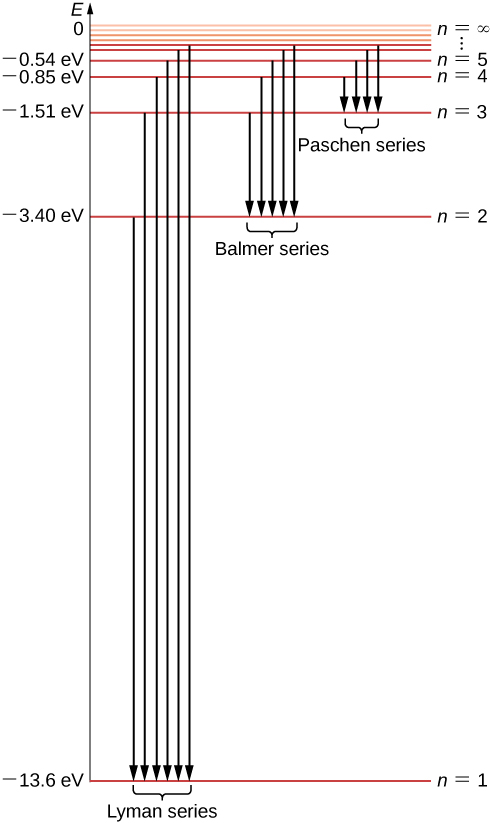
Há apenas um estado fundamental, mas há infinitos estados excitados porque há infinitos valores de n na Equação\ ref {6.45}. Dizemos que o elétron está no “primeiro estado existente” quando sua energia está\(E_n\) (quando\(n = 2\)), o segundo estado excitado quando sua energia está\(E_3\) (quando\(n = 3\)) e, em geral, no n ésimo estado existente quando sua energia está\(E_n + 1\). Não existe o estado de excitação mais elevado de todos; no entanto, há um limite para a sequência de estados excitados. Se continuarmos aumentando\(n\) na Equação\ ref {6.45}, descobrimos que o limite é\(- lim_{n \rightarrow \infty} \, E_0/n^2 = 0\). Nesse limite, o elétron não está mais ligado ao núcleo, mas se torna um elétron livre. Um elétron permanece ligado ao átomo de hidrogênio enquanto sua energia for negativa. Um elétron que orbita o núcleo na primeira órbita de Bohr, mais próximo do núcleo, está no estado fundamental, onde sua energia tem o menor valor. No estado fundamental, o elétron está mais fortemente ligado ao núcleo e sua energia é dada pela Equação\ ref {6.46}. Se quisermos remover esse elétron do átomo, devemos fornecê-lo com energia suficiente\(E_{\infty}\), para pelo menos equilibrar sua energia fundamental\(E_1\):

\[E_{\infty} + E_1 = 0 \Rightarrow E_{\infty} = - E_1 = - (- E_0) = E_0 = 13.6 \, eV. \label{6.47} \]

A energia necessária para remover o elétron do átomo é chamada de energia de ionização. A energia\(E_{\infty}\) de ionização necessária para remover o elétron da primeira órbita de Bohr é chamada de limite de ionização do átomo de hidrogênio. O limite de ionização na Equação\ ref {6.47} que obtemos no modelo de Bohr concorda com o valor experimental.

Linhas de emissão espectral de hidrogênio

Para obter os comprimentos de onda da radiação emitida quando um elétron faz uma transição da enésima órbita para a enésima órbita, usamos a segunda das condições de quantização de Bohr e a Equação\ ref {6.45} para energias. A emissão de energia do átomo só pode ocorrer quando um elétron faz a transição de um estado excitado para um estado de baixa energia. No decorrer dessa transição, o fóton emitido leva embora a diferença de energias entre os estados envolvidos na transição. A transição não pode ir na outra direção porque a energia de um fóton não pode ser negativa, o que significa que, para emissão, devemos ter\(E_n > E_m\)\(n > m\) e. Portanto, o terceiro dos postulados de Bohr dá

\[\begin{align} hf &= |E_n - E_m| \nonumber \\[4pt] &= E_n - E_m \nonumber \\[4pt] &= -E_0 \dfrac{1}{n^2} + E_m \dfrac{1}{m^2} \nonumber \\[4pt] &= E_0 \left( \dfrac{1}{m^2} - \dfrac{1}{n^2} \right). \label{6.48} \end{align} \]

Agora expressamos a energia do fóton em termos de seu comprimento de onda e dividimos os dois lados da Equação\ ref {6.48} por\(hc\).\(hf = hc/\lambda\) O resultado é

\[ \dfrac{1}{\lambda} = \dfrac{E_0}{hc} \left( \dfrac{1}{m^2} - \dfrac{1}{n^2} \right). \label{6.49} \]

O valor da constante nessa equação é

\[\dfrac{E_0}{hc} = \dfrac{13.6 \, eV}{(4.136 \times 10^{-15} eV \cdot s)(2.997 \times 10^8 m/s)} = 1.097 \times 10^7 \dfrac{1}{m}. \label{6.50} \]

Esse valor é exatamente a constante de Rydberg\(R_H\) na fórmula heurística de Rydberg Equation\ ref {rydberg}. Na verdade, a Equação\ ref {6,49} é idêntica à fórmula de Rydberg, porque para um determinado m, temos\(n = m + 1, \, m + 2, . . .\). Dessa forma, o modelo quântico de Bohr do átomo de hidrogênio nos permite derivar a constante experimental de Rydberg dos primeiros princípios e expressá-la em termos de constantes fundamentais. As transições entre as órbitas eletrônicas permitidas são ilustradas na Figura\(\PageIndex{5}\).

Podemos repetir os mesmos passos que levaram à Equação\ ref {6.49} para obter o comprimento de onda da radiação absorvida; isso novamente fornece a Equação\ ref {6.49}, mas desta vez para as posições das linhas de absorção no espectro de absorção do hidrogênio. A única diferença é que, para absorção, o número quântico\(m\) é o índice da órbita ocupada pelo elétron antes da transição (órbita de baixa energia) e o número quântico\(n\) é o índice da órbita para a qual o elétron faz a transição (órbita de maior energia). A diferença entre as energias dos elétrons nessas duas órbitas é a energia do fóton absorvido.

Exemplo\(\PageIndex{2}\): Size and Ionization Energy of the Hydrogen Atom in an Excited State

Se um átomo de hidrogênio no estado fundamental absorve um fóton de 93,7 nm, correspondente a uma linha de transição na série Lyman, como isso afeta a energia e o tamanho do átomo? Quanta energia é necessária para ionizar o átomo quando ele está nesse estado excitado? Dê suas respostas em unidades absolutas e em relação ao estado fundamental.

Estratégia

Antes da absorção, o átomo está em seu estado fundamental. Isso significa que a transição do elétron ocorre da órbita\(m = 1\) para uma parte superior da órbita. Primeiro, devemos determinar nn para o comprimento de onda absorvido\(\lambda = 93.7 \, nm\). Então, podemos usar a Equação\ ref {6.45} para encontrar a energia\(E_n\) do estado excitado e sua energia\(E_{\infty,n}\) de ionização e usar a Equação\ ref {6.40} para encontrar o raio\(r_n\) do átomo no estado excitado. Para estimar n, usamos a Equação\ ref {6.49}.

Solução

Substitua\(m = 1\) e λ = 93,7 nm na Equação\ ref {6,49} e resolva por n. Você não deve esperar obter uma resposta inteira perfeita devido a erros de arredondamento, mas sua resposta será próxima de um inteiro e você pode estimar n tomando a parte integral de sua resposta:

\[ \begin{align*} \dfrac{1}{\lambda} &= R_H \left( \dfrac{1}{1^1} - \dfrac{1}{n^2}\right) \\[4pt] \Rightarrow n &= \dfrac{1}{\sqrt{1 - \dfrac{1}{\lambda R_H}}} \\[4pt] &= \dfrac{1}{\sqrt{1 - \dfrac{1}{(93.7 \times 10^{−9}m)(1.097 \times 10^7 m^{−1})}}} \\[4pt] &= 6.07 \\[4pt] \Rightarrow n &= 6. \end{align*} \]

O raio da\(n = 6\) órbita é

\[r_n = a_0n^2= a_06^2 = 36a_0 = 36(0.529 \times 10^{−10} \, m) = 19.04 \times 10^{−10}\space m ≅ 19.0 \, Å. \nonumber \]

Assim, depois de absorver o fóton de 93,7 nm, o tamanho do átomo de hidrogênio no\(n = 6\) estado excitado é 36 vezes maior do que antes da absorção, quando o átomo estava no estado fundamental. A energia do quinto estado excitado (\(n = 6\)) é:

\[E_n = - \dfrac{E_0}{n^2} = - \dfrac{E_0}{6^2} = - \dfrac{E_0}{36} = - \dfrac{13.6 \, eV}{36} ≅ − 0.378 \, eV. \nonumber \]

Depois de absorver o fóton de 93,7 nm, a energia do átomo de hidrogênio é maior do que era antes da absorção. A ionização do átomo quando ele está no quinto estado excitado (\(n = 6\)) requer 36 vezes menos energia do que a necessária quando o átomo está no estado fundamental:

\[E_{\infty,6} = -E_6 = -(-0.378 \, eV) = 0.378 \, eV. \nonumber \]

Significância

Podemos analisar qualquer linha espectral no espectro do hidrogênio da mesma forma. Assim, as medições experimentais das linhas espectrais nos fornecem informações sobre a estrutura atômica do átomo de hidrogênio.

Exercício\(\PageIndex{2}\)

Quando um elétron em um átomo de hidrogênio está no primeiro estado excitado, que previsão o modelo de Bohr dá sobre sua velocidade orbital e energia cinética? Qual é a magnitude de seu momento angular orbital?

Responda

\(v_2 = 1.1 \times 10^6 m/s ≅0.0036 \, c;\)

\(L_2 = 2\hbar K_2 = 3.4 \, eV\)

O modelo de Bohr do átomo de hidrogênio também prevê corretamente os espectros de alguns íons semelhantes ao hidrogênio. Íons semelhantes ao hidrogênio são átomos de elementos com um número atômico Z maior que um (\(Z = 1\)para hidrogênio), mas com todos os elétrons removidos, exceto um. Por exemplo, um átomo de hélio eletricamente neutro tem um número atômico\(Z = 2\). Isso significa que ele tem dois elétrons orbitando o núcleo com uma carga de\(q = +Ze\). Quando um dos elétrons em órbita é removido do átomo de hélio (dizemos, quando o átomo de hélio é ionizado individualmente), o que resta é uma estrutura atômica semelhante ao hidrogênio, onde o elétron restante orbita o núcleo com uma carga de\(q = +Ze\). Esse tipo de situação é descrito pelo modelo de Bohr. Supondo que a carga do núcleo não seja\(+e\) mas\(+Ze\), podemos repetir todas as etapas, começando com a Equação\ ref {6.36}, para obter os resultados para um íon semelhante ao hidrogênio:

\[r_n = \dfrac{a_0}{Z}n^2 \label{6.51} \]

onde\(a_0\) está a órbita de Bohr do hidrogênio, e

\[E_n = -Z^2E_0 \dfrac{1}{n^2} \label{6.52} \]

onde\(E_0\) está o limite de ionização de um átomo de hidrogênio. Essas equações são boas aproximações, desde que o número atômico Z não seja muito grande.

O modelo de Bohr é importante porque foi o primeiro modelo a postular a quantização de órbitas de elétrons em átomos. Assim, representa uma teoria quântica inicial que deu início ao desenvolvimento da teoria quântica moderna. Ele introduziu o conceito de um número quântico para descrever estados atômicos. A limitação da teoria quântica inicial é que ela não pode descrever átomos nos quais o número de elétrons orbitando o núcleo seja maior que um. O modelo Bohr de hidrogênio é um modelo semi-clássico porque combina o conceito clássico de órbitas de elétrons com o novo conceito de quantização. O notável sucesso desse modelo levou muitos físicos a buscar uma explicação de por que tal modelo deveria funcionar e a buscar uma compreensão da física por trás dos postulados da teoria quântica primitiva. Essa busca trouxe o início de um conceito inteiramente novo de “ondas de matéria”.