6.4: O efeito Compton
- Page ID
- 182954
Ao final desta seção, você poderá:
- Descreva o experimento de Compton
- Explique a mudança de comprimento de onda de Compton
- Descreva como experimentos com raios-X confirmam a natureza das partículas da radiação
Duas das ideias influentes de Einstein introduzidas em 1905 foram a teoria da relatividade especial e o conceito de um quantum de luz, que agora chamamos de fóton. Além de 1905, Einstein foi mais longe ao sugerir que as ondas eletromagnéticas de propagação livre consistiam em fótons que são partículas de luz no mesmo sentido que elétrons ou outras partículas massivas são partículas de matéria. Um feixe de luz monocromática de comprimento de onda\(\lambda\) (ou equivalente, de frequência\(f\)) pode ser visto como uma onda clássica ou como uma coleção de fótons que viajam no vácuo com uma velocidade\(c\) (a velocidade da luz) e todos carregando a mesma energia,\(E_f = hf\). Essa ideia se mostrou útil para explicar as interações da luz com partículas de matéria.
Momento de um fóton
Ao contrário de uma partícula de matéria que é caracterizada por sua massa restante\(m_0\), um fóton não tem massa. No vácuo, diferentemente de uma partícula de matéria que pode variar sua velocidade, mas não pode atingir a velocidade da luz, um fóton viaja a apenas uma velocidade, que é exatamente a velocidade da luz. Do ponto de vista da mecânica clássica newtoniana, essas duas características implicam que um fóton não deveria existir. Por exemplo, como podemos encontrar o momento linear ou a energia cinética de um corpo cuja massa é zero? Esse aparente paradoxo desaparece se descrevermos um fóton como uma partícula relativista. De acordo com a teoria da relatividade especial, qualquer partícula na natureza obedece à equação da energia relativista
\[E^2 = p^2c^2 + m_0^2c^4. \label{6.17} \]
Essa relação também pode ser aplicada a um fóton. Na Equação\ ref {6.17},\(E\) é a energia total de uma partícula,\(p\) é seu momento linear e\(m_0\) é sua massa restante. Para um fóton, simplesmente\(m_0 = 0\) definimos a Equação\ ref {6.17}, que leva à expressão do momento\(p_f\) de um fóton
\[p_f = \dfrac{E_f}{c}. \label{6.18} \]
Aqui, a energia do fóton\(E_f\) é a mesma de um quantum de frequência de luz\(f\), que introduzimos para explicar o efeito fotoelétrico:
\[E_f = hf = \dfrac{hc}{\lambda}. \label{6.19} \]
A relação de onda que conecta a frequência\(f\) com o comprimento de onda\(λ\) e a velocidade\(c\) também vale para os fótons:
\[\lambda f = c \label{6.20} \]
Portanto, um fóton pode ser caracterizado de forma equivalente por sua energia e comprimento de onda ou por sua frequência e momento. As equações\ ref {6.19} e\ ref {6.20} podem ser combinadas na relação explícita entre o momento de um fóton e seu comprimento de onda:
\[p_f = \dfrac{h}{\lambda}. \label{6.21} \]
Observe que essa equação nos fornece apenas a magnitude do momento do fóton e não contém informações sobre a direção na qual o fóton está se movendo. Para incluir a direção, é comum escrever o momento do fóton como um vetor:
\[\vec{p}_f = \hbar \vec{l}. \label{6.22} \]
Na Equação\ ref {6,22},\(\hbar = h/2\pi\) está a constante de Planck reduzida (pronunciada “h-bar”), que é apenas a constante de Planck dividida pelo fator\(2\pi\). O vetor\(\vec{l}\) é chamado de “vetor de onda” ou vetor de propagação (a direção na qual um fóton está se movendo). O vetor de propagação mostra a direção do vetor de momento linear do fóton. A magnitude do vetor de onda é
\[k = |\vec{k}| = 2\pi /\lambda \nonumber \]
e é chamado de número da onda. Observe que essa equação não introduz nenhuma nova física. Podemos verificar que a magnitude do vetor na Equação\ ref {6.22} é a mesma dada pela Equação\ ref {6.18}.
O efeito Compton
O efeito Compton é o termo usado para um resultado incomum observado quando os raios X estão espalhados em alguns materiais. Pela teoria clássica, quando uma onda eletromagnética é dispersa pelos átomos, espera-se que o comprimento de onda da radiação dispersa seja o mesmo que o comprimento de onda da radiação incidente. Ao contrário dessa previsão da física clássica, as observações mostram que quando os raios X são espalhados por alguns materiais, como grafite, os raios X dispersos têm comprimentos de onda diferentes do comprimento de onda dos raios X incidentes. Esse fenômeno classicamente inexplicável foi estudado experimentalmente por Arthur H. Compton e seus colaboradores, e Compton deu sua explicação em 1923.
Para explicar a mudança nos comprimentos de onda medidos no experimento, Compton usou a ideia de Einstein sobre a luz como uma partícula. O efeito Compton tem um lugar muito importante na história da física porque mostra que a radiação eletromagnética não pode ser explicada como um fenômeno puramente ondulatório. A explicação do efeito Compton deu um argumento convincente à comunidade física de que as ondas eletromagnéticas podem de fato se comportar como um fluxo de fótons, o que colocou o conceito de fóton em terreno firme.
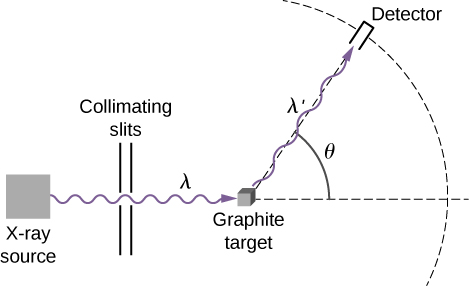
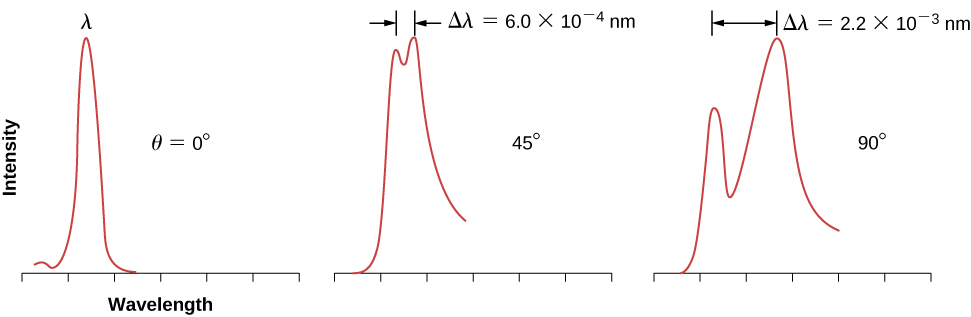
Os esquemas da configuração experimental de Compton são mostrados na Figura\(\PageIndex{1}\). A ideia do experimento é simples: raios-X monocromáticos com comprimento de onda\(λ\) incidem em uma amostra de grafite (o “alvo”), onde interagem com átomos dentro da amostra; posteriormente, emergem como raios X dispersos com comprimento de onda\(λ'\). Um detector colocado atrás do alvo pode medir a intensidade da radiação espalhada em qualquer direção em\(θ\) relação à direção do feixe de raios-X incidente. Esse ângulo de dispersão\(θ\),, é o ângulo entre a direção do feixe disperso e a direção do feixe incidente. Neste experimento, sabemos a intensidade e o comprimento\(λ\) de onda do feixe de entrada (incidente); e para um determinado ângulo de dispersão\(θ\), medimos a intensidade e o comprimento\(λ'\) de onda do feixe de saída (disperso). Os resultados típicos dessas medições são mostrados na Figura\(\PageIndex{2}\), onde o\(x\) eixo -é o comprimento de onda dos raios X dispersos e o\(y\) eixo -é a intensidade dos raios X dispersos, medidos para diferentes ângulos de dispersão (indicados nos gráficos). Para todos os ângulos de dispersão (exceto para\(θ=0°\)), medimos dois picos de intensidade. Um pico está localizado no comprimento de onda\(λ\), que é o comprimento de onda do feixe incidente. O outro pico está localizado em algum outro comprimento de onda,\(λ'\). Os dois picos são separados por\(Δλ\), o que depende do ângulo\(θ\) de dispersão do feixe de saída (na direção da observação). A separação\(Δλ\) é chamada de mudança de Compton.
Turno de Compton
Conforme dado por Compton, a explicação da mudança de Compton é que, no material alvo, grafite, elétrons de valência estão frouxamente ligados aos átomos e se comportam como elétrons livres. Compton presumiu que a radiação de raios-X incidente é um fluxo de fótons. Um fóton entrante nesse fluxo colide com um elétron de valência no alvo de grafite. Durante essa colisão, o fóton entrante transfere parte de sua energia e momento para o elétron alvo e sai de cena como um fóton disperso. Esse modelo explica em termos qualitativos por que a radiação dispersa tem um comprimento de onda maior do que a radiação incidente. Simplificando, um fóton que perdeu parte de sua energia surge como um fóton com uma frequência mais baixa, ou equivalentemente, com um comprimento de onda maior. Para mostrar que seu modelo estava correto, Compton o usou para derivar a expressão para o turno de Compton. Em sua derivação, ele assumiu que tanto o fóton quanto o elétron são partículas relativistas e que a colisão obedece a dois princípios de bom senso:
- a conservação do momento linear e
- a conservação da energia relativista total.
Na derivação a seguir do deslocamento de Compton,\(E_f\) e\(\vec{p}_f\) denote a energia e o momento, respectivamente, de um fóton incidente com frequência\(f\). O fóton colide com um elétron relativístico em repouso, o que significa que imediatamente antes da colisão, a energia do elétron é inteiramente sua energia de massa restante,\(m_0c^2\). Imediatamente após a colisão, o elétron tem energia\(E\) e momento\(\vec{p}\), os quais satisfazem a Equação\ ref {6.19}. Imediatamente após a colisão, o fóton de saída tem energia\(\vec{\tilde{E}}_f\)\(\vec{\tilde{p}}_f\), momento e frequência\(f'\). A direção do fóton incidente é horizontal da esquerda para a direita, e a direção do fóton de saída está no ângulo\(θ\), conforme ilustrado na Figura\(\PageIndex{1}\). O ângulo de dispersão\(θ\) é o ângulo entre os vetores de momento\(\vec{p}_f\) e\(\vec{\tilde{p}}_f\), e podemos escrever seu produto escalar:
\[\vec{p} \cdot \vec{\tilde{p}}_f = p_f\vec{p}_f \cos \, \theta. \label{6.23} \]
Seguindo o argumento de Compton, assumimos que a colisão do fóton e do elétron formam um sistema isolado. Essa suposição é válida para elétrons fracamente ligados que, até uma boa aproximação, podem ser tratados como partículas livres. Nossa primeira equação é a conservação de energia para o sistema fóton-elétron:
\[E_f + m_0c^2 = \tilde{E}_f + E. \label{6.24} \]
O lado esquerdo dessa equação é a energia do sistema no instante imediatamente anterior à colisão, e o lado direito da equação é a energia do sistema no instante imediatamente após a colisão. Nossa segunda equação é a conservação do momento linear para o sistema fóton-elétron, onde o elétron está em repouso no instante imediatamente anterior à colisão:
\[\vec{p}_f = \vec{\tilde{p}}_f + \vec{p}. \label{6.25} \]
O lado esquerdo dessa equação é o momento do sistema logo antes da colisão, e o lado direito da equação é o momento do sistema logo após a colisão. Toda a física da dispersão de Compton está contida nessas três equações anteriores — a parte restante é álgebra. Neste ponto, poderíamos pular para a fórmula final da mudança de Compton, mas é benéfico destacar as principais etapas algébricas que levam à fórmula de Compton, que apresentamos aqui da seguinte forma.
Começamos reorganizando os termos na Equação\ ref {6.24} e colocando-os ao quadrado:
\[[(E_f - \tilde{E}_f) + m_0c^2]^2 = E^2. \nonumber \]
Na próxima etapa, substituímos Equation\ ref {6.19} por\(E^2\), simplificamos e dividimos os dois lados por\(c^2\) para obter
\[(E_f / c - \tilde{E}_f / c)^2 + 2m_0c (E_f / c - \tilde{E}_f / c) = p^2. \nonumber \]
Agora podemos usar a Equação\ ref {6.21} para expressar essa forma da equação de energia em termos de momentos. O resultado é
\[(p_f - \tilde{p}_f)^2 + 2m_0 c(p_f - \tilde{p}_f) = p^2. \label{6.26} \]
Para eliminar\(p^2\), recorremos à equação de momento Equação\ ref {6.25}, reorganizamos seus termos e colocamos ao quadrado para obter
\[ \begin{align*} (\vec{p}_f - \vec{\tilde{p}}_f)^2 &= p^2 \\[4pt] &= p_f^2 + \tilde{p}_f^2 - 2p_f \tilde{p}_f \, \cos \, \theta. \end{align*} \nonumber \]
O produto dos vetores de momento é dado pela Equação\ ref {6.23}. Quando substituímos esse resultado\(p^2\) na Equação\ ref {6.26}, obtemos a equação de energia que contém o ângulo de dispersão θ:
\[(p_f - \tilde{p}_f)^2 + 2m_0c(p_f - \tilde{p}_f) = p_f^2 + \tilde{p}_f^2 - 2p_f \tilde{p}_f \, \cos \, \theta. \nonumber \]
Com mais álgebra, esse resultado pode ser simplificado para
\[\dfrac{1}{\tilde{p}_f} - \dfrac{1}{p_f} = \dfrac{1}{m_0c}(1 - \cos \, \theta). \label{6.27} \]
Agora, recupere a Equação\ ref {6.21} e escreva:\(1/\tilde{p}_f = \lambda' /h\)\(1/p_f = \lambda /h\) e. Quando essas relações são substituídas na Equação\ ref {6.27}, obtemos a relação para a mudança de Compton:
\[\lambda' - \lambda = \dfrac{h}{m_0c}(1 - \cos \, \theta). \label{6.28} \]
O fator\(h/m_0c\) é chamado de comprimento de onda Compton do elétron:
\[\lambda_c = \dfrac{h}{m_0c} = 0.00243 \, nm = 2.43 \, pm. \label{6.29} \]
Denotando a mudança como\(\Delta \lambda = \lambda' - \lambda\), o resultado final pode ser reescrito como
\[\Delta \lambda = \lambda_c (1 - \cos \, \theta). \label{6.30} \]
Esta fórmula para a mudança de Compton descreve muito bem os resultados experimentais mostrados na Figura\(\PageIndex{2}\). Os dados de dispersão medidos para molibdênio, grafite, calcita e muitos outros materiais alvo estão de acordo com esse resultado teórico. O pico não deslocado mostrado na Figura\(\PageIndex{1}\) é devido a colisões de fótons com elétrons internos fortemente ligados no material alvo. Os fótons que colidem com os elétrons internos dos átomos alvo, na verdade, colidem com o átomo inteiro. Nesse caso extremo, a massa restante na Equação\ ref {6.29} deve ser alterada para a massa restante do átomo. Esse tipo de mudança é quatro ordens de magnitude menor do que a mudança causada por colisões com elétrons e é tão pequena que pode ser negligenciada.
O espalhamento Compton é um exemplo de dispersão inelástica, em que a radiação dispersa tem um comprimento de onda maior do que o comprimento de onda da radiação incidente. No uso atual, o termo “dispersão de Compton” é usado para a dispersão inelástica de fótons por partículas livres e carregadas. No espalhamento de Compton, tratar fótons como partículas com momentos que podem ser transferidos para partículas carregadas fornece a base teórica para explicar as mudanças de comprimento de onda medidas em experimentos; essa é a evidência de que a radiação consiste em fótons.
Um raio-X incidente às 19h é incidente em um alvo de calcita. Encontre o comprimento de onda do raio X espalhado em um ângulo de 30°30°. Qual é a maior mudança que se pode esperar neste experimento?
Estratégia
Para encontrar o comprimento de onda do raio-X disperso, primeiro precisamos encontrar o desvio de Compton para o ângulo de dispersão dado,\(\theta = 30°\). Usamos a Equação\ ref {6.30}. Em seguida, adicionamos essa mudança ao comprimento de onda incidente para obter o comprimento de onda disperso. O maior deslocamento de Compton ocorre no ângulo\(\theta\) quando\(1 - \cos \, \theta\) tem o maior valor, que é para o ângulo\(\theta = 180°\).
Solução
A mudança em\(\theta = 30°\) é
\[\begin{align*} \Delta \lambda &= \lambda_c (1 - \cos \, 30°) \\[4pt] &= 0.134 \lambda_c \\[4pt] &= (0.134)(2.43) \, pm \\[4pt] &= 0.32 \end{align*} \nonumber \]
Isso fornece o comprimento de onda disperso:
\[\begin{align*} \lambda' &= \lambda + \Delta \lambda \\[4pt] &= (71 + 0.325) \, pm \\[4pt] &= 71.325 \,pm. \end{align*} \nonumber \]
A maior mudança é
\[\begin{align*} (\Delta \lambda )_{max} &= \lambda_c(1 − \cos \, 180°) \\[4pt] &= 2(2.43 \, pm) \\[4pt] &= 4.86 \, pm. \end{align*} \nonumber \]
Significância
A maior mudança no comprimento de onda é detectada pela radiação retroespalhada; no entanto, a maioria dos fótons do feixe incidente passa pelo alvo e apenas uma pequena fração dos fótons é retroespalhada (normalmente, menos de 5%). Portanto, essas medições exigem detectores altamente sensíveis.
Um raio-X incidente às 19h é incidente em um alvo de calcita. Encontre o comprimento de onda do raio X espalhado em um ângulo de 60°. Qual é a menor mudança que se pode esperar neste experimento?
- Resposta
-
\((\Delta \lambda)_{min} = 0 \, m\)em um ângulo de 0°;\(71.0 \, pm + 0.5 \lambda_c = 72.215 \, pm\)


