2.5: Lentes finas

Last updated
Save as PDF

Page ID: 183235

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Use diagramas de raios para localizar e descrever a imagem formada por uma lente
Use a equação de lente fina para descrever e localizar a imagem formada por uma lente

As lentes são encontradas em uma grande variedade de instrumentos ópticos, desde uma simples lupa até a lente de zoom de uma câmera e o próprio olho. Nesta seção, usamos a lei de Snell para explorar as propriedades das lentes e como elas formam imagens.

A palavra “lente” deriva da palavra latina para feijão de lentilha, cujo formato é semelhante a uma lente convexa. No entanto, nem todas as lentes têm o mesmo formato. A figura\(\PageIndex{1}\) mostra uma variedade de formas diferentes de lentes. O vocabulário usado para descrever lentes é o mesmo usado para espelhos esféricos: O eixo de simetria de uma lente é chamado de eixo óptico, onde esse eixo cruza a superfície da lente é chamado de vértice da lente, e assim por diante.

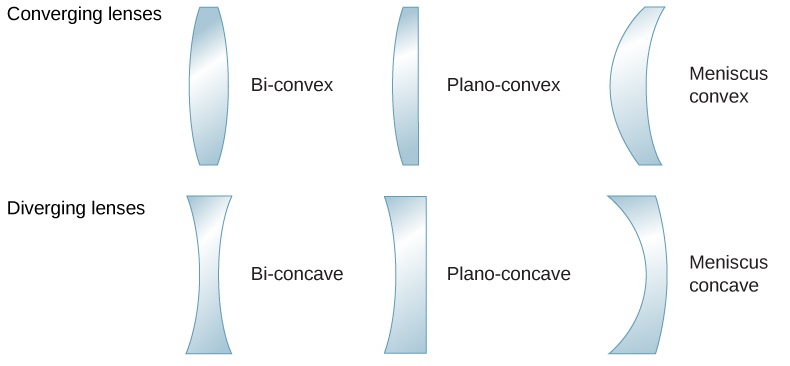
A figura mostra três lentes convergentes e três lentes divergentes. As lentes convergentes são: biconvexas, com duas superfícies convexas, plano-convexas, com uma superfície convexa e uma vez plana e menisco convexo, com uma superfície convexa e uma côncava, a convexa com um raio de curvatura menor. As lentes divergentes são: bicôncavas, com duas superfícies côncavas, plano-côncava, com uma superfície côncava e outra plana e menisco côncavo, com uma superfície côncava e outra convexa, com a côncava com um raio de curvatura menor. — Figura\(\PageIndex{1}\): Vários tipos de lentes: Observe que uma lente convergente tem uma “cintura” mais grossa, enquanto uma lente divergente tem uma cintura mais fina.

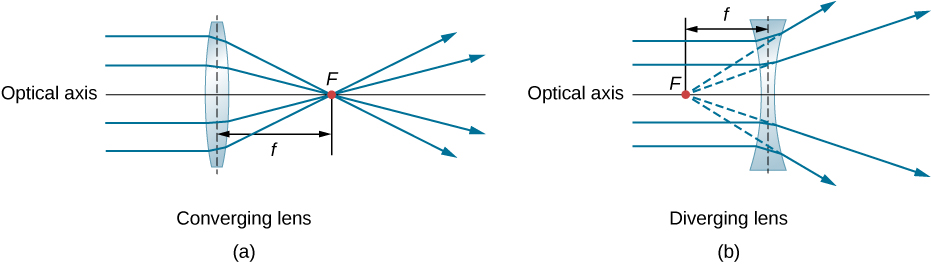
Uma lente convexa ou convergente é moldada de forma que todos os raios de luz que entram nela paralelamente ao seu eixo óptico se cruzem (ou focalizem) em um único ponto no eixo óptico no lado oposto da lente, conforme mostrado na Figura\(\PageIndex{1a}\). Da mesma forma, uma lente côncava ou divergente tem o formato de forma que todos os raios que entram nela paralelamente ao seu eixo óptico diverjam, conforme mostrado na parte (b). Para entender com mais precisão como uma lente manipula a luz, observe atentamente o raio superior que passa pela lente convergente na parte (a). Como o índice de refração da lente é maior que o do ar, a lei de Snell nos diz que o raio é curvado em direção à perpendicular à interface ao entrar na lente. Da mesma forma, quando o raio sai da lente, ele é curvado para longe da perpendicular. O mesmo raciocínio se aplica às lentes divergentes, conforme mostrado na Figura \(\PageIndex{1b}\). O efeito geral é que os raios de luz são curvados em direção ao eixo óptico de uma lente convergente e afastados do eixo óptico para lentes divergentes. Para uma lente convergente, o ponto em que os raios se cruzam é o ponto focal F da lente. Para uma lente divergente, o ponto do qual os raios parecem se originar é o ponto focal (virtual). A distância do centro da lente até seu ponto focal é a distância focal f da lente.

A Figura a mostra raios paralelos ao eixo óptico atingindo uma lente biconvexa e convergindo do outro lado no ponto F. A Figura b mostra raios paralelos ao eixo óptico atingindo uma lente bicôncava e divergindo no outro lado. Os raios divergentes são estendidos na parte traseira e parecem se originar do ponto F na frente da lente. Em ambas as figuras, a distância do centro da lente até o ponto F é identificada como f. — Figura\(\PageIndex{2}\): Os raios de luz que entram (a) em uma lente convergente e (b) em uma lente divergente, paralelamente ao seu eixo, convergem em seu ponto focal F. A distância do centro da lente até o ponto focal é a distância focal da lente f. Observe que os raios de luz são curvados ao entrar e sair do lente, com o efeito geral de dobrar os raios em direção ao eixo óptico.

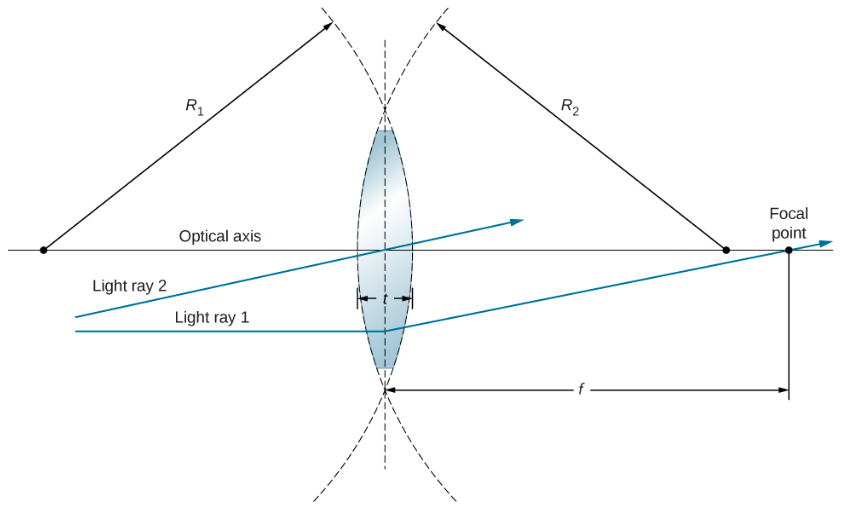
Uma lente é considerada fina se sua espessura t for muito menor que os raios de curvatura de ambas as superfícies, conforme mostrado na Figura\(\PageIndex{3}\). Nesse caso, pode-se considerar que os raios se curvam uma vez no centro da lente. Para o caso desenhado na figura, o raio de luz 1 é paralelo ao eixo óptico, então o raio de saída é dobrado uma vez no centro da lente e passa pelo ponto focal. Outra característica importante das lentes finas é que os raios de luz que passam pelo centro da lente são inalterados, conforme mostrado pelo raio de luz 2.

A figura mostra a seção transversal de uma lente biconvexa. Os raios de curvatura das superfícies direita e esquerda são R1 e R2, respectivamente. A espessura da lente é t. O raio de luz 1 entra na lente, se desvia e passa pelo ponto focal. O raio de luz 2 passa pelo centro da lente sem se desviar. — Figura\(\PageIndex{3}\): Na aproximação de lentes finas, a espessura t da lente é muito, muito menor do que os raios R ₁ e R ₂ de curvatura das superfícies da lente. Considera-se que os raios de luz se curvam no centro da lente, como o raio de luz 1. O raio de luz 2 passa pelo centro da lente e é inalterado na aproximação da lente fina.

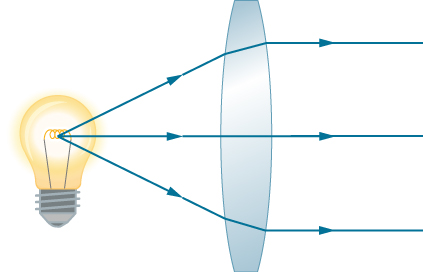
Conforme observado na discussão inicial da lei de Snell, os caminhos dos raios de luz são exatamente reversíveis. Isso significa que a direção das setas pode ser invertida para todos os raios na Figura \(\PageIndex{2}\). Por exemplo, se uma fonte de luz pontual for colocada no ponto focal de uma lente convexa, conforme mostrado na Figura \(\PageIndex{4}\), raios de luz paralelos emergem do outro lado.

A figura mostra os raios de uma lâmpada entrando em uma lente biconvexa e emergindo do outro lado como raios paralelos. — Figura\(\PageIndex{4}\) em lentes convergentes e divergentes. Essa técnica é usada em faróis e às vezes em semáforos para produzir um feixe de luz direcional de uma fonte que emite luz em todas as direções.

Ray Tracing e lentes finas

O traçado de raios é a técnica de determinar ou seguir (traçar) os caminhos percorridos pelos raios de luz. O traçado de raios para lentes finas é muito semelhante à técnica que usamos com espelhos esféricos. Quanto aos espelhos, o traçado de raios pode descrever com precisão a operação de uma lente. As regras para o traçado de raios para lentes finas são semelhantes às dos espelhos esféricos:

Um raio que entra em uma lente convergente paralela ao eixo óptico passa pelo ponto focal do outro lado da lente (raio 1 na parte (a) da Figura\(\PageIndex{4}\)). Um raio que entra em uma lente divergente paralela ao eixo óptico sai ao longo da linha que passa pelo ponto focal no mesmo lado da lente (raio 1 na parte (b) da figura).
Um raio que passa pelo centro de uma lente convergente ou divergente não é desviado (raio 2 nas partes (a) e (b)).
Para uma lente convergente, um raio que passa pelo ponto focal sai da lente paralelamente ao eixo óptico (raio 3 em parte (a)). Para uma lente divergente, um raio que se aproxima ao longo da linha que passa pelo ponto focal no lado oposto sai da lente paralelamente ao eixo (raio 3 em parte (b)).

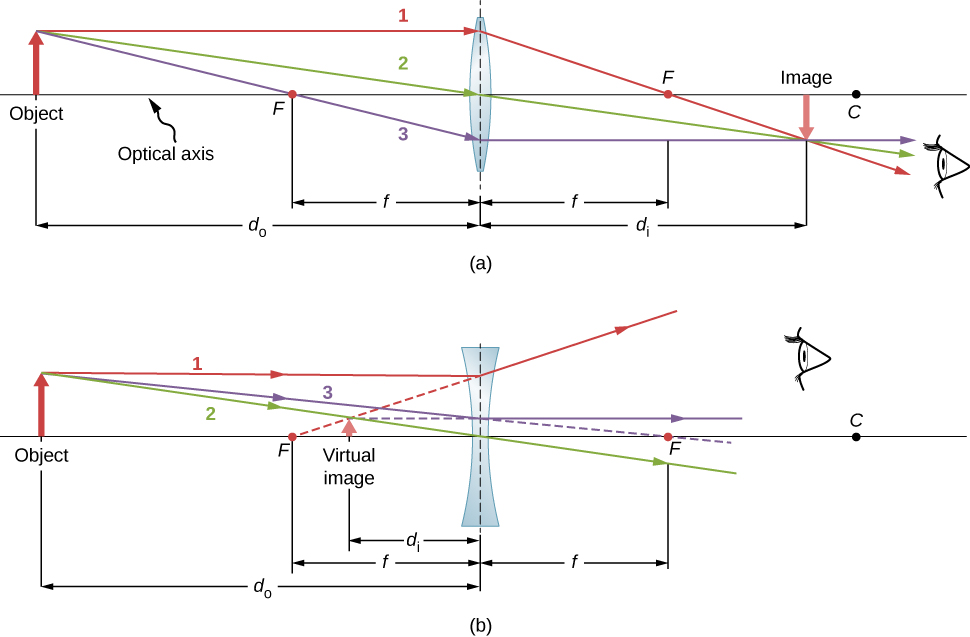
A Figura a mostra uma lente biconvexa com pontos focais em ambos os lados. Um objeto é colocado em seu eixo óptico. Três raios se originam da parte superior desse objeto e entram na lente. O raio 1 é paralelo ao eixo óptico. O raio 2 atinge o centro da lente. O raio 3 cruza o ponto focal antes de entrar na lente. Os raios convergem do outro lado para formar uma imagem. O raio 1 cruza o ponto focal e o raio 3 agora está paralelo ao eixo. A Figura b mostra uma lente bi-côncava com pontos focais em ambos os lados. Um objeto é colocado em seu eixo óptico. Três raios se originam da parte superior desse objeto e entram na lente. O raio 1 é paralelo ao eixo, o raio 2 atinge o centro da lente e o raio 3, se estendido em linha reta, cruzaria o ponto focal do outro lado da lente. Todos os três raios divergem do outro lado da lente. O raio 3 agora está paralelo ao eixo e a extensão traseira do raio 1 cruza o ponto focal na frente da lente. As extensões traseiras dos três raios convergem para formar uma imagem virtual, que é muito menor que o objeto, na frente da lente. — Figura\(\PageIndex{5}\): As lentes finas têm as mesmas distâncias focais em ambos os lados. (a) Raios de luz paralelos que entram em uma lente convergente pela direita se cruzam em seu ponto focal à esquerda. (b) Os raios de luz paralelos que entram em uma lente divergente pela direita parecem vir do ponto focal à direita.

As lentes finas funcionam muito bem com luz monocromática (ou seja, luz de um único comprimento de onda). No entanto, para luz que contém vários comprimentos de onda (por exemplo, luz branca), as lentes funcionam menos bem. O problema é que, como aprendemos no capítulo anterior, o índice de refração de um material depende do comprimento de onda da luz. Esse fenômeno é responsável por muitos efeitos coloridos, como arco-íris. Infelizmente, esse fenômeno também leva a aberrações nas imagens formadas por lentes. Em particular, como a distância focal da lente depende do índice de refração, ela também depende do comprimento de onda da luz incidente. Isso significa que a luz de diferentes comprimentos de onda se concentrará em pontos diferentes, resultando nas chamadas “aberrações cromáticas”. Em particular, as bordas de uma imagem de um objeto branco ficarão coloridas e desfocadas. Lentes especiais chamadas duplas são capazes de corrigir aberrações cromáticas. Um gibão é formado pela colagem de uma lente convergente e uma lente divergente. A lente dupla combinada produz aberrações cromáticas significativamente reduzidas.

Formação de imagem por lentes finas

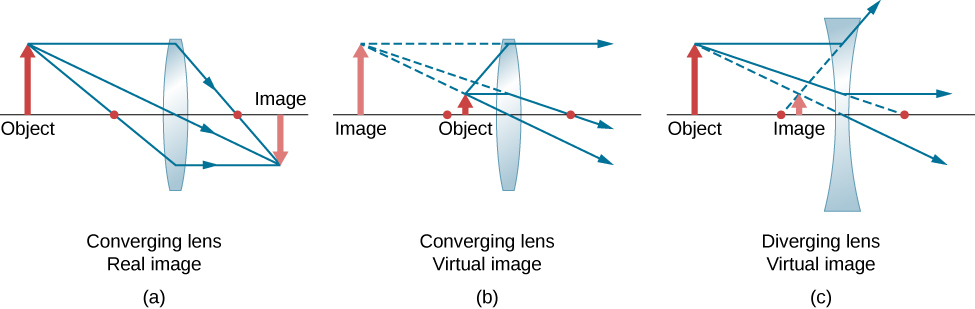
Usamos o traçado de raios para investigar diferentes tipos de imagens que podem ser criadas por uma lente. Em algumas circunstâncias, uma lente forma uma imagem real, como quando um projetor de filme projeta uma imagem em uma tela. Em outros casos, a imagem é virtual, que não pode ser projetada em uma tela. Onde, por exemplo, está a imagem formada pelos óculos? Usamos o traçado de raios para lentes finas para ilustrar como elas formam imagens e, em seguida, desenvolvemos equações para analisar quantitativamente as propriedades das lentes finas.

Considere um objeto a alguma distância de uma lente convergente, conforme mostrado na Figura\(\PageIndex{6}\). Para encontrar a localização e o tamanho da imagem, traçamos os caminhos dos raios de luz selecionados originados de um ponto do objeto, neste caso, a ponta da seta. A figura mostra três raios de muitos raios que emanam da ponta da flecha. Esses três raios podem ser rastreados usando as regras de rastreamento de raios fornecidas acima.

O raio 1 entra na lente paralelamente ao eixo óptico e passa pelo ponto focal no lado oposto (regra 1).
O raio 2 passa pelo centro da lente e não se desvia (regra 2).
O raio 3 passa pelo ponto focal até a lente e sai da lente paralelamente ao eixo óptico (regra 3).

Os três raios se cruzam em um único ponto no lado oposto da lente. Assim, a imagem da ponta da flecha está localizada nesse ponto. Todos os raios que saem da ponta da seta e entram na lente são refratados e se cruzam no ponto mostrado.

Depois de localizar a imagem da ponta da seta, precisamos de outro ponto da imagem para orientar toda a imagem da seta. Optamos por localizar a base da imagem da seta, que está no eixo óptico. Conforme explicado na seção sobre espelhos esféricos, a base estará no eixo óptico logo acima da imagem da ponta da seta (devido à simetria superior inferior da lente). Assim, a imagem abrange o eixo óptico até a altura (negativa) mostrada. Raios de outro ponto na seta, como o meio da seta, se cruzam em outro ponto comum, preenchendo assim o resto da imagem.

Embora três raios sejam traçados nessa figura, apenas dois são necessários para localizar um ponto da imagem. É melhor traçar raios para os quais existem regras simples de rastreamento de raios.

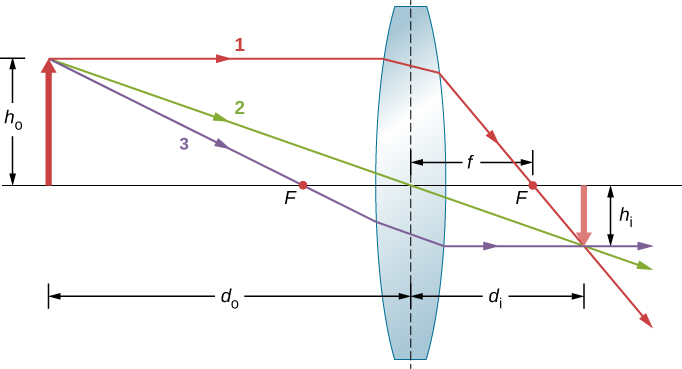
A figura mostra a seção transversal de uma lente biconvexa. Três raios se originam da parte superior de um objeto e entram na lente. O raio 1 é paralelo ao eixo óptico. O raio 2 cruza o centro da lente. O raio 3 cruza o ponto focal na frente da lente. Todos os raios convergem para o outro lado na parte superior de uma imagem invertida. O raio 1 cruza o ponto focal atrás da lente. O raio 2 é inalterado. O raio 3 fica paralelo ao eixo óptico. A distância do objeto e as distâncias da imagem são d subscrito o e d subscrito I, respectivamente. As alturas do objeto e da imagem são h subscrito o e h subscrito I, respectivamente. A distância focal é f. — Figura\(\PageIndex{6}\): O traçado de raios é usado para localizar a imagem formada por uma lente. Raios originados do mesmo ponto do objeto são traçados — cada um dos três raios escolhidos segue uma das regras de traçado de raios, para que seus caminhos sejam fáceis de determinar. A imagem está localizada no ponto em que os raios se cruzam. Nesse caso, uma imagem real, que pode ser projetada em uma tela, é formada.

Várias distâncias importantes aparecem na figura. Quanto a um espelho, definimos dodô como sendo a distância do objeto ou a distância de um objeto do centro de uma lente. A distância da imagem d _i é definida como a distância da imagem do centro de uma lente. A altura do objeto e a altura da imagem são indicadas por h _o e h _i, respectivamente. As imagens que aparecem na vertical em relação ao objeto têm alturas positivas e as que estão invertidas têm alturas negativas. Usando as regras do traçado de raios e fazendo um desenho em escala com papel e lápis, como na Figura \(\PageIndex{6}\), podemos descrever com precisão a localização e o tamanho de uma imagem. Mas o benefício real do traçado de raios está em visualizar como as imagens são formadas em uma variedade de situações.

Raios paralelos oblíquos e plano focal

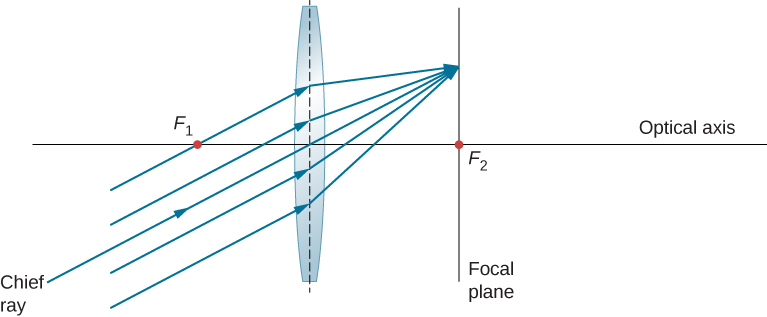
Vimos que os raios paralelos ao eixo óptico são direcionados para o ponto focal de uma lente convergente. No caso de lentes divergentes, elas saem em uma direção tal que parecem estar vindo do ponto focal no lado oposto da lente (ou seja, o lado do qual os raios paralelos entram na lente). O que acontece com os raios paralelos que não são paralelos ao eixo óptico (Figura \(\PageIndex{7}\))? No caso de uma lente convergente, esses raios não convergem no ponto focal. Em vez disso, eles se juntam em outro ponto do plano chamado plano focal. O plano focal contém o ponto focal e é perpendicular ao eixo óptico. Conforme mostrado na figura, os raios paralelos focam onde o raio que passa pelo centro da lente cruza o plano focal.

A figura mostra raios que são paralelos entre si, mas não ao eixo óptico, entrando em uma lente biconvexa e convergindo do outro lado em um ponto no plano focal. A seção transversal do plano focal é mostrada como uma linha perpendicular ao eixo óptico e a cruza no ponto focal. — Figura\(\PageIndex{7}\): Os raios oblíquos paralelos se concentram em um ponto em um plano focal.

Equação de lente fina

O traçado de raios nos permite obter uma imagem qualitativa da formação da imagem. Para obter informações numéricas, derivamos um par de equações de uma análise geométrica do traçado de raios para lentes finas. Essas equações, chamadas de equação de lente fina e equação do fabricante de lentes, nos permitem analisar quantitativamente lentes finas.

Considere a lente biconvexa espessa mostrada na Figura \(\PageIndex{8}\). O índice de refração do meio circundante é n ₁ (se a lente estiver no ar, então\(n_1=1.00\)) e o da lente é\(n_2\). Os raios das curvaturas dos dois lados são\(R_1\)\(R_2\) e. Queremos encontrar uma relação entre a distância do objeto\(d_o\), a distância\(d_i\) da imagem e os parâmetros da lente.

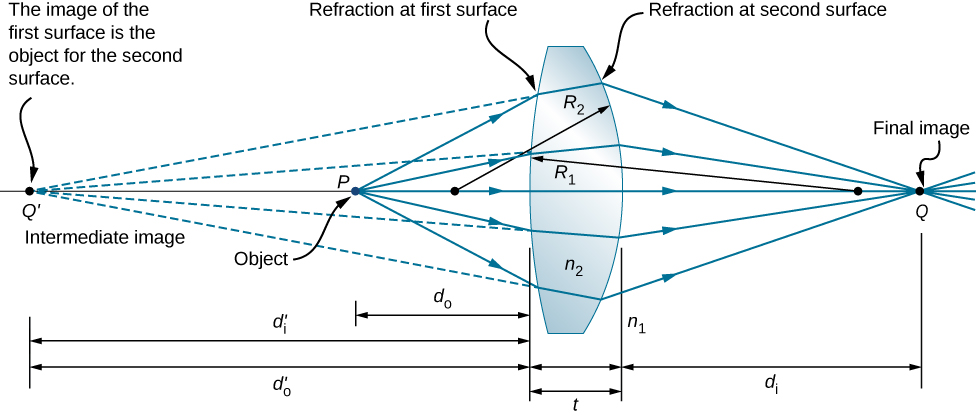
A figura mostra uma lente biconvexa com espessura t e raios de curvatura das superfícies frontal e traseira R1 e R2, respectivamente. O índice de refração do ar e da lente é n1 e n2, respectivamente. Os raios de um objeto no ponto P no eixo óptico na frente da lente atingem a primeira superfície e são refratados dentro da lente. As extensões posteriores dos raios refratados convergem no ponto Q primo para formar uma imagem intermediária. Q prime está na frente da lente, mais longe dela do que P. Os raios dentro da lente refratam ainda mais à medida que emergem da segunda superfície. Eles convergem no ponto Q atrás da lente para formar a imagem final. As distâncias da lente até o objeto, a imagem intermediária e a imagem final são d0, d0 prime e di, respectivamente. d0 prime também é igual a di prime. — Figura\(\PageIndex{8}\) para derivar a equação do fabricante da lente. Aqui,\(t\) é a espessura da lente, n ₁ é o índice de refração do meio externo e\(n_2\) é o índice de refração da lente. Tomamos o limite de\(t→0\) para obter a fórmula para uma lente fina.

Para derivar a equação de lente fina, consideramos a imagem formada pela primeira superfície refratária (ou seja, superfície esquerda) e, em seguida, usamos essa imagem como objeto para a segunda superfície refratária. Na figura, a imagem da primeira superfície refratária é\(Q′\) formada pela extensão dos raios de dentro da lente para trás (esses raios resultam da refração na primeira superfície). Isso é mostrado pelas linhas tracejadas na figura. Observe que essa imagem é virtual porque nenhum raio realmente passa pelo ponto Q′. Para encontrar a distância da imagem\(d′_i\) correspondente à imagem Q', usamos a Equação 2.4.9. Nesse caso, a distância do objeto é\(d_o\), a distância da imagem é d′idi′e o raio de curvatura é\(R_1\). Inseri-los na relação derivada anteriormente para refração em superfícies curvas fornece

\ [\ dfrac {n_1} {d_o} +\ dfrac {n_2} {d′_i} =\ dfrac {n_2−n_1} {R_1}. \ label {51}\]

A imagem é virtual e está do mesmo lado do objeto, então d _i ′<0 e d _o >0. A primeira superfície é convexa em direção ao objeto, então\(R_1>0\).

Para encontrar a distância do objeto\(Q\) formado pela refração da segunda interface, observe que o papel dos índices de refração n ₁ e n ₂ é trocado na Equação 2.4.9. Na Figura\(\PageIndex{8}\), os raios se originam no meio com índice\(n_2\), enquanto na Figura 2.4.3, os raios se originam no meio com índice \(n_1\). Assim, devemos trocar n ₁ e n ₂ na Equação 2.4.9. Além disso, consultando novamente a Figura\(\PageIndex{8}\), vemos que a distância do objeto é\(d′_o\) e a distância da imagem é \(d_i\). O raio de curvatura é R ₂. A inserção dessas quantidades na Equação 2.4.9 dá

\ [\ dfrac {n_2} {d′_o} +\ dfrac {n_1} {d_i} =\ dfrac {n_1−n_2} {R_2}. \ label {eq51}\]

A imagem é real e está no lado oposto do objeto, então \(d_i>0\)\(d_o′>0\) e. A segunda superfície é convexa longe do objeto, então\(R_2<0\). A equação\ ref {eq51} pode ser simplificada observando que

\[d′_o=|d′_i|+t, \nonumber \]

onde tomamos o valor absoluto porque\(d′_i\) é um número negativo, enquanto ambos\(d′_o\) e\(t\) são positivos. Podemos dispensar o valor absoluto se negarmos\(d′_i\), o que dá

\[ d′_o=−d′_i+td. \nonumber \]

Inserindo isso na Equação\ ref {eq51} dá

\ [\ dfrac {n_2} {−d′_i+t} +\ dfrac {n_1} {d_i} =\ dfrac {n_1−n_2} {R_2}. \ label {eq52}\]

A soma das equações\ ref {eq51} e\ ref {eq52} dá

\ [\ dfrac {n_1} {d_o} +\ dfrac {n_1} {d_i} +\ dfrac {n_2} {d′_i} +\ dfrac {n_2} {−d′_i+t} = (n_2−n_1) \ left (\ dfrac {1} {R_1} −\ dfrac c {1} {R_2}\ direita). \ label {eq54}\]

Na aproximação de lentes finas, assumimos que a lente é muito fina em comparação com a primeira distância da imagem, ou\(t \ll d′_i\) (ou, equivalentemente,\(t \ll R_1\) e\(t \ll R_2\)). Nesse caso, o terceiro e o quarto termos no lado esquerdo da Equação\ ref {eq54} cancelam, deixando-nos com

\ [\ dfrac {n_1} {d_o} +\ dfrac {n_1} {d_i} = (n_2−n_1) \ left (\ dfrac {1} {R_1} −\ dfrac {1} {R_2}\ direita). \ nonumber\]

Dividir por nos\(n_1\) dá finalmente

\ [\ dfrac {1} {d_o} +\ dfrac {1} {d_i} =\ left (\ dfrac {n_2} {n_1} −1 \ direita)\ left (\ dfrac {1} {R_1} −\ dfrac {1} {R_2}\ direita). \ label {eq58}\]

O lado esquerdo se parece suspeitosamente com a equação do espelho que derivamos acima para espelhos esféricos. Como feito para espelhos esféricos, podemos usar traçado de raios e geometria para mostrar que, para uma lente fina,

\ [ \ underbrace {\ dfrac {1} {d_o} +\ dfrac {1} {d_i} =\ dfrac {1} {f}} _ { \ text {equação de lente fina}}\ label {equação de lente fina}\]

onde\(f\) está a distância focal da lente fina (essa derivação é deixada como um exercício). Essa é a equação da lente fina. A distância focal de uma lente fina é a mesma à esquerda e à direita da lente. A combinação das equações \ ref {equação de lente fina} e\ ref {eq58} dá

\ [\ underbrace {\ dfrac {1} {f} =\ left (\ dfrac {n_2} {n_1} −1\ right) \ left (\ dfrac {1} {R_1} −\ dfrac {1} {R_2}\ right)} _ {\ text { equação do fabricante de lentes}}\ label {lensmaker}\]

que é chamada de equação do fabricante de lentes. Isso mostra que a distância focal de uma lente fina depende apenas dos raios de curvatura e do índice de refração da lente e do meio circundante. Para uma lente no ar,\(n_1=1.0\) e, portanto\(n_2≡n\), a equação do fabricante da lente se reduz para

\ [\ dfrac {1} {f} = (n−1) \ left (\ dfrac {1} {R_1} −\ dfrac {1} {R_2}\ direita). \ nonumber\]

Convenções de sinalização para lentes

Para usar corretamente a equação de lente fina, as seguintes convenções de sinais devem ser obedecidas:

\(d_i\)é positivo se a imagem estiver no lado oposto ao objeto (ou seja, imagem real); caso contrário,\(d_i\) é negativo (ou seja, imagem virtual).
\(f\)é positivo para uma lente convergente e negativo para uma lente divergente.
\(R\)é positivo para uma superfície convexa em direção ao objeto e negativo para uma superfície côncava em direção ao objeto.

Ampliação

Usando um objeto de tamanho finito no eixo óptico e no traçado de raios, você pode mostrar que a ampliação\(m\) de uma imagem é

\[m \equiv \dfrac{h_i}{h_o}=−\dfrac{d_i}{d_o} \label{mag} \]

(onde as três linhas significam “é definido como”). Essa é exatamente a mesma equação que obtivemos para espelhos (veja a Equação 2.3.15). Se\(m>0\) sim, então a imagem tem a mesma orientação vertical do objeto (chamada de imagem “vertical”). Se m<0 , a imagem tem a orientação vertical oposta à do objeto (chamada de imagem “invertida”).

Usando a equação de lente fina

A equação da lente fina e a equação do fabricante da lente são amplamente aplicáveis a situações que envolvem lentes finas. Exploramos muitas características da formação de imagens nos exemplos a seguir.

Considere uma lente convergente fina. Onde a imagem se forma e que tipo de imagem é formada quando o objeto se aproxima da lente do infinito? Isso pode ser visto usando a equação de lente fina para uma determinada distância focal para traçar a distância da imagem em função da distância do objeto. Em outras palavras, traçamos

\[d_i=\left(\dfrac{1}{f}−\dfrac{1}{d_o}\right)^{−1} \nonumber \]

para um determinado valor de\(f\). Para\(f=1\,cm\), o resultado é mostrado na Figura\(\PageIndex{9a}\).

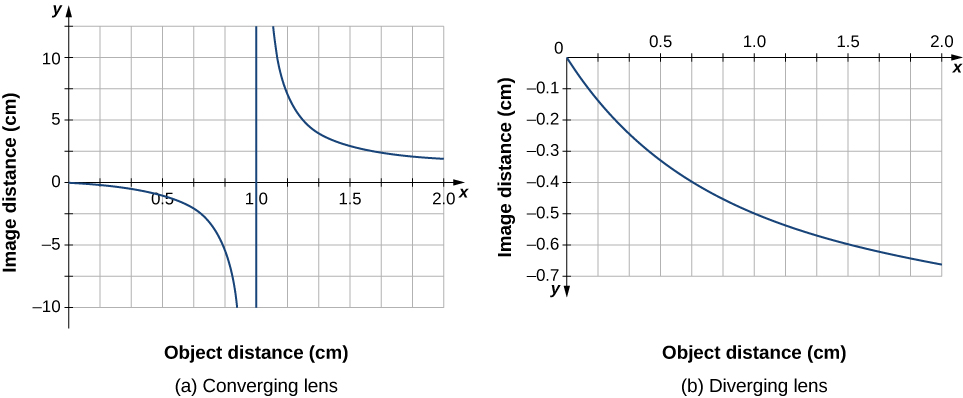
A Figura a mostra o gráfico de y igual a x sobre x - 1. A Figura b mostra o gráfico de y igual a x em −x-1. Em ambos os gráficos, o eixo y é rotulado como distância da imagem e o eixo x é rotulado como distância do objeto. — Figura\(\PageIndex{9}\): (a) Distância da imagem para uma lente convergente fina com f = 1,0 cm em função da distância do objeto. (b) A mesma coisa, mas para uma lente divergente com f = −1,0 cm.

Um objeto muito mais distante do que a distância focal f da lente deve produzir uma imagem próxima ao plano focal, porque o segundo termo no lado direito da equação acima se torna insignificante em comparação com o primeiro termo, então temos\(d_i≈f\). Isso pode ser visto no gráfico da parte (a) da figura, que mostra que a distância da imagem se aproxima assintoticamente da distância focal de 1 cm para maiores distâncias de objetos. Conforme o objeto se aproxima do plano focal, a distância da imagem diverge para o infinito positivo. Isso é esperado porque um objeto no plano focal produz raios paralelos que formam uma imagem no infinito (ou seja, muito longe da lente). Quando o objeto está mais distante do que a distância focal da lente, a distância da imagem é positiva, então a imagem é real, no lado oposto da lente do objeto, e invertida (porque \(m=−d_i/d_o\) via Equation\ ref {mag}). Quando o objeto está mais próximo do que a distância focal da lente, a distância da imagem se torna negativa, o que significa que a imagem é virtual, no mesmo lado da lente que o objeto e na vertical.

Para uma lente divergente fina de distância focal\(f =−1.0\, cm\), um gráfico semelhante da distância da imagem versus distância do objeto é mostrado na Figura\(\PageIndex{10b}\). Nesse caso, a distância da imagem é negativa para todas as distâncias positivas do objeto, o que significa que a imagem é virtual, no mesmo lado da lente do objeto e na vertical. Essas características também podem ser vistas por diagramas de traçado de raios (Figura\(\PageIndex{10}\)).

A Figura a mostra uma lente biconvexa, um objeto que está mais longe do que a distância focal e uma imagem invertida atrás da lente. A Figura b mostra uma lente biconvexa, um objeto que está mais próximo do que a distância focal e uma imagem vertical na frente da lente, mais distante do que o ponto focal. A Figura c mostra uma lente bicôncava, um objeto que está mais longe do que a distância focal e uma imagem vertical na frente da lente, entre a lente e o ponto focal. — Figura\(\PageIndex{10}\): Os pontos vermelhos mostram os pontos focais das lentes. (a) Uma imagem real invertida formada a partir de um objeto que está mais distante do que a distância focal de uma lente convergente. (b) Uma imagem virtual vertical formada a partir de um objeto que está mais próximo do que uma distância focal da lente. (c) Uma imagem virtual vertical formada a partir de um objeto que está mais distante do que uma distância focal de uma lente divergente.

Para ver um exemplo concreto de imagens verticais e invertidas, veja a Figura\(\PageIndex{11}\), que mostra imagens formadas por lentes convergentes quando o objeto (neste caso, o rosto da pessoa) é colocado a distâncias diferentes da lente. Na parte (a) da figura, o rosto da pessoa está a mais de uma distância focal da lente, então a imagem é invertida. Na parte (b), o rosto da pessoa está mais próximo do que uma distância focal da lente, então a imagem está na vertical.

A figura a mostra um homem segurando uma lente, com uma pequena imagem invertida de seu rosto visível nela. A Figura b mostra um homem segurando uma lente com uma imagem ampliada de seu olho visível nela. — Figura\(\PageIndex{11}\): (a) Quando uma lente convergente é mantida a mais de uma distância focal do rosto do homem, uma imagem invertida é formada. Observe que a imagem está em foco, mas o rosto não, porque a imagem está muito mais próxima da câmera tirando essa fotografia do que do rosto. (b) Uma imagem vertical do rosto do homem é produzida quando uma lente convergente é mantida a menos de uma distância focal de seu rosto. (crédito a: modificação da obra por “DaMongman” /Flickr; crédito b: modificação da obra de Casey Fleser)

Veja os exemplos a seguir para entender melhor como as lentes finas funcionam.

ESTRATÉGIA DE RESOLUÇÃO DE PROBLEMAS: LENTES

Etapa 1. Determine se o traçado de raios, a equação de lente fina ou ambos seriam úteis. Mesmo que o traçado de raios não seja usado, um esboço cuidadoso é sempre muito útil. Escreva símbolos e valores no esboço.
Etapa 2. Identifique o que precisa ser determinado no problema (identifique as incógnitas).
Etapa 3. Faça uma lista do que é dado ou pode ser deduzido do problema (identifique os conhecidos).
Etapa 4. Se o traçado de raios for necessário, use as regras de traçado de raios listadas no início desta seção.
Etapa 5. A maioria dos problemas quantitativos requer o uso da equação da lente fina e/ou da equação do fabricante da lente. Resolva-os para as incógnitas e insira as quantidades fornecidas ou use as duas juntas para encontrar duas incógnitas.
Etapa 7. Verifique se a resposta é razoável. Os sinais estão corretos? O esboço ou o traçado de raios são consistentes com o cálculo?

Exemplo\(\PageIndex{1}\): Usando a equação do fabricante de lentes

Encontre o raio de curvatura de uma lente bicôncava retificada simetricamente a partir de um vidro com índice de refração de 1,55 para que sua distância focal no ar seja de 20 cm (para uma lente bicôncava, ambas as superfícies têm o mesmo raio de curvatura).

Estratégia

Use a forma de lente fina da equação do fabricante da lente:

\ [\ dfrac {1} {f} =\ left (\ dfrac {n_2} {n_1} −1\ direita)\ left (\ dfrac {1} {R_1} −\ dfrac {1} {R_2}\ direita) \ nonumber\]

onde\(R_1<0\)\(R_2>0\) e. Como estamos fazendo uma lente bicôncava simétrica, temos\(|R_1|=|R_2|\).

Solução

Podemos determinar o raio\(R\) de curvatura de

\ [\ dfrac {1} {f} = \ left (\ dfrac {n_2} {n_1} −1\ direita)\ left (\ dfrac {−2} {R}\ direita). \ nonumber\]

Resolvendo\(R\) e inserindo\(f=−20\,cm\)\(n_2=1.55\), e \(n_1=1.00\) dá

\ [\ begin {align} R &=−2f\ left (\ dfrac {n_2} {n_1} −1\ right) \ nonumber\\ [4pt] &=−2 (−20\, cm) \ left (\ dfrac {1.55} {1.00} −1\ right)\ nonumber\\ [4pt] &= 22\, cm. \ nonumber\ end {align}\ nonumber\]

Exemplo\(\PageIndex{2}\): lente convergente e diferentes distâncias de objetos

Encontre a localização, orientação e ampliação da imagem para um objeto de 3,0 cm de altura em cada uma das seguintes posições na frente de uma lente convexa de distância focal de 10,0 cm. (a) \(d_o=50.0\,cm\), (b)\(d_o=5.00\,cm\) e (c)\ (d_o=20,0\, cm\).

Estratégia

Começamos com a equação de lente fina (Equação\ ref { equação de lente fina})

\[\dfrac{1}{d_i}+\dfrac{1}{d_o}=\dfrac{1}{f}. \nonumber \]

Resolva isso para a distância da imagem\(d_i\) e insira a distância e a distância focal do objeto fornecidas.

Solução

a. Para\(d_o=50\, cm\) e\(f=+10\, cm\), isso dá

\ [\ begin {align} d_i &= \ left (\ dfrac {1} {f} −\ dfrac {1} {d_o}\ direita) ^ {−1}\ nonumber\\ [4pt] &=\ left (\ dfrac {1} {10,0\, cm} −\ dfrac {1} {50,0 cm}\ direita) ^ {−−−1} \ nonumber\\ [4pt] &=12,5\, cm\ nonumber\ end {align} \ nonumber\]

A imagem é positiva, então a imagem é real, está no lado oposto da lente do objeto e está a 12,6 cm da lente. Para encontrar a ampliação e a orientação da imagem, use

\ [\ begin {align} m &=−\ dfrac {d_i} {d_o}\ nonumber\\ [4pt] &=−\ dfrac {12,5\, cm} {50,0\, cm}\ nonumber\\ [4pt] &=−0,250. \ nonumber\ end {align}\ nonumber\]

A ampliação negativa significa que a imagem está invertida. Desde então\(|m|<1\), a imagem é menor que o objeto. O tamanho da imagem é dado por

\ [\ begin {align} |h_i| &=|m|h_o \ nonumber\\ [4pt] & =( 0,250) (3,0\, cm)\ nonumber\\ [4pt] &=0,75\, cm\ nonumber\ end {align}\ nonumber\]

b. Para\(d_o=5.00\,cm\) e\(f=+10.0\,cm\)

\ [\ begin {align} d_i&=\ left (\ dfrac {1} {f} −\ dfrac {1} {d_o}\ direita) ^ {−1}\ nonumber \\ [4pt] &=\ left (\ dfrac {1} {10,0\, cm} −\ dfrac {1} {5,00\, cm}\ direita) ^ {−1}\ nonumber\\ [4pt] &=−10.0\, cm\ nonumber \ end {align}\ nonumber\]

A distância da imagem é negativa, então a imagem é virtual, está do mesmo lado da lente que o objeto e está a 10 cm da lente. A ampliação e a orientação da imagem são encontradas em

\ [\ begin {align} m &=−\ dfrac {d_i} {d_o}\ nonumber\\ [4pt] &=−\ dfrac {−10,0\, cm} {5,00\, cm}\ nonumber\\ [4pt] &=+2,00. \ nonumber\ end {align}\ nonumber\]

A ampliação positiva significa que a imagem está na vertical (ou seja, tem a mesma orientação do objeto). Desde então \(|m|>0\), a imagem é maior que o objeto. O tamanho da imagem é

\ [\ begin {align} |h_i|&=|m|h_o\ nonumber\\ [4pt] & =( 2,00) (3,0\, cm)\ nonumber\\ [4pt] &=6,0\, cm. \ nonumber \ end {align}\ nonumber\]

c. Para\(d_o=20\,cm\) e\(f=+10cm\)

\ [\ begin {align} d_i &= \ left (\ dfrac {1} {f} −\ dfrac {1} {d_o}\ direita) ^ {−1}\ nonumber\\ [4pt] &=\ left (\ dfrac {1} {10,0\, cm} −\ dfrac {1} {20,0\, cm}\ direita) ^ {−1} \ nonumber\\ [4pt] &=20,0\, cm\ nonumber\ end {align} \ nonumber\]

A distância da imagem é positiva, então a imagem é real, está no lado oposto da lente do objeto e está a 20,0 cm da lente. A ampliação é

\ [\ begin {align} m &=−\ dfrac {d_i} {d_o}\ nonumber\\ [4pt] &=−\ dfrac {20,0\, cm} {20,0\, cm}\ nonumber\\ [4pt] &=−1,00. \ nonumber\ end {align}\ nonumber\]

A ampliação negativa significa que a imagem está invertida. Desde então\(|m|=1\), a imagem tem o mesmo tamanho do objeto.

Ao resolver problemas em óptica geométrica, geralmente precisamos combinar o traçado de raios e as equações da lente. O exemplo a seguir demonstra essa abordagem.

Exemplo\(\PageIndex{3}\): Escolha da distância focal e do tipo de lente

Para projetar a imagem de uma lâmpada em uma tela a 1,50 m de distância, você precisa escolher o tipo de lente a ser usada (convergente ou divergente) e sua distância focal (Figura\(\PageIndex{12}\)). A distância entre a lente e a lâmpada é fixada em 0,75 m. Além disso, qual é a ampliação e a orientação da imagem?

A figura mostra uma lente biconvexa com distância focal de 0,5 metros e uma lâmpada colocada 0,75 metros na frente dela. Uma imagem invertida da lâmpada é formada em uma tela colocada 1,5 metros atrás da lente. — Figura\(\PageIndex{12}\): Uma lâmpada colocada a 0,75 m de uma lente com uma distância focal de 0,50 m produz uma imagem real em uma tela, conforme discutido no exemplo. O traçado de raios prevê a localização e o tamanho da imagem.

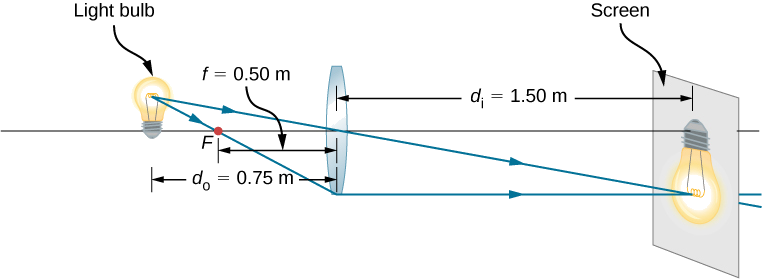
Estratégia

A imagem deve ser real, então você escolhe usar uma lente convergente. A distância focal pode ser encontrada usando a equação de lente fina e resolvendo a distância focal. A distância do objeto é \(d_o=0.75\,m\) e a distância da imagem é\(d_i=1.5\,m\).

Solução

Resolva a lente fina para a distância focal e insira as distâncias desejadas do objeto e da imagem:

\ [\ begin {align} \ dfrac {1} {d_o} +\ dfrac {1} {d_i} &=\ dfrac {1} {f}\ nonumber\\ [4pt] f &=\ left (\ dfrac {1} {d_o} +\ dfrac {1} {d_i}\ direita) ^ {−1} nonumber \\ [4pt] &= \ left (\ dfrac {1} {0,75\, m} +\ dfrac {1} {1,5\, m}\ direita) ^ {−1}\ nonumber \\[4pt] &= 0.50 \, m \nonumber \end{align} \nonumber \]

A ampliação é

\ [\ begin {align} m &=−\ dfrac {d_i} {d_o}\ nonumber\\ [4pt] &= −\ dfrac {1,5\, m} {0,75\, m}\ nonumber\\ [4pt] &=−2,0. \ nonumber \ end {align}\ nonumber\]

Significância

O sinal de menos para a ampliação significa que a imagem está invertida. A distância focal é positiva, conforme esperado para uma lente convergente. O traçado de raios pode ser usado para verificar o cálculo (Figura\(\PageIndex{12}\)). Como esperado, a imagem está invertida, é real e é maior do que o objeto.