2.4: Imagens formadas por refração

Last updated
Save as PDF

Page ID: 183218

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Descreva a formação da imagem por uma única superfície refratária
Determine a localização de uma imagem e calcule suas propriedades usando um diagrama de raios
Determine a localização de uma imagem e calcule suas propriedades usando a equação para uma única superfície refratária

Quando os raios de luz se propagam de um meio para outro, esses raios sofrem refração, que é quando as ondas de luz são curvadas na interface entre dois meios. A superfície refratária pode formar uma imagem de forma semelhante a uma superfície refletora, exceto que a lei da refração (lei de Snell) está no centro do processo e não na lei da reflexão.

Refração em uma interface plana—Profundidade aparente

Se você observar uma haste reta parcialmente submersa na água, ela parece se curvar na superfície. A razão por trás desse efeito curioso é que a imagem da haste dentro da água se forma um pouco mais perto da superfície do que a posição real da haste, portanto, ela não se alinha com a parte da haste que está acima da água. O mesmo fenômeno explica por que um peixe na água parece estar mais próximo da superfície do que realmente está.

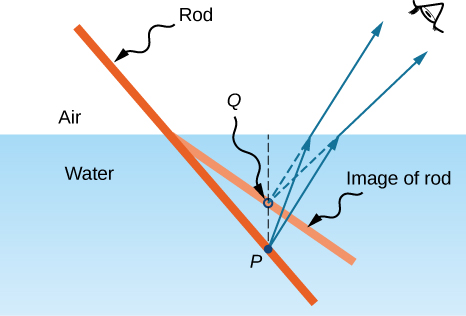
A figura mostra a vista lateral de uma haste mergulhada em água. Uma linha mais clara chamada imagem da haste é mostrada de tal forma que parece que a haste está dobrada na junção de ar e água. O ponto P está na haste e o ponto Q está na imagem da haste. Uma linha pontilhada PQ é mostrada perpendicularmente à superfície da água. Dois raios se originam de P, viajam para cima até a superfície da água, se curvam em um ângulo e alcançam o olho do observador. As extensões traseiras dos raios curvos parecem se originar do ponto Q. — Figura\(\PageIndex{1}\): Curvatura de uma haste em uma interface água-ar. O ponto\(P\) na haste parece estar no ponto\(Q\), que é onde a imagem do ponto P se forma devido à refração na interface ar-água.

Para estudar a formação de imagens como resultado da refração, considere as seguintes questões:

O que acontece com os raios de luz quando eles entram ou passam por um meio diferente?
Os raios refratados provenientes de um único ponto se encontram em algum ponto ou divergem um do outro?

Para ser concreto, consideramos um sistema simples que consiste em duas mídias separadas por uma interface plana (Figura\(\PageIndex{2}\)). O objeto está em um meio e o observador está no outro. Por exemplo, quando você olha para um peixe acima da superfície da água, o peixe está no meio 1 (a água) com índice de refração de 1,33, e seu olho está no meio 2 (o ar) com índice de refração 1,00, e a superfície da água é a interface. A profundidade que você “vê” é a altura da imagem\(h_i\) e é chamada de profundidade aparente. A profundidade real do peixe é a altura do objeto\(h_o\).

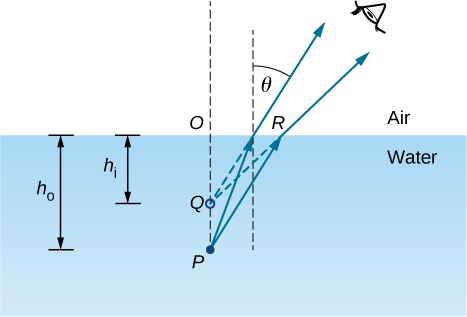
A figura mostra a vista lateral de alguma quantidade de água. O ponto P está dentro dele. Dois raios se originam do ponto P, se curvam na superfície da água e alcançam o olho do observador. As extensões posteriores desses raios refratados se cruzam no ponto Q. PQ é perpendicular à superfície da água e a cruza no ponto O. A distância OP é rotulada como h subscrito o e a distância OQ é rotulada como h subscrito i. O ângulo formado pelo raio refratado com uma linha perpendicular à superfície da água é rotulado como teta. — Figura\(\PageIndex{2}\): Profundidade aparente devido à refração. O objeto real no ponto P cria uma imagem no ponto Q. A imagem não está na mesma profundidade do objeto, então o observador vê a imagem em uma “profundidade aparente”.

A profundidade aparente h _i depende do ângulo em que você visualiza a imagem. Para uma visão de cima (a chamada visão “normal”), podemos aproximar o ângulo de refração\(θ\) para ser pequeno e substituir\(\sin θ\) na lei de Snell por\(\tan θ\). Com essa aproximação, você pode usar os triângulos\(ΔOPR\) e\(ΔOQR\) mostrar que a profundidade aparente é dada por

\[h_i= \left(\dfrac{n_2}{n_1}\right)h_o. \nonumber \]

A derivação desse resultado é deixada como um exercício. Assim, um peixe aparece a 3/4 da profundidade real quando visto de cima.

Refração em uma interface esférica

As formas esféricas desempenham um papel importante na óptica, principalmente porque formas esféricas de alta qualidade são muito mais fáceis de fabricar do que outras superfícies curvas. Para estudar a refração em uma única superfície esférica, assumimos que o meio com a superfície esférica em uma extremidade continua indefinidamente (um meio “semi-infinito”).

Refração em uma superfície convexa

Considere uma fonte pontual de luz no ponto P em frente a uma superfície convexa feita de vidro (Figura\(\PageIndex{3}\)). \(R\)Seja o raio de curvatura, n ₁ seja o índice de refração do meio no qual o ponto P do objeto está localizado e n ₂ seja o índice de refração do meio com a superfície esférica. Queremos saber o que acontece como resultado da refração nessa interface.

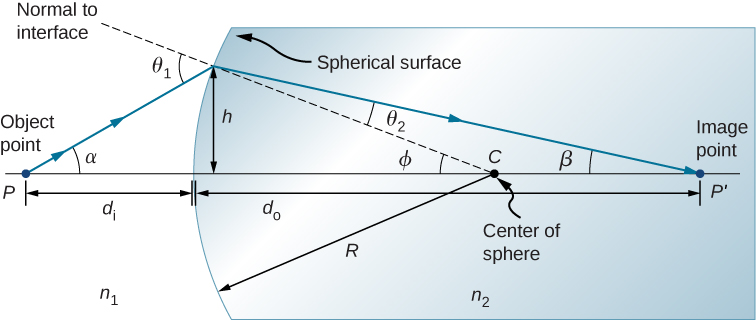
A figura mostra uma seção de uma esfera. O índice de refração do ar é n subscrito 1 e o da esfera é n subscrito 2. O centro da esfera é C e o raio é R. Um raio originado do ponto P no eixo óptico fora da esfera atinge a superfície convexa da esfera e é refratado dentro dela. Ele cruza o eixo no ponto P primo dentro da esfera, do outro lado do centro. Uma linha pontilhada chamada de normal para interface conecta o centro da esfera ao ponto de incidência. Ele faz um ângulo phi com o eixo óptico. Os raios incidente e refratado formam os ângulos alfa e beta, respectivamente, com o eixo óptico e os ângulos teta 1 e teta 2, respectivamente, com a interface normal. — Figura\(\PageIndex{3}\): Refração em uma superfície convexa (\(n_2>n_1\)).

Devido à simetria envolvida, basta examinar os raios em apenas um plano. A figura mostra um raio de luz que começa no ponto do objeto\(P\), refrata na interface e passa pelo ponto da imagem\(P′\). Derivamos uma fórmula que relaciona a distância do objeto\(d_o\), a distância\(d_i\) da imagem e o raio de curvatura\(R\).

Aplicar a lei de Snell ao raio que emana do ponto\(P\) dá

\[n_1\sin θ_1=n_2 \sin θ_2. \nonumber \]

Dentro da aproximação de pequeno ângulo

\[\sin θ≈θ, \nonumber \]

A lei de Snell então assume a forma

\[n_1θ_1≈n_2θ_2. \label{eq8} \]

A partir da geometria da Figura\(\PageIndex{3}\), vemos que

\[θ_1=α+ϕ, \nonumber \]

\[θ_2=ϕ−β. \nonumber \]

A inserção de ambas as expressões na Equação\ ref {eq8} dá

\[n_1(α+ϕ)≈n_2(ϕ−β). \label{eq10} \]

Usando a Figura\(\PageIndex{3}\), calculamos a tangente dos ângulos\(α\),\(β\), e\(ϕ\):

\(\tan α≈\dfrac{h}{d_o}\)
\(\tan β≈\dfrac{h}{d_i}\)
\(\tan ϕ≈\dfrac{h}{R}\)

Novamente, usando a aproximação de pequeno ângulo, descobrimos que\(\tan θ≈ θ\), então, as relações acima se tornam

\(α≈\dfrac{h}{d_o}\)
\(~β≈\dfrac{h}{d_i}\)
\(~ϕ≈\dfrac{h}{R}.\)

Colocar esses ângulos na Equação\ ref {eq10} dá

\[n_1\left(\dfrac{h}{d_o}+\dfrac{h}{R}\right)=n_2 \left(\dfrac{h}{R}−\dfrac{h}{d_i}\right). \nonumber \]

Podemos escrever isso de forma mais conveniente, pois

\[\dfrac{n_1}{d_o}+\dfrac{n_2}{d_i}=\dfrac{n_2−n_1}{R}. \label{eq20} \]

Se o objeto for colocado em um ponto especial chamado primeiro foco, ou foco do objeto\(F_1\), a imagem será formada no infinito, conforme mostrado na Figura\(\PageIndex{4a}\).

A Figura a mostra uma seção de uma esfera e um ponto F1 fora dela, no eixo óptico. Os raios provenientes de F1 atingem a superfície convexa e são refratados dentro da esfera como raios paralelos. A distância de F1 da superfície é f subscrito 1. A Figura b mostra raios paralelos ao eixo óptico atingindo a superfície convexa e sendo refratados. Eles convergem no ponto F2 dentro da esfera. F2 fica no eixo óptico entre a superfície e o centro da esfera. A distância de F2 da superfície é f subscrito 2. Em ambas as figuras, o índice de refração do ar é n1 e o da esfera é n2 maior que n1. — Figura\(\PageIndex{4}\): (a) Primeiro foco (chamado de “foco do objeto”) para refração em uma superfície convexa. (b) Segundo foco (chamado de “foco de imagem”) para refração em uma superfície convexa.

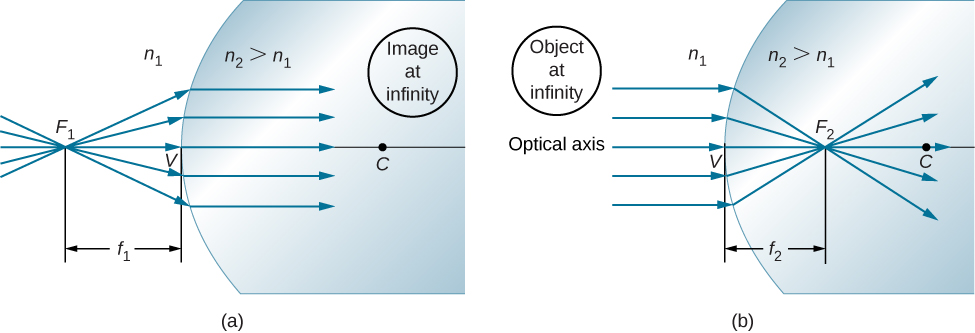
Podemos encontrar a localização\(f_1\) do primeiro foco\(F_1\) configurando\(d_i=\infty\) em Equação\ ref {eq20}.

\[ \begin{align} \dfrac{n_1}{f_1}+\dfrac{n_2}{\infty} &=\dfrac{n_2−n_1}{R} \\[4pt] f_1 &=\dfrac{n_1R}{n_2−n_1} \end{align} \nonumber \]

Da mesma forma, podemos definir um segundo foco ou foco de imagem\(F_2\) onde a imagem é formada para um objeto distante (Figura\(\PageIndex{4b}\)). A localização do segundo foco\(F_2\) é obtida na Equação\ ref {eq20} configurando\(d_0=\infty\):

\[ \begin{align} \dfrac{n_1}{\infty}+\dfrac{n_2}{f_2}=\dfrac{n_2−n_1}{R} \\[4pt] f_2=\dfrac{n_2R}{n_2−n_1}. \end{align} \nonumber \]

Observe que o foco do objeto está a uma distância diferente do vértice do foco da imagem porque\(n_1≠n_2\).

Convenção de sinalização para superfícies de refração única

Embora tenhamos derivado essa equação para refração em uma superfície convexa, a mesma expressão vale para uma superfície côncava, desde que usemos a seguinte convenção de sinais:

\(R>0\)se a superfície for convexa em direção ao objeto; caso contrário,\(R<0\).
\(d_i>0\)se a imagem for real e estiver no lado oposto do objeto; caso contrário,\(d_i<0\).