2.3: Espelhos esféricos

Objetivos de

Ao final desta seção, você poderá:

• Descreva a formação de imagens por espelhos esféricos.
• Use diagramas de raios e a equação do espelho para calcular as propriedades de uma imagem em um espelho esférico.

A imagem em um espelho plano tem o mesmo tamanho do objeto, é vertical e está à mesma distância atrás do espelho que o objeto está na frente do espelho. Um espelho curvo, por outro lado, pode formar imagens maiores ou menores que o objeto e podem se formar na frente do espelho ou atrás dele. Em geral, qualquer superfície curva formará uma imagem, embora algumas imagens fiquem tão distorcidas a ponto de ficarem irreconhecíveis (pense em espelhos domésticos divertidos). Como os espelhos curvos podem criar uma variedade tão rica de imagens, eles são usados em muitos dispositivos ópticos que têm muitos usos. Vamos nos concentrar em espelhos esféricos em sua maior parte, porque eles são mais fáceis de fabricar do que espelhos como espelhos parabólicos e, portanto, são mais comuns.

Espelhos curvos

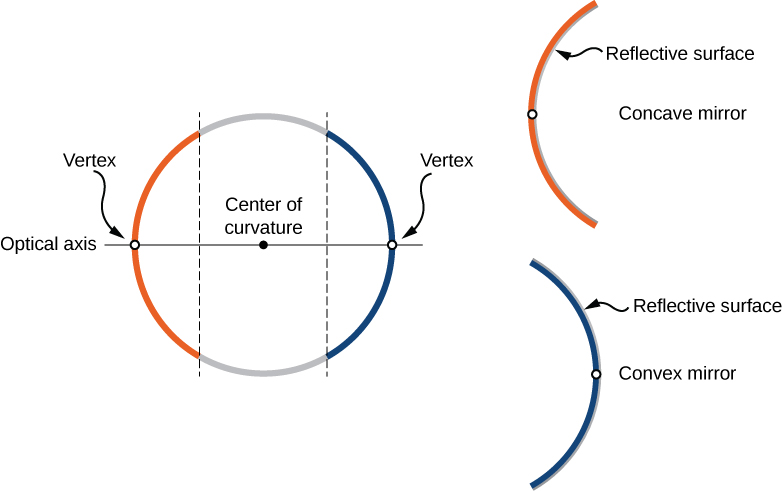
Podemos definir dois tipos gerais de espelhos esféricos. Se a superfície refletora for o lado externo da esfera, o espelho é chamado de espelho convexo. Se a superfície interna for a superfície refletora, ela é chamada de espelho côncavo.

A simetria é uma das principais características de muitos dispositivos ópticos, incluindo espelhos e lentes. O eixo de simetria desses elementos ópticos é frequentemente chamado de eixo principal ou eixo óptico. Para um espelho esférico, o eixo óptico passa pelo centro de curvatura do espelho e pelo vértice do espelho, conforme mostrado na Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\). Um espelho esférico é formado cortando um pedaço de uma esfera e prateando a superfície interna ou externa. Um espelho côncavo tem prata na superfície interna (pense em “caverna”) e um espelho convexo tem prata na superfície externa.

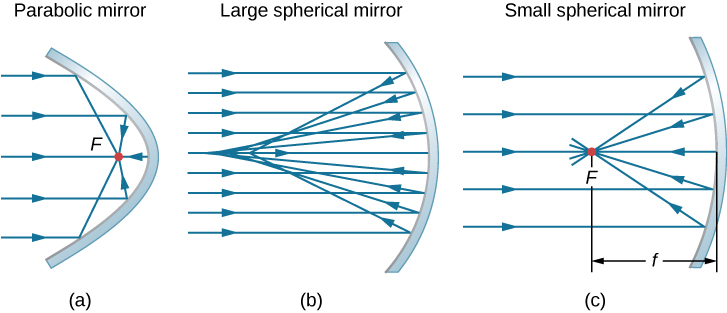
Considere os raios que são paralelos ao eixo óptico de um espelho parabólico, conforme mostrado na Figura\(\PageIndex{2a}\). Seguindo a lei da reflexão, esses raios são refletidos de forma que converjam em um ponto, chamado ponto focal. A figura\(\PageIndex{2b}\) mostra um espelho esférico que é grande em comparação com seu raio de curvatura. Para esse espelho, os raios refletidos não se cruzam no mesmo ponto, então o espelho não tem um ponto focal bem definido. Isso é chamado de aberração esférica e resulta em uma imagem borrada de um objeto estendido. A figura\(\PageIndex{2c}\) mostra um espelho esférico que é pequeno em comparação com seu raio de curvatura. Esse espelho é uma boa aproximação de um espelho parabólico, então os raios que chegam paralelamente ao eixo óptico são refletidos em um ponto focal bem definido. A distância ao longo do eixo óptico do espelho até o ponto focal é chamada de distância focal do espelho.

Figura\(\PageIndex{2}\): (a) Raios paralelos refletidos por um espelho parabólico se cruzam em um único ponto chamado ponto focal F. (b) Raios paralelos refletidos por um grande espelho esférico não se cruzam em um ponto comum. (c) Se um espelho esférico é pequeno em comparação com seu raio de curvatura, ele se aproxima melhor da parte central de um espelho parabólico, então raios paralelos essencialmente se cruzam em um ponto comum. A distância ao longo do eixo óptico do espelho até o ponto focal é a distância focal f do espelho.

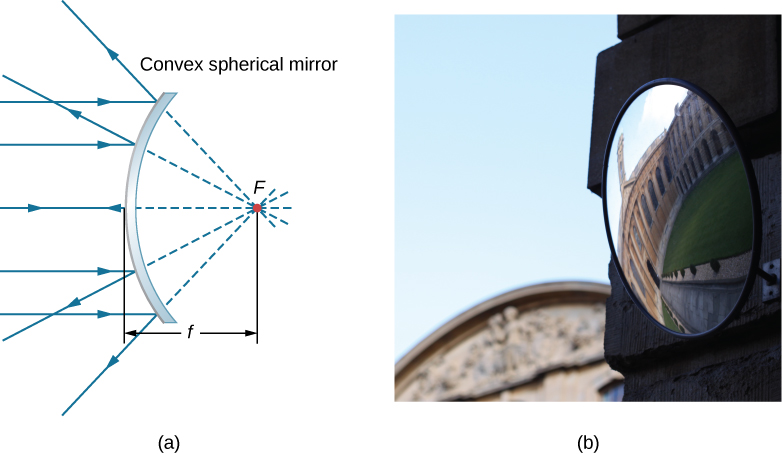
Um espelho esférico convexo também tem um ponto focal, conforme mostrado na Figura\(\PageIndex{3}\). Os raios incidentes paralelos ao eixo óptico são refletidos pelo espelho e parecem se originar de um ponto\(F\) na distância focal\(f\) atrás do espelho. Assim, o ponto focal é virtual porque nenhum raio real realmente passa por ele; eles só parecem se originar dele.

Figura\(\PageIndex{3}\): (a) Raios refletidos por um espelho esférico convexo: Raios incidentes de luz paralelos ao eixo óptico são refletidos por um espelho esférico convexo e parecem se originar de um ponto focal bem definido à distância focal f no lado oposto do espelho. O ponto focal é virtual porque nenhum raio real passa por ele. (b) Fotografia de uma imagem virtual formada por um espelho convexo. (crédito b: modificação da obra de Jenny Downing)

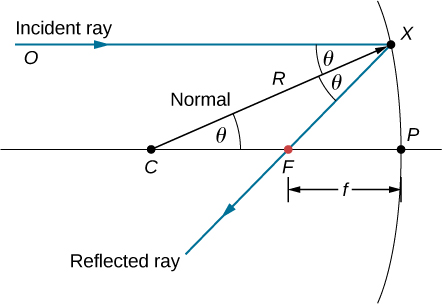
Como a distância focal de um espelho se relaciona com o raio de curvatura do espelho? A figura\(\PageIndex{4}\) mostra um único raio que é refletido por um espelho côncavo esférico. O raio incidente é paralelo ao eixo óptico. O ponto em que o raio refletido cruza o eixo óptico é o ponto focal. Observe que todos os raios incidentes que são paralelos ao eixo óptico são refletidos pelo ponto focal — mostramos apenas um raio para simplificar. Queremos descobrir como a distância focal\(FP\) (indicada por\(f\)) se relaciona com o raio de curvatura do espelho,\(R\), cujo comprimento é

\[R=CF+FP. \label{eq31} \]

A lei da reflexão nos diz que os ângulos\(\angle OXC\) e\(\angle CXF\) são os mesmos, e como o raio incidente é paralelo ao eixo óptico,\(\angle OXC\) os ângulos também\(\angle XCP\) são os mesmos. Assim, triângulo\(CXF\) é um triângulo isósceles com\(CF=FX\). Se o ângulo\(θ\) for pequeno, então

\[\sin θ≈ θ \label{sma} \]

que é chamada de “aproximação de pequeno ângulo”), então\(FX≈FP\) ou\(CF≈FP\). Inserindo isso na Equação\ ref {eq31} para o raio\(R\), obtemos

\[\begin{align} R &=CF+FP \nonumber \\[4pt] &=FP+FP \nonumber \\[4pt] &=2FP\nonumber \\[4pt] &=2f \end{align} \nonumber \]

Em outras palavras, na aproximação de pequeno ângulo, a distância focal\(f\) de um espelho esférico côncavo é metade de seu raio de curvatura,\(R\):

\[f=\dfrac{R}{2}. \nonumber \]

Neste capítulo, assumimos que a aproximação de pequeno ângulo (também chamada de aproximação paraxial) é sempre válida. Nessa aproximação, todos os raios são raios paraxiais, o que significa que eles formam um pequeno ângulo com o eixo óptico e estão a uma distância muito menor que o raio de curvatura do eixo óptico. Nesse caso, seus ângulos\(θ\) de reflexão são ângulos pequenos, então

\[\sin θ≈ \tan θ≈ θ. \label{smallangle} \]

Figura\(\PageIndex{4}\): Reflexão em um espelho côncavo. Na aproximação de pequeno ângulo, um raio paralelo ao eixo óptico CP é refletido pelo ponto focal F do espelho.

Usando o Ray Tracing para localizar imagens

Para encontrar a localização de uma imagem formada por um espelho esférico, primeiro usamos o traçado de raios, que é a técnica de desenhar raios e usar a lei da reflexão para determinar os raios refletidos (posteriormente, para lentes, usamos a lei da refração para determinar os raios refratados). Combinado com alguma geometria básica, podemos usar o traçado de raios para encontrar o ponto focal, a localização da imagem e outras informações sobre como um espelho manipula a luz. Na verdade, já usamos o traçado de raios acima para localizar o ponto focal dos espelhos esféricos ou a distância da imagem de espelhos planos. Para localizar a imagem de um objeto, você deve localizar pelo menos dois pontos da imagem. Localizar cada ponto requer desenhar pelo menos dois raios de um ponto no objeto e construir seus raios refletidos. O ponto em que os raios refletidos se cruzam, seja no espaço real ou no espaço virtual, é onde o ponto correspondente da imagem está localizado. Para facilitar o traçado de raios, nos concentramos em quatro raios “principais” cujos reflexos são fáceis de construir.

\(\PageIndex{5}\)A figura mostra um espelho côncavo e um espelho convexo, cada um com um objeto em forma de seta à sua frente. Esses são os objetos cujas imagens queremos localizar por traçado de raios. Para fazer isso, desenhamos raios do ponto\(Q\) que está no objeto, mas não no eixo óptico. Escolhemos desenhar nosso raio a partir da ponta do objeto. O raio principal 1 vai do ponto\(Q\) e viaja paralelamente ao eixo óptico. O reflexo desse raio deve passar pelo ponto focal, conforme discutido acima. Assim, para o espelho côncavo, a reflexão do raio principal 1 passa pelo ponto focal\(F\), conforme mostrado na Figura\(\PageIndex{5b}\). Para o espelho convexo, a extensão inversa da reflexão do raio principal 1 passa pelo ponto focal (ou seja, um foco virtual). O raio principal 2 viaja primeiro na linha que passa pelo ponto focal e depois é refletido de volta ao longo de uma linha paralela ao eixo óptico. O raio principal 3 viaja em direção ao centro de curvatura do espelho, então ele atinge o espelho em uma incidência normal e é refletido de volta ao longo da linha de onde veio. Finalmente, o raio principal 4 atinge o vértice do espelho e é refletido simetricamente em torno do eixo óptico.

Figura\(\PageIndex{5}\): Os quatro raios principais mostrados para (a) um espelho côncavo e (b) um espelho convexo. A imagem se forma onde os raios se cruzam (para imagens reais) ou onde suas extensões para trás se cruzam (para imagens virtuais).

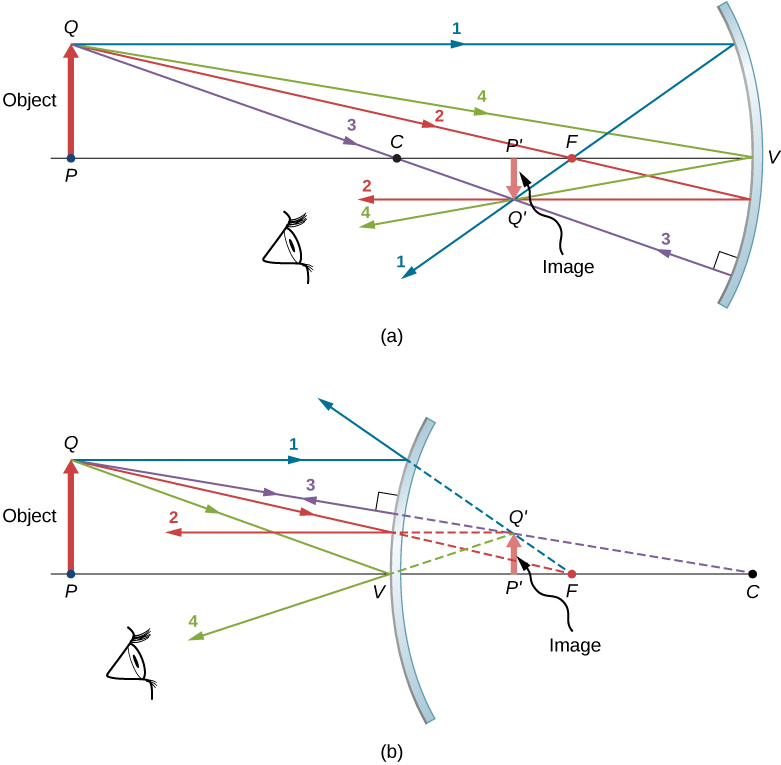
Os quatro raios principais se cruzam no ponto\(Q′\), que é onde a imagem do ponto\(Q\) está localizada. Para localizar o ponto\(Q′\), desenhar quaisquer dois desses raios principais seria suficiente. Portanto, somos livres para escolher qualquer um dos raios principais que desejamos para localizar a imagem. Desenhar mais de dois raios principais às vezes é útil para verificar se o traçado do raio está correto.

Para localizar completamente a imagem estendida, precisamos localizar um segundo ponto na imagem, para que saibamos como a imagem está orientada. Para fazer isso, traçamos os raios principais da base do objeto. Nesse caso, todos os quatro raios principais correm ao longo do eixo óptico, refletem no espelho e, em seguida, correm de volta ao longo do eixo óptico. A dificuldade é que, como esses raios são colineares, não podemos determinar um ponto único onde eles se cruzam. Tudo o que sabemos é que a base da imagem está no eixo óptico. No entanto, como o espelho é simétrico de cima para baixo, ele não altera a orientação vertical do objeto. Assim, como o objeto é vertical, a imagem deve ser vertical. Portanto, a imagem da base do objeto está no eixo óptico diretamente acima da imagem da ponta, conforme desenhado na figura.

Para o espelho côncavo, a imagem estendida nesse caso se forma entre o ponto focal e o centro de curvatura do espelho. É invertido em relação ao objeto, é uma imagem real e é menor que o objeto. Se movêssemos o objeto para mais perto ou para mais longe do espelho, as características da imagem mudariam. Por exemplo, mostramos, como um exercício posterior, que um objeto colocado entre um espelho côncavo e seu ponto focal leva a uma imagem virtual que é vertical e maior que o objeto. Para o espelho convexo, a imagem estendida se forma entre o ponto focal e o espelho. É vertical em relação ao objeto, é uma imagem virtual e é menor que o objeto.

Regras de Ray-Tracing

O traçado de raios é muito útil para espelhos. As regras para traçado de raios estão resumidas aqui para referência:

• Um raio viajando paralelamente ao eixo óptico de um espelho esférico é refletido ao longo de uma linha que passa pelo ponto focal do espelho (raio 1 na Figura\(\PageIndex{5}\)).
• Um raio viajando ao longo de uma linha que passa pelo ponto focal de um espelho esférico é refletido ao longo de uma linha paralela ao eixo óptico do espelho (raio 2 na Figura\(\PageIndex{5}\)).
• Um raio viajando ao longo de uma linha que passa pelo centro de curvatura de um espelho esférico é refletido de volta ao longo da mesma linha (raio 3 na Figura\(\PageIndex{5}\)).
• Um raio que atinge o vértice de um espelho esférico é refletido simetricamente sobre o eixo óptico do espelho (raio 4 na Figura\(\PageIndex{5}\)).

Usamos o traçado de raios para ilustrar como as imagens são formadas por espelhos e para obter informações numéricas sobre as propriedades ópticas do espelho. Se assumirmos que um espelho é pequeno em comparação com seu raio de curvatura, também podemos usar álgebra e geometria para derivar uma equação de espelho, o que faremos na próxima seção. Combinar o traçado de raios com a equação do espelho é uma boa maneira de analisar sistemas de espelhos.

Formação de imagem por reflexão—A equação do espelho

Para um espelho plano, mostramos que a imagem formada tem a mesma altura e orientação do objeto e está localizada à mesma distância atrás do espelho que o objeto está na frente do espelho. Embora a situação seja um pouco mais complicada para espelhos curvos, o uso da geometria leva a fórmulas simples que relacionam as distâncias do objeto e da imagem às distâncias focais dos espelhos côncavos e convexos.

Figura\(\PageIndex{6}\): Imagem formada por um espelho côncavo.

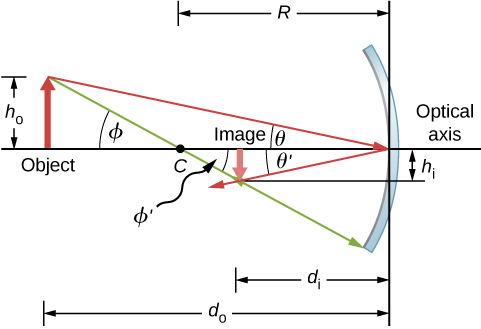
Considere o objeto\(OP\) mostrado na Figura\(\PageIndex{6}\). O centro de curvatura do espelho é rotulado\(C\) e está a uma\(R\) distância do vértice do espelho, conforme marcado na figura. As distâncias do objeto e da imagem são rotuladas\(d_o\) e\(d_i\) as alturas do objeto e da imagem são rotuladas\(h_o\) e\(h_i\), respectivamente. Como os ângulos\(ϕ\) e\(ϕ′\) são ângulos internos alternativos, sabemos que eles têm a mesma magnitude. No entanto, eles devem diferir no sinal se medirmos os ângulos do eixo óptico, então\(ϕ=−ϕ′\). Um cenário análogo vale para os ângulos\(θ\)\(θ′\) e. A lei da reflexão nos diz que eles têm a mesma magnitude, mas seus sinais devem diferir se medirmos os ângulos do eixo óptico. Assim,\(θ=−θ′\). Tomando a tangente dos ângulos\(θ\) e\(θ′\), e usando a propriedade que\(\tan(−θ)=−\tan θ\), nos dá

\[\left. \begin{array}{rcl} \tanθ=\dfrac{h_o}{d_o} \\ \tanθ′=−\tanθ=\dfrac{h_i}{d_i} \end{array}\right\} =\dfrac{h_o}{d_o}=−\dfrac{h_i}{d_i} \label{eq51} \]

ou

\[- \dfrac{h_o}{h_i}=\dfrac{d_o}{d_i}.\label{eq52} \]

Da mesma forma, tomando a tangente de\(ϕ\) e\(ϕ′\) dá

\[\left. \begin{array}{rcl} \tanϕ=\dfrac{h_o}{d_o-R} \\ \tanϕ′=−\tanϕ=\dfrac{h_i}{R-d_i} \end{array}\right\} =\dfrac{h_o}{d_o-R}=−\dfrac{h_i}{R-d_i} \nonumber \]

ou

\[−\dfrac{h_o}{h_i}=\dfrac{d_o-R}{R-d_i}. \label{eq55} \]

A combinação da Equação\ ref {eq51} e\ ref {eq55} dá

\[\dfrac{d_o}{d_i}=\dfrac{d_o−R}{R−d_i}. \nonumber \]

Depois de um pouco de álgebra, isso se torna

\[\dfrac{1}{d_o}+\dfrac{1}{d_i}=\dfrac{2}{R}. \label{eq57} \]

Nenhuma aproximação é necessária para esse resultado, então é exato. No entanto, conforme discutido acima, na aproximação de pequeno ângulo, a distância focal de um espelho esférico é metade do raio de curvatura do espelho, ou\(f=R/2\). Ao inserir isso na Equação\ ref {eq57}, obtém-se a equação do espelho:

\[\underbrace{ \dfrac{1}{d_o}+\dfrac{1}{d_i}=\dfrac{1}{f}}_{\text{mirror equation}}. \label{mirror equation} \]

A equação do espelho relaciona as distâncias da imagem e do objeto com a distância focal e é válida somente na aproximação de pequeno ângulo (Equação\ ref {sma}). Embora tenha sido derivado de um espelho côncavo, ele também vale para espelhos convexos (provando que isso é deixado como um exercício). Podemos estender a equação do espelho para o caso de um espelho plano observando que um espelho plano tem um raio de curvatura infinito. Isso significa que o ponto focal está no infinito, então a equação do espelho simplifica para

\[d_o=−d_i \nonumber \]

que é a mesma equação obtida anteriormente.

Observe que temos sido muito cuidadosos com os sinais ao derivar a equação do espelho. Para um espelho plano, a distância da imagem tem o sinal oposto da distância do objeto. Além disso, a imagem real formada pelo espelho côncavo na Figura\(\PageIndex{6}\) está no lado oposto do eixo óptico em relação ao objeto. Nesse caso, a altura da imagem deve ter o sinal oposto da altura do objeto. Para acompanhar os sinais das várias quantidades na equação do espelho, agora introduzimos uma convenção de sinais.

Convenção de sinalização para espelhos esféricos

Usar uma convenção de sinais consistente é muito importante na óptica geométrica. Ele atribui valores positivos ou negativos às quantidades que caracterizam um sistema óptico. Entender a convenção de sinais permite que você descreva uma imagem sem construir um diagrama de raios. Este texto usa a seguinte convenção de sinais:

1. A distância focal\(f\) é positiva para espelhos côncavos e negativa para espelhos convexos.
2. A distância da imagem\(d_i\) é positiva para imagens reais e negativa para imagens virtuais.

Observe que a regra 1 significa que o raio de curvatura de um espelho esférico pode ser positivo ou negativo. O que significa ter um raio de curvatura negativo? Isso significa simplesmente que o raio de curvatura de um espelho convexo é definido como negativo.

Ampliação da imagem

Vamos usar a convenção de sinais para interpretar melhor a derivação da equação do espelho. Ao derivar essa equação, descobrimos que as alturas do objeto e da imagem estão relacionadas por

\[−\dfrac{h_o}{h_i}=\dfrac{d_o}{d_i}. \label{eq61} \]

Veja a Equação\ ref {eq52}. Tanto o objeto quanto a imagem formada pelo espelho na Figura\(\PageIndex{6}\) são reais, então as distâncias do objeto e da imagem são positivas. O ponto mais alto do objeto está acima do eixo óptico, então a altura do objeto é positiva. A imagem, no entanto, está abaixo do eixo óptico, então a altura da imagem é negativa. Assim, essa convenção de sinais é consistente com nossa derivação da equação do espelho.

A equação\ ref {eq61} na verdade descreve a ampliação linear (geralmente chamada simplesmente de “ampliação”) da imagem em termos das distâncias do objeto e da imagem. Assim, definimos a ampliação adimensional da\(m\) seguinte forma:

\[\underbrace{m=\dfrac{h_i}{h_o}}_{\text{linear magnification}}. \label{mag} \]

Se\(m\) for positivo, a imagem está na vertical e, se\(m\) for negativo, a imagem será invertida. Se\(|m|>1\), a imagem for maior que o objeto e, se\(|m|<1\), a imagem for menor que o objeto. Com essa definição de ampliação, obtemos a seguinte relação entre as distâncias vertical e horizontal do objeto e da imagem:

\[m=\dfrac{h_i}{h_o}=−\dfrac{d_i}{d_o}. \nonumber \]

Essa é uma relação muito útil porque permite obter a ampliação da imagem do objeto e as distâncias da imagem, que você pode obter da equação do espelho.

Exemplo\(\PageIndex{1}\): Solar Electric Generating System

Uma das tecnologias solares usadas atualmente para gerar eletricidade envolve um dispositivo (chamado de calha parabólica ou coletor de concentração) que concentra a luz solar em um tubo enegrecido que contém um fluido. Esse fluido aquecido é bombeado para um trocador de calor, onde a energia térmica é transferida para outro sistema que é usado para gerar vapor e, eventualmente, gera eletricidade por meio de um ciclo de vapor convencional. A figura\(\PageIndex{7}\) mostra esse sistema de trabalho no sul da Califórnia. O espelho real é um cilindro parabólico com seu foco localizado no tubo; no entanto, podemos aproximar o espelho como exatamente um quarto de um cilindro circular.

Figura\(\PageIndex{7}\): Coletores de calhas parabólicas são usados para gerar eletricidade no sul da Califórnia. (crédito: “kjkolb” /Wikimedia Commons)

1. Se quisermos que os raios do sol se concentrem a 40,0 cm do espelho, qual é o raio do espelho?
2. Qual é a quantidade de luz solar concentrada no tubo, por metro de comprimento do tubo, assumindo que a insolação (radiação solar incidente) é de 900 W/m ²?
3. Se o tubo de transporte de fluido tiver um diâmetro de 2,00 cm, qual é o aumento de temperatura do fluido por metro de tubo durante um período de 1 minuto? Suponha que toda a radiação solar incidente no refletor seja absorvida pelo tubo e que o fluido seja óleo mineral.

Estratégia

Primeiro identifique os princípios físicos envolvidos. A parte (a) está relacionada à ótica dos espelhos esféricos. A parte (b) envolve um pouco de matemática, principalmente geometria. A parte (c) requer uma compreensão do calor e da densidade.

Solução

a. O sol é o objeto, então a distância do objeto é essencialmente infinita:\(d_o=\infty\). A distância desejada da imagem é\(d_i=40.0\,cm\). Usamos a equação do espelho (Equação\ ref {equação do espelho}) para encontrar a distância focal do espelho:

\[\begin{align*} \dfrac{1}{d_o}+\dfrac{1}{d_i} &=\dfrac{1}{f} \nonumber \\[4pt] f &= \left(\dfrac{1}{d_o}+\dfrac{1}{d_i}\right)^{−1} \\[4pt] &= \left(\dfrac{1}{\infty}+\dfrac{1}{40.0\,cm}\right)^{−1} \\[4pt] &= 40.0 \,cm \end{align*} \nonumber \]

Assim, o raio do espelho é

\[R=2f=80.0\,cm. \nonumber \]

b. A insolação é de 900 W/m ². Você deve encontrar a área\(A\) da seção transversal do espelho côncavo, pois a energia fornecida é\(900\, W/m^2×A\). O espelho, neste caso, é um quarto de seção de um cilindro, então a área\(L\) de um comprimento do espelho é\(A=\frac{1}{4}(2πR)L\). A área para um comprimento de 1,00 m é então

\[\begin{align*} A&=\dfrac{\pi}{2}R(1.00m) \\[4pt] &=\dfrac{(3.14)}{2}(0.800\,m)(1.00\,m) \\[4pt] &=1.26\,m^2. \end{align*} \nonumber \]

A insolação no comprimento de 1,00 m do tubo é então

\[(9.00×10^2\dfrac{W}{m^2})(1.26\,m^2)=1130\,W. \nonumber \]

c. O aumento da temperatura é dado por\(Q=mcΔT\). A massa\(m\) do óleo mineral na seção de um metro do tubo é

\[ \begin{align*} m &= ρV = ρπ\left(\dfrac{d}{2}\right)^2(1.00\,m) \nonumber \\[4pt] &=(8.00×10^2kg/m^3)(3.14)(0.0100\,m)^2(1.00\,m) \nonumber \\[4pt] &=0.251\,kg \end{align*} \nonumber \]

Portanto, o aumento da temperatura em um minuto é

\[ \begin{align*} \Delta T&= \dfrac{Q}{mc} \nonumber \\[4pt] &=\dfrac{(1130\,W)(60.0\,s)}{(0.251\,kg)(1670\,J⋅kg/°C)} \nonumber \\[4pt] &=162°\end{align*} \nonumber \]

Significância

Uma série desses tubos no deserto da Califórnia pode fornecer uma potência térmica de 250 MW em um dia ensolarado, com fluidos atingindo temperaturas de até 400° C. Estamos considerando apenas um metro de tubo aqui e ignorando as perdas de calor ao longo do tubo.

Exemplo\(\PageIndex{2}\): Image in a Convex Mirror

Um ceratômetro é um dispositivo usado para medir a curvatura da córnea do olho, particularmente para ajustar lentes de contato. A luz é refletida pela córnea, que age como um espelho convexo, e o ceratômetro mede a ampliação da imagem. Quanto menor a ampliação, menor o raio de curvatura da córnea. Se a fonte de luz estiver a 12 cm da córnea e a ampliação da imagem for 0,032, qual é o raio de curvatura da córnea?

Estratégia

Se você encontrar a distância focal do espelho convexo formado pela córnea, então você conhece seu raio de curvatura (é o dobro da distância focal). A distância do objeto é d _o = 12cm e a ampliação é m = 0,032. Primeiro, encontre a distância da imagem\(d_i\) e depois resolva a distância focal\(f\).

Solução

Comece com a equação para ampliação (Equation\ ref {mag}) e resolvendo\(d_i\) e inserindo os valores fornecidos produz

\[d_i=−m d_o=−(0.032)(12\,cm)=−0.384\,cm \nonumber \]

onde mantivemos um valor extra significativo porque essa é uma etapa intermediária no cálculo. Resolva a equação do espelho para a distância focal\(f\) e insira os valores conhecidos para as distâncias do objeto e da imagem. O resultado é

\[ \begin{align*} \dfrac{1}{d_o}+\dfrac{1}{d_i} &= \dfrac{1}{f} \\[4pt] f &= \left(\dfrac{1}{d_o}+\dfrac{1}{d_i}\right)^{−1}  \\[4pt] &= \left(\dfrac{1}{12cm}+\dfrac{1}{-0.384cm}\right)^{−1} \\[4pt] &=-40.0 \,cm \end{align*} \nonumber \]

O raio de curvatura é o dobro da distância focal, então

\[R=2f=−0.80\,cm \nonumber \]

Significância

A distância focal é negativa, então o foco é virtual, como esperado para um espelho côncavo e um objeto real. O raio de curvatura encontrado aqui é razoável para uma córnea. A distância da córnea à retina em um olho adulto é de cerca de 2,0 cm. Na prática, as córneas podem não ser esféricas, o que complica o trabalho de ajustar as lentes de contato. Observe que a distância da imagem aqui é negativa, consistente com o fato de a imagem estar atrás do espelho. Assim, a imagem é virtual porque nenhum raio realmente passa por ela. Nos problemas e exercícios, você mostrará que, para uma distância fixa de objeto, um raio de curvatura menor corresponde a uma ampliação menor.

ESTRATÉGIA DE RESOLUÇÃO DE PROBLEMAS: ESPELHOS ESFÉRICOS

• Etapa 1. Primeiro, certifique-se de que a formação da imagem por um espelho esférico esteja envolvida.
• Etapa 2. Determine se o traçado de raios, a equação do espelho ou ambos são necessários. Um esboço é muito útil mesmo que o traçado de raios não seja especificamente exigido pelo problema. Escreva símbolos e valores conhecidos no esboço.
• Etapa 3. Identifique exatamente o que precisa ser determinado no problema (identifique as incógnitas).
• Etapa 4. Faça uma lista do que é dado ou pode ser inferido do problema conforme declarado (identifique os conhecidos).
• Etapa 5. Se o traçado de raios for necessário, use as regras de traçado de raios listadas no início desta seção.
• Etapa 6. A maioria dos problemas quantitativos requer o uso da equação do espelho. Use os exemplos como guias para usar a equação do espelho.
• Etapa 7. Verifique se a resposta faz sentido. Os sinais de distância do objeto, distância da imagem e distância focal correspondem ao que se espera do traçado de raios? O sinal da ampliação está correto? As distâncias do objeto e da imagem são razoáveis?

Partida da aproximação de pequeno ângulo

A aproximação de pequeno ângulo (Equation\ ref {smallangle}) é a base da discussão acima sobre a formação de imagens por um espelho esférico. Quando essa aproximação é violada, a imagem criada por um espelho esférico fica distorcida. Essa distorção é chamada de aberração. Aqui, discutimos brevemente dois tipos específicos de aberrações: aberração esférica e coma.

Aberração esférica

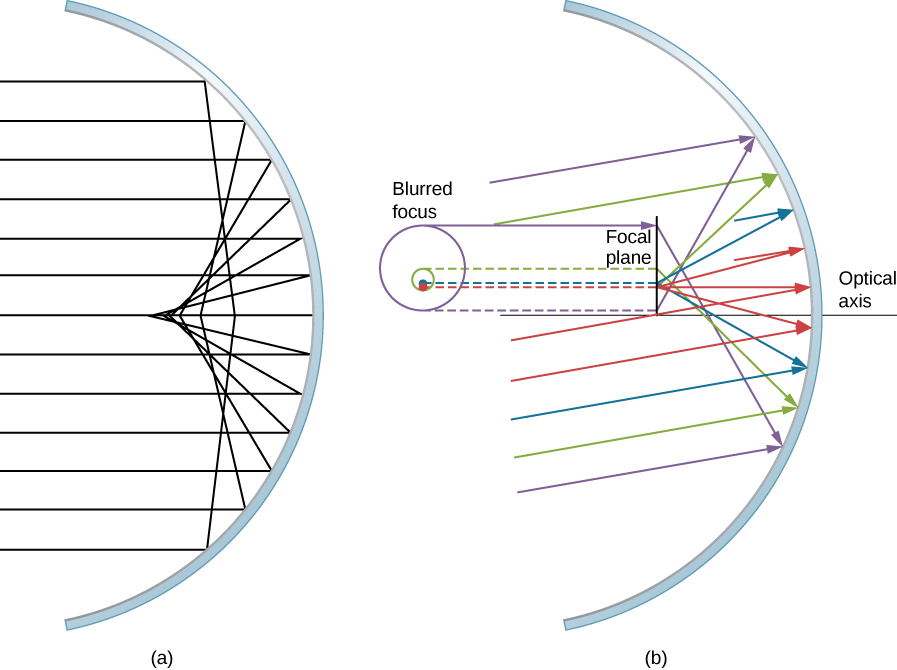
Considere um amplo feixe de raios paralelos colidindo com um espelho esférico, conforme mostrado na Figura\(\PageIndex{8}\). Quanto mais longe do eixo óptico os raios atingem, pior o espelho esférico se aproxima de um espelho parabólico. Assim, esses raios não são focados no mesmo ponto que os raios próximos ao eixo óptico, conforme mostrado na figura. Por causa da aberração esférica, a imagem de um objeto estendido em um espelho esférico ficará desfocada. As aberrações esféricas são características dos espelhos e lentes que consideramos na seção seguinte deste capítulo (espelhos e lentes mais sofisticados são necessários para eliminar aberrações esféricas).

Figura\(\PageIndex{8}\): (a) Com a aberração esférica, os raios que estão mais distantes do eixo óptico e os raios que estão mais próximos do eixo óptico são focados em pontos diferentes. Observe que a aberração piora com os raios mais distantes do eixo óptico. (b) Para aberração comática, raios paralelos que não são paralelos ao eixo óptico são focados em diferentes alturas e distâncias focais, então a imagem contém uma “cauda” como um cometa (que é “coma” em latim). Observe que os raios coloridos servem apenas para facilitar a visualização; as cores não indicam a cor da luz.

Coma ou aberração comática

O coma é semelhante à aberração esférica, mas surge quando os raios de entrada não estão paralelos ao eixo óptico, conforme mostrado na Figura\(\PageIndex{8b}\). Lembre-se de que a aproximação de pequeno ângulo vale para espelhos esféricos que são pequenos em comparação com seu raio. Nesse caso, espelhos esféricos são boas aproximações dos espelhos parabólicos. Os espelhos parabólicos focalizam todos os raios que estão paralelos ao eixo óptico no ponto focal. No entanto, os raios paralelos que não são paralelos ao eixo óptico são focados em diferentes alturas e distâncias focais, conforme mostrado na Figura\(\PageIndex{8b}\). Como um espelho esférico é simétrico em relação ao eixo óptico, os vários raios coloridos nesta figura criam círculos da cor correspondente no plano focal.

Embora um espelho esférico seja mostrado na Figura\(\PageIndex{8b}\), a aberração comática ocorre também para espelhos parabólicos — ela não resulta de uma quebra na aproximação de pequeno ângulo (Equação\ ref {smallangle}). A aberração esférica, no entanto, ocorre apenas para espelhos esféricos e é resultado de uma quebra na aproximação de pequeno ângulo. Discutiremos o coma e a aberração esférica posteriormente neste capítulo, em conexão com telescópios.