30.9: O princípio de exclusão de Pauli
- Page ID
- 194166
Objetivos de
Ao final desta seção, você poderá:
- Defina a composição de um átomo junto com seus elétrons, nêutrons e prótons.
- Explique o princípio de exclusão de Pauli e sua aplicação ao átomo.
- Especifique os símbolos de shell e subshell e suas posições.
- Defina a posição dos elétrons em diferentes camadas de um átomo.
- Indique a posição de cada elemento na tabela periódica de acordo com o preenchimento do invólucro.
Átomos de múltiplos elétrons
Todos os átomos, exceto hidrogênio, são átomos de múltiplos elétrons. As propriedades físicas e químicas dos elementos estão diretamente relacionadas ao número de elétrons que um átomo neutro tem. A tabela periódica dos elementos agrupa elementos com propriedades semelhantes em colunas. Essa organização sistemática está relacionada ao número de elétrons em um átomo neutro, chamado número atômico,\(Z\). Veremos nesta seção que o princípio de exclusão é fundamental para as explicações subjacentes e que ele se aplica muito além do reino da física atômica.
Em 1925, o físico austríaco Wolfgang Pauli (veja a Figura) propôs a seguinte regra: Dois elétrons não podem ter o mesmo conjunto de números quânticos. Ou seja, dois elétrons não podem estar no mesmo estado. Essa afirmação é conhecida como princípio de exclusão de Pauli, porque exclui os elétrons de estarem no mesmo estado. O princípio de exclusão de Pauli é extremamente poderoso e amplamente aplicável. Ele se aplica a qualquer partícula idêntica com spin intrínseco meio integral - isto é, tendo\(s = 1/2, \, 3/2, . . .\) Portanto, dois elétrons não podem ter o mesmo conjunto de números quânticos.
Princípio de exclusão de Pa
Dois elétrons não podem ter o mesmo conjunto de números quânticos. Ou seja, dois elétrons não podem estar no mesmo estado.

Vamos examinar como o princípio de exclusão se aplica aos elétrons nos átomos. Os números quânticos envolvidos foram definidos em Números e Regras Quânticas como\(n, \, l, \, m_l, \, s\)\(m_s\) e. Como\(s\) é sempre\(1/2\) para elétrons, é redundante listar\(s\), então o omitimos e especificamos o estado de um elétron por um conjunto de quatro números\((n, \, l, \, m_l, \, m_s)\). Por exemplo, os números quânticos especificam\((2, \, 1, \, 0, - 1/2)\) completamente o estado de um elétron em um átomo.
Como dois elétrons não podem ter o mesmo conjunto de números quânticos, há limites para quantos deles podem estar no mesmo estado de energia. Observe que\(n\) determina o estado da energia na ausência de um campo magnético. Então\(n\), primeiro escolhemos e depois vemos quantos elétrons podem estar nesse estado de energia ou nível de energia. Considere o\(n = 1\) nível, por exemplo. O único valor que\(l\) pode ter é 0 (consulte [link] para obter uma lista de valores possíveis, uma vez que\(n\) seja conhecido) e, portanto, só\(m_l\) pode ser 0. A projeção de spin\(m_s\) pode ser\(+1/2\) ou\(-1/2\), portanto, pode haver dois elétrons no\(n = 1\) estado. Um tem números\((1,\space 0, \, 0, \, +1/2)\) quânticos e o outro tem\((1, \, 0, \, 0, \, -1/2)\). A figura ilustra que pode haver um ou dois elétrons tendo\(n = 1\), mas não três.
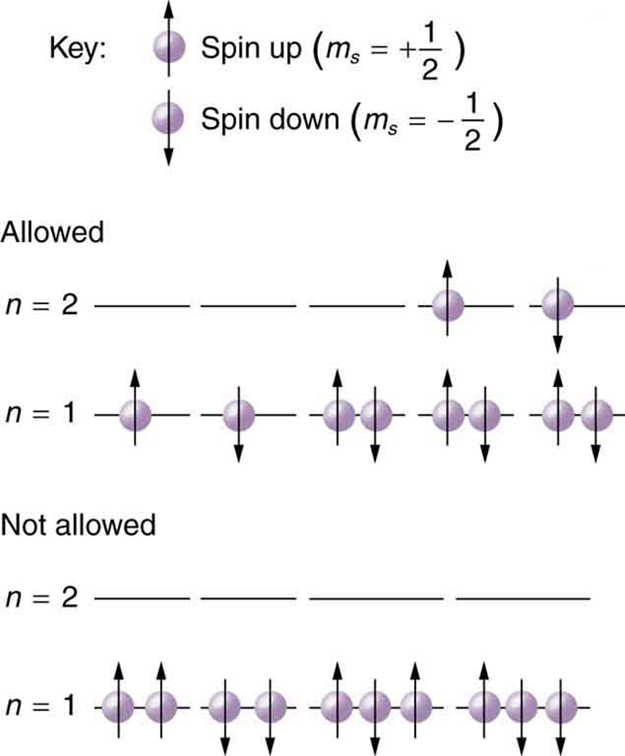
Conchas e subcamadas
Por causa do princípio de exclusão de Pauli, somente hidrogênio e hélio podem ter todos os seus elétrons no\(n = 1\) estado. O lítio (veja a tabela periódica) tem três elétrons e, portanto, é preciso estar no\(n = 2\) nível. Isso leva ao conceito de conchas e preenchimento de conchas. À medida que avançamos no número de elétrons, passamos do hidrogênio ao hélio, lítio, berílio, boro e assim por diante, e vemos que há limites para o número de elétrons para cada valor de\(n\). Valores mais altos da camada\(n\) correspondem a energias mais altas e podem permitir mais elétrons por causa das várias combinações de\(l, \, m_l\) e\(m_s\) isso é possível. Cada valor do número quântico principal corresponde\(n\), portanto, a uma camada atômica na qual um número limitado de elétrons pode entrar. As camadas e o número de elétrons nelas determinam as propriedades físicas e químicas dos átomos, pois são os elétrons mais externos que mais interagem com qualquer coisa fora do átomo.
As nuvens de probabilidade de elétrons com o menor valor de\(l\) estão mais próximas do núcleo e, portanto, mais estreitamente ligadas. Assim, quando as conchas se enchem, elas começam com\(l = 0\), progridem para\(l = 1\) e assim por diante. Cada valor de\(l\), portanto, corresponde a uma subcamada.
A tabela abaixo lista os símbolos tradicionalmente usados para denotar conchas e subcamadas.
| Concha | Subshell | Símbolo |
|---|---|---|
| \(n\) | \(l\) | |
| 1 | 0 | \(s\) |
| 2 | 1 | \(p\) |
| 3 | 2 | \(d\) |
| 4 | 3 | \(f\) |
| 5 | 4 | \(g\) |
| 6 | \(h\) | |
| \(6^i\) | \(i\) |
Para indicar conchas e subconchas, escrevemos\(nl\) com um número para\(n\) e uma letra para\(l\). Por exemplo, um elétron no\(n = 1\) estado deve ter\(l = 0\) e é indicado como um\(1s\) elétron. Dois elétrons no\(n = 1\) estado são indicados como\(1s^2\). Outro exemplo é um elétron no\(n = 2\) estado com\(l = 1\), escrito como\(2p\) .O caso de três elétrons com esses números quânticos está escrito\(2p^3\). Essa notação, chamada notação espectroscópica, é generalizada conforme mostrado na Figura.
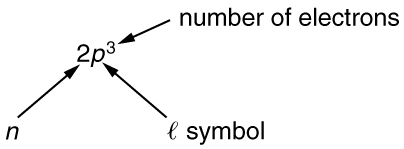
Contando o número de combinações possíveis de números quânticos permitidas pelo princípio de exclusão, podemos determinar quantos elétrons são necessários para preencher cada subcamada e camada.
Exemplo\(\PageIndex{1}\): How Many Electrons Can Be in This Shell?
Liste todos os conjuntos possíveis de números quânticos para a\(n = 2\) camada e determine o número de elétrons que podem estar na camada e em cada uma de suas subcamadas.
Estratégia
Dadas\(n = 2\) para o shell, as regras para números quânticos limitam\(l\) a ser 0 ou 1. A concha, portanto, tem duas subcamadas, rotuladas\(2s\)\(2p\) e. Como o\(l\) subshell mais baixo é preenchido primeiro, começamos com as possibilidades do\(2s\) subshell e depois prosseguimos com o\(2p\) subshell.
Solução
É conveniente listar os possíveis números quânticos em uma tabela, conforme mostrado abaixo.
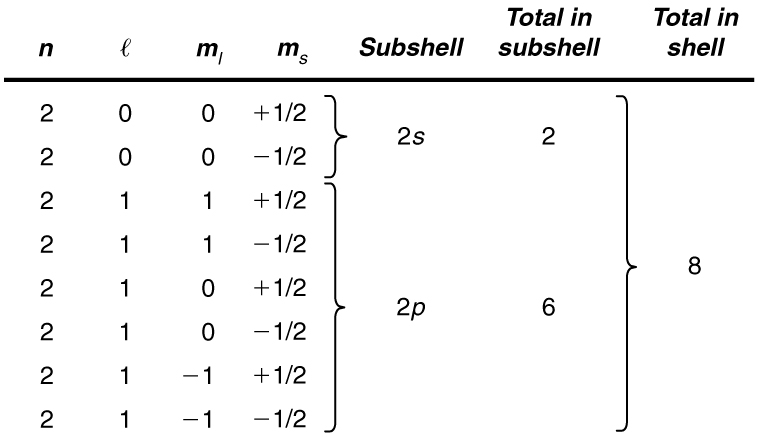
Discussão
É trabalhoso fazer uma tabela como essa toda vez que queremos saber quantos elétrons podem estar em uma camada ou subcamada. Existem regras gerais que são fáceis de aplicar, como veremos agora.
O número de elétrons que podem estar em uma subcamada depende inteiramente do valor de\(l\). Uma vez\(l\) conhecido, há um número fixo de valores de\(m_l\), cada um dos quais pode ter dois valores para\(m_s\). Primeiro, já que\(m_l\) vai de\(-l\) para\(l\) nas etapas de 1, existem\(2l + 1\) possibilidades. Esse número é multiplicado por 2, pois cada elétron pode ser girado para cima ou para baixo. Assim, o número máximo de elétrons que podem estar em uma subcamada é\(2(2l + 1)\).
Por exemplo, a\(2s\) subcamada em Example tem no máximo 2 elétrons nela, já que\(2(2l + 1) = 2(0 + 1) = 2\) para esta subcamada. Da mesma forma, a\(2p\) subcamada tem no máximo 6 elétrons, uma vez que\(2(2l + 1) = 2(2 + 1) = 6\). Para uma concha, o número máximo é a soma do que pode caber nas subcamadas. Algumas álgebras mostram que o número máximo de elétrons que podem estar em uma camada é\(2n^2\).
Por exemplo, para a primeira concha\(n = 1\), e assim por diante\(2n^2 = 2\). Já vimos que apenas dois elétrons podem estar na\(n = 1\) casca. Da mesma forma, para a segunda concha\(n = 2\), e assim por diante\(2n^2 = 8\). Conforme encontrado no exemplo, o número total de elétrons na\(n = 2\) camada é 8.
Exemplo\(\PageIndex{2}\): Subshells and Totals for \(n = 3\)
Quantas subcamadas estão na\(n = 3\) casca? Identifique cada subcamada, calcule o número máximo de elétrons que caberão em cada uma e verifique se o total é\(2n^2\).
Estratégia
As subcamadas são determinadas pelo valor de\(l\); assim, primeiro determinamos quais valores de\(l\) são permitidos e, em seguida, aplicamos a equação “número máximo de elétrons que podem estar em uma subcamada\(= 2(2l + 1)\)" para encontrar o número de elétrons em cada subcamada.
Solução
Pois\(n = 3\), sabemos que\(l\) pode ser\(0,\space 1\) ou\(2\), portanto, existem três subcamadas possíveis. Na notação padrão, eles são\(3s, \, 3p,\) rotulados como\(3d\) subcamadas e. Já vimos que 2 elétrons podem estar em um\(s\) estado e 6 em um\(p\) estado, mas vamos usar a equação “número máximo de elétrons que podem estar em uma subcamada\(= 2(2l + 1)\)" para calcular o número máximo em cada um:
\[3s \, has \, l = 0; \, thus, \, 2(2l + 1) = 2(0 + 1) = 2\]
\[3p \, has \, l = 1; \, thus, \, 2(2l + 1) = 2(2 + 1) = 6\]
\[3d \, has \, l = 2; \, thus, \, 2(2l + 1) = 2(4 + 1) = 10\]
\[Total = 18\]
\[(in \, the \, n = 3 \, shell)\]
A equação “número máximo de elétrons que podem estar em uma camada\(= 2n^2\)" fornece que o número máximo na\(n = 3\) camada seja
\[Maximum \, number \, of \, electrons = 2n^2 = 2(3)^2 = 2(9) = 18.\]
Discussão
O número total de elétrons nas três subcamadas possíveis é, portanto, o mesmo da fórmula\(2n^2\). Na notação padrão (espectroscópica), uma\(n = 3\) concha preenchida é indicada como\(3s^2 3p^6 3d^10\). As conchas não são preenchidas de forma simples. Antes que a\(n = 3\) casca esteja completamente preenchida, por exemplo, começamos a encontrar elétrons na\(n = 4\) casca.
Preenchimento da casca e tabela periódica
A tabela mostra as configurações de elétrons para os primeiros 20 elementos na tabela periódica, começando com hidrogênio e seu único elétron e terminando com cálcio. O princípio de exclusão de Pauli determina o número máximo de elétrons permitido em cada camada e subcamada. Mas a ordem na qual as camadas e subcamadas são preenchidas é complicada devido ao grande número de interações entre elétrons.
| Elemento | Número de elétrons (Z) | Configuração do estado fundamental |
|---|---|---|
| H | 1 | \(1s^1\) |
| Ele | 2 | \(1s^2\) |
| Li | 3 | \(1s^2 \, 2s^1\) |
| Seja | 4 | \( " \, 2s^2\) |
| B | 5 | \( " \, 2s^2 \, 2p^1\) |
| C | 6 | \( " \, 2s^2 \, 2p^2\) |
| N | 7 | \( " \, 2s^2 \, 2p^3\) |
| O | 8 | \( " \, 2s^2 \, 2p^4\) |
| F | 9 | \( " \, 2s^2 \, 2p^5\) |
| Ne | 10 | \( " \, 2s^2 \, 2p^6\) |
| Na | 11 | \( " \, 2s^2 \, 2p^6 \, 3s^1\) |
| Mg | 12 | \( " \, " \, " \, 3s^2\) |
| Al | 13 | \( " \, " \, " \, 3s^2 \, 3p^1\) |
| Si | 14 | \( " \, " \space" \, 3s^2 \, 3p^2\) |
| P | 15 | \( " \space " \, " \, 3s^2 \, 3p^3\) |
| S | 16 | \( " \, " \, " \, 3s^2 \, 3p^4\) |
| Cl | 17 | \( " \, " \, " \, 3s^2 \, 3p^5\) |
| Ar | 18 | \( " \, " \, " \, 3s^2 \, 3p^6\) |
| K | 19 | \( " \, " \, " \, 3s^2 \, 3p^6 \, 4s^1\) |
| Ca | 20 | \( " \, " \, " \, " \, " \, 4s^2\) |
Examinando a tabela acima, você pode ver que, à medida que o número de elétrons em um átomo aumenta de 1 em hidrogênio para 2 em hélio e assim por diante, a camada de menor energia é preenchida primeiro, ou seja, a\(n = 1\) camada se enche primeiro e depois a\(n = 2\) camada começa a se encher. Dentro de uma concha, as subcamadas são preenchidas começando pela mais baixa\(l\), ou com a\(s\) subcamada, depois a\(p\), e assim por diante, geralmente até que todas as subcamadas estejam preenchidas. A primeira exceção ocorre para o potássio, onde a\(4s\) subcamada começa a se encher antes que qualquer elétron entre na\(3d\) subcamada. A próxima exceção não é mostrada na Tabela; ela ocorre para o rubídio, onde a\(5s\) subcamada começa a se encher antes da\(4d\) subcamada. A razão para essas exceções é que\(l = 0\) os elétrons têm nuvens de probabilidade que penetram mais perto do núcleo e, portanto, estão mais estreitamente ligadas (com menor energia).
A figura mostra a tabela periódica dos elementos, através do elemento 118. De especial interesse são os elementos dos grupos principais, ou seja, aqueles nas colunas numeradas 1, 2, 13, 14, 15, 16, 17 e 18.
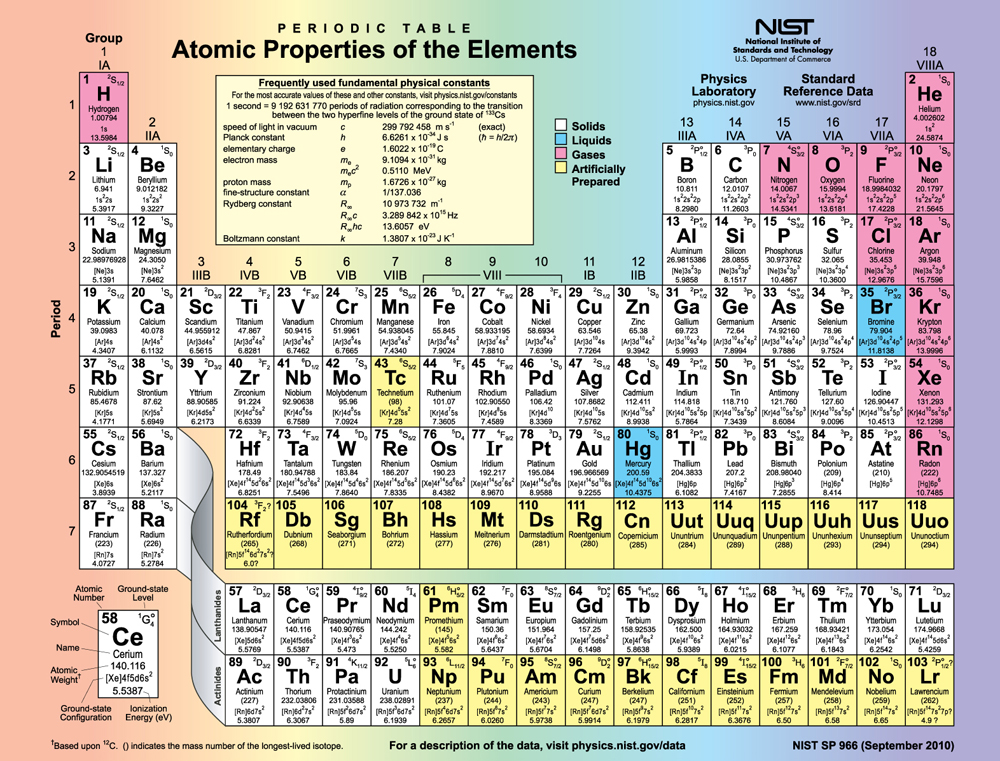
O número de elétrons na subcamada mais externa determina as propriedades químicas do átomo, pois são esses elétrons que estão mais distantes do núcleo e, portanto, interagem mais com outros átomos. Se a subcamada mais externa puder aceitar ou liberar um elétron facilmente, o átomo será altamente reativo quimicamente. Cada grupo na tabela periódica é caracterizado por sua configuração eletrônica mais externa. Talvez o mais conhecido seja o Grupo 18 (Grupo VIII), os gases nobres (hélio, néon, argônio, etc.). Esses gases são todos caracterizados por uma subcamada externa preenchida que é particularmente estável. Isso significa que eles têm grandes energias de ionização e não liberam prontamente um elétron. Além disso, se eles aceitassem um elétron extra, ele estaria em um nível significativamente mais alto e, portanto, frouxamente ligado. As reações químicas geralmente envolvem o compartilhamento de elétrons. Gases nobres podem ser forçados a se transformarem em compostos químicos instáveis somente sob alta pressão e temperatura.
O Grupo 17 (Grupo VII) contém os halogênios, como flúor, cloro, iodo e bromo, cada um com um elétron a menos do que um gás nobre vizinho. Cada halogênio tem 5\(p\) elétrons (uma\(p^5\) configuração), enquanto a\(p\) subcamada pode conter 6 elétrons. Isso significa que os halogênios têm uma vaga em sua subcamada mais externa. Assim, eles aceitam prontamente um elétron extra (ele se torna fortemente ligado, fechando a camada como nos gases nobres) e são altamente reativos quimicamente. Também é provável que os halogênios formem íons negativos isolados, como\(Cl^-\) encaixar um elétron extra na vaga na subcamada externa. Em contraste, metais alcalinos, como sódio e potássio, todos têm um único\(s\) elétron em sua subcamada mais externa (uma\(s^1\) configuração) e são membros do Grupo 1 (Grupo I). Esses elementos liberam facilmente seu elétron extra e, portanto, são altamente reativos quimicamente. Como você pode esperar, eles também tendem a formar íons positivos isoladamente, como\(Na^+\), ao perder seu elétron externo frouxamente ligado. Eles são metais (condutores), porque o elétron externo frouxamente ligado pode se mover livremente.
É claro que outros grupos também são interessantes. Carbono, silício e germânio, por exemplo, têm produtos químicos semelhantes e estão no Grupo 4 (Grupo IV). O carbono, em particular, é extraordinário em sua capacidade de formar muitos tipos de ligações e fazer parte de cadeias longas, como moléculas inorgânicas. O grande grupo dos chamados elementos de transição é caracterizado pelo preenchimento das\(d\) subcamadas e pelo cruzamento dos níveis de energia. Grupos mais pesados, como a série dos lantanídeos, são mais complexos — suas conchas não são preenchidas em uma ordem simples. Mas os grupos reconhecidos por químicos como Mendeleev têm uma explicação na subestrutura dos átomos.
EXPLORAÇÕES DE PHET: CONSTRUA UM ÁTOMO
Construa um átomo a partir de prótons, nêutrons e elétrons e veja como o elemento, a carga e a massa mudam. Em seguida, jogue um jogo para testar suas ideias!

Resumo
- O estado de um sistema é completamente descrito por um conjunto completo de números quânticos. Este conjunto é escrito como\((n, \, l, \, m_i, \, m_s)\).
- O princípio de exclusão de Pauli diz que dois elétrons não podem ter o mesmo conjunto de números quânticos; ou seja, dois elétrons não podem estar no mesmo estado.
- Essa exclusão limita o número de elétrons nas camadas e subcamadas atômicas. Cada valor de\(n\) corresponde a um shell, e cada valor de\(l\) corresponde a um subshell.
- O número máximo de elétrons que podem estar em uma subcamada é\(2(2l + 1)\).
- O número máximo de elétrons que podem estar em uma camada é\(2n^2\).
Notas de pé
- 1 É incomum lidar com subcamadas com\(l\) mais de 6, mas quando encontradas, elas continuam sendo rotuladas em ordem alfabética.
Glossário
- número atômico
- o número de prótons no núcleo de um átomo
- princípio de exclusão de Pauli
- um princípio que afirma que dois elétrons não podem ter o mesmo conjunto de números quânticos; ou seja, dois elétrons não podem estar no mesmo estado
- concha
- uma nuvem de probabilidade para elétrons que tem um único número quântico principal
- subconcha
- a nuvem de probabilidade para elétrons que tem um único número quântico de momento angular


