30.E: Física Atômica (Exercícios)
- Page ID
- 194137
Perguntas conceituais
30.1: Descoberta do Átomo
1. Cite três tipos diferentes de evidências da existência de átomos.
2. Explique por que os padrões observados na tabela periódica dos elementos são evidências da existência de átomos e por que o movimento browniano é um tipo mais direto de evidência de sua existência.
3. Se os átomos existem, por que não podemos vê-los com luz visível?
30.2: Descoberta das partes do átomo: elétrons e núcleos
4. Quais são as duas evidências que permitiram o primeiro cálculo de mim, a massa do elétron? Justifique sua resposta.
(a) As proporções\(\displaystyle q_e/m_e\)\(\displaystyle q_p/m_p\) e.
(b) Os valores de\(\displaystyle q_e\)\(\displaystyle E_B\) e.
(c) A proporção\(\displaystyle q_e/m_e\)\(\displaystyle q_e\) e.
5. Como as órbitas permitidas para elétrons em átomos diferem das órbitas permitidas para planetas ao redor do sol? Explique aqui como o princípio da correspondência se aplica.
30.3: Teoria do Átomo de Hidrogênio de Bohr
6. Como as órbitas permitidas para elétrons em átomos diferem das órbitas permitidas para planetas ao redor do sol? Explique aqui como o princípio da correspondência se aplica.
7. Explique como a regra de Bohr para a quantização do momento angular orbital de elétrons difere da regra real.
8. O que é um átomo semelhante ao hidrogênio e como as energias e os raios de suas órbitas de elétrons estão relacionados aos do hidrogênio?
30.4: Raios X - Origens e aplicações atômicas
9. Explique por que os raios X característicos são os mais energéticos no espectro de emissão EM de um determinado elemento.
10. Por que a energia dos raios X característicos se torna cada vez maior para átomos mais pesados?
11. Observadores a uma distância segura de um teste atmosférico de uma bomba nuclear sentem seu calor, mas não recebem nenhum de seus abundantes raios X. Por que o ar é opaco aos raios X, mas transparente ao infravermelho?
12. Os lasers são usados para gravar e ler CDs. Explique por que um laser que emite luz azul seria capaz de queimar e ler mais informações do que um que emite infravermelho.
13. As redes cristalinas podem ser examinadas com raios x, mas não com UV. Por quê?
14. Os tomógrafos não detectam detalhes menores que cerca de 0,5 mm. Essa limitação se deve ao comprimento de onda dos raios X? Explique.
30.5: Aplicações de excitações e desexcitações atômicas
15. Como as órbitas permitidas para elétrons em átomos diferem das órbitas permitidas para planetas ao redor do sol? Explique aqui como o princípio da correspondência se aplica.
16. Os espectros atômicos e moleculares são discretos. O que significa discreto e como os espectros discretos estão relacionados à quantização de órbitas de energia e elétrons em átomos e moléculas?
17. O gás hidrogênio só pode absorver radiação EM que tenha uma energia correspondente a uma transição no átomo, assim como ele só pode emitir essas energias discretas. Quando um espectro é obtido da coroa solar, no qual uma ampla faixa de comprimentos de onda EM passa por um gás hidrogênio muito quente, o espectro de absorção mostra todas as características do espectro de emissão. Mas quando essa radiação EM passa pelo gás hidrogênio à temperatura ambiente, somente a série Lyman é absorvida. Explique a diferença.
18. Os lasers são usados para gravar e ler CDs. Explique por que um laser que emite luz azul seria capaz de queimar e ler mais informações do que um que emite infravermelho.
19. O revestimento interno dos tubos de luz fluorescente absorve a luz ultravioleta e, posteriormente, emite luz visível. Um inventor afirma que ele é capaz de fazer o processo inverso. A afirmação do inventor é possível?
20. Qual é a diferença entre fluorescência e fosforescência?
21. Como você pode dizer que um holograma é uma verdadeira imagem tridimensional e que aqueles em filmes 3D não são?
30.6: A natureza ondulatória da matéria causa quantização
22. Como o comprimento de onda de Broglie dos elétrons está relacionado à quantização de suas órbitas em átomos e moléculas?
30.7: Padrões em espectros revelam mais quantização
23. O que é o efeito Zeeman e que tipo de quantização foi descoberto por causa desse efeito?
30.8: Números e regras quânticas
24. Defina os números quânticos\(\displaystyle n, l,m_l, s\),\(\displaystyle m_s\) e.
25. Para um determinado valor de\(\displaystyle n\), quais são os valores permitidos de\(\displaystyle l\)?
26. Para um determinado valor de\(\displaystyle l\), quais são os valores permitidos de\(\displaystyle m_l\)? Quais são os valores permitidos\(\displaystyle m_l\) para um determinado valor de\(\displaystyle n\)? Dê um exemplo em cada caso.
27. Liste todos os valores possíveis de\(\displaystyle s\) e\(\displaystyle m_s\) para um elétron. Existem partículas para as quais esses valores são diferentes? O mesmo?
30.9: O princípio de exclusão de Pauli
28. Identifique a camada, a subcamada e o número de elétrons para o seguinte:
(uma)\(\displaystyle 2p^3\).
(b)\(\displaystyle 4d^9\).
(c)\(\displaystyle 3s^1\).
(d)\(\displaystyle 5g^{16}\).
29. Quais das seguintes opções não são permitidas? Indique qual regra é violada para qualquer regra que não seja permitida.
(uma)\(\displaystyle 1p^3\)
(b)\(\displaystyle 2p^8\)
(c)\(\displaystyle 3g^{11}\)
(d)\(\displaystyle 4f^2\)
Problemas e exercícios
30.1: Descoberta do Átomo
30. Usando as proporções carga/massa fornecidas para elétrons e prótons, e sabendo que as magnitudes de suas cargas são iguais, qual é a razão entre a massa do próton e a do elétron? (Observe que, como as relações carga/massa são fornecidas com precisão de apenas três dígitos, sua resposta pode ser diferente da proporção aceita no quarto dígito.)
Solução
\(\displaystyle 1.84×10^3\)
31. (a) Calcule a massa de um próton usando a relação carga/massa fornecida para ele neste capítulo e sua carga conhecida.
(b) Como seu resultado se compara com a massa de prótons dada neste capítulo?
32. Se alguém quisesse construir um modelo em escala do átomo com um núcleo de 1,00 m de diâmetro, a que distância precisaria estar o elétron mais próximo?
Solução
50 km
30.2: Descoberta das partes do átomo: elétrons e núcleos
33. Rutherford descobriu que o tamanho do núcleo era de cerca de 10 a 15m. Isso implicava uma enorme densidade. Qual seria essa densidade para o ouro?
Solução
\(\displaystyle 6×10^{20}kg/m^3\)
34. No experimento de gotas de óleo de Millikan, observa-se uma pequena gota de óleo mantida imóvel entre duas placas. Considere que a tensão entre as placas seja de 2033 V e a separação da placa seja de 2,00 cm. A gota de óleo (de densidade\(\displaystyle 0.81 g/cm^3\)) tem um diâmetro de\(\displaystyle 4.0×10^{−6}m\). Encontre a carga na gota, em termos de unidades de elétrons.
35. (a) Uma aspirante a física quer construir um modelo em escala de um átomo de hidrogênio para seu projeto de feira de ciências. Se o átomo tem 1,00 m de diâmetro, qual o tamanho que ela deveria tentar fazer com o núcleo?
(b) Quão fácil será fazer isso?
Solução
(a)\(\displaystyle 10.0 μm\)
(b) Não é difícil fazer uma com aproximadamente esse tamanho. Seria mais difícil fazer com que fosse exatamente 10,0 μm.
30.3: Teoria do Átomo de Hidrogênio de Bohr
36. Ao calcular seu comprimento de onda, mostre que a primeira linha da série Lyman é a radiação UV.
Solução
\(\displaystyle \frac{1}{λ}=R(\frac{1}{n^2_f}−\frac{1}{n^2_i})⇒λ=\frac{1}{R}[\frac{(n_i⋅n_f)^2}{n^2_i−n^2_f}];n_i=2,n_f=1,\) para isso
\(\displaystyle λ=(\frac{m}{1.097×10^7})[\frac{(2×1)^2}{2^2−1^2}]=1.22×10^{−7}m=122 nm\), que é radiação UV.
37. Encontre o comprimento de onda da terceira linha na série Lyman e identifique o tipo de radiação EM.
38. Pesquise os valores das quantidades em\(\displaystyle a_B=\frac{h^2}{4π^2m_ekq^2_e}\) e verifique se o raio de Bohr\(\displaystyle a_B\) é\(\displaystyle 0.529×10^{−10}m\).
Solução
\(\displaystyle a_B=\frac{h^2}{4π^2mekZq^2_e}=\frac{(6.626×10^{−34}J⋅s)^2}{4π^2(9.109×10^{−31}kg)(8.988×10^9N⋅m^2/C^2)(1)(1.602×10^{−19}C)^2}=0.529×10^{−10}m\)
39. Verifique se a energia do estado fundamental\(\displaystyle E_0\) é 13,6 eV usando\(\displaystyle E0=\frac{2π^2q^4_em_ek^2}{h^2}\).
40. Se um átomo de hidrogênio tem seu elétron no\(\displaystyle n=4\) estado, quanta energia em eV é necessária para ionizá-lo?
Solução
0,850 eV
41. Um átomo de hidrogênio em estado excitado pode ser ionizado com menos energia do que quando está em seu estado fundamental. O que é n para um átomo de hidrogênio se 0,850 eV de energia pode ionizá-lo?
42. Encontre o raio de um átomo de hidrogênio no\(\displaystyle n=2\) estado de acordo com a teoria de Bohr.
Solução
\(\displaystyle 2.12×10^{–10}m\)
43. Mostre isso\(\displaystyle (13.6 eV)/hc=1.097×10^7m=R\) (a constante de Rydberg), conforme discutido no texto.
44. Qual é a linha de menor comprimento de onda da série Balmer? Está na parte visível do espectro?
Solução
365 nm
Está no ultravioleta.
45. Mostre que toda a série Paschen está na parte infravermelha do espectro. Para fazer isso, você só precisa calcular o menor comprimento de onda da série.
46. As séries Balmer e Lyman se sobrepõem? Para responder a isso, calcule a linha Balmer de menor comprimento de onda e a linha Lyman de maior comprimento de onda.
Solução
: Sem sobreposição:
365 nm
(122 nm)
47. (a) Qual linha da série Balmer é a primeira na parte UV do espectro?
(b) Quantas linhas da série Balmer estão na parte visível do espectro?
(c) Quantos estão no UV?
48. Um comprimento de onda de\(\displaystyle 4.653 μm\) é observado em um espectro de hidrogênio para uma transição que termina no\(\displaystyle n_f=5\) nível. Qual era\(\displaystyle n_i\) o nível inicial do elétron?
Solução
7
49. Um íon de hélio ionizado isoladamente tem apenas um elétron e é indicado\(\displaystyle He^+\). Qual é o raio do íon no estado fundamental em comparação com o raio de Bohr do átomo de hidrogênio?
50. Um íon berílio com um único elétron (indicado\(\displaystyle Be^{3+}\)) está em um estado excitado com raio igual ao do estado fundamental do hidrogênio.
(a) O que é\(\displaystyle n\) para o\(\displaystyle Be^{3+}\) íon?
(b) Quanta energia em eV é necessária para ionizar o íon desse estado excitado?
Solução
(a) 2
(b) 54,4 eV
51. Os átomos podem ser ionizados por colisões térmicas, como nas altas temperaturas encontradas na coroa solar. Um desses íons é\(\displaystyle C^{+5}\) um átomo de carbono com apenas um único elétron.
(a) Por qual fator as energias de seus níveis semelhantes ao hidrogênio são maiores do que as do hidrogênio?
(b) Qual é o comprimento de onda da primeira linha da série Paschen deste íon?
(c) Que tipo de radiação EM é essa?
52. Verifique as equações\(\displaystyle r_n=\frac{n^2}{Z}a_B\) e\(\displaystyle a_B=\frac{h^2}{4π^2m_ekq^2_e}=0.529×10^{−10}m\) use a abordagem indicada no texto. Ou seja, iguale as forças de Coulomb e centrípeta e, em seguida, insira uma expressão para velocidade a partir da condição de quantização do momento angular.
Solução
\(\displaystyle \frac{kZq^2_e}{r^2_n}=\frac{m_eV^2}{r_n}\), para que\(\displaystyle r_n=\frac{kZq^2_e}{m_eV^2}=\frac{kZq^2_e}{m_e}\frac{1}{V^2}\). A partir da equação\(\displaystyle m_evr_n=n\frac{h}{2π}\), podemos substituir a velocidade, dando: de\(\displaystyle r_n=\frac{kZq^2_e}{m_e}⋅\frac{4π^2m^2_er^2_n}{n^2h^2}\) modo que\(\displaystyle r_n=\frac{n^2}{Z}\frac{h^2}{4π^2m_ekq^2_e}=\frac{n^2}{Z}a_B\), onde\(\displaystyle a_B=\frac{h^2}{4π^2m_ekq^2_e}\).
53. O comprimento de onda das quatro linhas da série Balmer para hidrogênio é de 410,3, 434,2, 486,3 e 656,5 nm. Qual diferença percentual média é encontrada entre esses números de comprimento de onda e aqueles previstos por\(\displaystyle \frac{1}{λ}=R(\frac{1}{n^2_f}−\frac{1}{n^2+i})\)? É incrível como uma fórmula simples (desconectada originalmente da teoria) poderia duplicar esse fenômeno.
30.4: Raios X - Origens e aplicações atômicas
54. (a) Qual é a radiação de raio-x de menor comprimento de onda que pode ser gerada em um tubo de raios X com uma tensão aplicada de 50,0 kV?
(b) Calcule a energia do fóton em eV.
(c) Explique a relação da energia do fóton com a tensão aplicada.
Solução
(a)\(\displaystyle 0.248×10^{−10}m\)
(b) 50,0 keV
(c) A energia do fóton é simplesmente a tensão aplicada vezes a carga do elétron, então o valor da tensão em volts é o mesmo que o valor da energia em elétron-volts.
55. Um tubo de televisão colorido também gera alguns raios X quando seu feixe de elétrons atinge a tela. Qual é o menor comprimento de onda desses raios X, se um potencial de 30,0 kV for usado para acelerar os elétrons? (Observe que as TVs têm blindagem para evitar que esses raios X exponham os espectadores.)
56. Um tubo de raios X tem uma tensão aplicada de 100 kV.
(a) Qual é o fóton de raio-x mais energético que ele pode produzir? Expresse sua resposta em elétron-volts e joules.
(b) Encontre o comprimento de onda desse raio-X.
Solução
(a)\(\displaystyle 100×10^3eV, 1.60×10^{−14}J\)
(b)\(\displaystyle 0.124×10^{−10}m\)
57. A energia máxima característica do fóton de raios-X vem da captura de um elétron livre em uma vaga de\(\displaystyle K\) camada. O que é essa energia de fótons em keV para tungstênio, supondo que o elétron livre não tenha energia cinética inicial?
58. Quais são as energias aproximadas dos raios\(\displaystyle K_β\) X\(\displaystyle K_α\) e X do cobre?
Solução
(a) 8,00 keV
(b) 9,48 keV
30.5: Aplicações de excitações e desexcitações atômicas
59. A figura mostra o diagrama do nível de energia do néon.
(a) Verifique se a energia do fóton emitido quando o néon passa de seu estado metaestável para o imediatamente abaixo é igual a 1,96 eV.
(b) Mostre que o comprimento de onda dessa radiação é de 633 nm.
(c) Qual comprimento de onda é emitido quando o néon faz uma transição direta para seu estado fundamental?
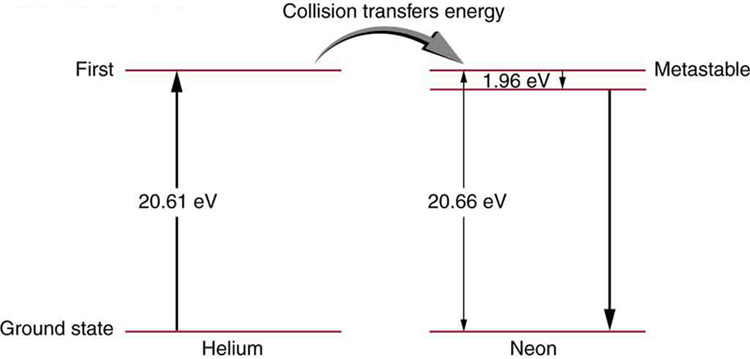
Solução
(a) 1,96 eV
(b)\(\displaystyle (1240 eV⋅nm)/(1.96 eV)=633 nm\)
(c) 60,0 nm
60. Um laser de hélio-néon é bombeado por descarga elétrica. Qual radiação eletromagnética de comprimento de onda seria necessária para bombeá-la? Consulte a Figura para obter informações sobre o nível de energia.
61. Os lasers de rubi têm átomos de cromo dopados em um cristal de óxido de alumínio. O diagrama do nível de energia do cromo em um rubi é mostrado na Figura. Qual comprimento de onda é emitido por um laser de rubi?

Os átomos de cromo em um cristal de óxido de alumínio têm esses níveis de energia, um dos quais é metaestável. Essa é a base de um laser de rubi. A luz visível pode bombear o átomo para um estado excitado acima do estado metaestável para atingir uma inversão populacional.
Solução
693 nm
62. (a) Quais fótons de energia podem bombear átomos de cromo em um laser de rubi do estado fundamental para seu segundo e terceiro estados excitados?
(b) Quais são os comprimentos de onda desses fótons? Verifique se eles estão na parte visível do espectro.
63. Alguns dos lasers mais poderosos são baseados nos níveis de energia do neodímio em sólidos, como o vidro, conforme mostrado na Figura.
(a) Qual luz de comprimento de onda médio pode bombear o neodímio para níveis acima de seu estado metaestável?
(b) Verifique se a transição de 1,17 eV produz\(\displaystyle 1.06 μm\) radiação.
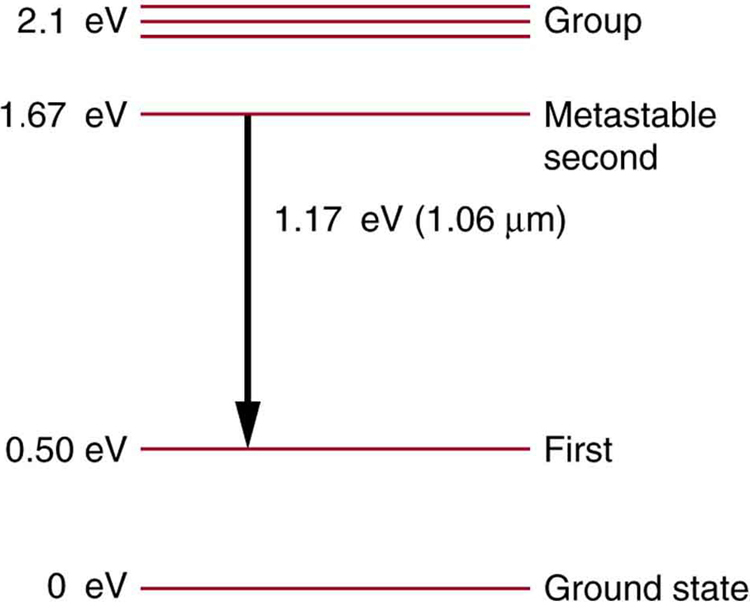
Os átomos de neodímio no vidro têm esses níveis de energia, um dos quais é metaestável. O grupo de níveis acima do estado metaestável é conveniente para alcançar uma inversão populacional, uma vez que fótons de muitas energias diferentes podem ser absorvidos por átomos no estado fundamental.
Solução
(a) 590 nm
(b)\(\displaystyle (1240 eV⋅nm)/(1.17 eV)=1.06 μm\)
30.8: Números e regras quânticas
64. Se um átomo tem um elétron no\(\displaystyle n=5\) estado com\(\displaystyle m_l=3\), quais são os valores possíveis de\(\displaystyle l\)?
A solução
\(\displaystyle l=4, 3\) é possível desde\(\displaystyle l<n\)\(\displaystyle ∣m_l∣≤l\) e.
65. Um átomo tem um elétron com\(\displaystyle m_l=2\). Qual é o menor valor desse\(\displaystyle n\) elétron?
66. Quais são os valores possíveis\(\displaystyle m_l\) de um elétron no\(\displaystyle n=4\) estado?
A solução
\(\displaystyle n=4⇒l=3, 2, 1, 0⇒m_l=±3,±2,±1, 0\) é possível.
67. Quais restrições, se houver,\(\displaystyle m_l=1\) colocam um valor nos outros números quânticos de um elétron em um átomo?
68. (a) Calcule a magnitude do momento angular de um\(\displaystyle l=1\) elétron.
(b) Compare sua resposta com o valor proposto por Bohr para o\(\displaystyle n=1\) estado.
Solução
(a)\(\displaystyle 1.49×10^{−34}J⋅s\)
(b)\(\displaystyle 1.06×10^{−34}J⋅s\)
69. (a) Qual é a magnitude do momento angular de um\(\displaystyle l=1\) elétron?
(b) Calcule a magnitude do momento angular de rotação do elétron.
(c) Qual é a proporção desses momentos angulares?
70. Repita o exercício para\(\displaystyle l=3\).
Solução
(a)\(\displaystyle 3.66×10^{−34}J⋅s\)
(b)\(\displaystyle s=9.13×10^{−35}J⋅s\)
(c)\(\displaystyle \frac{L}{S}=\frac{\sqrt{12}}{\sqrt{3/4}}=4\)
71. (a) Quantos ângulos posso\(\displaystyle L\) fazer com o eixo z de um\(\displaystyle l=2\) elétron?
(b) Calcule o valor do menor ângulo.
72. Quais ângulos o spin\(\displaystyle S\) de um elétron pode fazer com o eixo z?
Solução
\(\displaystyle θ=54.7º, 125.3º\)
30.9: O princípio de exclusão de Pauli
73. (a) Quantos elétrons podem estar na\(\displaystyle n=4\) casca?
(b) Quais são suas subcamadas e quantos elétrons podem estar em cada uma?
Solução
(a) 32.
(b)\(\displaystyle 2\) em\(\displaystyle s\),\(\displaystyle 6\) em\(\displaystyle p\)\(\displaystyle d\),\(\displaystyle 10\) em e 14 em\(\displaystyle f\), para um total de 32.
74. (a) Qual é o valor mínimo de 1 para uma subcamada que tem 11 elétrons nela?
(b) Se essa subcamada estiver na\(\displaystyle n=5\) casca, qual é a notação espectroscópica desse átomo?
75. (a) Se uma subcamada de um átomo tem 9 elétrons nela, qual é o valor mínimo de\(\displaystyle l\)?
(b) Qual é a notação espectroscópica desse átomo, se essa subcamada fizer parte da\(\displaystyle n=3\) concha?
Solução
(a) 2
(b)\(\displaystyle 3d^9\)
76. (a) Liste todos os conjuntos possíveis de números quânticos\(\displaystyle (n,l,m_l,m_s)\) para a\(\displaystyle n=3\) camada e determine o número de elétrons que podem estar na camada e em cada uma de suas subcamadas.
(b) Mostre que o número de elétrons na camada é igual\(\displaystyle 2n^2\) e que o número em cada subcamada é\(\displaystyle 2(2l+1)\).
77. Quais das seguintes notações espectroscópicas não são permitidas? Indique qual regra é violada para cada uma que não é permitida.
(uma)\(\displaystyle 5s^1\)
(b)\(\displaystyle 1d^1\)
(c)\(\displaystyle 4s^3\)
(d)\(\displaystyle 3p^7\)
(e)\(\displaystyle 5g^{15}\).
A solução
(b)\(\displaystyle n≥l\) é violada,
(c) não pode ter 3 elétrons na\(\displaystyle s\) subcamada, pois\(\displaystyle 3>(2l+1)=2\)
(d) não pode ter 7 elétrons na\(\displaystyle p\) subcamada desde\(\displaystyle 7>(2l+1)=2(2+1)=6\)
78. Quais das seguintes notações espectroscópicas são permitidas (ou seja, que não violam nenhuma das regras relativas aos valores dos números quânticos)?
(uma)\(\displaystyle 1s^1\)
(b)\(\displaystyle 1d^3\)
(c)\(\displaystyle 4s^2\)
(d)\(\displaystyle 3p^7\)
(e)\(\displaystyle 6h^{20}\)
79. (a) Usando o princípio de exclusão de Pauli e as regras que relacionam os valores permitidos dos números quânticos\(\displaystyle (n,l,m_l,m_s)\), prove que o número máximo de elétrons em uma subcamada é\(\displaystyle 2n^2\).
(b) De maneira semelhante, prove que o número máximo de elétrons em uma camada é\(\displaystyle 2n^2\).
Solução
(a) O número de valores diferentes de\(\displaystyle m_l\) é\(\displaystyle ±l,±(l−1),...,0\) para cada um\(\displaystyle l>0\) e um para\(\displaystyle l=0⇒(2l+1)\). Também é um fator geral de 2, pois cada um\(\displaystyle m_l\) pode ser\(\displaystyle m_s\) igual a\(\displaystyle +1/2\) ou\(\displaystyle −1/2⇒2(2l+1)\).
(b) para cada valor de\(\displaystyle l\), você\(\displaystyle 2(2l+1)=0, 1, 2, ...,(n–1)⇒2{[(2)(0)+1]+[(2)(1)+1]+....+[(2)(n−1)+1]}=2[1+3+...+(2n−3)+(2n−1)]\) vê que a expressão na caixa é\(\displaystyle =n^2\), imagine tirar\(\displaystyle (n−1)\) do último termo e adicioná-lo ao primeiro termo\(\displaystyle =2[1+(n–1)+3+...+(2n−3)+(2n−1)–(n−1)]=2[n+3+....+(2n−3)+n]\). Agora,\(\displaystyle (n−3)\) tire do penúltimo termo e acrescente ao segundo termo\(\displaystyle 2[n+n+...+n+n]=2n^2\).
80. Conceitos integrados
Estime a densidade de um núcleo calculando a densidade de um próton, considerando-o uma esfera de 1,2 fm de diâmetro. Compare seu resultado com o valor estimado neste capítulo.
81. Conceitos integrados
Supõe-se que as forças elétricas e magnéticas em um elétron no CRT em [link] estejam em direções opostas. Verifique isso determinando a direção de cada força para a situação mostrada. Explique como você obtém as instruções (ou seja, identifique as regras usadas).
Solução
A força elétrica no elétron está para cima (em direção à placa carregada positivamente). A força magnética está baixa (pela RHR).
82. (a) Qual é a distância entre as fendas de uma grade de difração que produz um máximo de primeira ordem para a primeira linha de Balmer em um ângulo de\(\displaystyle 20.0º\)?
(b) Em que ângulo a quarta linha da série Balmer aparecerá em primeira ordem?
(c) Em que ângulo será o máximo de segunda ordem para a primeira linha?
83. Conceitos integrados
Uma galáxia se afastando da Terra tem uma velocidade de\(\displaystyle 0.0100c\). Que comprimento de onda observamos para uma\(\displaystyle n_f=2\) transição\(\displaystyle n_i=7\) para hidrogênio nessa galáxia?
Solução
401 nm
84. Conceitos integrados
Calcule a velocidade de uma estrela se movendo em relação à Terra se você observar um comprimento de onda de 91,0 nm para hidrogênio ionizado capturando um elétron diretamente no orbital mais baixo (ou seja\(\displaystyle n_f=1\), uma transição\(\displaystyle n_i=∞\) para ou série Lyman).
85. Conceitos integrados
Em um experimento de gota de óleo Millikan usando uma configuração como a de [link], uma diferença de potencial de 500 V é aplicada a placas separadas por 2,50 cm.
(a) Qual é a massa de uma gota de óleo com dois elétrons extras suspensos imóveis pelo campo entre as placas?
(b) Qual é o diâmetro da gota, supondo que seja uma esfera com a densidade do azeite?
Solução
(a)\(\displaystyle 6.54×10^{−16}kg\)
(b)\(\displaystyle 5.54×10^{−7}m\)
86. Conceitos integrados
Qual separação de dupla fenda produziria um máximo de primeira ordem\(\displaystyle 3.00º\) para raios x de 25,0 keV? A pequena resposta indica que o caráter ondulatório dos raios X é melhor determinado fazendo com que eles interajam com objetos muito pequenos, como átomos e moléculas.
87. Conceitos integrados
Em um experimento de laboratório projetado para duplicar a determinação de Thomson de\(\displaystyle q_e/m_e\), um feixe de elétrons com uma velocidade de\(\displaystyle 6.00×10^7m/s\) entra em um campo\(\displaystyle 5.00×10^{−3}T\) magnético. O feixe se move perpendicularmente ao campo em um caminho com um raio de curvatura de 6,80 cm. Determine\(\displaystyle q_e/m_e\) a partir dessas observações e compare o resultado com o valor conhecido.
Solução
\(\displaystyle 1.76×10^{11}C/kg\), que concorda com o valor conhecido de\(\displaystyle 1.759×10^{11}C/kg\) até dentro da precisão da medição
88. Conceitos integrados
Encontre o valor de\(\displaystyle l\), o número quântico do momento angular orbital, para a lua ao redor da Terra. O valor extremamente grande obtido implica que é impossível dizer a diferença entre órbitas quantizadas adjacentes para objetos macroscópicos.
89. Conceitos integrados
Partículas chamadas múons existem em raios cósmicos e podem ser criadas em aceleradores de partículas. Os múons são muito parecidos com os elétrons, com a mesma carga e rotação, mas têm uma massa 207 vezes maior. Quando os múons são capturados por um átomo, eles orbitam exatamente como um elétron, mas com um raio menor, já que a massa em\(\displaystyle a_B=\frac{h^2}{4π^2m_ekq^2_e}=0.529×10^{−10}m\) é\(\displaystyle 207 m_e\).
(a) Calcule o raio da\(\displaystyle n=1\) órbita de um múon em um íon de urânio\(\displaystyle (Z=92)\).
(b) Compare isso com o raio de 7,5 fm de um núcleo de urânio. Observe que, como o múon orbita dentro do elétron, ele cai em uma órbita semelhante ao hidrogênio. Como sua resposta é menor que o raio do núcleo, você pode ver que os fótons emitidos quando o múon cai em sua órbita mais baixa podem fornecer informações sobre o núcleo.
Solução
(a) 2,78 fm
(b) 0,37 do raio nuclear.
90. Conceitos integrados
Calcule a quantidade mínima de energia em joules necessária para criar uma inversão populacional em um laser de hélio-néon contendo\(\displaystyle 1.00×10^{−4}\) toupeiras de néon.
91. Conceitos integrados
Um laser de dióxido de carbono usado em cirurgia emite radiação infravermelha com um comprimento de onda de\(\displaystyle 10.6 μm\). Em 1,00 ms, esse laser elevou a temperatura\(\displaystyle 1.00 cm^3\) da carne\(\displaystyle 100ºC\) e a evaporou.
(a) Quantos fótons foram necessários? Você pode presumir que a carne tem o mesmo calor de vaporização da água.
(b) Qual foi a potência mínima de saída durante o flash?
Solução
(a)\(\displaystyle 1.34×10^{23}\)
(b) 2,52 MW
92. Conceitos integrados
Suponha que um scanner de ressonância magnética use ondas de rádio de 100 MHz
(a) Calcule a energia do fóton.
(b) Como isso se compara às energias de ligação molecular típicas?
93. Conceitos integrados
(a) Um laser excimer usado para correção da visão emite UV de 193 nm. Calcule a energia do fóton em eV.
(b) Esses fótons são usados para evaporar o tecido da córnea, que é muito semelhante à água em suas propriedades. Calcule a quantidade de energia necessária por molécula de água para fazer a mudança de fase de líquido para gás. Ou seja, divida o calor da vaporização em kJ/kg pelo número de moléculas de água em um quilograma.
(c) Converta isso em eV e compare com a energia do fóton. Discuta as implicações.
Solução
(a) 6,42 eV
(b)\(\displaystyle 7.27×10^{−20}J/molecule\)
(c) 0,454 eV, 14,1 vezes menor que um único fóton UV. Portanto, cada fóton evaporará aproximadamente 14 moléculas de tecido. Isso dá ao cirurgião um método bastante preciso de remover o tecido corneano da superfície do olho.
94. Conceitos integrados
Uma galáxia vizinha gira em seu eixo para que as estrelas de um lado se movam em nossa direção até 200 km/s, enquanto as do outro lado se afastam até 200 km/s. Isso faz com que a radiação EM que recebemos seja deslocada pelo Doppler por velocidades em toda a faixa de ± 200 km/s. Que faixa de comprimentos de onda teremos observe a linha de 656,0 nm na série Balmer de hidrogênio emitido por estrelas nesta galáxia. (Isso é chamado de ampliação de linha.)
95. Conceitos integrados
Um pulsar é um remanescente de uma supernova que gira rapidamente. Ele gira em seu eixo, varrendo o hidrogênio junto com ele para que o hidrogênio de um lado se mova em nossa direção tão rápido quanto 50,0 km/s, enquanto o do outro lado se afaste tão rápido quanto 50,0 km/s. Isso significa que a radiação EM que recebemos será deslocada por Doppler em uma faixa de\(\displaystyle ±50.0 km/s\). Que faixa de comprimentos de onda observaremos para a linha de 91,20 nm na série Lyman de hidrogênio? (Esse alargamento da linha é observado e, na verdade, fornece parte da evidência de rotação rápida.)
Solução de
91,18 nm a 91,22 nm
96. Conceitos integrados
Prove que a velocidade das partículas carregadas que se movem ao longo de um caminho reto através de campos elétricos e magnéticos perpendiculares é\(\displaystyle v=E/B\). Assim, campos elétricos e magnéticos cruzados podem ser usados como um seletor de velocidade independente da carga e da massa da partícula envolvida.
97. Resultados irracionais
(a) Qual voltagem deve ser aplicada a um tubo de raios-X para obter raios-X de comprimento de onda de 0,0100 fm para uso na exploração dos detalhes dos núcleos?
(b) O que não é razoável nesse resultado?
(c) Quais suposições são irracionais ou inconsistentes?
Solução
(a)\(\displaystyle 1.24×10^{11}V\)
(b) A tensão é extremamente grande em comparação com qualquer valor prático.
(c) A suposição de um comprimento de onda tão curto por esse método não é razoável.
98. Resultados irracionais
Um estudante em um laboratório de física observa um espectro de hidrogênio com uma grade de difração com o objetivo de medir os comprimentos de onda da radiação emitida. No espectro, ela observa uma linha amarela e descobre que seu comprimento de onda é 589 nm.
(a) Supondo que isso faça parte da série Balmer\(\displaystyle n_i\), determine o número quântico principal do estado inicial.
(b) O que não é razoável nesse resultado?
(c) Quais suposições são irracionais ou inconsistentes?
99. Construa seu próprio problema
A coroa solar é tão quente que a maioria dos átomos nela são ionizados. Considere um átomo semelhante ao hidrogênio na coroa que tem apenas um único elétron. Construa um problema no qual você calcule energias espectrais e comprimentos de onda selecionados de Lyman, Balmer ou outra série desse átomo que possa ser usada para identificar sua presença em um gás muito quente. Você precisará escolher o número atômico do átomo, identificar o elemento e escolher quais linhas espectrais considerar.
100. Construa seu próprio problema
Considere o espectro de hidrogênio deslocado pelo Doppler recebido de uma galáxia em rápido recuo. Construa um problema no qual você calcule as energias das linhas espectrais selecionadas na série Balmer e examine se elas podem ser descritas com uma fórmula como a da equação\(\displaystyle \frac{1}{λ}=R(\frac{1}{n^2_f}−\frac{1}{n^2_i})\), mas com uma constante diferente\(\displaystyle R\).


