30.8: Números e regras quânticas
- Page ID
- 194150
Objetivos de
Ao final desta seção, você poderá:
- Defina o número quântico.
- Calcule o ângulo do vetor de momento angular com um eixo.
- Defina o número quântico de spin.
As características físicas que são quantizadas — como energia, carga e momento angular — são de tal importância que lhes são dados nomes e símbolos. Os valores das entidades quantizadas são expressos em termos de números quânticos, e as regras que os governam são de extrema importância para determinar o que a natureza é e faz. Esta seção aborda alguns dos números e regras quânticos mais importantes — todos aplicados em química, ciência de materiais e muito além do reino da física atômica, onde foram descobertos pela primeira vez. Mais uma vez, vemos como a física faz descobertas que permitem que outros campos cresçam.
Os estados de energia dos sistemas vinculados são quantizados, porque o comprimento de onda da partícula pode caber nos limites do sistema de apenas algumas maneiras. Isso foi elaborado para o átomo de hidrogênio, para o qual as energias permitidas são expressas como
\[E_{n} \propto \frac{1}{n^{2}},\label{30.9.1}\]
onde\(n = 1,2,3, \cdot \cdot \cdot\). Definimos\(n\) como o número quântico principal que rotula os estados básicos de um sistema. O estado de menor energia tem\(n = 1\), o primeiro estado excitado tem\(n=2\), e assim por diante. Assim, os valores permitidos para o número quântico principal são
\[n = 1, 2, 3, ...\label{30.9.2}\]
Isso é mais do que apenas um esquema de numeração, pois a energia do sistema, como o átomo de hidrogênio, pode ser expressa como alguma função de\(n\), assim como outras características (como os raios orbitais do átomo de hidrogênio).
O fato de a magnitude do momento angular ser quantizada foi reconhecido pela primeira vez por Bohr em relação ao átomo de hidrogênio; agora se sabe que é verdade em geral. Com o desenvolvimento da mecânica quântica, verificou-se que a magnitude do momento angular só\(L\) pode ter os valores
\[L = \sqrt{l \left( l+1 \right) } \frac{h}{2\pi} \left(l = 0, 1, 2, ..., n-1\right), \label{30.9.3}\]
onde\(l\) é definido como o número quântico do momento angular. A regra para\(l\) em átomos é dada entre parênteses. Dado\(n\), o valor\(l\) pode ser qualquer número inteiro de zero até\(n-1\). Por exemplo, se\(n = 4\), então\(l\) pode ser 0, 1, 2 ou 3.
Observe que para\(n = 1\), só\(l\) pode ser zero. Isso significa que o momento angular fundamental para o hidrogênio é na verdade zero, não\(h/2\pi\) como Bohr propôs. A imagem das órbitas circulares não é válida, porque haveria momento angular para qualquer órbita circular. Uma imagem mais válida é a nuvem de probabilidade mostrada para o estado fundamental do hidrogênio neste link. Na verdade, o elétron passa o tempo dentro e perto do núcleo. A razão pela qual o elétron não permanece no núcleo está relacionada ao princípio da incerteza de Heisenberg — a energia do elétron teria que ser muito grande para ficar confinada ao pequeno espaço do núcleo. Agora, o primeiro estado excitado do hidrogênio tem\(n=2\), então isso\(l\) pode ser 0 ou 1, de acordo com a regra na Equação\(\ref{30.9.3}\). Da mesma forma\(n =3\), for,\(l\) pode ser 0, 1 ou 2. Geralmente, é mais conveniente declarar o valor de\(l\), um número inteiro simples, em vez de calcular o valor\(L\) da Equação\(\ref{30.9.3}\). Por exemplo, para\(l = 2\), vemos que
\[L = \sqrt{l \left( l+1 \right) } \frac{h}{2\pi} = \sqrt{6} \frac{h}{2 \pi} = 0.390 h = 2.58 \times 10^{-34} J \cdot s.\]
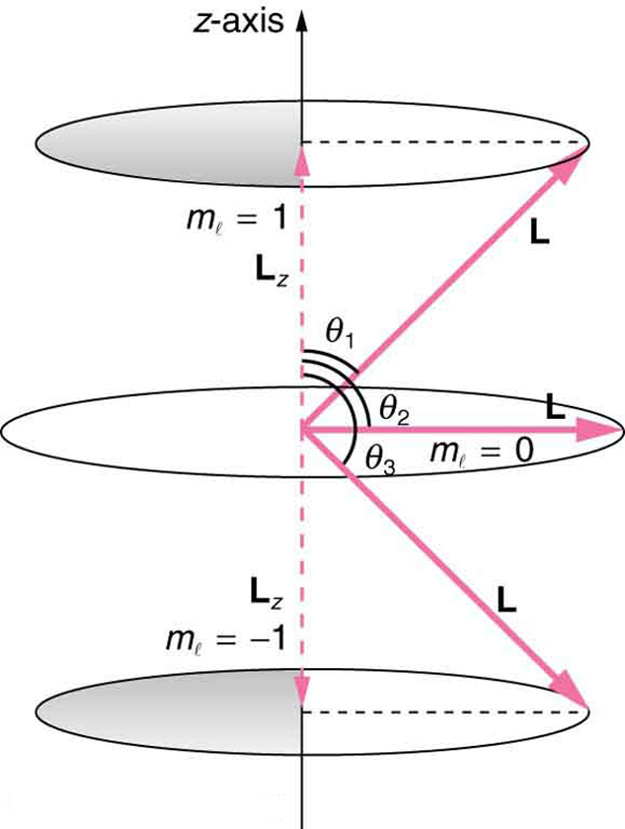
É muito mais simples de declarar\(l = 2\). Conforme reconhecido no efeito Zeeman, a direção do momento angular é quantizada. Agora sabemos que isso é verdade em todas as circunstâncias. Verifica-se que o componente do momento angular ao longo de uma direção no espaço, geralmente chamado de eixo -, pode ter apenas certos valores de\(L_{z}\). A direção no espaço deve estar relacionada a algo físico, como a direção do campo magnético naquele local. Esse é um aspecto da relatividade. A direção não tem significado se não há nada que varie com a direção, assim como a força magnética. Os valores permitidos de\(L_{z}\) são\[L_{z} = m_{l} \frac{h}{2\pi} \left( m_{l} = -l, -l + 1, ..., -1, 0, 1, ... l-1, l\right),\label{30.9.4}\] onde\(L_{z}\) está o componente z do momento angular e\(m_{l}\) é o número quântico da projeção do momento angular. A regra entre parênteses para os valores de\(m_{l}\) é que eles podem variar de\(-l\) até\(l\) em etapas de um. Por exemplo, if\(l = 2\), então\(m_{l}\) pode ter os cinco valores —2, —1, 0, 1 e 2. Cada um\(m_{l}\) corresponde a uma energia diferente na presença de um campo magnético, de modo que eles estão relacionados à divisão das linhas espectrais em partes discretas, conforme discutido na seção anterior. Se o componente\(z\) - do momento angular puder ter apenas certos valores, o momento angular poderá ter apenas certas direções, conforme ilustrado na Figura 30.9.1.
Exemplo\(\PageIndex{1}\): What are the Allowed Directions?
Calcule os ângulos que o vetor de momento angular\(L\) pode criar com o eixo z para\(l = 1\), conforme ilustrado na Figura 30.9.1.
Estratégia:
A Figura 30.9.1. representa os vetores\(L\) e,\(L_{z}\) como de costume, com setas proporcionais às suas magnitudes e apontando nas direções corretas. \(L\)e\(L_{z}\) formam um triângulo reto,\(L\) sendo a hipotenusa e\(L_{z}\) o lado adjacente. Isso significa que a razão de\(L_{z}\) para\(L\) é o cosseno do ângulo de interesse. Podemos encontrar\(L\) e\(L_{z}\) usar\(L = \sqrt{l\left(l + 1\right)}\frac{h}{2\pi}\)\(L_{z} = m \frac{h}{2\pi}\) e.
Solução
Nós somos dados\(l = 1\), então isso\(m_{l}\) pode ser =1, 0 ou -1. Assim,\(L\) tem o valor dado por\(L = \sqrt{l\left(l + 1\right)}\frac{h}{2\pi}\).
\[L = \frac{\sqrt{l\left(l + 1\right)}h}{2\pi} = \frac{\sqrt{2}h}{2\pi} \label{30.9.5}\]
\(L_{z}\)pode ter três valores, dados por\(L_{z} = m_{l} \frac{h}{2\pi}\). \[L_{z} = m_{l} \frac{h}{2\pi} = \begin{cases} \frac{h}{2\pi}, ~ m_{l} = +1 \\[2ex] 0, ~ m_{l} = 0 \\[2ex] \frac{h}{2\pi}, ~ m_{l} = -1 \end{cases} \label{30.9.6}\]
Como pode ser visto na Figura\(\cos{\theta} = L_{z}/L\), e assim por diante\(m_{l} \pm 1\), temos\[\cos{\theta_{1}} = \frac{L_{z}}{L} = \frac{\frac{h}{2\pi}}{\frac{\sqrt{2}h}{2\pi}} = \frac{1}{\sqrt{2}} = -.707.\label{30.9.7}\]
Assim,
\[\theta_{1} = \cos{0.707}^{-1} = 45.0 ^{\circ}.\label{30.9.8}\]
Da mesma forma\(m_{l} = 0\), para, encontramos\(\cos_{2} = 0\); assim,
\[\theta_{2} = \cos{0}^{-1} = 90.0. ^{\circ} \label{30.9.9}\]
E para\(m_{l} = -1\),
\[\cos{\theta_{3}} = \frac{L_{z}}{L} = \frac{-\frac{h}{2\pi}}{\frac{\sqrt{2}h}{2\pi}} = -\frac{1}{\sqrt{2}} = -0.707, \label{30.9.10}\]
para que
\[\theta_{3} = \cos{\left(-0.707\right)}^{-1} = 135.0^{\circ}.\label{30.9.11}\]
Discussão:
Os ângulos são consistentes com a figura. Somente o ângulo em relação ao eixo z é quantizado. \(L\)pode apontar em qualquer direção, desde que faça o ângulo adequado com o eixo z. Assim, os vetores de momento angular estão nos cones, conforme ilustrado. Esse comportamento não é observado em grande escala. Para ver como o princípio da correspondência se mantém aqui, considere que o menor ângulo (\(\theta_{1}\)no exemplo) é para o valor máximo de\(m_{l} = 0\), ou seja,\(m_{l} = l\). Para esse menor ângulo,
\[\cos{\theta} = \frac{L_{z}}{L} = \frac{l}{\sqrt{l\left(l + 1 \right) }},\label{30.9.12}\]
que se aproxima de 1 quando\(l\) se torna muito grande. Se\(\cos{\theta} = 1\), então\(\theta = 0^{\circ}\). Além disso, para grandes\(l\), existem muitos valores de\(m_{l}\), de modo que todos os ângulos se tornam possíveis à medida que\(l\) se tornam muito grandes.
O momento angular do spin intrínseco é quantizado em magnitude e direção
Há mais dois números quânticos que causam preocupação imediata. Ambos foram descobertos pela primeira vez para elétrons em conjunto com uma estrutura fina em espectros atômicos. Agora está bem estabelecido que elétrons e outras partículas fundamentais têm spin intrínseco, aproximadamente análogo a um planeta girando em seu eixo. Esse spin é uma característica fundamental das partículas, e somente uma magnitude de rotação intrínseca é permitida para um determinado tipo de partícula. O momento angular intrínseco é quantizado independentemente do momento angular orbital. Além disso, a direção do giro também é quantizada. Foi descoberto que a magnitude do momento angular de rotação intrínseco (interno),\(S\), de um elétron é dada por
\[S = \sqrt{s\left(s+1\right)}\frac{h}{2\pi} \left( s = 1/2 ~ for ~ electrons\right), \label{30.9.13}\]
onde\(s\) é definido como o número quântico de spin. Isso é muito semelhante à quantização de\(L\) dado em\(L = \sqrt{l\left(l+1\right)}\frac{h}{2\pi}\), exceto que o único valor permitido\(s\) para elétrons é 1/2.
A direção do spin intrínseco é quantizada, assim como a direção do momento angular orbital. A direção do momento angular de rotação ao longo de uma direção no espaço, novamente chamada de eixo z, pode ter apenas os valores
\[s_{z} = m_{s} \frac{h}{2\pi} \left( m_{s} = -\frac{1}{2}, +\frac{1}{2} \right) \label{30.9.14}\]
para elétrons. \(s_{z}\0 is the z-component of spin angular momentum and \(m_{s}\)é o número quântico da projeção de spin. Para elétrons, só\(s\) pode ser 1/2 e\(m_{s}\) pode ser +1/2 ou —1/2. A projeção de rotação\(m_{s} = + 1/2\) é chamada de rotação para cima, enquanto que\(m_{s} = -1/2\)\(m_{s} = - 1/2\) é chamada de rotação para baixo. Eles estão ilustrados neste link.
ROTAÇÃO INTRÍNSECA
Nos capítulos posteriores, veremos que o spin intrínseco é uma característica de todas as partículas subatômicas. Para algumas partículas\(s\) é meio integral, enquanto para outras\(s\) é integral — existem diferenças cruciais entre partículas de spin semi-integrais e partículas de spin integrais. Prótons e nêutrons, como elétrons, têm\(s = 1/2\), enquanto fótons têm\(s = 1\), e outras partículas chamadas píons têm\(s = 0\), e assim por diante.
Para resumir, o estado de um sistema, como a natureza precisa de um elétron em um átomo, é determinado por seus números quânticos específicos. Eles são expressos na forma\(n, l, m_{l}, m_{s}\) - veja a tabela Para elétrons em átomos, o número quântico principal pode ter os valores\(n = 1, 2, 3, ...\). Uma vez\(n\) conhecidos, os valores do número quântico do momento angular são limitados\(l = 1, 2, 3, ..., n-1\) a. Para um determinado valor de\(l\), o número quântico da projeção de momento angular pode ter apenas os valores\(m_{l} = -l, -l + 1, ..., -1, 0, 1, ..., l-1, l\). O spin do elétron é independente de\(n\)\(l\), e\(m_{l}\), sempre tendo\(s = 1/2\). O número quântico da projeção de spin pode ter dois valores. \(m_{s} = 1/2 ~ or ~ -1/2\).
| Nome | Símbolo | Valores permitidos |
|---|---|---|
| Número quântico principal | \(n\) | \(1,2,3,...\) |
| Momento angular | \(l\) | \(0, 1, 2, ... n-1\) |
| Projeção de momento angular | \(m_{l}\) | \(-l, -l+1, ..., -1, 0, 1, ..., l-1, l \left(or ~ 0, \pm 1, \pm 2, ..., \pm l \right)\) |
| Girar | \(s\) | \(1/2 \left(electrons\right)\) |
| Projeção de rotação | \(m_{s}\) | \(\pm 1/2\) |
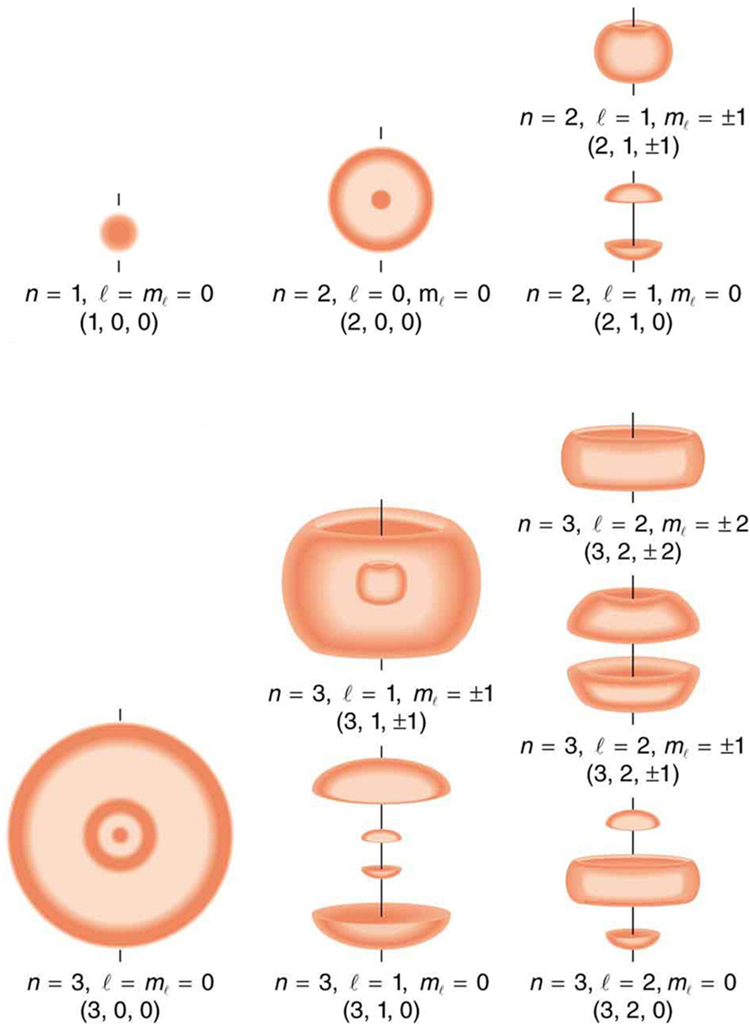
A Figura 30.9.2. mostra vários estados de hidrogênio correspondentes a diferentes conjuntos de números quânticos. Observe que essas nuvens de probabilidade são as localizações dos elétrons, conforme determinado ao fazer medições repetidas - cada medição encontra o elétron em um local definido, com uma chance maior de encontrar o elétron em alguns lugares do que em outros. Com medições repetidas, surge o padrão de probabilidade mostrado na figura. As nuvens de probabilidade não parecem nem correspondem às órbitas clássicas. O princípio da incerteza na verdade impede que nós e a natureza saibamos como o elétron vai de um lugar para outro e, portanto, uma órbita realmente não existe como tal. A natureza em pequena escala é novamente muito diferente daquela em grande escala.
Veremos que os números quânticos discutidos nesta seção são válidos para uma ampla gama de partículas e outros sistemas, como núcleos. Alguns números quânticos, como o spin intrínseco, estão relacionados às classificações fundamentais das partículas subatômicas e obedecem a leis que nos darão mais informações sobre a subestrutura da matéria e suas interações.
EXPLORAÇÕES DE PHET: EXPERIMENTO STERN-GERLACH
O experimento clássico de Stern-Gerlach mostra que os átomos têm uma propriedade chamada spin. O spin é um tipo de momento angular intrínseco, que não tem contrapartida clássica. Quando o componente z do spin é medido, sempre se obtém um dos dois valores: giro para cima ou para baixo.

Resumo
- Os números quânticos são usados para expressar os valores permitidos de entidades quantizadas. O número quântico principal\(n\) rotula os estados básicos de um sistema e é dado por\(n = 1, 2, 3, ... \)
- A magnitude do momento angular é dada por\(L = \sqrt{l \left( l+1 \right) } \frac{h}{2\pi} \left(l = 0, 1, 2, ..., n-1\right),\) onde\(l\) está o número quântico do momento angular. A direção do momento angular é quantizada, na medida em que seu componente ao longo de um eixo definido por um campo magnético, chamado eixo z,\(L_{z}\) é dado por\(L_{z} = m_{l} \frac{h}{2\pi} ~ \left(m_{l} = -l, -l+1, ..., -1, 0, 1, ... l-1, l\right),\) onde está o componente z do momento angular e\(m_{l}\) é o número quântico da projeção do momento angular. Da mesma forma, o momento angular de spin intrínseco do elétron\(S\) é dado por\(S = \sqrt{s\left(s+1\right)}\frac{h}{2\pi} ~ \left(s = 1/2 ~ for ~ electrons \right),\) onde\(S_{z}\) está o componente z do momento angular de spin e\(m_{s}\) é o número quântico da projeção de spin. A projeção de rotação\(m_{s} = +1/2\) é chamada de rotação para cima, enquanto\(m_{s} = -1/2\) é chamada de rotação para baixo. A tabela resume os números quânticos atômicos e seus valores permitidos.


