Skip to main content
Global

30.7: Padrões em espectros revelam mais quantização

  1. Last updated
  2. Save as PDF
  • Page ID
    194152

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Declare e discuta o efeito Zeeman.
    • Defina o campo magnético orbital.
    • Defina o momento angular orbital.
    • Defina a quantização do espaço.

    Medições de alta resolução dos espectros atômicos e moleculares mostram que as linhas espectrais são ainda mais complexas do que parecem à primeira vista. Nesta seção, veremos que essa complexidade gerou novas informações importantes sobre elétrons e suas órbitas nos átomos.

    Para explorar a subestrutura dos átomos (e sabendo que os campos magnéticos afetam as cargas móveis), o físico holandês Hendrik Lorentz (1853-1930) sugeriu que seu aluno Pieter Zeeman (1865-1943) estudasse como os espectros podem ser afetados por campos magnéticos. O que eles descobriram ficou conhecido como efeito Zeeman, que envolveu linhas espectrais sendo divididas em duas ou mais linhas de emissão separadas por um campo magnético externo, conforme mostrado na Figura\(\PageIndex{1}\). Por suas descobertas, Zeeman e Lorentz dividiram o Prêmio Nobel de Física de 1902.

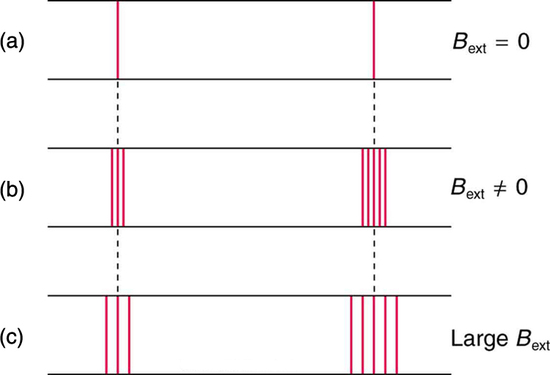
    A figura mostra o efeito do campo magnético nas linhas espectrais. No primeiro caso, duas linhas espectrais são mostradas quando não há campo magnético externo. No segundo caso, quando o campo magnético é aplicado, as linhas espectrais se dividem em várias linhas; a linha à esquerda se divide em três linhas. A linha à direita se divide em cinco. No terceiro caso, o campo magnético é grande. A linha esquerda é novamente dividida em três linhas e a direita em cinco, mas as linhas divididas estão mais afastadas do que quando o campo magnético externo não é tão forte.
    Figura\(\PageIndex{1}\): O efeito Zeeman é a divisão das linhas espectrais quando um campo magnético é aplicado. O número de linhas formadas varia, mas a dispersão é proporcional à força do campo aplicado. (a) Duas linhas espectrais sem campo magnético externo. (b) As linhas se dividem quando o campo é aplicado. (c) A divisão é maior quando um campo mais forte é aplicado.

    A divisão de Zeeman é complexa. Algumas linhas se dividem em três linhas, algumas em cinco e assim por diante. Mas uma característica geral é que a quantidade de separação das linhas divididas é proporcional à intensidade do campo aplicado, indicando uma interação com uma carga em movimento. A divisão significa que a energia quantizada de uma órbita é afetada por um campo magnético externo, fazendo com que a órbita tenha várias energias discretas em vez de uma. Mesmo sem um campo magnético externo, medições muito precisas mostraram que as linhas espectrais são duplas (divididas em duas), aparentemente por campos magnéticos dentro do próprio átomo.

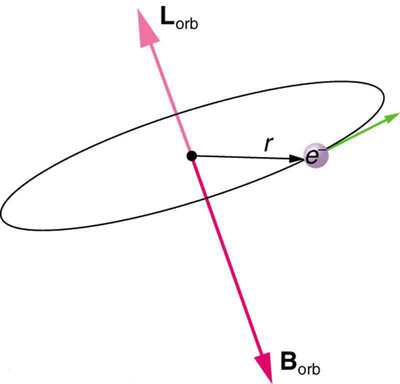
    A figura mostra um elétron viajando em uma órbita circular com raio r. Um suborbe do campo magnético B é orientado para baixo e o suborbe do momento angular orbital L é orientado ao longo da mesma linha, mas para cima, em uma direção oposta à sub-esfera B.
    Figura\(\PageIndex{2}\): A imagem aproximada de um elétron em uma órbita circular ilustra como o circuito de corrente produz seu próprio campo magnético, chamado\(B_{orb}\). Também mostra como\(B_{orb}\) está na mesma linha do momento angular orbital\(L_{orb}\).

    A teoria de órbitas circulares de Bohr é útil para visualizar como a órbita de um elétron é afetada por um campo magnético. A órbita circular forma um circuito de corrente, que cria um campo magnético próprio,\(B_{orb}\) como visto na Figura\(\PageIndex{2}\). Observe que o campo magnético orbital\(B_{orb}\) e o momento angular orbital\(L_{orb}\) estão na mesma linha. O campo magnético externo e o campo magnético orbital interagem; um torque é exercido para alinhá-los. Um torque girando um sistema em algum ângulo funciona para que haja energia associada a essa interação. Assim, órbitas em ângulos diferentes em relação ao campo magnético externo têm energias diferentes. O que é notável é que as energias são quantizadas — o campo magnético divide as linhas espectrais em várias linhas discretas que têm energias diferentes. Isso significa que apenas certos ângulos são permitidos entre o momento angular orbital e o campo externo, conforme visto na Figura\(\PageIndex{3}\).

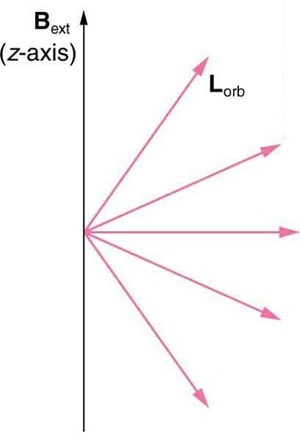
    Um campo magnético externo ao longo do eixo z vertical é mostrado. Várias linhas espectrais são mostradas originadas do mesmo ponto no eixo z que representa o momento angular orbital.
    Figura\(\PageIndex{3}\): Somente certos ângulos são permitidos entre o momento angular orbital e um campo magnético externo. Isso está implícito no fato de que o efeito Zeeman divide as linhas espectrais em várias linhas discretas. Cada linha está associada a um ângulo entre o campo magnético externo e os campos magnéticos devido aos elétrons e suas órbitas.

    Já sabemos que a magnitude do momento angular é quantizada para órbitas de elétrons em átomos. A nova visão é que a direção do momento angular orbital também é quantizada. O fato de o momento angular orbital poder ter apenas certas direções é chamado de quantização espacial. Como muitos aspectos da mecânica quântica, essa quantização da direção é totalmente inesperada. Na escala macroscópica, o momento angular orbital, como o da lua ao redor da Terra, pode ter qualquer magnitude e estar em qualquer direção.

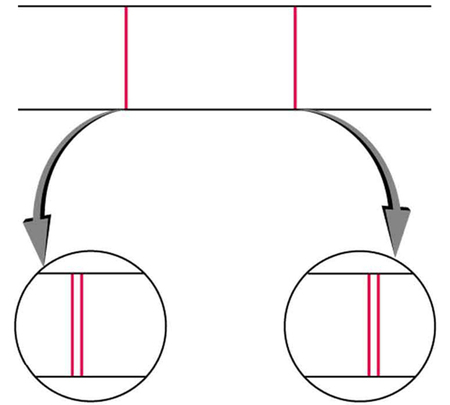
    A imagem a mostra uma visão ampliada de duas linhas espectrais. A visão ampliada mostra que essas linhas espectrais são duplas, o que significa que duas linhas paralelas estão sendo colocadas juntas. Na imagem b, é mostrada uma estrutura na qual as ondas concêntricas estão se expandindo.
    Figura\(\PageIndex{4}\): Estrutura fina. Após um exame minucioso, as linhas espectrais são duplas, mesmo na ausência de um campo magnético externo. O elétron tem um campo magnético intrínseco que interage com seu campo magnético orbital.

    O tratamento detalhado da quantização espacial começou a explicar algumas complexidades dos espectros atômicos, mas certos padrões pareciam ser causados por outra coisa. Conforme mencionado, as linhas espectrais são, na verdade, dupletos bem espaçados, uma característica chamada estrutura fina, conforme mostrado na Figura\(\PageIndex{4}\). O gibão muda quando um campo magnético é aplicado, o que implica que qualquer causa o gibão interage com um campo magnético. Em 1925, Sem Goudsmit e George Uhlenbeck, dois físicos holandeses, argumentaram com sucesso que os elétrons têm propriedades análogas a uma carga macroscópica girando em seu eixo. Os elétrons, na verdade, têm um momento angular interno ou intrínseco chamado spin intrínseco\(S\). Como os elétrons são carregados, seu spin intrínseco cria um campo magnético intrínseco\(B_{orb}\), que interage com seu campo magnético orbital\(B_{orb}\). Além disso, o spin intrínseco do elétron é quantizado em magnitude e direção, análoga à situação do momento angular orbital. O spin do elétron pode ter apenas uma magnitude e sua direção pode estar em apenas um dos dois ângulos em relação a um campo magnético, conforme visto na Figura\(\PageIndex{5}\). Nós nos referimos a isso como spin up ou spin down do elétron. Cada direção de rotação tem uma energia diferente; portanto, as linhas espectroscópicas são divididas em duas. Os dupletos espectrais agora são entendidos como sendo devidos ao spin do elétron.

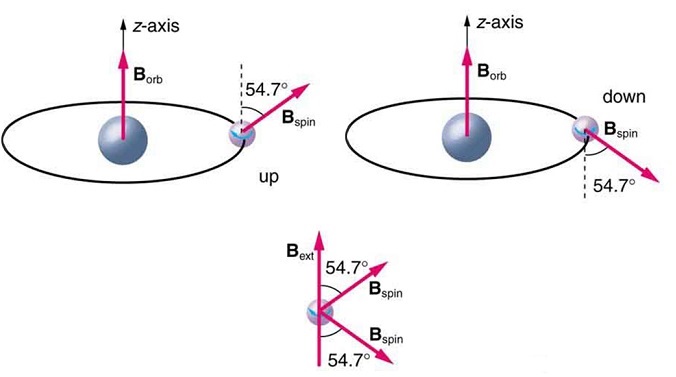
    A imagem mostra dois casos de campo magnético intrínseco de um elétron devido ao seu spin. No primeiro caso, a órbita circular é mostrada com campo magnético externo na direção vertical e a direção do campo magnético intrínseco do elétron devido ao seu giro é para cima em um ângulo de cinquenta e quatro pontos e sete graus com o eixo vertical. No segundo caso, a órbita circular é mostrada com campo magnético externo na direção vertical e a direção do campo magnético intrínseco do elétron devido ao seu giro é para baixo em um ângulo de cinquenta e quatro pontos e sete graus com o eixo vertical.
    Figura\(\PageIndex{5}\): O campo magnético intrínseco\(B_{orb}\) de um elétron é atribuído ao seu spin\(S\), aproximadamente representado como sendo devido à sua carga girando em seu eixo. Este é apenas um modelo bruto, já que os elétrons parecem não ter tamanho. O spin e o campo magnético intrínseco do elétron podem formar apenas um dos dois ângulos com outro campo magnético, como o criado pelo movimento orbital do elétron. O espaço é quantizado tanto para rotação quanto para momento angular orbital.

    Esses dois novos insights - que a direção do momento angular, seja orbital ou spin, é quantizada e que os elétrons têm spin intrínseco - ajudam a explicar muitas das complexidades dos espectros atômicos e moleculares. Na ressonância magnética, é a forma como o campo magnético intrínseco do hidrogênio e dos átomos biológicos interagem com um campo externo que está subjacente aos fundamentos do diagnóstico.

    Resumo

    • O efeito Zeeman — a divisão das linhas quando um campo magnético é aplicado — é causado por outras entidades quantizadas nos átomos.
    • Tanto a magnitude quanto a direção do momento angular orbital são quantizadas.
    • O mesmo vale para a magnitude e direção do spin intrínseco dos elétrons.

    Glossário

    Efeito Zeeman
    o efeito dos campos magnéticos externos nas linhas espectrais
    rotação intrínseca
    o momento angular interno ou intrínseco dos elétrons
    momento angular orbital
    um momento angular que corresponde ao análogo quântico do momento angular clássico
    estrutura fina
    a divisão das linhas espectrais do espectro de hidrogênio quando as linhas espectrais são examinadas em resolução muito alta
    quantização espacial
    o fato de que o momento angular orbital pode ter apenas certas direções
    campo magnético intrínseco
    o campo magnético gerado devido ao spin intrínseco dos elétrons
    campo magnético orbital
    o campo magnético gerado devido ao movimento orbital dos elétrons