30.6: A natureza ondulatória da matéria causa quantização

Objetivos de

Ao final desta seção, você poderá:

• Explique o modelo de átomo de Bohr.
• Defina e descreva a quantização do momento angular.
• Calcule o momento angular para uma órbita de átomo.
• Defina e descreva as propriedades ondulatórias da matéria.

Depois de visitar algumas das aplicações de diferentes aspectos da física atômica, agora retornamos à teoria básica que foi construída sobre o átomo de Bohr. Einstein disse certa vez que era importante continuar fazendo as perguntas que acabamos ensinando as crianças a não fazerem. Por que o momento angular é quantizado? Você já sabe a resposta. Os elétrons têm propriedades ondulatórias, como propôs mais tarde de Broglie. Eles só podem existir onde interferem de forma construtiva e somente certas órbitas atendem às condições adequadas, como veremos no próximo módulo.

Após o trabalho inicial de Bohr sobre o átomo de hidrogênio, uma década se passaria antes de Broglie propor que a matéria tem propriedades de onda. As propriedades ondulatórias da matéria foram posteriormente confirmadas por observações de interferência eletrônica quando espalhada pelos cristais. Os elétrons só podem existir em locais onde interferem de forma construtiva. Como isso afeta os elétrons nas órbitas atômicas? Quando um elétron está ligado a um átomo, seu comprimento de onda deve caber em um espaço pequeno, algo como uma onda estacionária em uma corda. (Veja a Figura.) Órbitas permitidas são aquelas em que um elétron interfere construtivamente consigo mesmo. Nem todas as órbitas produzem interferência construtiva. Assim, somente certas órbitas são permitidas — as órbitas são quantizadas.

Figura\(\PageIndex{1}\): (a) As ondas em uma corda têm um comprimento de onda relacionado ao comprimento da corda, permitindo que elas interfiram de forma construtiva. (b) Se imaginarmos a corda dobrada em um círculo fechado, teremos uma ideia aproximada de como os elétrons em órbitas circulares podem interferir de forma construtiva. (c) Se o comprimento de onda não se encaixar na circunferência, o elétron interfere destrutivamente; ele não pode existir em tal órbita.

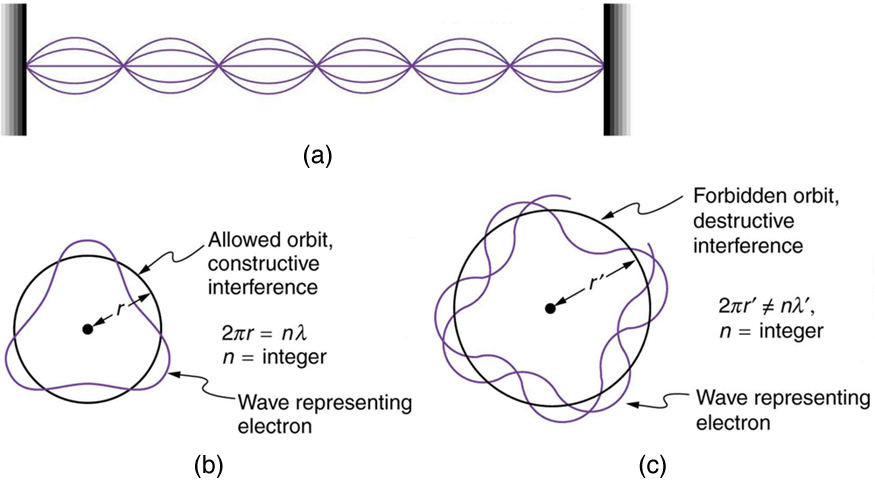
Para uma órbita circular, a interferência construtiva ocorre quando o comprimento de onda do elétron se encaixa perfeitamente na circunferência, de modo que as cristas das ondas sempre se alinham com as cristas e as calhas das ondas se alinham com as calhas, conforme mostrado na Figura (b). Mais precisamente, quando um múltiplo integral do comprimento de onda do elétron é igual à circunferência da órbita, a interferência construtiva é obtida. Na forma de equação, a condição para interferência construtiva e uma órbita eletrônica permitida é

\[n \lambda_n = 2 \pi r_n (n = 1, \, 2, \, 3, ...),\]onde\(\lambda_n\) é o comprimento de onda do elétron e\(r_n\) é o raio dessa órbita circular. O comprimento de onda de Broglie é\(\lambda = h/p = h/mv\), e então aqui\(\lambda = h/m_e v\). Substituir isso na condição anterior por interferência construtiva produz um resultado interessante:

\[\dfrac{nh}{m_ev} = 2\pi r_n.\]Reorganizando os termos e observando que,\(L = mvr\) para uma órbita circular, obtemos a quantização do momento angular como condição para órbitas permitidas:

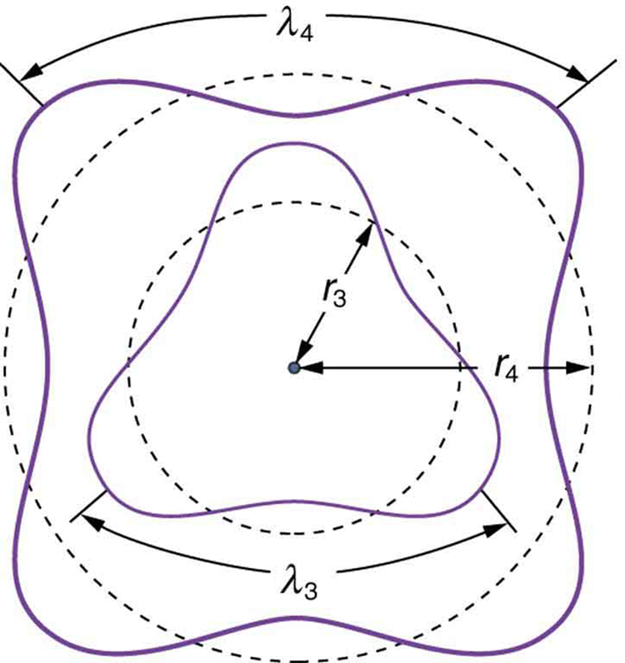
\[L = m_e vr_n = n\dfrac{h}{2\pi} (n = 1, \, 2, \, 3, ...).\]Isso é o que Bohr foi forçado a hipotetizar como regra para órbitas permitidas, conforme declarado anteriormente. Agora percebemos que é a condição para a interferência construtiva de um elétron em uma órbita circular. A figura ilustra isso para\(n = 3\)\(n = 4\) e.

Ondas e quantização

A natureza ondulatória da matéria é responsável pela quantização dos níveis de energia em sistemas vinculados. Somente os estados em que a matéria interfere de forma construtiva existem ou são “permitidos”. Como há uma órbita mais baixa onde isso é possível em um átomo, o elétron não pode entrar em espiral no núcleo. Ele não pode existir perto ou dentro do núcleo. A natureza ondulatória da matéria é o que impede o colapso da matéria e dá aos átomos seus tamanhos.

Figura: A\(\PageIndex{2}\) terceira e a quarta órbitas circulares permitidas têm três e quatro comprimentos de onda, respectivamente, em suas circunferências.

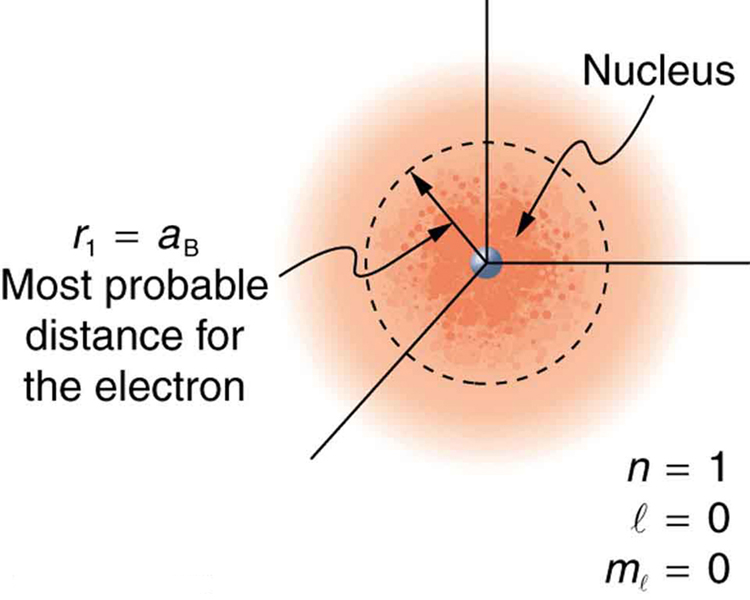
Por causa do caráter ondulatório da matéria, a ideia de órbitas bem definidas dá lugar a um modelo no qual há uma nuvem de probabilidade, consistente com o princípio da incerteza de Heisenberg. A figura mostra como isso se aplica ao estado fundamental do hidrogênio. Se você tentar seguir o elétron em uma órbita bem definida usando uma sonda que tenha um comprimento de onda pequeno o suficiente para obter alguns detalhes, você expulsará o elétron de sua órbita. Cada medição da posição do elétron descobrirá que ele está em um local definido em algum lugar próximo ao núcleo. Medições repetidas revelam uma nuvem de probabilidade como a da figura, com cada partícula sendo a localização determinada por uma única medição. Não existe um tipo de distribuição de órbita circular bem definido. A natureza novamente se mostra diferente em pequena escala do que em escala macroscópica.

Figura\(\PageIndex{3}\): O estado fundamental de um átomo de hidrogênio tem uma nuvem de probabilidade descrevendo a posição de seu elétron. A probabilidade de encontrar o elétron é proporcional à escuridão da nuvem. O elétron pode estar mais próximo ou mais distante do que o raio de Bohr, mas é muito improvável que esteja a uma grande distância do núcleo.

Há muitos exemplos em que a natureza ondulatória da matéria causa quantização em sistemas ligados, como o átomo. Sempre que uma partícula está confinada ou limitada a um espaço pequeno, seus comprimentos de onda permitidos são aqueles que se encaixam nesse espaço. Por exemplo, a partícula em um modelo de caixa descreve uma partícula livre para se mover em um pequeno espaço cercado por barreiras impenetráveis. Isso é verdade em radiadores de corpo negro (átomos e moléculas), bem como em espectros atômicos e moleculares. Vários átomos e moléculas terão diferentes conjuntos de órbitas de elétrons, dependendo do tamanho e da complexidade do sistema. Quando um sistema é grande, como um grão de areia, as pequenas ondas de partículas nele podem se encaixar de tantas maneiras que se torna impossível ver que os estados permitidos são discretos. Assim, o princípio da correspondência é satisfeito. À medida que os sistemas se tornam grandes, eles gradualmente parecem menos granulados e a quantização se torna menos evidente. Sistemas não ligados (pequenos ou não), como um elétron liberado de um átomo, não têm energias quantizadas, pois seus comprimentos de onda não são limitados a caber em um determinado volume.

EXPLORAÇÕES PHET: INTERFERÊNCIA DE ONDAS QUÂNTICAS

Quando fótons, elétrons e átomos se comportam como partículas e quando se comportam como ondas? Observe as ondas se espalharem e interferirem ao passarem por uma fenda dupla e, em seguida, serem detectadas na tela como pequenos pontos. Use detectores quânticos para explorar como as medições alteram as ondas e os padrões que elas produzem na tela.

Figura\(\PageIndex{4}\): Interferência de onda quântica

Resumo

• A quantização da energia orbital é causada pela natureza ondulatória da matéria. As órbitas permitidas nos átomos ocorrem por interferência construtiva de elétrons na órbita, exigindo um número integral de comprimentos de onda para caber na circunferência de uma órbita; ou seja,\[n\lambda_n = 2\pi r_n (n = 1, \, 2, \, 3, ...),\] onde\(\lambda_n\) está o comprimento de onda de Broglie do elétron.
• Devido à natureza ondulatória dos elétrons e ao princípio da incerteza de Heisenberg, não há órbitas bem definidas; em vez disso, existem nuvens de probabilidade.
• Bohr propôs corretamente que a energia e os raios das órbitas dos elétrons nos átomos sejam quantizados, com energia para transições entre órbitas dada por\[\Delta E = hf = E_i - E_f,\] onde\(\Delta E\) está a mudança de energia entre as órbitas inicial e final e\(hf\) é a energia de um fóton absorvido ou emitido.
• É útil traçar as energias da órbita em um gráfico vertical chamado diagrama de nível de energia.
• As órbitas permitidas são circulares, propôs Bohr, e devem ter quantizado o momento angular orbital dado por\[L = m_evr_n = n\dfrac{h}{2\pi} (n = 1, \, 2, \, 3, . . .),\] onde\(L\) está o momento angular,\(r_n\) é o raio da órbita\(n\) e\(h\) é a constante de Planck.