29.7: Probabilidade e o Princípio da Incerteza de Heisenberg

Objetivos de

Ao final desta seção, você poderá:

• Use as duas versões do princípio da incerteza de Heisenberg nos cálculos.
• Explique as implicações do princípio de incerteza de Heisenberg para medições.

Matéria e fótons são ondas, o que significa que estão espalhados por alguma distância. Qual é a posição de uma partícula, como um elétron? Está no centro da onda? A resposta está em como você mede a posição de um elétron. Experimentos mostram que você encontrará o elétron em algum local definido, ao contrário de uma onda. Mas se você configurar exatamente a mesma situação e medi-la novamente, encontrará o elétron em um local diferente, geralmente muito longe de qualquer incerteza experimental em sua medição. Medições repetidas exibirão uma distribuição estatística de locais que aparecem em forma de onda (Figura\(\PageIndex{1}\)).

Figura\(\PageIndex{1}\): A construção do padrão de difração de elétrons espalhados pela superfície de um cristal. Cada elétron chega a uma localização definida, que não pode ser prevista com precisão. A distribuição geral mostrada na parte inferior pode ser prevista como a difração de ondas com o comprimento de onda de Broglie dos elétrons.

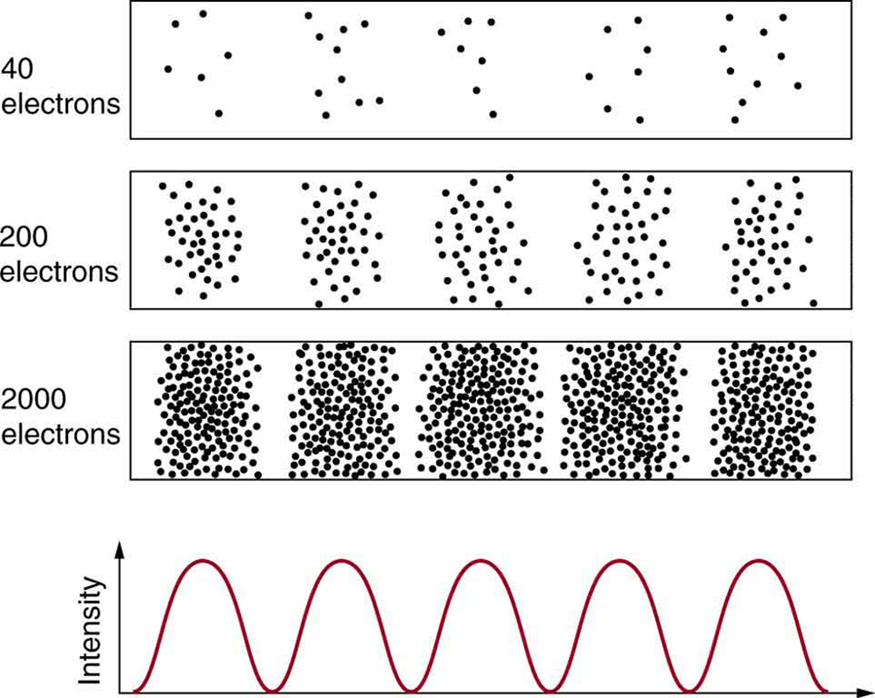
Depois que de Broglie propôs a natureza ondulatória da matéria, muitos físicos, incluindo Schrödinger e Heisenberg, exploraram as consequências. Surgiu rapidamente a ideia de que, devido ao seu caráter de onda, a trajetória e o destino de uma partícula não podem ser previstos com precisão para cada partícula individualmente. No entanto, cada partícula vai para um local definido (conforme ilustrado na Figura\(\PageIndex{2}\)). Depois de compilar dados suficientes, você obtém uma distribuição relacionada ao comprimento de onda e ao padrão de difração da partícula. Há uma certa probabilidade de encontrar a partícula em um determinado local, e o padrão geral é chamado de distribuição de probabilidade. Aqueles que desenvolveram a mecânica quântica criaram equações que previram a distribuição de probabilidade em várias circunstâncias.

Figura\(\PageIndex{2}\): A interferência de dupla fenda para elétrons (a) e fótons (b) é idêntica para comprimentos de onda iguais e separações de fenda iguais. Ambos os padrões são distribuições de probabilidade no sentido de que são construídos por partículas individuais atravessando o aparelho, cujos caminhos não são previsíveis individualmente.

É um tanto inquietante pensar que você não pode prever exatamente para onde uma partícula individual irá, nem mesmo segui-la até seu destino. Vamos explorar o que acontece se tentarmos seguir uma partícula. Considere os padrões de dupla fenda obtidos para elétrons e fótons na Figura\(\PageIndex{2}\). Primeiro, notamos que esses padrões são idênticos\(d \, sin \, \theta = m\lambda\), seguindo a equação da interferência construtiva de dupla fenda desenvolvida nas Energias de Fótons e no Espectro Eletromagnético, onde\(d\) está a separação da fenda e\(\lambda\) é o comprimento de onda do elétron ou fóton.

Ambos os padrões se acumulam estatisticamente à medida que partículas individuais caem no detector. Isso pode ser observado para fótons ou elétrons — por enquanto, vamos nos concentrar nos elétrons. Você pode imaginar que os elétrons estão interferindo uns com os outros, como qualquer onda. Para testar isso, você pode diminuir a intensidade até que nunca haja mais de um elétron entre as fendas e a tela. O mesmo padrão de interferência se acumula! Isso implica que a distribuição de probabilidade de uma partícula abrange as duas fendas e as partículas realmente interferem consigo mesmas. Isso também significa que o elétron passa pelas duas fendas? Um elétron é uma unidade básica da matéria que não é divisível. Mas é uma pergunta justa, então devemos verificar se o elétron atravessa uma fenda ou a outra, ou ambas. Uma possibilidade é ter bobinas ao redor das fendas que detectem cargas se movendo através delas. O que se observa é que um elétron sempre passa por uma fenda ou por outra; ele não se divide para passar por ambas. Mas há um problema. Se você determinar que o elétron passou por uma das fendas, não obterá mais um padrão de fenda dupla — em vez disso, obterá interferência de fenda única. Não há como escapar usando outro método para determinar por qual fenda o elétron passou. Saber que a partícula passou por uma fenda força um padrão de fenda única. Se você não observar por qual fenda o elétron passa, obterá um padrão de fenda dupla.

Incerteza de Heisenberg

Como saber por qual fenda o elétron passou muda o padrão? A resposta é fundamentalmente importante: a medição afeta o sistema que está sendo observado. As informações podem ser perdidas e, em alguns casos, é impossível medir duas quantidades físicas simultaneamente com precisão exata. Por exemplo, você pode medir a posição de um elétron em movimento espalhando luz ou outros elétrons a partir dele. Essas sondas têm impulso por si mesmas e, ao se espalharem pelo elétron, elas mudam seu momento de uma maneira que perde informações. Há um limite para o conhecimento absoluto, mesmo em princípio.

Figura\(\PageIndex{3}\): Werner Heisenberg foi um dos melhores físicos que desenvolveram a mecânica quântica inicial. Seu trabalho não só permitiu uma descrição da natureza em escala muito pequena, mas também mudou nossa visão da disponibilidade de conhecimento. Embora seja universalmente reconhecido por seu brilho e pela importância de seu trabalho (ele recebeu o Prêmio Nobel em 1932, por exemplo), Heisenberg permaneceu na Alemanha durante a Segunda Guerra Mundial e liderou o esforço alemão para construir uma bomba nuclear, alienando-se permanentemente da maioria da comunidade científica. (crédito: Autor desconhecido, via Wikimedia Commons)

Foi Werner Heisenberg quem primeiro declarou esse limite ao conhecimento em 1929 como resultado de seu trabalho sobre mecânica quântica e as características de onda de todas as partículas. (Figura\(\PageIndex{3}\)). Especificamente, considere medir simultaneamente a posição e o momento de um elétron (pode ser qualquer partícula). Há uma incerteza na posição\(\Delta x\) que é aproximadamente igual ao comprimento de onda da partícula. Ou seja,

\[\Delta x \approx \lambda.\]

Conforme discutido acima, uma onda não está localizada em um ponto no espaço. Se a posição do elétron for medida repetidamente, uma dispersão nas localizações será observada, o que implica uma incerteza na posição\(\Delta x\). Para detectar a posição da partícula, precisamos interagir com ela, como fazer com que ela colida com um detector. Na colisão, a partícula perderá impulso. Essa mudança no momento pode ser próxima de zero até o momento total da partícula,\(p = h/\lambda\). Não é possível dizer quanto impulso será transferido para um detector e, portanto\(\Delta p\), também há uma incerteza no momento. De fato, a incerteza no momento pode ser tão grande quanto o próprio momento, o que em forma de equação significa que

\[\Delta p \approx \dfrac{h}{\lambda}.\]

A incerteza na posição pode ser reduzida usando um elétron de menor comprimento de onda, uma vez que\(\Delta x \approx \lambda\). Mas encurtar o comprimento de onda aumenta a incerteza no momento, uma vez que\(\Delta p \approx h/\lambda\). Por outro lado, a incerteza no momento pode ser reduzida usando um elétron de comprimento de onda maior, mas isso aumenta a incerteza na posição. Matematicamente, você pode expressar essa compensação multiplicando as incertezas. O comprimento de onda é cancelado, saindo

\[\Delta x \Delta p \approx h.\]

Portanto, se uma incerteza for reduzida, a outra deve aumentar para que seu produto seja\(\approx h\).

Com o uso da matemática avançada, Heisenberg mostrou que o melhor que pode ser feito em uma medição simultânea de posição e momento é

\[\Delta x \Delta p \geq \dfrac{h}{4\pi}.\]

Isso é conhecido como princípio da incerteza de Heisenberg. É impossível medir a posição\(x\) e o momento\(p\) simultaneamente com as incertezas\(\Delta x\) e\(\Delta p\) que se multiplicam para serem menores que\(h/4\pi\). Nenhuma incerteza pode ser zero. Nenhuma incerteza pode se tornar pequena sem que a outra se torne grande. Um comprimento de onda pequeno permite uma medição precisa da posição, mas aumenta o momento da sonda até o ponto de perturbar ainda mais o momento de um sistema que está sendo medido. Por exemplo, se um elétron é disperso de um átomo e tem um comprimento de onda pequeno o suficiente para detectar a posição dos elétrons no átomo, seu momento pode expulsar os elétrons de suas órbitas de uma maneira que perde informações sobre seu movimento original. Portanto, é impossível seguir um elétron em sua órbita ao redor de um átomo. Se você medir a posição do elétron, você o encontrará em um local definido, mas o átomo será interrompido. Medições repetidas em átomos idênticos produzirão distribuições de probabilidade interessantes para elétrons ao redor do átomo, mas não produzirão informações de movimento. As distribuições de probabilidade são chamadas de nuvens de elétrons ou orbitais. As formas desses orbitais são frequentemente mostradas em textos gerais de química e são discutidas em The Wave Nature of Matter Causes Quantization.

Exemplo\(\PageIndex{1}\): Heisenberg Uncertainty Principle in Position and Momentum for an Atom

1. Se a posição de um elétron em um átomo for medida com uma precisão de 0,0100 nm, qual é a incerteza do elétron na velocidade?
2. Se o elétron tem essa velocidade, qual é sua energia cinética em eV?

Estratégia

A incerteza na posição é a precisão da medição, ou\(\Delta x = 0.0100 \, nm\). Assim, a menor incerteza no momento\(\Delta p\) pode ser calculada usando\(\Delta x \Delta p \geq h/4\pi\). Uma vez encontrada a incerteza no momento\(\Delta p\), a incerteza na velocidade pode ser encontrada em\(\Delta p = m\Delta v\).

Solução para (a)

Usando o sinal de igual no princípio da incerteza para expressar a incerteza mínima, temos

\[\Delta x \Delta p = \dfrac{h}{4\pi}.\]

Resolver\(\Delta p\) e substituir valores conhecidos dá

\[p = \dfrac{h}{4\pi \Delta x} = \dfrac{6.63 \times 10^{-34} \, J \cdot}{4 \pi (1.00 \times 10^{-11} \, m)} = 5.28 \times 10^{-24} \, kg \cdot m/s\]

Assim,

\[\Delta p = 5.28 \times 10^{-24} \, kg \cdot m/s = m\Delta v.\]

Resolver\(\Delta v\) e substituir a massa de um elétron dá

\[\Delta v = \dfrac{\Delta p}{m} = \dfrac{5.28 \times 10^{-24} \, kg \cdot m/s}{9.11 \times 10^{-31} \, kg} = 5.79 \times 10^6 \, m/s.\]

Solução para (b)

Embora grande, essa velocidade não é altamente relativista e, portanto, a energia cinética do elétron é

\[KE_e = \dfrac{1}{2} mv^2\]

\[= \dfrac{1}{2} (0.11 \times 10^{-31} \, kg)(5.79 \times 10^6 \, m/s)^2\]

\[= (1.53 \times 10^{-17} \, J)\left(\dfrac{1 \, eV}{1.60 \times 10^{-19} \, J}\right) = 95.5 \, eV.\]

Discussão

Como os átomos têm aproximadamente 0,1 nm de tamanho, saber a posição de um elétron a 0,0100 nm o localiza razoavelmente bem dentro do átomo. Isso seria como poder ver detalhes com um décimo do tamanho do átomo. Mas a consequente incerteza na velocidade é grande. Você certamente não poderia segui-lo muito bem se sua velocidade fosse tão incerta. Para ter uma ideia mais aprofundada de quão grande é a incerteza na velocidade, assumimos que a velocidade do elétron era igual à sua incerteza e descobrimos que isso dava uma energia cinética de 95,5 eV. Isso é significativamente maior do que a diferença de energia típica entre os níveis nos átomos (veja [link]), de modo que é impossível obter uma energia significativa para o elétron se soubermos sua posição, mesmo que moderadamente bem.

Por que não notamos o princípio da incerteza de Heisenberg na vida cotidiana? A resposta é que a constante de Planck é muito pequena. Assim, o limite inferior na incerteza de medir a posição e o momento de objetos grandes é insignificante. Podemos detectar a luz solar refletida de Júpiter e seguir o planeta em sua órbita ao redor do Sol. A luz solar refletida altera o momento de Júpiter e cria uma incerteza em seu momento, mas isso é totalmente insignificante em comparação com o enorme momento de Júpiter. O princípio da correspondência nos diz que as previsões da mecânica quântica se tornam indistinguíveis da física clássica para objetos grandes, o que é o caso aqui.

Incerteza de Heisenberg para energia e tempo

Existe outra forma do princípio da incerteza de Heisenberg para medições simultâneas de energia e tempo. Em forma de equação,

\[\Delta E \Delta t \geq \dfrac{h}{4\pi},\]

onde\(\Delta E\) está a incerteza na energia e\(\Delta t\), está a incerteza no tempo. Isso significa que, dentro de um intervalo de tempo\(\Delta t\), não é possível medir a energia com precisão — haverá uma incerteza\(\Delta E\) na medição. Para medir a energia com mais precisão (para\(\Delta E\) diminuir), devemos aumentar\(\Delta t\). Esse intervalo de tempo pode ser a quantidade de tempo que levamos para fazer a medição, ou pode ser a quantidade de tempo que um determinado estado existe, como no próximo exemplo.

Exemplo\(\PageIndex{2}\): Heisenberg Uncertainty Principle for Energy and Time for an Atom

Um átomo em estado excitado armazena energia temporariamente. Se a vida útil desse estado excitado for medida como sendo\(1.0 \times 10^{-10} \, s\),

qual é a incerteza mínima na energia do estado em eV?

Estratégia

A incerteza mínima na energia\(\Delta E\) é encontrada usando o sinal de igual\(\Delta E\Delta t \geq h/4\pi\) e corresponde a uma escolha razoável para a incerteza no tempo. A maior incerteza no tempo é a vida útil completa do estado de excitação, ou\(\Delta t = 1.0 \times 10^{-10} \, s\).

Solução

Resolver o princípio da incerteza\(\Delta E\) e substituir valores conhecidos dá

\[\Delta E = \dfrac{h}{4\pi \Delta t} = \dfrac{6.63 \times 10^{-34} \, J \cdot s}{4\pi (1.0 \times 10^{-10} \, s)} = 5.3 \times 10^{-25} \, J.\]

Agora, convertendo para rendimentos de eV

\[\Delta E = (5.3 \times 10^{-25} \, J) \left( \dfrac{1 \, eV}{1.6 \times 10^{-19} \, J} \right) = 3.3 \times 10^{-6} \, eV.\]

Discussão

A vida útil de\(10^{-10} \, s\) é típica de estados excitados em átomos — em escalas de tempo humanas, eles emitem rapidamente a energia armazenada. Uma incerteza na energia de apenas alguns milionésimos de um eV resulta. Essa incerteza é pequena em comparação com as energias de excitação típicas nos átomos, que são da ordem de 1 eV. Então, aqui, o princípio da incerteza limita a precisão com a qual podemos medir a vida útil e a energia de tais estados, mas não de forma muito significativa.

O princípio da incerteza para energia e tempo pode ser de grande importância se a vida útil de um sistema for muito curta. Então\(\Delta t\) é muito pequeno e\(\Delta E\), consequentemente, muito grande. Alguns núcleos e partículas exóticas têm uma vida útil extremamente curta (tão pequena quanto\(10^{-25} \, s\)), causando incertezas de energia tão grandes quanto muitos GeV\(10^9 \, eV\). A energia armazenada aparece como aumento da massa de repouso e, portanto, isso significa que há uma incerteza significativa na massa restante de partículas de vida curta. Quando medido repetidamente, obtém-se uma dispersão de massas ou energias de decaimento. O spread é\(\Delta E\). Você pode perguntar se essa incerteza na energia poderia ser evitada ao não medir a vida útil. A resposta é não. A natureza conhece a vida e, portanto, sua brevidade afeta a energia da partícula. Isso está tão bem estabelecido experimentalmente que a incerteza na energia de decaimento é usada para calcular a vida útil de estados de vida curta. Alguns núcleos e partículas têm vida tão curta que é difícil medir sua vida útil. Mas se sua energia de decaimento pode ser medida, sua dispersão é\(\Delta E\) e isso é usado no princípio da incerteza\((\Delta E \Delta t \geq h/4\pi)\) para calcular a vida útil\(\Delta t\).

Há outra consequência do princípio da incerteza para energia e tempo. Se a energia for incerta por\(\Delta E\), a conservação da energia pode ser violada\(\Delta E\) por um tempo\(\Delta t\). Nem o físico nem a natureza podem dizer que a conservação de energia foi violada, se a violação for temporária e menor do que a incerteza da energia. Embora isso pareça inócuo o suficiente, veremos nos capítulos posteriores que ele permite a criação temporária de matéria do nada e tem implicações na forma como a natureza transmite forças em distâncias muito pequenas.

Por fim, observe que, na discussão sobre partículas e ondas, afirmamos que medições individuais produzem resultados precisos ou semelhantes a partículas. Uma posição definida é determinada cada vez que observamos um elétron, por exemplo. Mas medições repetidas produzem uma dispersão nos valores consistente com as características da onda. O grande físico teórico Richard Feynman (1918—1988) comentou: “O que existem são partículas”. Quando você observa um número suficiente deles, eles se distribuem como seria de esperar de um fenômeno de onda. No entanto, o que há quando viajam, não podemos dizer porque, quando tentamos medir, afetamos a viagem.

Resumo

• Verificou-se que a matéria tem as mesmas características de interferência de qualquer outra onda.
• Agora existe uma distribuição de probabilidade para a localização de uma partícula em vez de uma posição definida.
• Outra consequência do caráter ondulatório de todas as partículas é o princípio da incerteza de Heisenberg, que limita a precisão com a qual certas quantidades físicas podem ser conhecidas simultaneamente. Para posição e momentum, o princípio da incerteza é\(\Delta x \Delta p \geq \frac{h}{4 \pi}\): onde\(\Delta x\) está a incerteza na posição e\(\Delta p\) é a incerteza no momento.
• Para energia e tempo, o princípio da incerteza é\(\Delta E \Delta t \geq \frac{h}{4 \pi}\): onde\(\Delta E\) está a incerteza na energia e\(\Delta t\) é a incerteza no tempo.
• Esses pequenos limites são fundamentalmente importantes na escala de mecânica quântica.

Glossário

Princípio da incerteza de Heisenberg

um limite fundamental para a precisão com a qual pares de quantidades (momento e posição, energia e tempo) podem ser medidos

incerteza na energia

falta de precisão ou falta de conhecimento de resultados precisos em medições de energia

incerteza no tempo

falta de precisão ou falta de conhecimento de resultados precisos em medições de tempo

incerteza no momentum

falta de precisão ou falta de conhecimento de resultados precisos em medições de momento

incerteza na posição

falta de precisão ou falta de conhecimento de resultados precisos em medições de posição

distribuição de probabilidade

a distribuição espacial geral das probabilidades de encontrar uma partícula em um determinado local