28.2: Simultaneidade e dilatação do tempo

Objetivos de

Ao final desta seção, você poderá:

• Descreva a simultaneidade.
• Descreva a dilatação temporal.
• Calcule γ.
• Compare o tempo adequado e o tempo medido pelo observador.
• Explique por que o paradoxo dos gêmeos é um falso paradoxo.

Os intervalos de tempo dependem de quem os observa? Intuitivamente, esperamos que o tempo necessário para um processo, como o tempo decorrido para uma corrida a pé, seja o mesmo para todos os observadores. Nossa experiência mostra que divergências sobre o tempo decorrido têm a ver com a precisão da medição do tempo. Quando consideramos cuidadosamente como o tempo é medido, no entanto, descobriremos que o tempo decorrido depende do movimento relativo de um observador em relação ao processo que está sendo medido.

Figura\(\PageIndex{1}\): O tempo decorrido para uma corrida a pé é o mesmo para todos os observadores, mas em velocidades relativistas, o tempo decorrido depende do movimento relativo do observador e do evento observado. (crédito: Jason Edward Scott Bain, Flickr)

Simultaneidade

Considere como medimos o tempo decorrido. Se usarmos um cronômetro, por exemplo, como sabemos quando ligar e parar o relógio? Um método é usar a chegada da luz do evento, como observar uma luz ficando verde para iniciar uma corrida de arrancada. O tempo será mais preciso se algum tipo de detecção eletrônica for usado, evitando tempos de reação humana e outras complicações.

Agora, suponha que usemos esse método para medir o intervalo de tempo entre dois flashes de luz produzidos por lâmpadas de flash (Figura\(\PageIndex{2}\)). Duas lâmpadas de flash com o observador A a meio caminho entre elas estão em um vagão que se move para a direita em relação ao observador B. O observador B organiza para que os flashes de luz sejam emitidos assim como A passa por B, de forma que A e B fiquem equidistantes das lâmpadas quando a luz é emitida. O observador B mede o intervalo de tempo entre a chegada dos flashes de luz. De acordo com o postulado 2, a velocidade da luz não é afetada pelo movimento das lâmpadas em relação a B. Portanto, a luz viaja distâncias iguais até ele em velocidades iguais. Assim, o observador B mede que os flashes sejam simultâneos.

Figura\(\PageIndex{2}\): O observador B mede o tempo decorrido entre a chegada dos flashes de luz, conforme descrito no texto. O observador A se move com as lâmpadas de um vagão. O observador B vê os flashes de luz que ocorrem simultaneamente. O observador B vê a luz à direita alcançando o observador A antes da luz à esquerda.

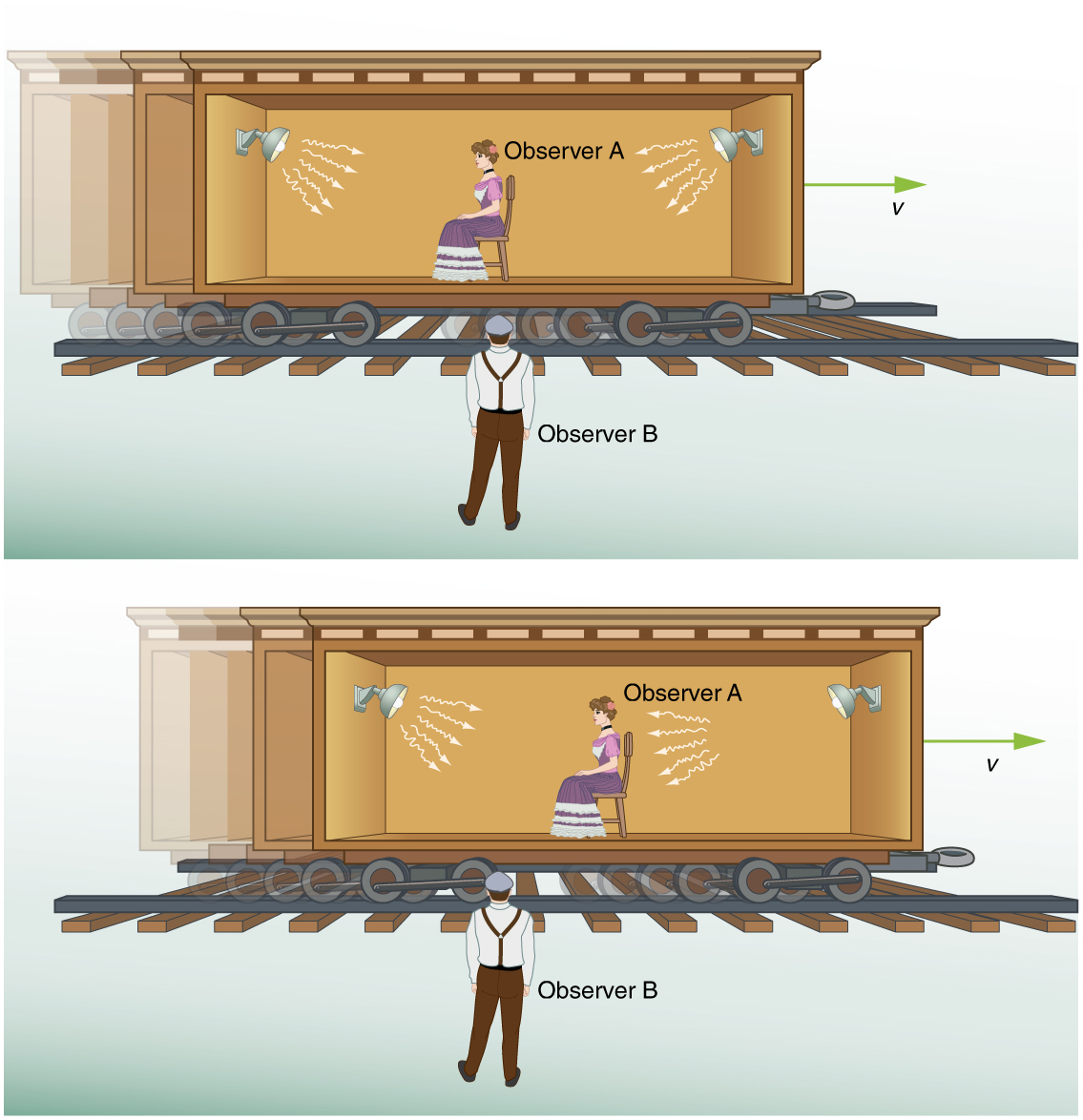
Agora, considere o que o observador B vê acontecer com o observador A. O observador B vê a luz da direita alcançando o observador A antes da luz da esquerda, porque ela se moveu em direção a essa lâmpada de flash, diminuindo a distância que a luz deve percorrer e reduzindo o tempo necessário para chegar até ela. A luz viaja em velocidade em\(c\) relação a ambos os observadores, mas o observador B permanece equidistante entre os pontos onde os flashes foram emitidos, enquanto A se aproxima do ponto de emissão à direita. Do ponto de vista do observador B, então, há um intervalo de tempo entre a chegada dos flashes ao observador A. O observador B mede os flashes para chegar simultaneamente em relação a ele, mas não em relação a A.

Agora, considere o que o observador A vê acontecendo. Ela vê a luz da direita ao mesmo tempo que vê a luz da esquerda. Como as duas lâmpadas estão à mesma distância dela em seu quadro de referência, do ponto de vista dela, os flashes ocorreram ao mesmo tempo. Aqui, uma velocidade relativa entre observadores afeta se dois eventos são observados como simultâneos.

A simultaneidade não é absoluta.

Isso ilustra o poder do pensamento claro. Podemos ter adivinhado incorretamente que, se a luz fosse emitida simultaneamente, dois observadores a meio caminho entre as fontes veriam os flashes simultaneamente. Mas uma análise cuidadosa mostra que esse não é o caso. Einstein foi brilhante nesse tipo de experimento mental (em alemão, “Gedankenexperiment”). Ele considerou cuidadosamente como uma observação é feita e desconsiderou o que poderia parecer óbvio. A validade dos experimentos mentais, é claro, é determinada pela observação real. A genialidade de Einstein é evidenciada pelo fato de que experimentos confirmaram repetidamente sua teoria da relatividade.

Em resumo: dois eventos são definidos como simultâneos se um observador os medir como ocorrendo ao mesmo tempo (por exemplo, ao receber luz dos eventos). Dois eventos não são necessariamente simultâneos para todos os observadores.

Dilatação do tempo

A consideração da medição do tempo decorrido e da simultaneidade leva a um importante efeito relativista.

Definição: Dilatação do tempo

A dilatação do tempo é o fenômeno do tempo passar mais devagar para um observador que está se movendo em relação a outro observador.

Suponha, por exemplo, que uma astronauta meça o tempo que a luz leva para cruzar sua nave, ricochetear em um espelho e retornar (Figura\(\PageIndex{3}\)). Como o tempo decorrido medido pelo astronauta se compara ao tempo decorrido medido para o mesmo evento por uma pessoa na Terra? Fazer essa pergunta (outro experimento mental) produz um resultado profundo. Descobrimos que o tempo decorrido para um processo depende de quem o está medindo. Nesse caso, o tempo medido pelo astronauta é menor do que o tempo medido pelo observador terrestre. A passagem do tempo é diferente para os observadores porque a distância que a luz percorre no quadro do astronauta é menor do que na estrutura terrestre. A luz viaja na mesma velocidade em cada quadro e, portanto, levará mais tempo para percorrer a maior distância na estrutura ligada à Terra.

Figura\(\PageIndex{3}\): (a) Uma astronauta mede o tempo até\(\Delta t_{0}\) a luz cruzar sua nave usando um cronômetro eletrônico. A luz percorre uma distância\(2D\) na estrutura do astronauta. (b) Uma pessoa na Terra vê a luz seguir o caminho mais longo\(2s\) e demorar mais tempo\(\Delta t\). (c) Esses triângulos são usados para encontrar a relação entre as duas distâncias\(2D\)\(2s\) e.

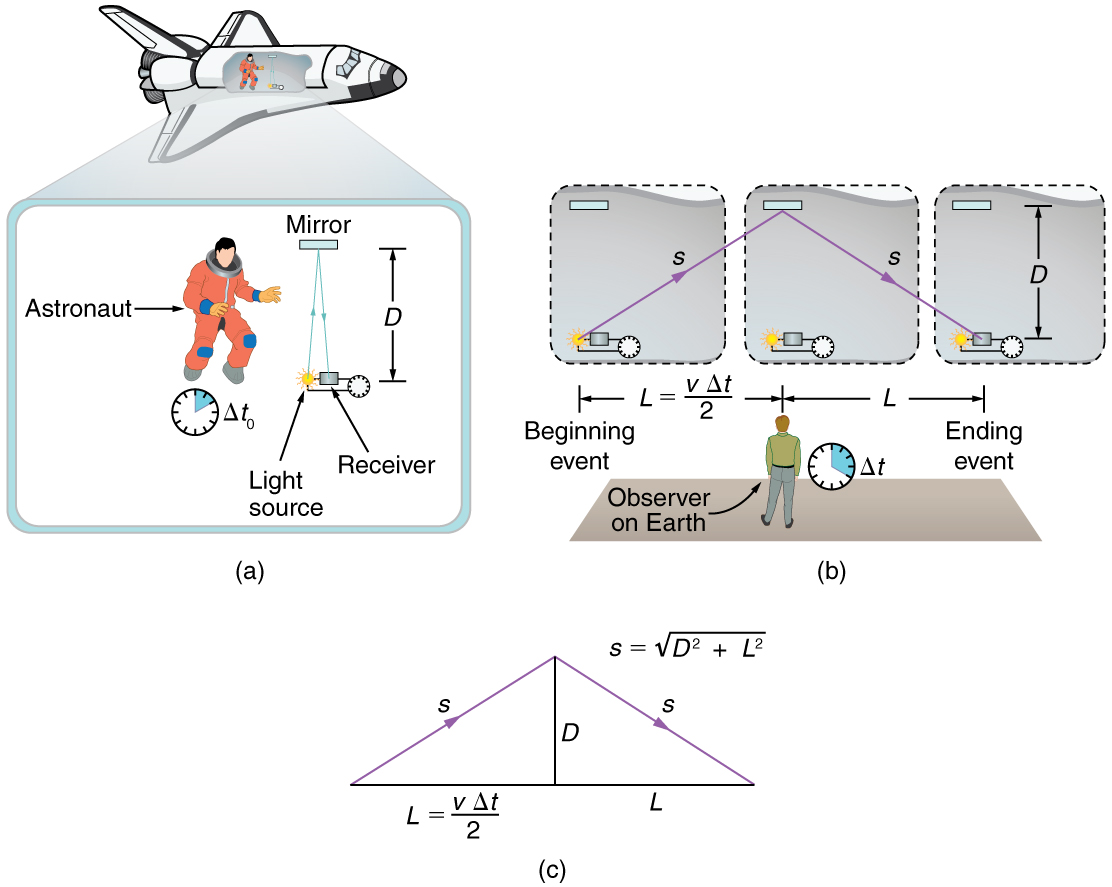
Para verificar quantitativamente que o tempo depende do observador, considere os caminhos seguidos pela luz vistos por cada observador (Figura\(\PageIndex{3c}\)). A astronauta vê a luz viajar de um lado para o outro por uma distância total de\(2D\), duas vezes a largura de sua nave. O observador terrestre vê a luz percorrer uma distância total\(2s\). Como a nave está se movendo em velocidade\(v\) para a direita em relação à Terra, a luz que se move para a direita atinge o espelho nessa moldura. A luz viaja a uma velocidade\(c\) em ambos os quadros, e porque o tempo é a distância dividida pela velocidade, o tempo medido pelo astronauta é\[\Delta t_{0} = \frac{2D}{c}.\label{28.3.1}\] Este tempo tem um nome separado para distingui-lo do tempo medido pelo observador terrestre.

Definição: Tempo adequado

O tempo adequado\(\Delta t_{0}\) é o tempo medido por um observador em repouso em relação ao evento que está sendo observado.

No caso do astronauta observar a luz refletida, o astronauta mede o tempo adequado. O tempo medido pelo observador ligado à Terra é

\[\Delta t = \frac{2s}{c}\label{28.3.2}. \nonumber\]

Para encontrar a relação entre\(\Delta t_{0}\) e\(\Delta t\), considere os triângulos formados por\(D\) e\(s\) (Figura\(\PageIndex{3c}\).) O terceiro lado desses triângulos semelhantes é\(L\) a distância que a astronauta se move à medida que a luz atravessa sua nave. No quadro do observador ligado à Terra,

\[L = \frac{v\Delta t}{2}\label{28.3.3}. \nonumber\]

Usando o Teorema de Pitágoras, descobriu-se\(s\) que a distância é

\[s = \sqrt{D^{2} + \left(\dfrac{v\Delta t}{2} \right) ^{2}}.\label{28.3.4} \nonumber\]

\(s\)Substituindo o intervalo de tempo na expressão,\(\Delta t\) obtém-se

\[\Delta t = \dfrac{2s}{c} = \dfrac{2 \sqrt{D^{2} + \left( \dfrac{v\Delta t}{2} \right) ^{2}}}{c}.\label{28.3.5} \nonumber\]

Fazemos o quadrado dessa equação, que produz

\[\begin{align*} (\Delta t)^2 &= \dfrac{4\left(D^2 + \dfrac{v^2(\Delta t)^2}{4}\right)}{c^2} \\[4pt] &= \dfrac{4D^2}{c^2} + \dfrac{v^2}{c^2}(\Delta t)^2. \end{align*}\]

Observe que, se colocarmos ao quadrado a primeira expressão que tínhamos,\(\Delta t_0\) obteremos\((\Delta t_0)^2 = \frac{4D^2}{c^2}\). Esse termo aparece na equação anterior, nos dando um meio de relacionar os dois intervalos de tempo. Assim,

\[(\Delta t)^2 = (\Delta t_0)^2 + \dfrac{v^2}{c^2}(\Delta t)^2. \nonumber\]

Reunindo termos, resolvemos\(\Delta t\):

\[(\Delta t)^2 \left(1 - \dfrac{v^2}{c^2}\right) = (\Delta t_0)^2. \nonumber\]

Assim,

\[(\Delta t)^2 = \dfrac{(\Delta t_0)^2}{1 - \dfrac{v^2}{c^2}}. \nonumber\]

Tomar a raiz quadrada produz uma relação importante entre os tempos decorridos:

\[\begin{align*} \Delta t &= \dfrac{\Delta t_0}{\sqrt{1 - \frac{v^2}{c^2}}} \\[4pt] &= \gamma \Delta t_0, \end{align*}\]

onde

\[\gamma = \dfrac{1}{\sqrt{1 - \frac{v^2}{c^2}}}. \nonumber\]

Essa equação para\(\Delta t\) é realmente notável. Primeiro, como afirmado, o tempo decorrido não é o mesmo para diferentes observadores que se movem em relação um ao outro, mesmo que ambos estejam em quadros inerciais. O tempo adequado\(\Delta t\) medido por um observador, como o astronauta se movendo com o aparelho, é menor do que o tempo medido por outros observadores. Como esses outros observadores medem mais tempo\(\Delta t\), o efeito é chamado de dilatação do tempo. O observador ligado à Terra vê o tempo se dilatar (ficar mais longo) para um sistema se movendo em relação à Terra. Como alternativa, de acordo com o observador terrestre, o tempo diminui na estrutura móvel, pois menos tempo passa lá. Observa-se que todos os relógios que se movem em relação a um observador, incluindo relógios biológicos, como o envelhecimento, funcionam lentamente em comparação com um relógio estacionário em relação ao observador.

Observe que se a velocidade relativa for muito menor que a velocidade da luz\((v \ll c)\), então\(\frac{v^2}{c^2}\) é extremamente pequena e os tempos\(\Delta t\) decorridos\(\Delta t_0\) são quase iguais. Em baixas velocidades, a relatividade moderna se aproxima da física clássica — nossas experiências cotidianas têm efeitos relativistas muito pequenos.

A equação\(\Delta t = \gamma \delta t_0\) também implica que a velocidade relativa não pode exceder a velocidade da luz. À medida que\(v\) se aproxima\(c\),\(\Delta t\) também implica que a velocidade relativa não pode exceder a velocidade da luz. Quando\(v\) excedido\(c\), então estaríamos tomando a raiz quadrada de um número negativo, produzindo um valor imaginário para\(\Delta t\).

Há evidências experimentais consideráveis de que a equação\(\delta t = \gamma \Delta t_0\) está correta. Um exemplo é encontrado em partículas de raios cósmicos que chovem continuamente sobre a Terra a partir do espaço profundo. Algumas colisões dessas partículas com núcleos na alta atmosfera resultam em partículas de vida curta chamadas múons. A meia-vida (quantidade de tempo para a metade de um material se decompor) de um múon é\(1.52 \, \mu s\) quando ele está em repouso em relação ao observador que mede a meia-vida. Essa é a hora certa\(\Delta t_0\). Os múons produzidos por partículas de raios cósmicos têm uma faixa de velocidades, com alguns se movendo perto da velocidade da luz. Foi descoberto que a meia-vida do múon medida por um observador ligado à Terra\((\Delta t)\) varia com a velocidade exatamente como previsto pela equação\(\delta t = \gamma \Delta t_0\). Quanto mais rápido o múon se move, mais ele vive. Nós, na Terra, vemos o tempo de meia-vida do múon dilatado - como visto de nossa estrutura, o múon decai mais lentamente do que quando está em repouso em relação a nós.

Exemplo\(\PageIndex{1}\): Calculating \(\Delta t\) for a Relativistic Event: How Long Does a Speedy Muon Live?

Suponha que um raio cósmico colidindo com um núcleo na alta atmosfera da Terra produza um múon que tenha uma velocidade\(v = 0.950 \, c\). O múon então viaja a uma velocidade constante e vive\(1.52 \, \mu s\) conforme medido no quadro de referência do múon. (Você pode imaginar isso como o relógio interno do múon.) Quanto tempo o múon vive conforme medido por um observador ligado à Terra (Figura\(\PageIndex{4}\))?

Figura\(\PageIndex{4}\): Um múon na atmosfera da Terra vive mais tempo medido por um observador ligado à Terra do que medido pelo relógio interno do múon.

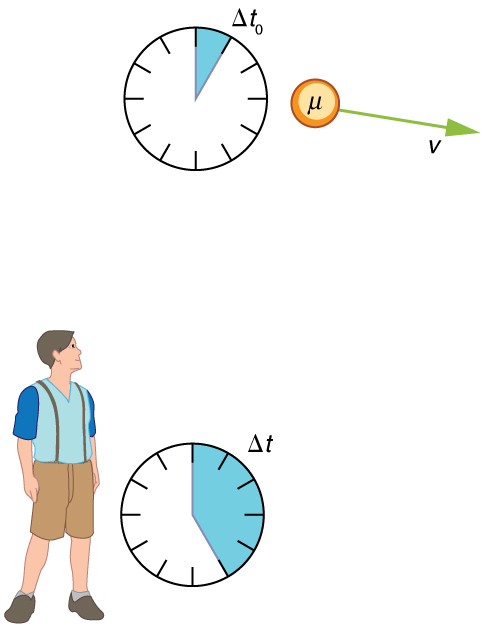
Estratégia

Um relógio em movimento com o sistema sendo medido observa a hora correta, então a hora que nos é dada é\(\Delta t_0 = 1.52 \, \mu s\). O observador ligado à Terra mede\(\Delta t\) conforme dado pela equação\(\delta t = \gamma \Delta t_0\).

Como sabemos a velocidade, o cálculo é simples.

Solução

1. Identifique os conhecidos. \(v = 0.950c\),\(\Delta t_{0} = 1.52 \mu s\)
2. Identifique o desconhecido. \(\Delta t\)
3. Escolha a equação apropriada.
   Use,\[\Delta t = \gamma \Delta t_{0},\label{28.3.6} \nonumber\] onde\[\gamma = \frac{1}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}.\nonumber\]
4. Insira os conhecidos na equação.
   Primeira descoberta\(\gamma\). \[\begin{align*} \gamma &= \frac{1}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} \\[4pt] &= \frac{1}{\sqrt{1 - \frac{\left(0.950\right)^{2}}{c^{2}}}} \\[4pt] &= \frac{1}{\sqrt{1 - \left(0.950\right)^{2}}} \\[4pt] &= 3.20. \end{align*}\]
   Use o valor calculado de\(\gamma\) para determinar\(\Delta t\).
   \[\begin{align*} \Delta t &= \gamma \Delta t_{0} \\[4pt] &= \left(3.20\right)\left(1.52 \mu s\right) \\[4pt] &= 4.87 \mu s \end{align*}\]

Discussão

Uma implicação desse exemplo é que, como\(\gamma = 3.20\) na velocidade\(95.0\%\) da luz (\(v = 0.950c\)), os efeitos relativísticos são significativos. Os dois intervalos de tempo diferem por esse fator de 3,20, onde classicamente seriam os mesmos. Diz-se que algo\(0.950 c\) está se movendo é altamente relativista.

Outra implicação do exemplo anterior é que tudo o que um astronauta faz quando se move à velocidade\(95.0\%\) da luz em relação à Terra leva 3,20 vezes mais tempo quando observado da Terra. O astronauta sente isso? Só se ela olhar para fora de sua nave espacial. Todos os métodos de medição do tempo em seu quadro serão afetados pelo mesmo fator de 3,20. Isso inclui seu relógio de pulso, frequência cardíaca, taxa de metabolismo celular, taxa de impulso nervoso e assim por diante. Ela não terá como saber, já que todos os seus relógios concordarão um com o outro porque suas velocidades relativas são zero. O movimento é relativo, não absoluto. Mas e se ela olhar pela janela?

Conexões do mundo real

Pode parecer que a relatividade especial tem pouco efeito em sua vida, mas provavelmente é mais importante do que você imagina. Um dos efeitos mais comuns é por meio do Sistema de Posicionamento Global (GPS). Veículos de emergência, serviços de entrega de pacotes, mapas eletrônicos e dispositivos de comunicação são apenas alguns dos usos comuns do GPS, e o sistema GPS não poderia funcionar sem levar em conta os efeitos relativísticos. Os satélites GPS dependem de medições de tempo precisas para se comunicar. Os sinais viajam em velocidades relativistas. Sem correções na dilatação do tempo, os satélites não conseguiam se comunicar e o sistema GPS falharia em minutos.

O paradoxo dos gêmeos

Uma consequência intrigante da dilatação do tempo é que um viajante espacial se movendo a uma alta velocidade em relação à Terra envelheceria menos do que seu gêmeo ligado à Terra. Imagine o astronauta se movendo a uma velocidade\(\gamma = 30.0\) como na Figura\(\PageIndex{5}\). Uma viagem que leva 2,00 anos em seu corpo levaria 60,0 anos no quadro de sua irmã gêmea ligada à Terra. Suponha que o astronauta tenha viajado 1,00 ano para outro sistema estelar. Ela explorou brevemente a área e depois viajou 1,00 ano atrás. Se a astronauta tivesse 40 anos quando partiu, ela teria 42 anos ao retornar. Tudo na Terra, no entanto, teria envelhecido 60,0 anos. Seu irmão gêmeo, se ainda estivesse vivo, teria 100 anos.

A situação pareceria diferente para o astronauta. Como o movimento é relativo, a espaçonave parece estar estacionária e a Terra parece se mover. (Essa é a sensação que você tem ao voar em um jato.) Se a astronauta olhar pela janela da nave espacial, ela verá o tempo desacelerar na Terra por um fator de\(\gamma = 30.0\). Para ela, a irmã ligada à Terra terá envelhecido apenas 2/30 (1/15) de um ano, enquanto ela tinha 2,00 anos. As duas irmãs não podem estar corretas.

Figura\(\PageIndex{5}\): O paradoxo dos gêmeos pergunta por que os gêmeos viajantes envelhecem menos do que os gêmeos que estão na Terra. Essa é a previsão que obtemos se considerarmos a estrutura do gêmeo ligado à Terra. No quadro do astronauta, no entanto, a Terra está se movendo e o tempo corre mais devagar lá. Quem está correto?

Como em todos os paradoxos, a premissa é falsa e leva a conclusões contraditórias. Na verdade, o movimento do astronauta é significativamente diferente daquele do gêmeo ligado à Terra. O astronauta acelera até uma alta velocidade e depois desacelera para ver o sistema estelar. Para retornar à Terra, ela novamente acelera e desacelera. O gêmeo ligado à Terra não experimenta essas acelerações. Portanto, a situação não é simétrica e não é correto afirmar que a astronauta observará os mesmos efeitos de sua irmã gêmea ligada à Terra. Se você usar a relatividade especial para examinar o paradoxo dos gêmeos, lembre-se de que a teoria é expressamente baseada em quadros inerciais, que por definição não são acelerados ou giratórios. Einstein desenvolveu a relatividade geral para lidar com quadros acelerados e com a gravidade, a principal fonte de aceleração. Você também pode usar a relatividade geral para abordar o paradoxo dos gêmeos e, de acordo com a relatividade geral, o astronauta envelhecerá menos. Alguns aspectos conceituais importantes da relatividade geral são discutidos na Seção sobre Relatividade Geral e Gravidade Quântica deste curso.

Em 1971, os físicos americanos Joseph Hafele e Richard Keating verificaram a dilatação do tempo em baixas velocidades relativas voando relógios atômicos extremamente precisos ao redor da Terra em aeronaves comerciais. Eles mediram o tempo decorrido com uma precisão de alguns nanossegundos e o compararam com o tempo medido pelos relógios deixados para trás. Os resultados de Hafele e Keating estavam dentro das incertezas experimentais das previsões da relatividade. Tanto a relatividade especial quanto a geral tiveram que ser levadas em consideração, pois a gravidade e as acelerações estavam envolvidas, bem como o movimento relativo.

Exercício\(\PageIndex{1}\)

1. O que é\(\gamma\) se\(v = 0.650 c\)?
2. Uma partícula viaja\(1.90 \times 10^8 \, m/s\) e vive\(2.10 \times 10^{-8} s\) quando está em repouso em relação a um observador. Por quanto tempo a partícula vive conforme vista em laboratório?

Responda

1. \(\gamma = \dfrac{1}{\sqrt{1 - \frac{v^2}{e^2}}} = \dfrac{1}{\sqrt{1 - \frac{(0.650 c)^2}{c^2}}} = 1.32\)
2. \(\Delta t = \dfrac{\Delta_t^0}{\sqrt{1-\frac{v^2}{c^2}}} = \dfrac{2.10 \times 10^{-8} s}{\sqrt{1 - \frac{(1.90 \times 10^8 \, m/s)^2}{(3.00 \times 10^8 \, m/s)^2}}} = 2.71 \times 10^{-8} \, s\)

Resumo

• Dois eventos são definidos como simultâneos se um observador os medir como ocorrendo ao mesmo tempo. Eles não são necessariamente simultâneos para todos os observadores — a simultaneidade não é absoluta.
• A dilatação do tempo é o fenômeno do tempo passar mais devagar para um observador que está se movendo em relação a outro observador.
• Observadores que se movem a uma velocidade relativa\(v\) não medem o mesmo tempo decorrido para um evento. O tempo adequado\(\Delta t_0\) é o tempo medido por um observador em repouso em relação ao evento que está sendo observado. O tempo adequado está relacionado ao tempo\(\Delta t\) medido por um observador ligado à Terra pela equação\[\Delta t = \dfrac{\Delta t_0}{\sqrt{1 - \frac{v^2}{c^2}}} = \gamma \Delta t_0, \nonumber \] em que\[\gamma = \dfrac{1}{\sqrt{1 - \frac{v^2}{c^2}}}. \nonumber \]
• A equação que relaciona o tempo e o tempo adequados medidos por um observador ligado à Terra implica que a velocidade relativa não pode exceder a velocidade da luz.
• O paradoxo dos gêmeos pergunta por que um gêmeo viajando a uma velocidade relativista e depois voltando para a Terra envelhece menos do que o gêmeo ligado à Terra. A premissa do paradoxo é falsa porque o gêmeo viajante está acelerando. A relatividade especial não se aplica a quadros de referência acelerados.
• A dilatação do tempo geralmente é insignificante em baixas velocidades relativas, mas ocorre e foi verificada por experimentos.

Glossário

dilatação do tempo

o fenômeno do tempo passar mais devagar para um observador que está se movendo em relação a outro observador

tempo adequado

\(\Delta t_0\)o tempo medido por um observador em repouso em relação ao evento observado:\(\Delta t = \dfrac{\Delta t_0}{\sqrt{1 - \frac{v^2}{c^2}}} = \gamma \Delta t_0,\) onde\(\gamma = \dfrac{1}{\sqrt{1 - \frac{v^2}{c^2}}}\)

paradoxo dos gêmeos

isso pergunta por que um gêmeo viajando a uma velocidade relativista e depois voltando para a Terra tem menos idade do que o gêmeo ligado à Terra. A premissa do paradoxo é defeituosa porque o gêmeo viajante está acelerando e a relatividade especial não se aplica aos quadros de referência acelerados.