Skip to main content
Global

28.3: Contração do comprimento

  1. Last updated
  2. Save as PDF
  • Page ID
    194175

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Descreva o comprimento adequado.
    • Calcule a contração do comprimento.
    • Explique por que não notamos esses efeitos em escalas diárias.

    Você já dirigiu em uma estrada que parece durar para sempre? Se você olhar para frente, você pode dizer que ainda tem cerca de 10 km pela frente. Outro viajante pode dizer que a estrada à frente parece ter cerca de 15 km de extensão. Se vocês dois medissem a estrada, no entanto, concordariam. Viajando em velocidades diárias, a distância que vocês dois medem seria a mesma. Você lerá nesta seção, no entanto, que isso não é verdade em velocidades relativistas. Perto da velocidade da luz, as distâncias medidas não são as mesmas quando medidas por observadores diferentes.

    Uma longa estrada isolada de pista dupla banhada por terrenos áridos em ambos os lados.
    Figura\(\PageIndex{1}\): As pessoas podem descrever as distâncias de forma diferente, mas em velocidades relativistas, as distâncias são realmente diferentes. (crédito: Corey Leopold, Flickr)

    Comprimento adequado

    Uma coisa com a qual todos os observadores concordam é a velocidade relativa. Embora os relógios meçam diferentes tempos decorridos para o mesmo processo, eles ainda concordam que a velocidade relativa, que é a distância dividida pelo tempo decorrido, é a mesma. Isso implica que a distância também depende do movimento relativo do observador. Se dois observadores virem horários diferentes, eles também devem ver distâncias diferentes para que a velocidade relativa seja a mesma para cada um deles.

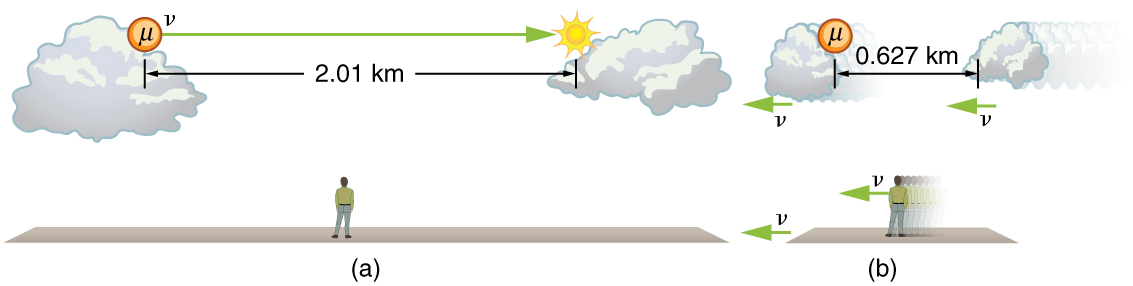
    O múon[1] ilustra esse conceito. Para um observador na Terra, o múon viaja em ou\(7.05 \mu s\) desde o momento em que é produzido até se\(0.950c\) decompor. Assim, ele viaja uma distância\[L_{0} = v \Delta t = \left(0.950\right)\left(3.00 \times 10^{8} m/s\right)\left(7.05 \times 10^{-6} s\right) = 2.01 km \label{28.4.1}\] em relação à Terra. No quadro de referência do múon, sua vida útil é apenas\(2.20 \mu s\). Tem tempo suficiente para viajar apenas.\[L = v \Delta t_{0} = \left(0.950\right)\left(3.00 \times 10^{8} m/s\right)\left(2.20 \times 10^{-6} s\right) = 0.627 km. \label{28.4.2}\] A distância entre os mesmos dois eventos (produção e decaimento de um múon) depende de quem o mede e como eles estão se movendo em relação a ele.

    COMPRIMENTO ADEQUADO

    O comprimento adequado\(L_{0}\) é a distância entre dois pontos medida por um observador que está em repouso em relação a ambos os pontos.

    O observador ligado à Terra mede o comprimento adequado\(L_{0}\), porque os pontos em que o múon é produzido e decai são estacionários em relação à Terra. Para o múon, a Terra, o ar e as nuvens estão se movendo e, portanto, a distância\(L\) que ele vê não é o comprimento adequado.

    Em parte, um observador observa da estrutura de referência terrestre um múon acima da terra com velocidade v na direção direita. A distância entre o múon e o local onde ele se desintegra é de dois pontos zero um. Na parte b, o sistema é mostrado em movimento com a velocidade v na direção esquerda. Então, a nuvem e o solo são deslocados zero ponto seis dois sete quilos metros na direção oposta.
    Figura\(\PageIndex{2}\): (a) O observador ligado à Terra vê o múon viajar 2,01 km entre as nuvens. (b) O múon se vê percorrendo o mesmo caminho, mas apenas a uma distância de 0,627 km. A Terra, o ar e as nuvens estão se movendo em relação ao múon em sua estrutura, e todos parecem ter comprimentos menores ao longo da direção da viagem.

    Contração do comprimento

    Para desenvolver uma equação relacionando distâncias medidas por diferentes observadores, notamos que a velocidade relativa ao observador ligado à Terra em nosso exemplo de múon é dada por\[v = \frac{L_{0}}{\Delta t}.\label{28.4.3}\] O tempo relativo ao observador ligado à Terra é\(\Delta t\), uma vez que o objeto que está sendo cronometrado está se movendo em relação a esse observador. A velocidade relativa ao observador em movimento é dada por\[v = \frac{L}{\Delta t_{0}}.\label{28.4.4}\] O observador em movimento viaja com o múon e, portanto, observa o tempo adequado\(\Delta t_{0}\). As duas velocidades são idênticas; portanto,\[\frac{L_{0}}{\Delta t} = \frac{L}{\Delta t_{0}}.\label{28..4.5}\] sabemos disso\(\Delta t = \gamma \Delta t_{0}\). Substituindo essa equação na relação acima,\[L = \frac{L_{0}}{\gamma}.\label{28.4.6}\] Substituindo por\(\gamma\) fornece uma equação que relaciona as distâncias medidas por diferentes observadores.

    CONTRAÇÃO DO COMPRIMENTO

    A contração do comprimento\(L\) é o encurtamento do comprimento medido de um objeto em movimento em relação à moldura do observador. \[L = L_{0} \sqrt{1-\frac{v^{2}}{c^{2}}}.\label{28.4.7}\]

    Se medirmos o comprimento de qualquer coisa que se move em relação à nossa estrutura, descobrimos que seu comprimento\(L\) é menor do que o comprimento adequado\(L_{0}\) que seria medido se o objeto estivesse parado. Por exemplo, no quadro de referência do múon, a distância entre os pontos onde ele foi produzido e onde ele se decompôs é menor. Esses pontos são fixos em relação à Terra, mas se movem em relação ao múon. Nuvens e outros objetos também são contraídos ao longo da direção do movimento no quadro de referência do múon.

    Exemplo\(\PageIndex{1}\): Calculating Length Contraction: The Distance between Stars Contracts when You Travel at High Velocity:

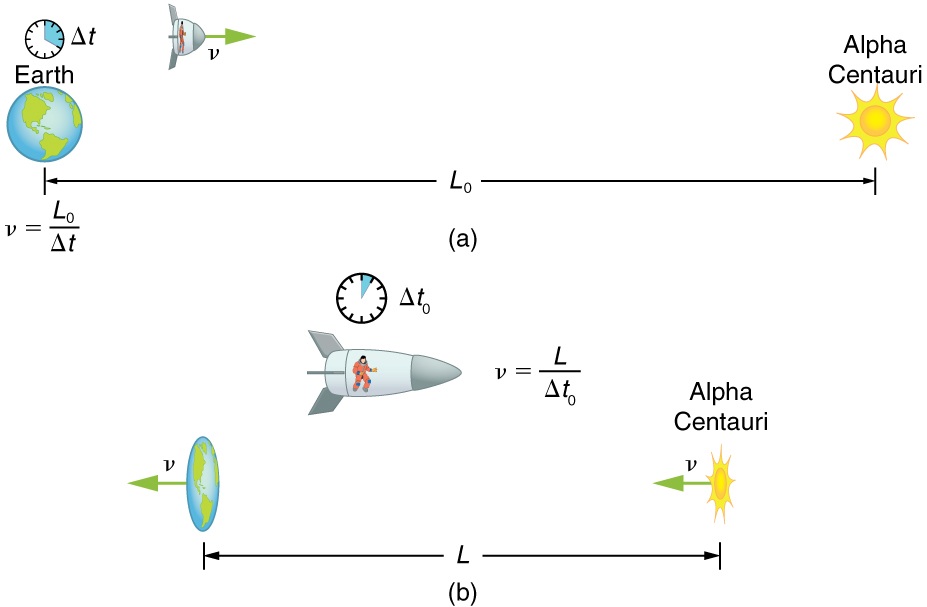
    Suponha que um astronauta, como o gêmeo discutido em “Simultaneidade e dilatação do tempo”, viaje tão rápido que\(\gamma = 30.00\). (a) Ela viaja da Terra para o sistema estelar mais próximo, Alpha Centauri, a 4.300 anos-luz (ly) de distância, conforme medido por um observador ligado à Terra. A que distância estão a Terra e o Alpha Centauri, conforme medido pelo astronauta? (b) Em termos de\(c\), qual é a velocidade dela em relação à Terra? Você pode negligenciar o movimento da Terra em relação ao Sol. (Veja a Figura 3.)

    Na parte a, a distância entre a Terra e o alfa centauri é medida como L-zero. Um relógio dado nesta figura está mostrando um tempo delta-t. Uma nave espacial voando com velocidade de v igual a L-zero sobre o delta-t da Terra até a estrela é mostrada. A parte b mostra o quadro de referência da nave espacial a partir do qual a distância L entre a Terra e a estrela é contraída, pois elas parecem se mover com a mesma velocidade na direção oposta. Na parte b, o relógio mostra menos tempo decorrido do que o relógio na parte a.
    Figura\(\PageIndex{3}\): (a) O observador ligado à Terra mede a distância adequada entre a Terra e o Alfa Centauri. (b) A astronauta observa uma contração de comprimento, já que a Terra e o Alpha Centauri se movem em relação à sua nave. Ela pode percorrer essa distância menor em um tempo menor (seu tempo adequado) sem exceder a velocidade da luz.

    Estratégia

    Primeiro, observe que um ano-luz (ly) é uma unidade de distância conveniente em escala astronômica — é a distância que a luz percorre em um ano. Para a parte (a), observe que a distância de 4.300 ly entre o Alpha Centauri e a Terra é a distância adequada\(l_0\), porque é medida por um observador ligado à Terra a quem ambas as estrelas estão (aproximadamente) estacionárias. Para o astronauta, a Terra e o Alpha Centauri estão se movendo na mesma velocidade e, portanto, a distância entre eles é o comprimento contraído\(L\). Na parte (b), recebemos\(\gamma\), e assim podemos encontrar\(v\) reorganizando a definição de\(\gamma\) expressar\(v\) em termos de\(c\).

    Solução para (a)

    1. Identifique os conhecidos:\(L_0 - 4.300 \, ly; \, \gamma = 30.00\)
    2. Identifique o desconhecido:\(L\)
    3. Escolha a equação apropriada:\(L = \frac{L_0}{\gamma}\)
    4. Reorganize a equação para resolver o desconhecido;\[L = \dfrac{L_0}{\gamma}\]\[= \dfrac{4.300 \, ly}{30.00}\]\[= 0.1433 \, ly\]

    Solução para (b)

    1. Identifique o conhecido:\(\gamma = 30.00\)
    2. Identifique o desconhecido:\(v\) em termos de\(c\)
    3. Escolha a equação apropriada\(\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}\)
    4. Reorganize a equação para resolver o desconhecido:\[\gamma = \dfrac{1}{\sqrt{1 - \frac{v^2}{c^2}}}\]\[ 30.00 = \dfrac{1}{\sqrt{1 - \frac{v^2}{c^2}}}\]

    Ao quadrar os dois lados da equação e reorganizar os termos, obtém-se:\[900.0 = \dfrac{1}{1 - \frac{v^2}{c^2}}\]

    de modo que\[1 - \dfrac{v^2}{c^2} = \dfrac{1}{900.0}\] e\[\dfrac{v^2}{c^2} = 1 - \dfrac{1}{900.0} = 0.99888....\]

    Tomando a raiz quadrada, descobrimos\[\dfrac{v}{c} = 0.99944,\] qual é rearranjada para produzir um valor para a velocidade\[v = 0.9994c.\]

    Discussão

    Primeiro, lembre-se de que você não deve arredondar os cálculos até que o resultado final seja obtido, ou você poderá obter resultados errôneos. Isso é especialmente verdadeiro para cálculos de relatividade especiais, em que as diferenças só podem ser reveladas após várias casas decimais. O efeito relativístico é grande aqui (γ = 30. 00), e vemos que está se aproximando (não igualando) a velocidade da luz. Como a distância medida pela astronauta é muito menor, a astronauta pode percorrê-la em muito menos tempo em seu quadro.

    As pessoas poderiam ser enviadas a distâncias muito grandes (milhares ou até milhões de anos-luz) e envelhecer apenas alguns anos no caminho se viajassem em velocidades extremamente altas. Mas, como emigrantes de séculos passados, eles deixariam a Terra que conhecem para sempre. Mesmo que eles voltassem, milhares a milhões de anos teriam passado na Terra, destruindo a maior parte do que existe agora. Há também um obstáculo prático mais sério para viajar em tais velocidades; energias imensamente maiores do que a física clássica prevê seriam necessárias para atingir velocidades tão altas. Isso será discutido em Relatavistic Energy.

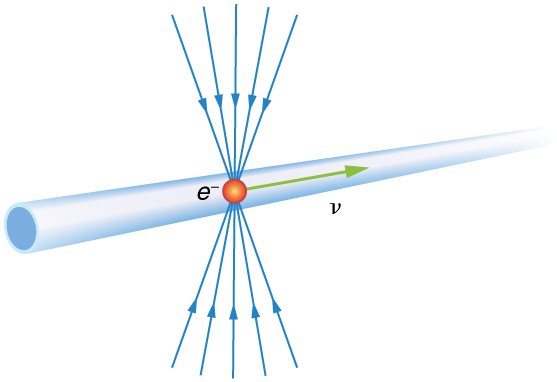
    Por que não notamos a contração do comprimento na vida cotidiana? A distância até o supermercado não parece depender de estarmos nos movendo ou não. Examinando a equação\(L = L_0\sqrt{1 - \frac{v^2}{c^2}}\), vemos que em baixas velocidades\((v <<c)\) os comprimentos são quase iguais, a expectativa clássica. Mas a contração do comprimento é real, se não for comumente experimentada. Por exemplo, uma partícula carregada, como um elétron, viajando em velocidade relativista tem linhas de campo elétrico que são comprimidas ao longo da direção do movimento, conforme vistas por um observador estacionário. (Veja a Figura.) À medida que o elétron passa por um detector, como uma bobina de fio, seu campo interage muito mais brevemente, um efeito observado em aceleradores de partículas, como o Stanford Linear Accelerator (SLAC) de 3 km de extensão. Na verdade, para um elétron viajando pelo tubo do feixe no SLAC, o acelerador e a Terra estão todos se movendo e estão contraídos por comprimento. O efeito relativístico é tão grande que o acelerador tem apenas 0,5 m de comprimento em relação ao elétron. Na verdade, é mais fácil fazer o feixe de elétrons descer pelo tubo, já que o feixe não precisa ser direcionado com tanta precisão para descer por um tubo curto quanto desceria um tubo de 3 km de comprimento. Isso, novamente, é uma verificação experimental da Teoria Especial da Relatividade.

    Um elétron viajando com a velocidade v para a direita através de um tubo horizontal. As linhas do campo elétrico entram nele radialmente.
    Figura\(\PageIndex{41}\): As linhas do campo elétrico de uma partícula carregada de alta velocidade são comprimidas ao longo da direção do movimento pela contração do comprimento. Isso produz um sinal diferente quando a partícula passa por uma bobina, um efeito verificado experimentalmente da contração do comprimento.

    Exercício\(\PageIndex{1}\)

    Uma partícula está viajando pela atmosfera da Terra a uma velocidade de\(0.750c\). Para um observador terrestre, a distância que ele percorre é de 2,50 km. Até onde a partícula viaja no quadro de referência da partícula?

    Responda

    \[L = L_0\sqrt{1 - \dfrac{v^2}{c^2}} = (2.50 \, km)\sqrt{1 - \dfrac{(0.750c)^2}{c^2}} = 1.65 \, km\]

    Resumo

    • Todos os observadores concordam com a velocidade relativa.
    • A distância depende do movimento do observador. O comprimento adequado\(L_0\) é a distância entre dois pontos medida por um observador que está em repouso em relação a ambos os pontos. Os observadores terrestres medem o comprimento adequado ao medir a distância entre dois pontos estacionários em relação à Terra.
    • A contração do comprimento\(L\) é o encurtamento do comprimento medido de um objeto em movimento em relação à moldura do observador:\[L = L_0 \sqrt{1 - \dfrac{v^2}{c^2}} = \dfrac{L_0}{\gamma}.\]

    Glossário

    comprimento adequado
    \(L_0\)a distância entre dois pontos medida por um observador que está em repouso em relação a ambos os pontos; observadores ligados à Terra medem o comprimento adequado ao medir a distância entre dois pontos que estão estacionários em relação à Terra
    contração de comprimento
    \(L\)o encurtamento do comprimento medido de um objeto que se move em relação à estrutura do observador:\(L = L_0\sqrt{1 - \frac{v^2}{c^2}} = \frac{L_0}{\gamma}\)