25.6: Formação de imagem por lentes

Objetivos de

Ao final desta seção, você poderá:

• Liste as regras para rastreamento de raios para lentes finas.
• Ilustre a formação de imagens usando a técnica de rastreamento de raios.
• Determine a potência de uma lente dada a distância focal.

As lentes são encontradas em uma grande variedade de instrumentos ópticos, desde uma simples lupa até o olho até a lente de zoom de uma câmera. Nesta seção, usaremos a lei da refração para explorar as propriedades das lentes e como elas formam imagens.

A palavra lente deriva da palavra latina para grão de lentilha, cujo formato é semelhante ao cristalino convexo da Figura 1. A lente convexa mostrada foi moldada de forma que todos os raios de luz que entram nela paralelamente ao seu eixo se cruzem em um único ponto no lado oposto da lente. (O eixo é definido como uma linha normal à lente em seu centro, conforme mostrado na Figura 1.) Essa lente é chamada de lente convergente (ou convexa) pelo efeito convergente que tem nos raios de luz. Uma visão expandida do caminho de um raio através da lente é mostrada, para ilustrar como o raio muda de direção ao entrar e sair da lente. Como o índice de refração da lente é maior que o do ar, o raio se move em direção à perpendicular à medida que entra e se afasta da perpendicular ao sair. (Isso está de acordo com a lei da refração.) Devido ao formato da lente, a luz é então curvada em direção ao eixo em ambas as superfícies. O ponto no qual os raios se cruzam é definido como o ponto focal F da lente. A distância do centro da lente até seu ponto focal é definida como a distância focal\(f\) da lente. A Figura 2 mostra como uma lente convergente, como a de uma lupa, pode convergir os raios de luz quase paralelos do sol para um pequeno ponto.

Figura\(\PageIndex{1}\): Os raios de luz que entram em uma lente convergente paralelamente ao seu eixo convergem em seu ponto focal F. (o raio 2 está no eixo da lente). A distância do centro da lente até o ponto focal é a distância focal da lente\(f\). Uma visão expandida do caminho percorrido pelo raio 1 mostra as perpendiculares e os ângulos de incidência e refração em ambas as superfícies.

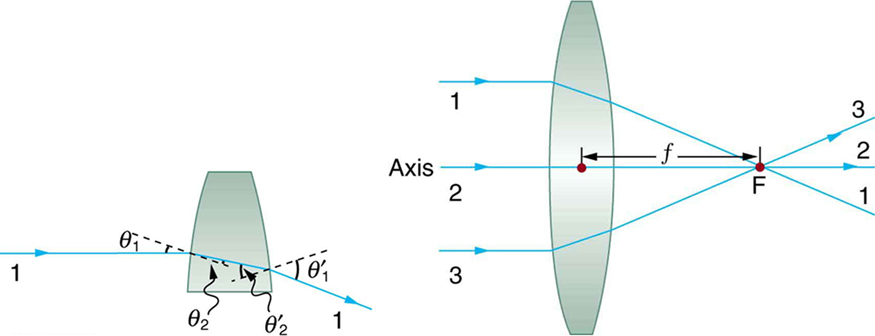
Definição: LENTE CONVERGENTE OU CONVEXA

A lente na qual os raios de luz que entram nela paralelamente ao seu eixo se cruzam em um único ponto do lado oposto com um efeito convergente é chamada de lente convergente.

Definição: PONTO FOCAL F

O ponto em que os raios de luz se cruzam é chamado de ponto focal F da lente.

Definição: DISTÂNCIA FOCAL\(f\)

A distância do centro da lente até seu ponto focal é chamada de distância focal\(f\).

Figura\(\PageIndex{2}\): A luz solar focada por uma lupa convergente pode queimar papel. Os raios de luz do sol são quase paralelos e se cruzam no ponto focal da lente. Quanto mais poderosa a lente, mais perto da lente os raios se cruzarão.

Quanto maior o efeito de uma lente sobre os raios de luz, mais poderosa ela é considerada. Por exemplo, uma lente convergente poderosa focalizará os raios de luz paralelos mais perto de si mesma e terá uma distância focal menor do que uma lente fraca. A luz também se concentrará em um local menor e mais intenso para obter uma lente mais potente. A potência\(P\) de uma lente é definida como sendo o inverso de sua distância focal:

Definição: POTÊNCIA\(P\)

A potência\(P\) de uma lente é definida como sendo o inverso de sua distância focal. Em forma de equação, isso é

\[P = \frac{1}{f}.\]

onde\(f\) está a distância focal da lente, que deve ser dada em metros (e não em cm ou mm). A potência de uma lente\(P\) tem as dioptrias unitárias (D), desde que a distância focal seja dada em metros. Isso é\(1 D = 1/m\) ou\(1 m^{-1}\). (Observe que essa potência (potência óptica, na verdade) não é a mesma que a potência em watts definida em “Trabalho, energia e recursos energéticos”. É um conceito relacionado ao efeito de dispositivos ópticos na luz.) Os optometristas prescrevem óculos comuns e lentes de contato em unidades de dioptrias.

Exemplo\(\PageIndex{1}\): What is the Power of a Common Magnifying Glass?

Suponha que você tire uma lupa em um dia ensolarado e descubra que ela concentra a luz do sol em um pequeno ponto a 8,00 cm da lente. Quais são a distância focal e a potência da lente?

Estratégia:

A situação aqui é a mesma mostrada na Figura 1 e na Figura 2. O Sol está tão distante que os raios do Sol são quase paralelos quando chegam à Terra. A lupa é uma lente convexa (ou convergente), focando os raios de luz solar quase paralelos. Assim, a distância focal da lente é a distância da lente até o ponto, e sua potência é o inverso dessa distância (em m).

Solução

A distância focal da lente é a distância do centro da lente até o ponto, dada como 8,00 cm. Assim,\[f = 8.00 cm.\] para encontrar a potência da lente, devemos primeiro converter a distância focal em metros; em seguida, substituímos esse valor na equação por potência. Isso dá\[P = \frac{1}{f} = \frac{1}{0.0800 m} = 12.5 D.\]

Discussão:

Essa é uma lente relativamente poderosa. A potência de uma lente em dioptrias não deve ser confundida com o conceito familiar de potência em watts. É lamentável que a palavra “poder” seja usada para dois conceitos completamente diferentes. Se você examinar uma receita de óculos, notará os poderes das lentes dados em dioptrias. Se você examinar a etiqueta de um motor, notará a taxa de consumo de energia dada como uma potência em watts.

A figura\(\PageIndex{3}\) mostra uma lente côncava e o efeito que ela tem sobre os raios de luz que entram nela paralelamente ao seu eixo (o caminho percorrido pelo raio 2 na figura é o eixo da lente). A lente côncava é uma lente divergente, pois faz com que os raios de luz se afastem (diverjam) de seu eixo. Nesse caso, a lente foi moldada de forma que todos os raios de luz que entram nela paralelamente ao seu eixo pareçam se originar do mesmo ponto\(F\),, definido como o ponto focal de uma lente divergente. A distância do centro da lente até o ponto focal é novamente chamada de distância focal\(f\) da lente. Observe que a distância focal e a potência de uma lente divergente são definidas como negativas. Por exemplo, se a distância até a\(F\) Figura 3 for de 5,00 cm, a distância focal é\(f = -5.00 cm\) e a potência da lente é\(P = -20D\). Uma visão expandida do caminho de um raio através da lente é mostrada na figura para ilustrar como a forma da lente, junto com a lei da refração, faz com que o raio siga seu caminho específico e seja divergido.

Figura\(\PageIndex{3}\): Os raios de luz que entram em uma lente divergente paralelamente ao seu eixo são divergentes e todos parecem se originar em seu ponto focal\(F\). As linhas tracejadas não são raios — elas indicam as direções de onde os raios parecem vir. A distância focal\(f\) de uma lente divergente é negativa. Uma visão expandida do caminho percorrido pelo raio 1 mostra as perpendiculares e os ângulos de incidência e refração em ambas as superfícies.

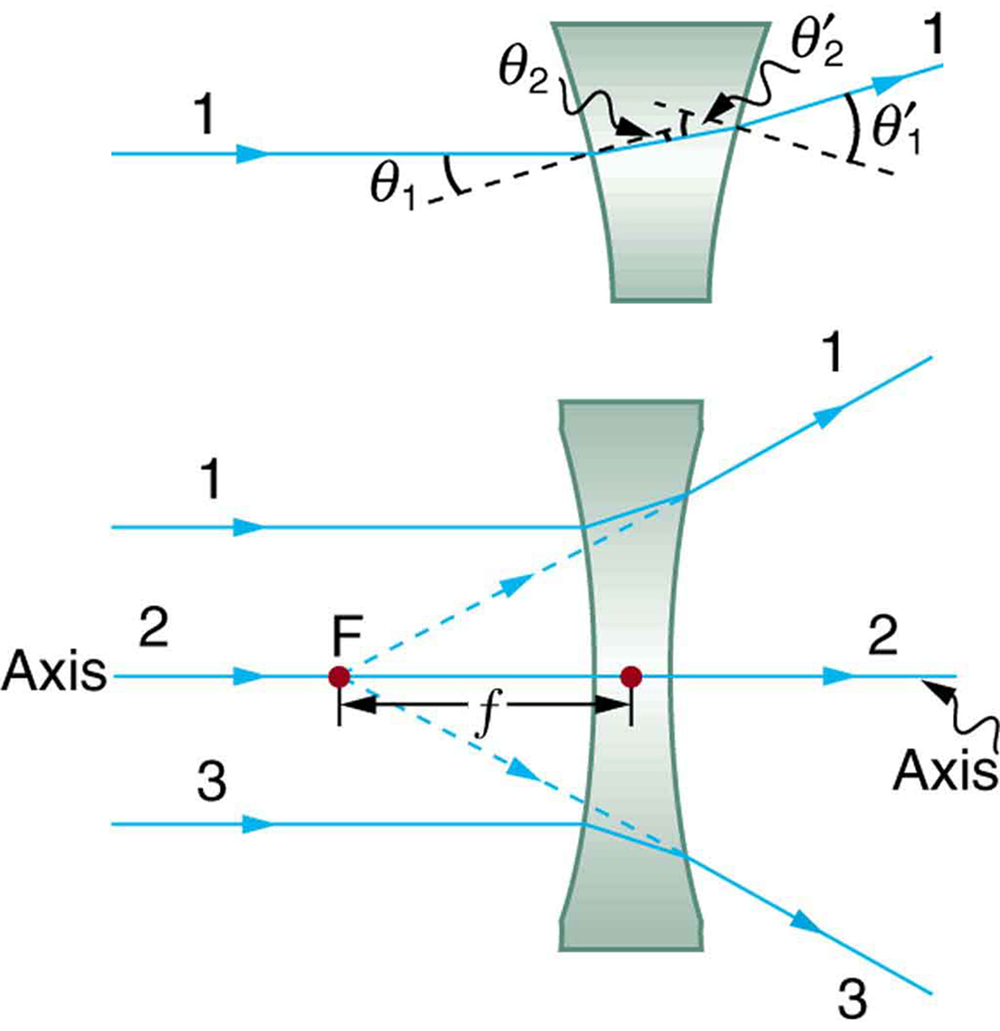
Definição: LENTE DIVERGENTE

Uma lente que faz com que os raios de luz se afastem de seu eixo é chamada de lente divergente.

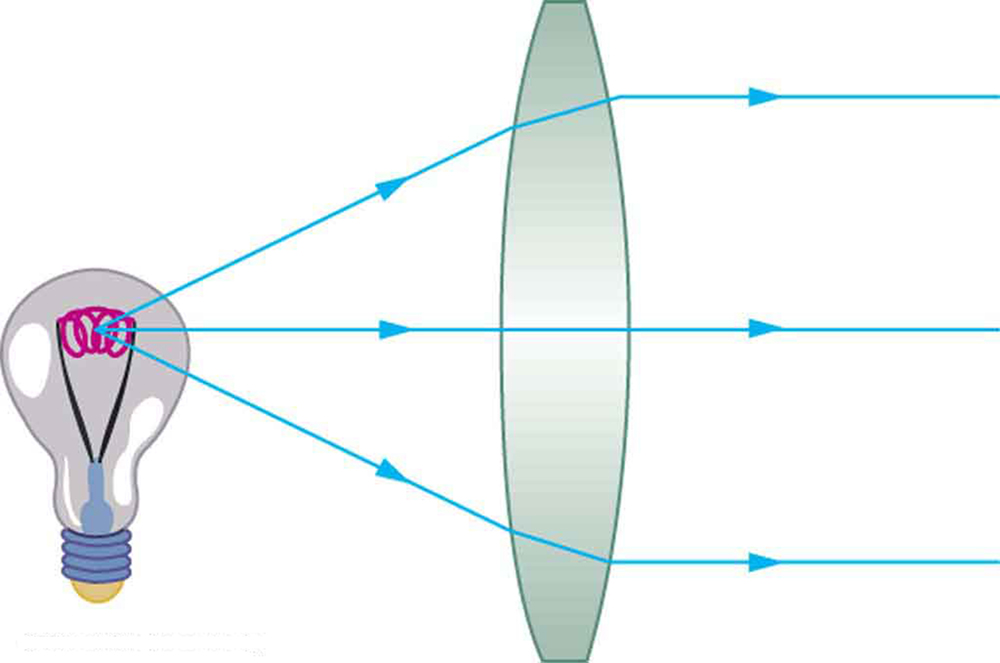
Conforme observado na discussão inicial sobre a lei da refração em “A Lei da Refração”, os caminhos dos raios de luz são exatamente reversíveis. Isso significa que a direção das setas pode ser invertida para todos os raios em Figuras\(\PageIndex{1}\) e Figuras\(\PageIndex{3}\). Por exemplo, se uma fonte de luz pontual for colocada no ponto focal de uma lente convexa, conforme mostrado na Figura 4, raios de luz paralelos emergem do outro lado.

Figura 1. Essa técnica é usada em faróis e às vezes em semáforos para produzir um feixe de luz direcional de uma fonte que emite luz em todas as direções.

Ray Tracing e lentes finas

O traçado de raios é a técnica de determinar ou seguir (traçar) os caminhos percorridos pelos raios de luz. Para os raios que passam pela matéria, a lei da refração é usada para traçar os caminhos. Aqui, usamos o traçado de raios para nos ajudar a entender a ação das lentes em situações que vão desde a formação de imagens em filme até a ampliação de letras pequenas e a correção da miopia. Embora o traçado de raios para lentes complicadas, como as encontradas em câmeras sofisticadas, possa exigir técnicas de computador, há um conjunto de regras simples para rastrear raios por meio de lentes finas. Uma lente fina é definida como aquela cuja espessura permite a refração dos raios, conforme ilustrado na Figura\(\PageIndex{1}\), mas não permite propriedades como dispersão e aberrações. Uma lente fina ideal tem duas superfícies refratárias, mas a lente é fina o suficiente para supor que os raios de luz se curvam apenas uma vez. Uma lente simétrica fina tem dois pontos focais, um em cada lado e ambos à mesma distância da lente (Figura\(\PageIndex{5}\)). Outra característica importante de uma lente fina é que os raios de luz através de seu centro são desviados em uma quantidade insignificante, conforme visto na Figura\(\PageIndex{6}\).

Definição: LENTE FINA

Uma lente fina é definida como aquela cuja espessura permite a refração dos raios, mas não permite propriedades como dispersão e aberrações.

EXPERIMENTO PARA LEVAR PARA CASA: UMA VISITA AO OFTALMOLOGISTA

Olhe seus óculos (ou os de um amigo) para trás e para frente e comente se eles agem como lentes finas.

Figura\(\PageIndex{5}\): As lentes finas têm a mesma distância focal em ambos os lados. (a) Raios de luz paralelos que entram em uma lente convergente pela direita se cruzam em seu ponto focal à esquerda. (b) Os raios de luz paralelos que entram em uma lente divergente pela direita parecem vir do ponto focal à direita.

Figura\(\PageIndex{6}\): O raio de luz que passa pelo centro de uma lente fina é desviado em uma quantidade insignificante e presume-se que emerja paralelamente ao seu caminho original (mostrado como uma linha sombreada).

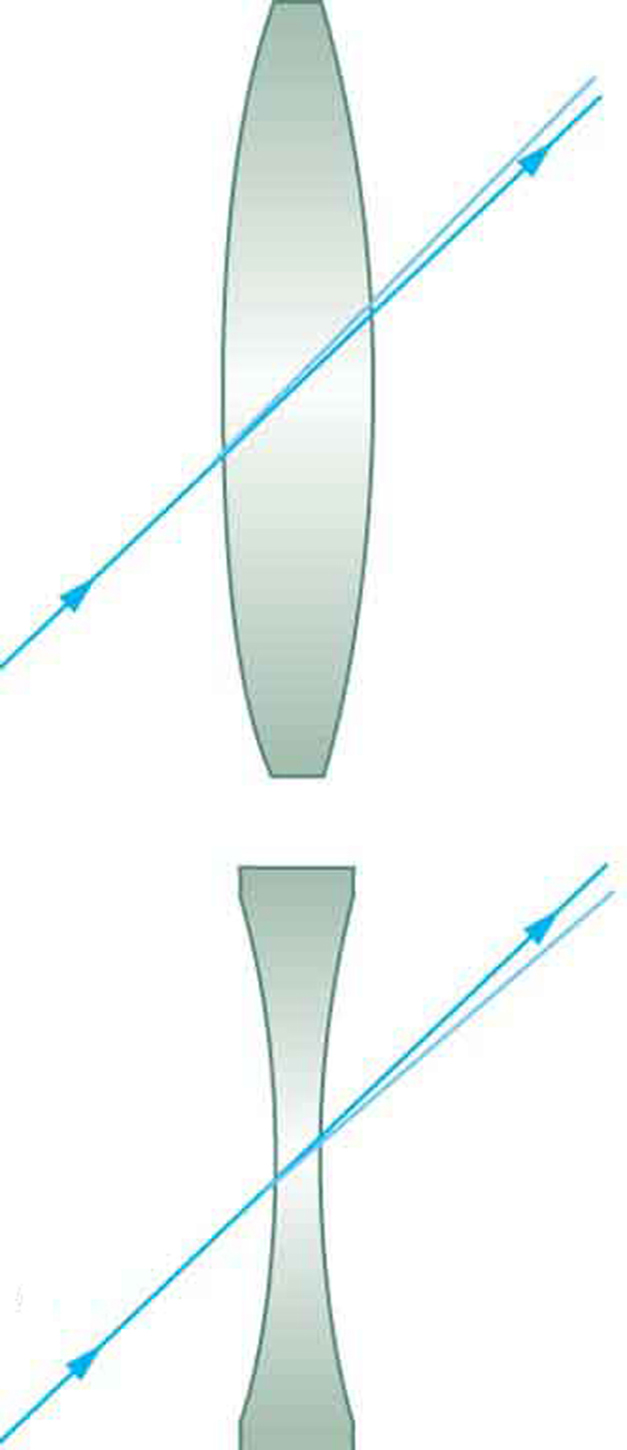
Usando papel, lápis e uma borda reta, o traçado de raios pode descrever com precisão a operação de uma lente. As regras do Ray Tracing para lentes finas são baseadas nas ilustrações já discutidas:

REGRAS PARA RASTREAMENTO DE RAIOS (para lentes finas)

1. Um raio que entra em uma lente convergente paralelamente ao seu eixo passa pelo ponto focal F da lente do outro lado. (Veja os raios 1 e 3 na Figura\(\PageIndex{1}\)).
2. Um raio entrando em uma lente divergente paralela ao seu eixo parece vir do ponto focal F. (Veja os raios 1 e 3 na Figura\(\PageIndex{3}\)).
3. Um raio passando pelo centro de uma lente convergente ou divergente não muda de direção. (Veja a Figura\(\PageIndex{6}\) e veja o raio 2 na Figura\(\PageIndex{1}\) e\(\PageIndex{3}\)).
4. Um raio que entra em uma lente convergente através de seu ponto focal sai paralelamente ao seu eixo. (O inverso dos raios 1 e 3 na Figura\(\PageIndex{1}\)).
5. Um raio que entra em uma lente divergente indo em direção ao ponto focal no lado oposto sai paralelamente ao eixo. (O inverso dos raios 1 e 3 na Figura\(\PageIndex{3}\)).

Formação de imagem por lentes finas

Em algumas circunstâncias, uma lente forma uma imagem óbvia, como quando um projetor de filme projeta uma imagem em uma tela. Em outros casos, a imagem é menos óbvia. Onde, por exemplo, está a imagem formada pelos óculos? Usaremos o traçado de raios para lentes finas para ilustrar como elas formam imagens e desenvolveremos equações para descrever quantitativamente a formação da imagem.

Considere um objeto a alguma distância de uma lente convergente, conforme mostrado na Figura\(\PageIndex{7}\). Para encontrar a localização e o tamanho da imagem formada, traçamos os caminhos dos raios de luz selecionados originados de um ponto do objeto, neste caso, o topo da cabeça da pessoa. A figura mostra três raios da parte superior do objeto que podem ser rastreados usando as regras de traçado de raios fornecidas acima. (Os raios partem desse ponto indo em várias direções, mas nos concentramos em apenas algumas com caminhos fáceis de traçar.) O primeiro raio é aquele que entra na lente paralelamente ao seu eixo e passa pelo ponto focal do outro lado (regra 1). O segundo raio passa pelo centro da lente sem mudar de direção (regra 3). O terceiro raio passa pelo ponto focal mais próximo ao entrar na lente e deixa a lente paralela ao seu eixo (regra 4). Os três raios se cruzam no mesmo ponto do outro lado da lente. A imagem do topo da cabeça da pessoa está localizada nesse ponto. Todos os raios que vêm do mesmo ponto na parte superior da cabeça da pessoa são refratados de forma a se cruzarem no ponto mostrado. Raios de outro ponto do objeto, como a fivela do cinto, também se cruzarão em outro ponto comum, formando uma imagem completa, conforme mostrado. Embora três raios sejam traçados na Figura\(\PageIndex{7}\), apenas dois são necessários para localizar a imagem. É melhor traçar raios para os quais existem regras simples de rastreamento de raios. Antes de aplicar o traçado de raios em outras situações, vamos considerar o exemplo mostrado na Figura 7 com mais detalhes.

Figura\(\PageIndex{7}\): O traçado de raios é usado para localizar a imagem formada por uma lente. Raios originados do mesmo ponto do objeto são traçados — cada um dos três raios escolhidos segue uma das regras de traçado de raios, para que seus caminhos sejam fáceis de determinar. A imagem está localizada no ponto em que os raios se cruzam. Nesse caso, uma imagem real — que pode ser projetada em uma tela — é formada.

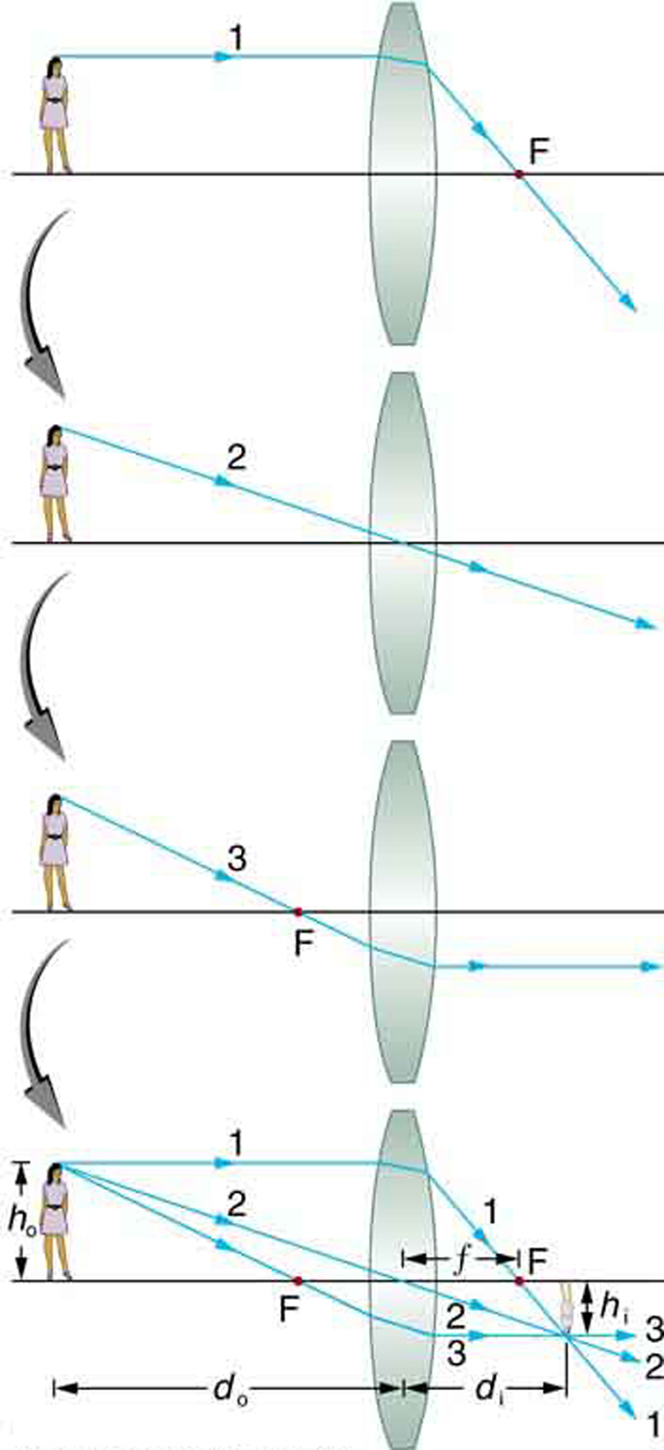
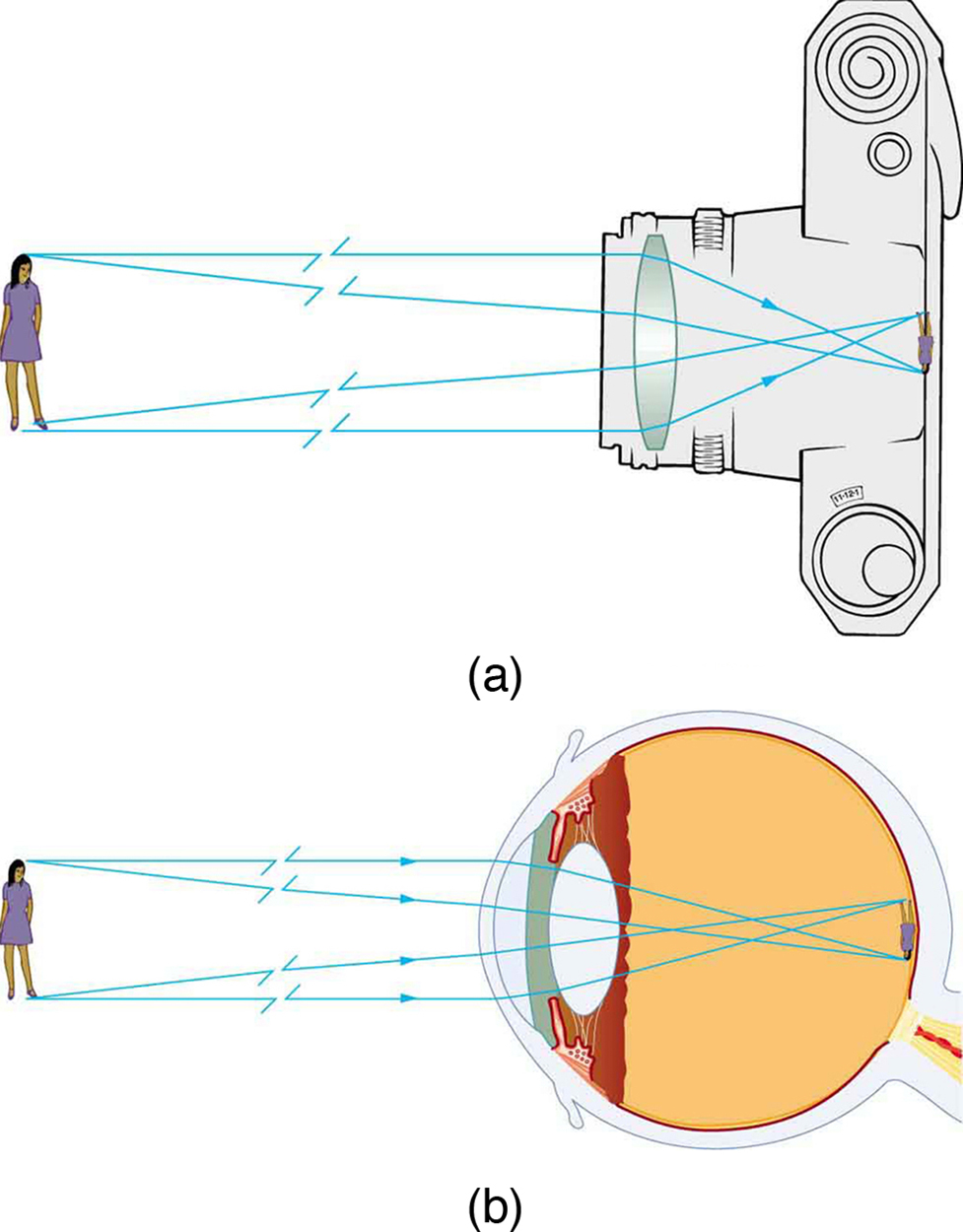
A imagem formada na Figura\(\PageIndex{7}\) é uma imagem real, o que significa que ela pode ser projetada. Ou seja, os raios de luz de um ponto do objeto na verdade se cruzam no local da imagem e podem ser projetados em uma tela, em um pedaço de filme ou na retina de um olho, por exemplo. A figura\(\PageIndex{8}\) mostra como essa imagem seria projetada no filme pela lente de uma câmera. Essa figura também mostra como uma imagem real é projetada na retina pela lente de um olho. Observe que a imagem está lá, seja projetada em uma tela ou não.

Definição: IMAGEM REAL

A imagem na qual os raios de luz de um ponto do objeto realmente se cruzam no local da imagem e podem ser projetados em uma tela, em um pedaço de filme ou na retina de um olho é chamada de imagem real.

Figura\(\PageIndex{8}\): Imagens reais podem ser projetadas. (a) Uma imagem real da pessoa é projetada no filme. (b) A natureza convergente das múltiplas superfícies que compõem o olho resulta na projeção de uma imagem real na retina.

Várias distâncias importantes aparecem na Figura 7. Definimos\(d_{0}\) como sendo o objeto de distância, a distância de um objeto do centro de uma lente. A distância da imagem\(d_{i}\) é definida como a distância da imagem do centro de uma lente. A altura do objeto e a altura da imagem recebem os símbolos\(h_{0}\) e\(h_{i}\), respectivamente. As imagens que aparecem na vertical em relação ao objeto têm alturas positivas e as invertidas têm alturas negativas. Usando as regras do traçado de raios e fazendo um desenho em escala com papel e lápis, como na Figura 7, podemos descrever com precisão a localização e o tamanho de uma imagem. Mas o benefício real do traçado de raios está em visualizar como as imagens são formadas em uma variedade de situações. Para obter informações numéricas, usamos um par de equações que podem ser derivadas de uma análise geométrica do traçado de raios para lentes finas. As equações da lente fina são

\[\frac{1}{d_{0}} + \frac{1}{d_{i}} = \frac{1}{f}\label{25.7.1}\]

e

\[\frac{h_{i}}{h_{0}} = - \frac{d_{i}}{d_{0}} = m.\label{25.7.2}\]

Definimos a proporção entre a altura da imagem e a altura do objeto (\(h_{i}/h_{0}\)) para ser a ampliação\(m\). (O sinal de menos na equação acima será discutido em breve.) As equações de lentes finas são amplamente aplicáveis a todas as situações que envolvem lentes finas (e espelhos “finos”, como veremos mais adiante). Exploraremos muitas características da formação de imagens nos seguintes exemplos trabalhados.

Definição: DISTÂNCIA DA IMAGEM

A distância da imagem do centro da lente é chamada de distância da imagem.

Definição: EQUAÇÕES E AMPLIAÇÃO DE LENTES FINAS

\[\frac{1}{d_{0}} + \frac{1}{d_{i}} = \frac{1}{f}\label{25.7.1}\]

\[\frac{h_{i}}{h_{0}} = - \frac{d_{i}}{d_{0}} = m \label{25.7.2}\]

Exemplo\(\PageIndex{2}\): Finding the Image of a Light Bulb Filament by Ray Tracing and by the Thin Lens Equations

Uma lâmpada de vidro transparente é colocada a 0,750 m de uma lente convexa com uma distância focal de 0,500 m, conforme mostrado na figura. Use o traçado de raios para obter uma localização aproximada da imagem. Em seguida, use as equações de lentes finas para calcular

1. a localização da imagem e
2. sua ampliação.

Verifique se o traçado de raios e as equações de lentes finas produzem resultados consistentes.

Figura\(\PageIndex{9}\): Uma lâmpada colocada a 0,750 m de uma lente com uma distância focal de 0,500 m produz uma imagem real em um cartaz, conforme discutido no exemplo acima. O traçado de raios prevê a localização e o tamanho da imagem.

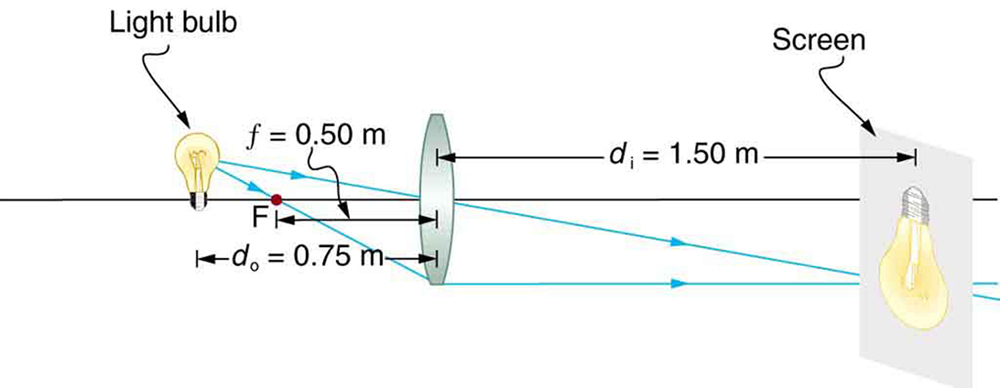
Estratégia e conceito

Como o objeto é colocado mais longe de uma lente convergente do que a distância focal da lente, essa situação é análoga às ilustradas na Figura 7 e na Figura 8. O traçado de raios em escala deve produzir resultados semelhantes para\(d_{i}\). Soluções numéricas para\(d_{i}\) e\(m\) podem ser obtidas usando as equações de lente fina, observando que\(d_{o} = 0.750 m\)\(f = 0.500 m\) e.

Soluções (Ray Tracing)

O traçado de raios em escala na Figura 9 mostra dois raios de um ponto no filamento da lâmpada cruzando cerca de 1,50 m no outro lado da lente. Assim, a distância da imagem\(d_{i}\) é de cerca de 1,50 m. Da mesma forma, a altura da imagem com base no traçado de raios é maior do que a altura do objeto em cerca de um fator de 2, e a imagem é invertida. Isso\(m\) é cerca de —2. O sinal de menos indica que a imagem está invertida.

As equações de lentes finas podem ser usadas para encontrar a\(d_{i}\) partir das informações fornecidas:\[\frac{1}{d_{o}} + \frac{1}{d_{i}} = \frac{1}{f} . \] Reorganizar para isolar\(d_{i}\) dá\[\frac{1}{d_{i}} = \frac{1}{f} - \frac{1}{d_{o}}.\] Inserir quantidades conhecidas fornece um valor para\(1/d_{i}\):\[\frac{1}{d_{i}} = \frac{1}{0.500 m} - \frac{1}{0.750m} = \frac{0.667}{m}.\] Isso deve ser invertido para encontrar\(d_{i}\):\[d_{i} = \frac{m}{0.667} = 1.50m .\] Observe que outra maneira de encontrar\(d_{i}\) é reorganizar a equação:\[\frac{1}{d_{i}} = \frac{1}{f} - \frac{1}{d_{o}}.\] Isso produz a equação para a distância da imagem como:\[d_{i} = \frac{fd_{o}}{d_{o} - f}.\label{25.7.3}\] Observe que não há inversão aqui.

As equações de lentes finas podem ser usadas para encontrar a ampliação\(m\), já que ambas\(d_{i}\)\(d_{o}\) são conhecidas. Inserir seus valores dá

\[m = -\frac{d_{i}}{d_{o}} = -\frac{1.50 m}{0.750 m} = -2.00. \label{25.7.4}\]

Discussão

Observe que o sinal de menos faz com que a ampliação seja negativa quando a imagem é invertida. O traçado de raios e o uso de equações de lente fina produzem resultados consistentes. As equações de lentes finas fornecem os resultados mais precisos, sendo limitadas apenas pela precisão das informações fornecidas. O traçado de raios é limitado pela precisão com a qual você pode desenhar, mas é altamente útil tanto conceitual quanto visualmente.

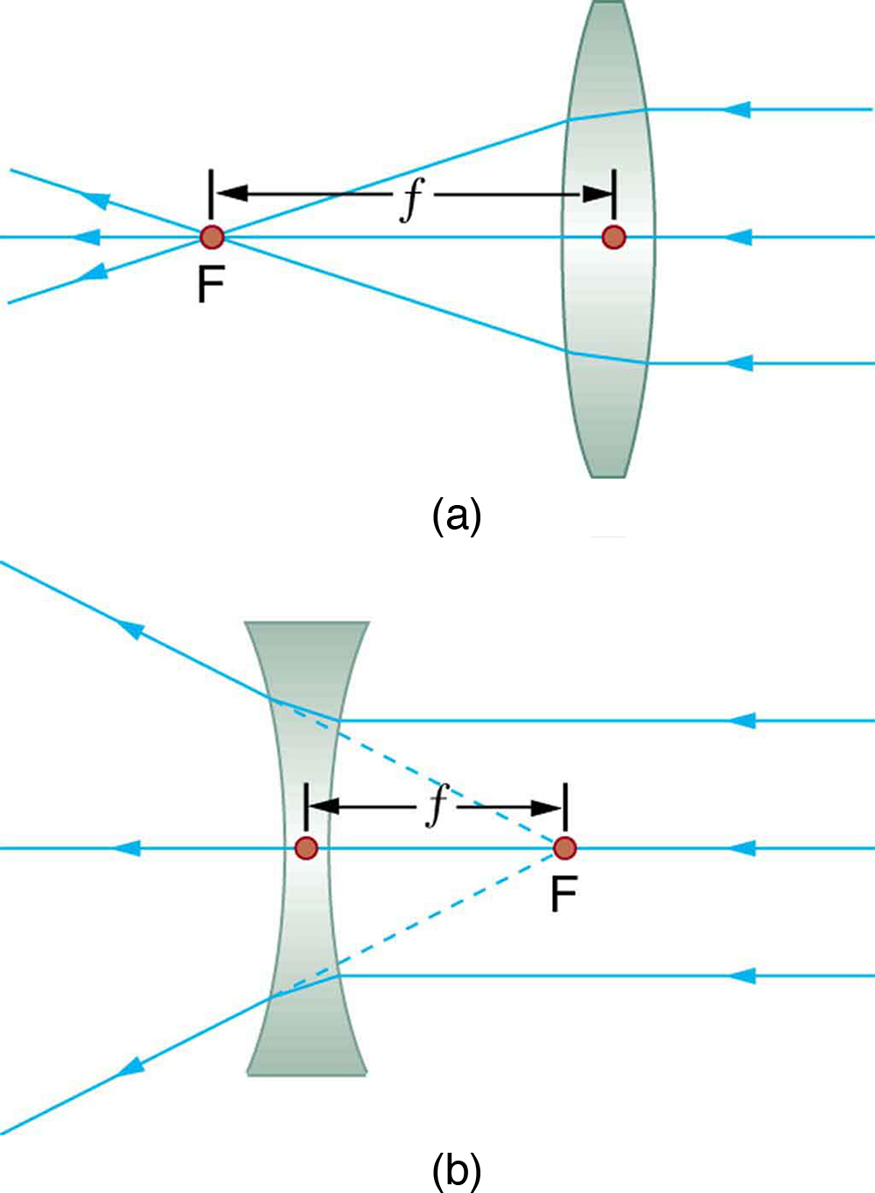
Imagens reais, como a considerada no exemplo anterior, são formadas por lentes convergentes sempre que um objeto está mais distante da lente do que sua distância focal. Isso vale para projetores de filmes, câmeras e olhos. Vamos nos referir a elas como imagens do caso 1. Uma imagem do caso 1 é formada quando\(d_{o} \gt f\) e\(f\) é positiva, como na Figura\(\PageIndex{10a}\). (Um resumo dos três casos ou tipos de formação de imagem aparece no final desta seção.)

Um tipo diferente de imagem é formado quando um objeto, como o rosto de uma pessoa, é mantido próximo a uma lente convexa. A imagem é vertical e maior do que o objeto, como visto na Figura\(\PageIndex{10b}\), e por isso a lente é chamada de lupa. Se você puxar lentamente a lupa para longe da face, verá que a ampliação aumenta constantemente até que a imagem comece a ficar desfocada. Afastar ainda mais a lupa produz uma imagem invertida, conforme mostrado na Figura\(\PageIndex{10a}\). A distância na qual a imagem fica desfocada e além da qual ela se inverte é a distância focal da lente. Para usar uma lente convexa como lupa, o objeto deve estar mais próximo da lente convergente do que sua distância focal. Isso é chamado de imagem do caso 2. Uma imagem do caso 2 é formada quando\(d_{o} \lt f\) e\(f\) é positiva.

Figura\(\PageIndex{10}\): (a) Quando uma lente convergente é mantida mais longe da face do que a distância focal da lente, uma imagem invertida é formada. Esta é uma imagem do caso 1. Observe que a imagem está em foco, mas o rosto não, porque a imagem está muito mais próxima da câmera tirando essa fotografia do que do rosto. (crédito: DaMongMan, Flickr) (b) Uma imagem ampliada de um rosto é produzida colocando-a mais próxima da lente convergente do que sua distância focal. Esta é uma imagem do caso 2. (crédito: Casey Fleser, Flickr)

A figura\(\PageIndex{11}\) usa o traçado de raios para mostrar como uma imagem é formada quando um objeto é mantido mais próximo de uma lente convergente do que sua distância focal. Os raios vindos de um ponto comum no objeto continuam divergindo depois de passar pela lente, mas todos parecem ter origem em um ponto no local da imagem. A imagem está no mesmo lado da lente que o objeto e está mais distante da lente do que o objeto. Essa imagem, como todas as imagens do caso 2, não pode ser projetada e, portanto, é chamada de imagem virtual. Os raios de luz parecem se originar apenas em uma imagem virtual; na verdade, eles não passam por esse local no espaço. Uma tela colocada no local de uma imagem virtual receberá somente luz difusa do objeto, não raios focalizados da lente. Além disso, uma tela colocada no lado oposto da lente receberá raios que ainda estão divergindo e, portanto, nenhuma imagem será projetada nela. Podemos ver a imagem ampliada com nossos olhos, porque a lente do olho converge os raios em uma imagem real projetada em nossa retina. Finalmente, notamos que uma imagem virtual é vertical e maior que o objeto, o que significa que a ampliação é positiva e maior que 1.

Figura\(\PageIndex{11}\): O traçado de raios prevê a localização e o tamanho da imagem de um objeto mantido mais próximo de uma lente convergente do que sua distância focal. O raio 1 entra paralelamente ao eixo e sai pelo ponto focal no lado oposto, enquanto o raio 2 passa pelo centro da lente sem mudar de caminho. Os dois raios continuam divergindo do outro lado da lente, mas ambos parecem vir de um ponto comum, localizando a imagem vertical, ampliada e virtual. Esta é uma imagem do caso 2.

Definição: IMAGEM VIRTUAL

Uma imagem que está do mesmo lado da lente que o objeto e não pode ser projetada em uma tela é chamada de imagem virtual.

Exemplo\(\PageIndex{3}\): Image Produced by a Magnifying Glass

Suponha que o livro na Figura\(\PageIndex{11a}\) esteja a 7,50 cm de uma lente convexa de distância focal de 10,0 cm, como uma lupa típica poderia ter. Qual ampliação é produzida?

Estratégia e conceito

Recebemos isso\(d_{o} = 7.50 cm\) e\(f = 10.0cm\), portanto, temos uma situação em que o objeto é colocado mais próximo da lente do que sua distância focal. Portanto, esperamos obter uma imagem virtual de caso 2 com uma ampliação positiva maior que 1. O traçado de raios produz uma imagem como a mostrada na Figura 11, mas usaremos as equações de lente fina para obter soluções numéricas neste exemplo.

Solução

Para encontrar a ampliação\(m\), tentamos usar a equação de ampliação,\(m = -d_{i}/d_{o}\). Não temos um valor para\(d_{i}\), então devemos primeiro encontrar a localização da imagem usando a equação da lente. (O procedimento é o mesmo seguido no exemplo anterior, onde\(d_{o}\) e\(f\) eram conhecidos.) Reorganizando a equação de ampliação para isolar\(d_{i}\) fornece\[\frac{1}{d_{i}} = \frac{1}{f} - \frac{1}{d_{o}}.\] Inserindo valores conhecidos, obtemos um valor para\(1/d_{i}\):\[\frac{1}{d_{i}} = \frac{1}{10.0 cm} - \frac{1}{7.50 cm} = \frac{-0.0333}{cm}.\] Isso deve ser invertido para encontrar\(d_{i}\):\[d_{i} = - \frac{cm}{0.0333} = -30.0 cm.\] Agora, a equação da lente fina pode ser usada para encontrar a ampliação\(m\), uma vez que tanto\(d_{i}\) e \(d_{o}\)são conhecidos. Inserir seus valores dá\[m = -\frac{d_{i}}{d_{o}} = - \frac{-30.0 cm}{7.50 cm} = 4.00.\]

Discussão

Vários resultados neste exemplo são verdadeiros para todas as imagens do caso 2, além de serem consistentes com a Figura 11. A ampliação é realmente positiva (conforme previsto), o que significa que a imagem está na vertical. A ampliação também é maior que 1, o que significa que a imagem é maior do que o objeto — nesse caso, por um fator de 4. Observe que a distância da imagem é negativa. Isso significa que a imagem está do mesmo lado da lente que o objeto. Assim, a imagem não pode ser projetada e é virtual. (Valores negativos de\(d_{i}\) ocorrem para imagens virtuais.) A imagem está mais distante da lente do que o objeto, já que a distância da imagem é maior em magnitude do que a distância do objeto. A localização da imagem não é óbvia quando você olha através de uma lupa. Na verdade, como a imagem é maior do que o objeto, você pode pensar que a imagem está mais próxima do que o objeto. Mas a imagem está mais distante, fato que é útil para corrigir a hipermetropia, como veremos em uma seção posterior.

Um terceiro tipo de imagem é formado por uma lente divergente ou côncava. Experimente examinar os óculos destinados a corrigir a miopia. (Figura\(\PageIndex{12}\)). Você verá uma imagem vertical, mas menor que o objeto. Isso significa que a ampliação é positiva, mas menor que 1. O diagrama de raios na Figura 13 mostra que a imagem está do mesmo lado da lente que o objeto e, portanto, não pode ser projetada — é uma imagem virtual. Observe que a imagem está mais próxima da lente do que do objeto. Esta é uma imagem do caso 3, formada para qualquer objeto por uma distância focal negativa ou lente divergente.

Figura\(\PageIndex{12}\): Um carro visto através de uma lente côncava ou divergente parece na vertical. Esta é uma imagem do caso 3. (crédito: Daniel Oines, Flickr)

Figura\(\PageIndex{13}\): O traçado de raios prevê a localização e o tamanho da imagem para uma lente côncava ou divergente. O raio 1 entra paralelamente ao eixo e é dobrado de forma que pareça se originar do ponto focal. O raio 2 passa pelo centro da lente sem mudar de caminho. Os dois raios parecem vir de um ponto comum, localizando a imagem vertical. Esta é uma imagem do caso 3, que está mais próxima da lente do que o objeto e menor em altura.

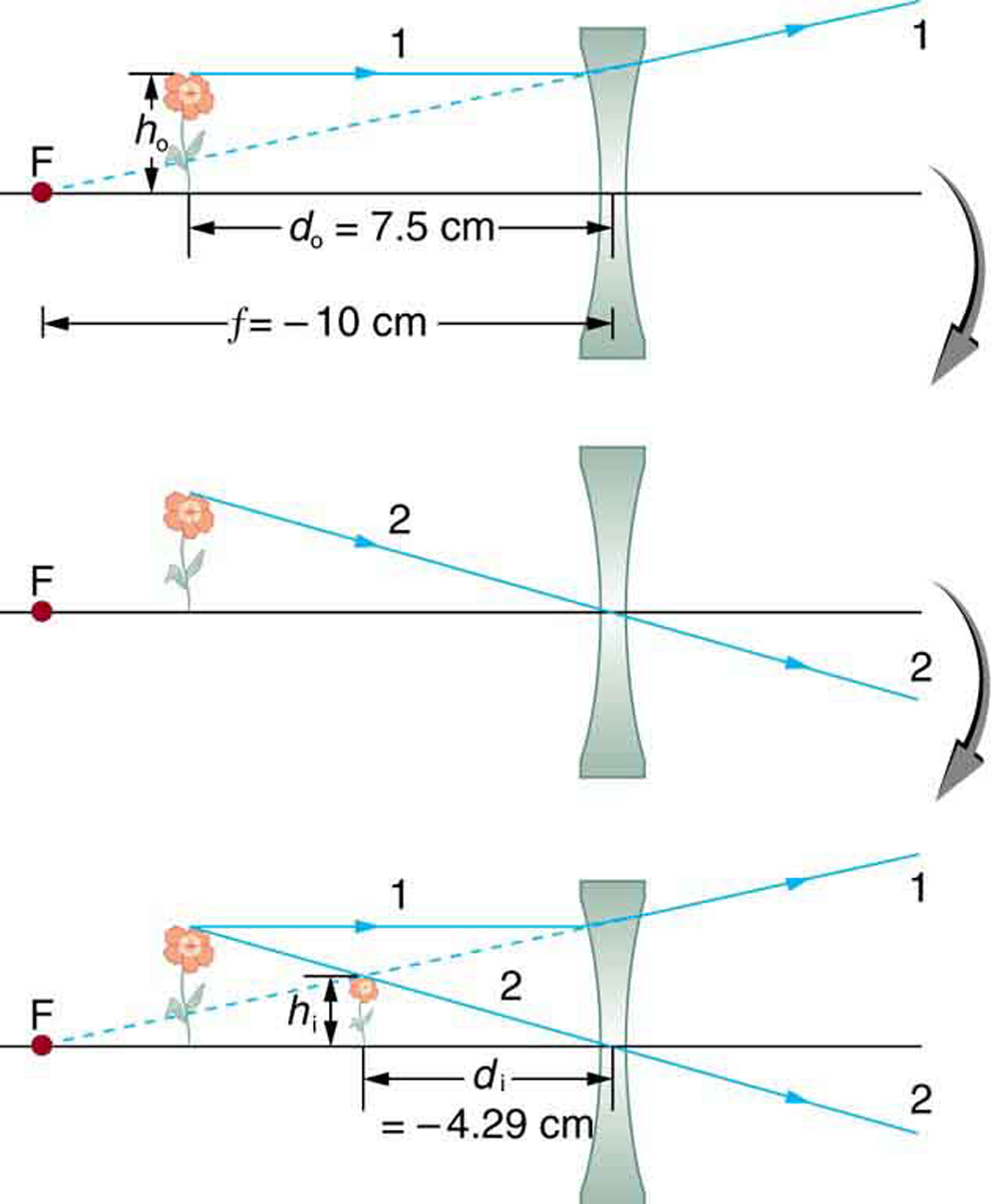
Exemplo\(\PageIndex{4}\): Image Produced by a Concave Lens

Suponha que um objeto, como uma página de livro, seja mantido a 7,50 cm de uma lente côncava de distância focal de —10,0 cm. Essa lente pode ser usada em óculos para corrigir a miopia pronunciada. Qual ampliação é produzida?

Estratégia e conceito

Este exemplo é idêntico ao anterior, exceto que a distância focal é negativa para uma lente côncava ou divergente. O método de solução é, portanto, o mesmo, mas os resultados são diferentes em aspectos importantes.

Solução

Para encontrar a ampliação\(m\), devemos primeiro encontrar a distância da imagem\(d_{i}\) usando a equação de lente fina

\[\frac{1}{d_{i}} = \frac{1}{f} - \frac{1}{d_{o}},\]

ou seu rearranjo alternativo

\[d_{i} = \frac{fd_{o}}{d_{o} - f}.\]

Recebemos isso\(f = -10.00 cm\)\(d_{o} = 7.50 cm\) e. Inserir essas informações gera um valor para\(1/d_{i}\):

\[\frac{1}{d_{i}} = \frac{1}{-10.0 cm} - \frac{1}{7.50 cm} = \frac{-0.2333}{cm}.\]

Isso deve ser invertido para encontrar\(d_{i}\):

\[d_{i} = -\frac{cm}{0.2333} = -4.29 cm.\]

Ou\[d_{i} = \frac{\left(7.5\right) \left(-10\right)}{\left(7.5 - \left(-10\right)\right)} = -75/17.5 = -4.29cm.\] agora, a equação de ampliação pode ser usada para encontrar a ampliação\(m\), já que ambas\(d_{i}\)\(d_{o}\) são conhecidas. Inserir seus valores dá

\[m = - \frac{d_{i}}{d_{o}} = - \frac{-4.29 cm}{7.50 cm} = 0.571.\]

Discussão:

Vários resultados neste exemplo são verdadeiros para todas as imagens do caso 3, além de serem consistentes com a Figura 13. A ampliação é positiva (conforme previsto), o que significa que a imagem está na vertical. A ampliação também é menor que 1, o que significa que a imagem é menor que o objeto — nesse caso, um pouco mais da metade de seu tamanho. A distância da imagem é negativa, o que significa que a imagem está do mesmo lado da lente que o objeto. (A imagem é virtual.) A imagem está mais próxima da lente do que o objeto, já que a distância da imagem é menor em magnitude do que a distância do objeto. A localização da imagem não é óbvia quando você olha através de uma lente côncava. Na verdade, como a imagem é menor que o objeto, você pode pensar que ela está mais distante. Mas a imagem está mais próxima do que o objeto, fato que é útil para corrigir a miopia, como veremos em uma seção posterior.

A tabela resume os três tipos de imagens formadas por lentes finas simples. Elas são chamadas de imagens dos casos 1, 2 e 3. As lentes convexas (convergentes) podem formar imagens reais ou virtuais (casos 1 e 2, respectivamente), enquanto as lentes côncavas (divergentes) podem formar somente imagens virtuais (sempre caso 3). As imagens reais estão sempre invertidas, mas podem ser maiores ou menores que o objeto. Por exemplo, um projetor de slides forma uma imagem maior que o slide, enquanto uma câmera torna a imagem menor do que o objeto que está sendo fotografado. As imagens virtuais estão sempre na vertical e não podem ser projetadas. As imagens virtuais são maiores do que o objeto somente no caso 2, em que uma lente convexa é usada. A imagem virtual produzida por uma lente côncava é sempre menor do que o objeto — uma imagem de caso 3. Só podemos ver e fotografar imagens virtuais usando uma lente adicional para formar uma imagem real.

Tabela\(\PageIndex{1}\): Três tipos de imagens formadas por lentes finas

Tipo	Formado quando	Tipo de imagem	\(d_i\)	m
Caso 1	positivo f\(d_0>f\)	real	\ (d_i\) ">positivo	negativo
Caso 2	positivo f\(d_0<f\)	virtual	\ (d_i\) ">negativo	positivo m > 1
Caso 3	negativo f	virtual	\ (d_i\) ">negativo	positivo

Em “Formação de imagem por espelhos”, veremos que os espelhos podem formar exatamente os mesmos tipos de imagens que as lentes.

EXPERIÊNCIA PARA LEVAR PARA CASA: CONCENTRAÇÃO DA LUZ SOLAR

Encontre várias lentes e determine se elas são convergentes ou divergentes. Em geral, aqueles que são mais grossos perto das bordas são divergentes e aqueles que são mais grossos perto do centro estão convergindo. Em um dia ensolarado, leve as lentes convergentes para fora e tente focar a luz do sol em um pedaço de papel. Determine as distâncias focais das lentes. Tenha cuidado porque o papel pode começar a queimar, dependendo do tipo de lente que você selecionou.

Estratégias de resolução de problemas para lentes

• Etapa 1. Examine a situação para determinar se a formação da imagem por uma lente está envolvida.
• Etapa 2. Determine se o traçado de raios, as equações de lente fina ou ambas devem ser empregadas. Um esboço é muito útil mesmo que o traçado de raios não seja especificamente exigido pelo problema. Escreva símbolos e valores no esboço.
• Etapa 3. Identifique exatamente o que precisa ser determinado no problema (identifique as incógnitas).
• Etapa 4. Faça uma lista do que é dado ou pode ser inferido do problema conforme declarado (identifique os conhecidos). É útil determinar se a situação envolve uma imagem do caso 1, 2 ou 3. Embora sejam apenas nomes para tipos de imagens, eles têm certas características (dadas na tabela) que podem ser de grande utilidade na solução de problemas.
• Etapa 5. Se o traçado de raios for necessário, use as regras de traçado de raios listadas no início desta seção.
• Etapa 6. A maioria dos problemas quantitativos requer o uso de equações de lentes finas. Eles são resolvidos da maneira usual, substituindo conhecidos e resolvendo incógnitos. Vários exemplos trabalhados servem como guias.
• Etapa 7. Verifique se a resposta é razoável: Faz sentido? Se você identificou o tipo de imagem (caso 1, 2 ou 3), avalie se sua resposta é consistente com o tipo de imagem, ampliação e assim por diante.

ALERTA DE EQUÍVOCO

Não percebemos que os raios de luz vêm de todas as partes do objeto, passando por todas as partes da lente, e todos podem ser usados para formar a imagem final. Geralmente sentimos que toda a lente, ou espelho, é necessária para formar uma imagem. Na verdade, meia lente formará a mesma imagem, embora mais fraca.

Resumo

• Os raios de luz que entram em uma lente convergente paralelamente ao seu eixo se cruzam em um único ponto no lado oposto.
• Para uma lente convergente, o ponto focal é o ponto em que os raios de luz convergentes se cruzam; para uma lente divergente, o ponto focal é o ponto do qual os raios de luz divergentes parecem se originar.
• A distância do centro da lente até seu ponto focal é chamada de distância focal\(f\).
• A potência\(P\) de uma lente é definida como sendo o inverso de sua distância focal,\(P = \frac{1}{f}\).
• Uma lente que faz com que os raios de luz se afastem de seu eixo é chamada de lente divergente.
• O traçado de raios é a técnica de determinar graficamente os caminhos que os raios de luz percorrem.
• A imagem na qual os raios de luz de um ponto do objeto realmente se cruzam no local da imagem e podem ser projetados em uma tela, em um pedaço de filme ou na retina de um olho é chamada de imagem real.
• As equações de lentes finas são\(\frac{1}{d_{o}} + \frac{1}{d_{1}} = \frac{1}{f}\) e\(\frac{h_{1}}{h_{o}} = m\) (ampliação).
• A distância da imagem do centro da lente é chamada de distância da imagem.
• Uma imagem que está do mesmo lado da lente que o objeto e não pode ser projetada em uma tela é chamada de imagem virtual.

Glossário

lente convergente

uma lente convexa na qual os raios de luz que entram nela paralelamente ao seu eixo convergem em um único ponto no lado oposto

lente divergente

uma lente côncava na qual os raios de luz que entram nela paralelamente ao seu eixo se afastam (divergem) de seu eixo

ponto focal

para uma lente ou espelho convergente, o ponto em que os raios de luz convergentes se cruzam; para uma lente ou espelho divergente, o ponto a partir do qual os raios de luz divergentes parecem se originar

distância focal

distância do centro de uma lente ou espelho curvo até seu ponto focal

ampliação

relação entre a altura da imagem e a altura do objeto

poder

inverso da distância focal

imagem real

imagem que pode ser projetada

imagem virtual

imagem que não pode ser projetada