23.2: Reatância, indutiva e capacitiva
- Page ID
- 195090
Objetivos de
Ao final desta seção, você poderá:
- Esboce tensão e corrente versus tempo em circuitos indutivos, capacitivos e resistivos simples.
- Calcule a reatância indutiva e capacitiva.
- Calcule a corrente e/ou tensão em circuitos indutivos, capacitivos e resistivos simples.
Muitos circuitos também contêm capacitores e indutores, além de resistores e uma fonte de tensão AC. Vimos como capacitores e indutores respondem à tensão DC quando ela é ligada e desligada. Agora vamos explorar como indutores e capacitores reagem à tensão CA senoidal.
Indutores e reatância indutiva
Suponha que um indutor esteja conectado diretamente a uma fonte de tensão CA, conforme mostrado na Figura. É razoável supor uma resistência insignificante, pois na prática podemos tornar a resistência de um indutor tão pequena que tenha um efeito insignificante no circuito. Também é mostrado um gráfico de tensão e corrente em função do tempo.
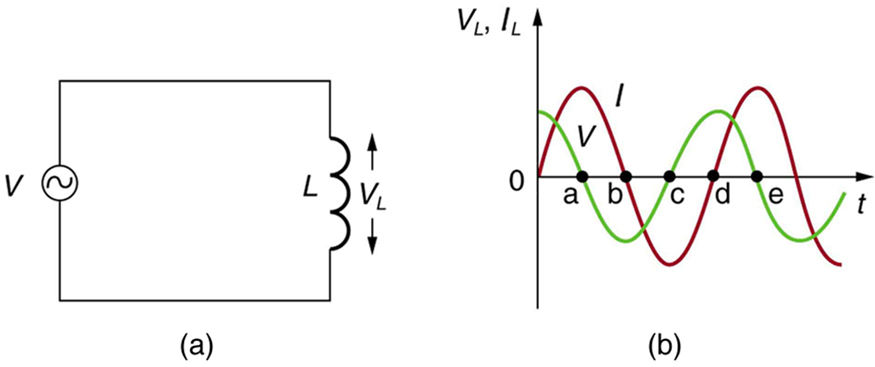
O gráfico na Figura (b) começa com a tensão no máximo. Observe que a corrente começa em zero e sobe até seu pico após a tensão que a aciona, assim como foi o caso quando a tensão DC foi ligada na seção anterior. Quando a tensão se torna negativa no ponto a, a corrente começa a diminuir; ela se torna zero no ponto b, onde a tensão é a mais negativa. A corrente então se torna negativa, novamente seguindo a tensão. A tensão se torna positiva no ponto c e começa a tornar a corrente menos negativa. No ponto d, a corrente passa por zero assim que a tensão atinge seu pico positivo para iniciar outro ciclo. Esse comportamento é resumido da seguinte forma:
Tensão AC em um indutor
Quando uma tensão senoidal é aplicada a um indutor, a tensão conduz a corrente em um quarto de um ciclo ou por um ângulo de\(90^o\) fase.
A corrente fica atrás da tensão, pois os indutores se opõem à mudança na corrente. A mudança de corrente induz um emf reverso\(V = -L(\Delta I/\Delta t)\). Isso é considerado uma resistência efetiva do indutor à corrente alternada. A corrente de braço\(I\) através de um indutor\(L\) é dada por uma versão da lei de Ohm: vo
\[I = \dfrac{V}{X_L},\]onde\(V\) está a tensão rms no indutor e\(X_L\) é definida como sendo\[X_L = 2\pi fL,\] com\(f\) a frequência da fonte de tensão CA em hertz (uma análise do circuito usando a regra de loop e o cálculo de Kirchhoff realmente produz essa expressão). \(X_L\)é chamada de reatância indutiva, porque o indutor reage para impedir a corrente. \(X_L\)tem unidades de ohms (\(1 \, H = 1 \, \Omega \cdot s\), de modo que a frequência vezes a indutância tem unidades de (ciclos/s)\((\Omega \cdot s) = \Omega\)), consistentes com seu papel como uma resistência efetiva. Faz sentido que\(X_L\) seja proporcional a\(L\), pois quanto maior a indução, maior sua resistência à mudança. Também é razoável que\(X_L\) seja proporcional à frequência\(f\), pois maior frequência significa maior mudança na corrente. Ou seja,\(\Delta I/\Delta t\) é grande para frequências grandes (grandes\(f\), pequenas\(\Delta t\)). Quanto maior a mudança, maior a oposição de um indutor.
Exemplo\(\PageIndex{1}\): Calculating Inductive Reactance and then Current
(a) Calcule a reatância indutiva de um indutor de 3,00 mH quando forem aplicadas tensões CA de 60,0 Hz e 10,0 kHz. (b) Qual é a corrente rms em cada frequência se a tensão rms aplicada for 120 V?
Estratégia
A reatância indutiva é encontrada diretamente da expressão\(X_L = 2\pi fL\). Uma vez\(X_L\) encontrada em cada frequência, a lei de Ohm, conforme declarada na Equação,\(I = V/X_L\) pode ser usada para encontrar a corrente em cada frequência.
Solução para (a)
Inserir a frequência e a indutância na Equação\(X_L = 2\pi fL\) fornece
\[X_L = 2\pi fL = 6.28(60.0/s)(3.00 \, mH) = 1.13 \, \Omega \, at \, 60 \, Hz.\]
Da mesma forma, a 10 kHz,
\[X_L = 2\pi fL = 6.28(1.00 \times 10^4/s)(3.00 \, mH) = 188 \, \Omega \, at \, 10 \, kHz.\]
Solução para (b)
A corrente rms agora é encontrada usando a versão da lei de Ohm na Equação\(I = V/X_L\), dado que a tensão rms aplicada é de 120 V. Para a primeira frequência, isso produz
\[I = \dfrac{V}{X_L} = \dfrac{120 \, V}{1.13 \, \Omega} = 106 \, A \, at \, 60 \, Hz.\]
Da mesma forma, a 10 kHz,
\[I = \dfrac{V}{X_L} = \dfrac{120 \, V}{188 \, \Omega} = 0.637 \, A \, at \, 10 \, kHz.\]
Discussão
O indutor reage de forma muito diferente nas duas frequências diferentes. Na frequência mais alta, sua reatância é grande e a corrente é pequena, consistente com a forma como um indutor impede mudanças rápidas. Assim, as altas frequências são as mais impedidas. Os indutores podem ser usados para filtrar altas frequências; por exemplo, um indutor grande pode ser colocado em série com um sistema de reprodução de som ou em série com seu computador doméstico para reduzir a saída de som de alta frequência dos alto-falantes ou picos de energia de alta frequência no computador.
Observe que, embora a resistência no circuito considerado seja insignificante, a corrente CA não é extremamente grande porque a reatância indutiva impede seu fluxo. Com o AC, não há tempo para que a corrente fique extremamente grande.
Capacitores e reatância capacitiva
Considere o capacitor conectado diretamente a uma fonte de tensão AC, conforme mostrado na Figura. A resistência de um circuito como esse pode ser tão pequena que tenha um efeito insignificante em comparação com o capacitor e, portanto, podemos assumir uma resistência insignificante. A tensão no capacitor e a corrente são representadas graficamente como funções do tempo na figura.
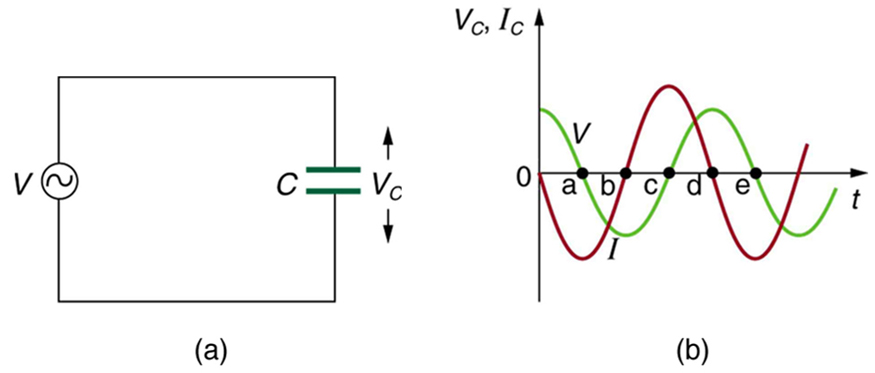
O gráfico na Figura começa com a tensão no máximo no capacitor. A corrente é zero neste ponto, porque o capacitor está totalmente carregado e interrompe o fluxo. Em seguida, a tensão cai e a corrente fica negativa à medida que o capacitor é descarregado. No ponto a, o capacitor está totalmente descarregado (\(Q = 0\)nele) e a tensão é zero. A corrente permanece negativa entre os pontos a e b, fazendo com que a tensão no capacitor seja revertida. Isso é concluído no ponto b, onde a corrente é zero e a tensão tem seu valor mais negativo. A corrente se torna positiva após o ponto b, neutralizando a carga no capacitor e levando a tensão a zero no ponto c, o que permite que a corrente alcance seu máximo. Entre os pontos c e d, a corrente cai para zero à medida que a tensão sobe até seu pico e o processo começa a se repetir. Durante todo o ciclo, a tensão segue o que a corrente está fazendo em um quarto de um ciclo:
Tensão AC em um capacitor
Quando uma tensão senoidal é aplicada a um capacitor, a tensão segue a corrente em um quarto de um ciclo ou por um ângulo de fase.
O capacitor está afetando a corrente, tendo a capacidade de pará-la completamente quando totalmente carregado. Como uma tensão AC é aplicada, há uma corrente rms, mas ela é limitada pelo capacitor. Isso é considerado uma resistência efetiva do capacitor à corrente alternada e, portanto, a corrente rms no circuito contendo apenas um capacitor\(I\) é dada por outra versão da lei de Ohm como sendo
\[I = \dfrac{V}{X_C},\]onde\(V\) está a tensão rms e\(X_C\) é definida (como acontece com\(X_L\), esta expressão para\(X_C\) resultados de uma análise do circuito usando as regras e o cálculo de Kirchhoff) como sendo
\[X_C = \dfrac{1}{2\pi fC},\]onde\(X_C\) é chamada de reatância capacitiva, porque o capacitor reage para impedir a corrente. \(X_C\)tem unidades de ohms (verificação deixada como um exercício para o leitor). \(X_C\)é inversamente proporcional à capacitância\(C\), quanto maior o capacitor, maior a carga que ele pode armazenar e maior a corrente que pode fluir. Também é inversamente proporcional à frequência\(f\), quanto maior a frequência, menos tempo há para carregar totalmente o capacitor e, portanto, impede menos a corrente.
Exemplo \(\PageIndex{2}\): Calculating Capacitive Reactance and then Current
(a) Calcule a reatância capacitiva de um capacitor de 5,00 mF quando as tensões CA de 60,0 Hz e 10,0 kHz forem aplicadas. (b) Qual é a corrente rms se a tensão rms aplicada for 120 V?
Estratégia
A reatância capacitiva é encontrada diretamente da expressão em\(X_C = \frac{1}{2\pi fC}\). Uma\(X_C\) vez encontrada em cada frequência, a lei de Ohm declarou como\(I = V/X_C\)
pode ser usado para encontrar a corrente em cada frequência.
Solução para (a)
Inserindo a frequência e a capacitância em\(X_C = \frac{1}{2\pi fC}\) dá
\[X_C = \dfrac{1}{2\pi fC}\]
\[= \dfrac{1}{6.28(60.0/s)(5.00 \, \mu F)} = 531 \, \Omega \, at \, 60 \, Hz.\]
Da mesma forma, a 10 kHz,
\[X_C = \dfrac{1}{2\pi fC} = \dfrac{1}{6.28(1.00 \times 10^4/s)(5.00 \, \mu F)}.\]
\[= 3.18 \, \Omega \, at \, 10 \, kHz\]
Solução para (b)
A corrente rms agora é encontrada usando a versão da lei de Ohm em\(I = V/X_C\), dado que a tensão rms aplicada é de 120 V. Para a primeira frequência, isso produz
\[I = \dfrac{V}{X_C} = \dfrac{120 \, V}{531 \, \Omega} = 0.226 \, A \, at \, 60 \, Hz.\]
Da mesma forma, a 10 kHz,
\[I = \dfrac{V}{X_C} = \dfrac{120 \, V}{3.18 \, \Omega} = 37.7 \, A \, at \, 10 \, kHz.\]
Discussão
O capacitor reage de maneira muito diferente nas duas frequências diferentes e exatamente da maneira oposta que um indutor reage. Na frequência mais alta, sua reatância é pequena e a corrente é grande. Os capacitores favorecem a mudança, enquanto os indutores se opõem à mudança. Os capacitores são os que mais impedem as baixas frequências, pois a baixa frequência permite que eles tenham tempo de carregar e interromper a corrente. Capacitores podem ser usados para filtrar baixas frequências. Por exemplo, um capacitor em série com um sistema de reprodução de som o livra do zumbido de 60 Hz.
Embora um capacitor seja basicamente um circuito aberto, há uma corrente rms em um circuito com uma tensão CA aplicada a um capacitor. Isso ocorre porque a tensão está continuamente revertendo, carregando e descarregando o capacitor. Se a frequência for zero (DC),\(X_C\) tende ao infinito e a corrente é zero quando o capacitor é carregado. Em frequências muito altas, a reatância do capacitor tende a zero — ele tem uma reatância insignificante e não impede a corrente (ele age como um simples fio). Os capacitores têm o efeito oposto nos circuitos de corrente alternada que os indutores.
Resistores em um circuito AC
Apenas como um lembrete, considere a Figura, que mostra uma tensão CA aplicada a um resistor e um gráfico de tensão e corrente em relação ao tempo. A tensão e a corrente estão exatamente em fase em um resistor. Não há dependência de frequência do comportamento da resistência simples em um circuito:
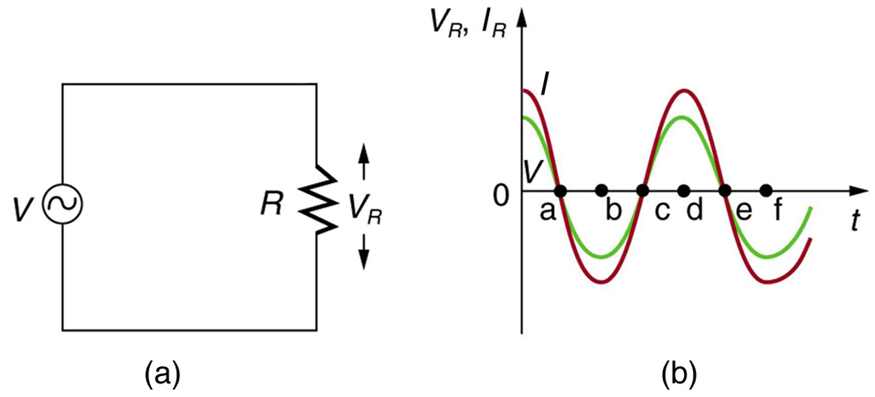
Tensão AC em um resistor
Quando uma tensão senoidal é aplicada a um resistor, a tensão está exatamente em fase com a corrente — eles têm um ângulo de\(0^o\) fase.
Resumo
- Para indutores em circuitos de corrente alternada, descobrimos que quando uma tensão senoidal é aplicada a um indutor, a tensão conduz a corrente em um quarto de um ciclo ou por um ângulo de\(90^o\) fase.
- A oposição de um indutor a uma mudança na corrente é expressa como um tipo de resistência AC.
- A lei de Ohm para um indutor\(V\) é\[ I = \dfrac{V}{X_L},\] onde está a tensão rms no indutor.
- \(X_L\)é definida como sendo a reatância indutiva, dada por\[X_L = 2\pi fL,\] com\(f\) a frequência da fonte de tensão AC em hertz.
- A reatância indutiva\(X_L\) tem unidades de ohms e é maior em altas frequências.
- Para capacitores, descobrimos que quando uma tensão senoidal é aplicada a um capacitor, a tensão segue a corrente em um quarto de um ciclo ou por um ângulo de\(90^o\) fase.
- Como um capacitor pode interromper a corrente quando totalmente carregado, ele limita a corrente e oferece outra forma de resistência CA; a lei de Ohm para um capacitor\(V\) é\[I = \dfrac{V}{X_C},\] onde está a tensão rms no capacitor.
- \(X_C\)é definida como sendo a reatância capacitiva, dada por\[X_C = \dfrac{1}{2\pi fC}.\]
- \(X_C\)tem unidades de ohms e é maior em baixas frequências.
Glossário
- reatância indutiva
- a oposição de um indutor a uma mudança na corrente; calculado por\(X_L = 2\pi fL\)
- reatância capacitiva
- a oposição de um capacitor a uma mudança na corrente; calculado por\(X_C = \frac{1}{2\pi fC}\)
Colaboradores


