23.1: Circuitos RL

Objetivos de

Ao final desta seção, você poderá:

• Calcule a corrente em um circuito RL após um número especificado de intervalos de tempo característicos.
• Calcule o tempo característico de um circuito RL.
• Esboce a corrente em um circuito RL ao longo do tempo.

Sabemos que a corrente através de um indutor\(L\) não pode ser ligada ou desligada instantaneamente. A mudança na corrente muda o fluxo, induzindo um emf que se opõe à mudança (lei de Lenz). Quanto tempo dura a oposição? A corrente fluirá e poderá ser desligada, mas quanto tempo demora? \(\PageIndex{1}\)A figura mostra um circuito de comutação que pode ser usado para examinar a corrente por meio de um indutor em função do tempo.

Figura\(\PageIndex{1}\): (a) Um circuito RL com um interruptor para ligar e desligar a corrente. Quando na posição 1, a bateria, o resistor e o indutor estão em série e uma corrente é estabelecida. Na posição 2, a bateria é removida e a corrente acaba parando devido à perda de energia no resistor. (b) Um gráfico do crescimento atual em relação ao tempo em que a chave é movida para a posição 1. (c) Um gráfico da queda de corrente quando o interruptor é movido para a posição 2.

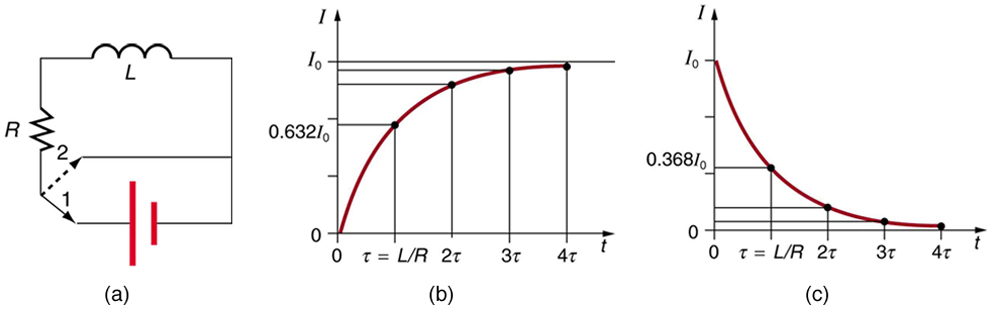
Quando o interruptor é movido pela primeira vez para a posição 1 (at\(t = 0\)), a corrente é zero e eventualmente sobe\(I_0 = V/R\) para. onde\(R\) está a resistência total do circuito. A oposição do indutor\(L\) é maior no início, porque a quantidade de mudança é maior. A oposição que ela representa está na forma de um emf induzido, que diminui para zero à medida que a corrente se aproxima de seu valor final. O emf oposto é proporcional à quantidade de mudança restante. Essa é a marca registrada de um comportamento exponencial e pode ser mostrado com o cálculo de que

\[I = I_0(1 - e^{-t./\tau}) \, (turning \, on),\]

é a corrente em um circuito RL quando ligado (observe a semelhança com o comportamento exponencial da tensão em um capacitor de carregamento). A corrente inicial é zero e se aproxima\(I_0 = V/R\) com uma constante de tempo característica\(\tau\) para um circuito RL, dada por

\[\tau = \dfrac{L}{R},\]

onde\(\tau\) tem unidades de segundos, desde\(1 \, H = 1 \, \Omega \cdot s\). No primeiro período de tempo\(\tau\), a corrente sobe de zero para\(0.632 \, I_0\), já que

\[I = I_0(1 - e^{-1}) = I_0 (1 - 0.368) = 0.632 \, I_0.\]

A corrente será de 0,632 do restante na próxima vez\(\tau\). Uma propriedade bem conhecida do exponencial é que o valor final nunca é exatamente alcançado, mas 0,632 do restante desse valor é alcançado em cada tempo característico\(\tau\). Em apenas alguns múltiplos do tempo\(\tau\), o valor final está quase alcançado, como\(\PageIndex{1b}\) ilustra o gráfico na Figura.

O tempo característico\(\tau\) depende de apenas dois fatores, a indutância\(L\) e a resistência\(R\). Quanto maior a indutância\(L\), maior\(\tau\) é, o que faz sentido, pois uma grande indutância é muito eficaz na oposição à mudança. Quanto menor a resistência\(R\), maior\(\tau\) é. Novamente, isso faz sentido, pois uma pequena resistência significa uma grande corrente final e uma mudança maior para chegar lá. Em ambos os casos, grandes\(L\) e pequenos,\(R\) mais energia é armazenada no indutor e é necessário mais tempo para entrar e sair.

Quando o interruptor na Figura\(\PageIndex{1a}\) é movido para a posição 2 e corta a bateria do circuito, a corrente cai devido à dissipação de energia pelo resistor. Mas isso também não é instantâneo, já que o indutor se opõe à diminuição da corrente induzindo um emf na mesma direção da bateria que acionou a corrente. Além disso, há uma certa quantidade de energia\((1/2)LI_0^2\), armazenada no indutor, e ela é dissipada a uma taxa finita. À medida que a corrente se aproxima de zero, a taxa de diminuição diminui, já que a taxa de dissipação de energia é\(I^2R\). Mais uma vez, o comportamento é exponencial e\(I\) é considerado

\[I = I_0e^{-t/\tau} \, (turning \, off).\]

(Figura\(\PageIndex{1c}\)) No primeiro período de tempo\(\tau = L/R\) após o fechamento do interruptor, a corrente cai para 0,368 de seu valor inicial, desde então\(I = I_0e^{-1} = 0.368 \, I_0\). Em cada tempo sucessivo,\(\tau\) a corrente cai para 0,368 do valor anterior e, em alguns múltiplos de\(\tau\), a corrente se torna muito próxima de zero, conforme visto no gráfico da Figura\(\PageIndex{1c}\).

Exemplo\(\PageIndex{1}\): Calculating Characteristic Time and Current in an RL Circuit

1. Qual é a constante de tempo característica para um indutor de 7,50 mH em série com um\(3.00 \, \Omega\) resistor?
2. Encontre a corrente de 5,00 ms após o interruptor ser movido para a posição 2 para desconectar a bateria, se ela for inicialmente 10,0 A.

Estratégia para (a)

A constante de tempo para um circuito RL é definida por\(\tau = L/R\).

Solução para (a)

Inserir valores conhecidos na expressão de\(\tau\) dado em\(\tau = L/R\) rendimentos

\[\begin{align*} \tau &= \dfrac{L}{R} \\[5pt] &= \dfrac{7.50 \, mH}{3.00 \, \Omega} \\[5pt] &= 2.50 \, ms. \end{align*}\]

Discussão para (a)

Este é um tempo pequeno, mas definitivamente finito. A bobina estará muito próxima de sua corrente total em cerca de dez constantes de tempo, ou cerca de 25 ms.

Estratégia para (b)

Podemos encontrar a corrente usando\(I = I_0 e^{-t/\tau}\) ou considerando o declínio nas etapas. Como o tempo é o dobro do tempo característico, consideramos o processo em etapas.

Solução para (b)

Nos primeiros 2,50 ms, a corrente diminui para 0,368 de seu valor inicial, que é

\[\begin{align*} I &= 0.368 \, I_0 \\[5pt] &= (0.368)(10.0 \, A)\\[5pt] &= 3.68 \, A \, @ \, t = 2.50 \, ms.\end{align*}\]

Depois de mais 2,50 ms, ou um total de 5,00 ms, a corrente diminui para 0,368 do valor que acabamos de encontrar. Ou seja,

\[\begin{align*} I' &= 0.368 \, I \\[5pt] &= (0.368)(3.68 \, A)\\[5pt] &= 1.35 \, A \, @ \, t = 5.00 \, ms.\end{align*}\]

Discussão para (b)

Depois de passarem mais 5,00 ms, a corrente será de 0,183 A (veja o Exercício); portanto, embora desapareça, a corrente certamente não chega a zero instantaneamente.

Em resumo, quando a tensão aplicada a um indutor é alterada, a corrente também muda, mas a mudança na corrente atrasa a mudança na tensão em um circuito RL. Em Reatância, Indutiva e Capacitiva, exploramos como um circuito RL se comporta quando uma tensão CA senoidal é aplicada.

Resumo

• Quando uma conexão em série de um resistor e um indutor - um circuito RL - é conectada a uma fonte de tensão, a variação de tempo da corrente é\[I - I_0(1 - e^{-t/\tau}) \, (turning \, on),\] onde\(I_0 = V/R\) está a corrente final.
• A constante de tempo característica\(\tau\) é\(tau = \frac{L}{R}\), onde\(L\) está a indutância e\(R\) é a resistência.
• Na primeira constante de tempo,\(\tau\) a corrente sobe de zero para\(0.632 \, I_0\), e 0,632 do restante em cada intervalo de tempo subsequente\(\tau\).
• Quando o indutor sofre um curto-circuito através de um resistor, a corrente diminui, pois\[I = I_0 e^{-t/\tau} \, turning \, off).\] Aqui\(I_0\) está a corrente inicial.
• A corrente cai para\(0.368 \, I_0\) no primeiro intervalo\(\tau\) de tempo e 0,368 do restante para zero em cada tempo subsequente\(\tau\).

Glossário

constante de tempo característica

denotado por\(\tau\), de uma série específica, o circuito RL é calculado por\(\tau = \frac{L}{R}\), onde\(L\) está a indutância e\(R\) é a resistência