Skip to main content
Global

22.9: Campos magnéticos produzidos por correntes - Lei de Ampere

  1. Last updated
  2. Save as PDF
  • Page ID
    194578

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Calcule a corrente que produz um campo magnético.
    • Use a regra 2 da mão direita para determinar a direção da corrente ou a direção dos ciclos do campo magnético.

    Quanta corrente é necessária para produzir um campo magnético significativo, talvez tão forte quanto o campo da Terra? Os topógrafos dirão que as linhas aéreas de energia elétrica criam campos magnéticos que interferem nas leituras da bússola. De fato, quando Oersted descobriu em 1820 que uma corrente em um fio afetava a agulha de uma bússola, ele não estava lidando com correntes extremamente grandes. Como a forma dos fios que transportam corrente afeta a forma do campo magnético criado? Observamos anteriormente que um circuito de corrente criou um campo magnético semelhante ao de uma barra magnética, mas que tal um fio reto ou um toróide (donut)? Como a direção de um campo criado pela corrente está relacionada à direção da corrente? As respostas a essas perguntas são exploradas nesta seção, juntamente com uma breve discussão sobre a lei que rege os campos criados pelas correntes.

    Campo magnético criado por um longo fio transportador de corrente reta: regra 2 da mão direita

    Os campos magnéticos têm direção e magnitude. Conforme observado anteriormente, uma maneira de explorar a direção de um campo magnético é com bússolas, conforme mostrado para um longo fio transportador de corrente reta na Figura\(\PageIndex{1}\). As sondas Hall podem determinar a magnitude do campo. O campo ao redor de um fio longo e reto é encontrado em laços circulares. A regra 2 da mão direita (RHR-2) emerge dessa exploração e é válida para qualquer segmento atual — aponte o polegar na direção da corrente e os dedos se curvam na direção das alças do campo magnético criadas por ela.

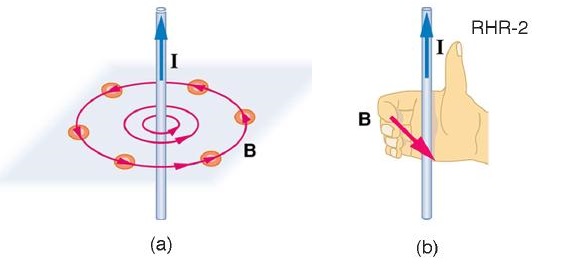
    A Figura a mostra um fio orientado verticalmente com a corrente I correndo de baixo para cima. As linhas do campo magnético circulam o fio no sentido anti-horário, visto de cima. A Figura b ilustra a regra 2 da mão direita. O polegar aponta para cima com a corrente I. Os dedos se curvam no sentido anti-horário, vistos de cima.
    Figura\(\PageIndex{1}\): (a) As bússolas colocadas perto de um longo fio transportador de corrente reta indicam que as linhas de campo formam laços circulares centrados no fio. (b) A regra 2 da mão direita afirma que, se o polegar direito apontar na direção da corrente, os dedos se curvam na direção do campo. Essa regra é consistente com o campo mapeado para o fio reto longo e é válida para qualquer segmento atual.

    A intensidade do campo magnético (magnitude) produzida por um longo fio transportador de corrente reta é considerada por experimento como

    \[B = \underbrace{\frac{\mu_{0}I}{2\pi r}}_{\text{long straight wire }},\label{22.10.1}\]

    onde\(I\) está a corrente,\(r\) é a menor distância até o fio e a constante\(\mu_{0} = 4\pi \times 10^{-7} T \cdot m/A\) é a permeabilidade do espaço livre. (\(\mu_{0}\)é uma das constantes básicas da natureza. Veremos mais tarde o que\(\mu_{0}\) está relacionado à velocidade da luz.) Como o fio é muito longo, a magnitude do campo depende apenas da distância do fio\(r\), não da posição ao longo do fio.

    Exemplo\(\PageIndex{1}\): Calculating Current that Produces a Magnetic Field

    Encontre a corrente em um fio longo e reto que produziria um campo magnético com o dobro da força da Terra a uma distância de 5,0 cm do fio.

    Estratégia:

    O campo da Terra é de cerca de\(5.0 \times 10^{-5} T\), então aqui,\(B\) devido ao fio, é considerado\(1.0 \times 10^{-4} T\). A equação\(B = \frac{\mu_{0}I}{2\pi r}\) pode ser usada para encontrar\(I\), já que todas as outras quantidades são conhecidas.

    Solução

    Resolver\(I\) e inserir valores conhecidos fornece

    \[ \begin{align*} I &= \frac{2 \pi r B}{\mu_{0}} \\[5pt] &= \frac{2\pi \left(5.0 \times 10^{-2} m \right) \left(1.0 \times 10^{-4}\right)}{4\pi \times 10^{-7} T \cdot m / A} \\[5pt] &= 25 A. \end{align*} \]

    Discussão:

    Portanto, uma corrente moderadamente grande produz um campo magnético significativo a uma distância de 5,0 cm de um longo fio reto. Observe que a resposta é declarada com apenas dois dígitos, já que o campo da Terra é especificado para apenas dois dígitos neste exemplo.

    Lei de Ampere e outras

    O campo magnético de um fio longo e reto tem mais implicações do que você imagina à primeira vista. Cada segmento de corrente produz um campo magnético como o de um longo fio reto, e o campo total de qualquer forma de corrente é a soma vetorial dos campos devidos a cada segmento. A declaração formal da direção e magnitude do campo devido a cada segmento é chamada de Lei Biot-Savart. O cálculo integral é necessário para somar o campo de uma corrente de forma arbitrária. Isso resulta em uma lei mais completa, chamada Lei de Ampere, que relaciona o campo magnético e a corrente de uma forma geral. A lei de Ampere, por sua vez, faz parte das equações de Maxwell, que fornecem uma teoria completa de todos os fenômenos eletromagnéticos. Considerações sobre como as equações de Maxwell aparecem para diferentes observadores levaram à moderna teoria da relatividade e à constatação de que os campos elétrico e magnético são manifestações diferentes da mesma coisa. A maior parte disso está além do escopo deste texto, tanto no nível matemático, que requer cálculo, quanto na quantidade de espaço que pode ser dedicado a ele. Mas para o estudante interessado, e particularmente para aqueles que continuam em física, engenharia ou atividades similares, aprofundar esses assuntos revelará descrições da natureza que são elegantes e profundas. Neste texto, devemos ter em mente as características gerais, como RHR-2 e as regras para linhas de campo magnético listadas em 22.4, enquanto nos concentramos nos campos criados em determinadas situações importantes.

    FAZENDO CONEXÕES: RELATIVIDADE:

    Ouvindo tudo o que fazemos sobre Einstein, às vezes temos a impressão de que ele inventou a relatividade do nada. Pelo contrário, uma das motivações de Einstein era resolver dificuldades em saber como diferentes observadores veem os campos magnéticos e elétricos.

    Campo magnético produzido por um circuito circular transportador de corrente

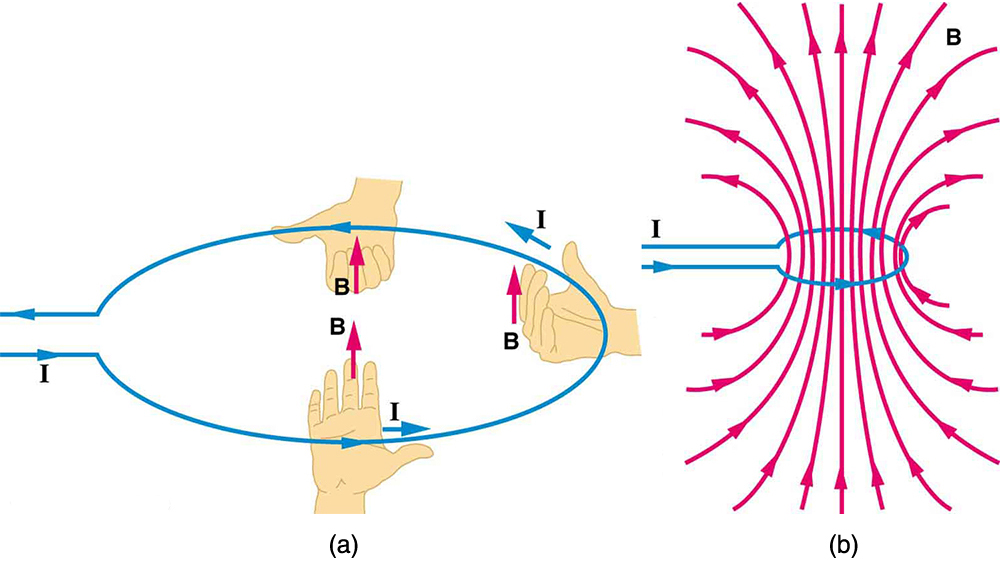
    O campo magnético próximo a um circuito de fio transportador de corrente é mostrado na Figura\(\PageIndex{2}\). Tanto a direção quanto a magnitude do campo magnético produzido por um circuito transportador de corrente são complexas. O RHR-2 pode ser usado para fornecer a direção do campo próximo ao loop, mas o mapeamento com bússolas e as regras sobre as linhas de campo fornecidas na Seção 22.4 são necessários para obter mais detalhes. Existe uma fórmula simples para a intensidade do campo magnético no centro de um circuito circular. É

    \[B = \frac{\mu_{0}I}{2R}\left(at \quad center \quad of \quad loop\right),\label{22.10.3}\]

    onde\(R\) está o raio do loop. Essa equação é muito semelhante à de um fio reto, mas é válida somente no centro de um laço circular de arame. A semelhança das equações indica que uma intensidade de campo semelhante pode ser obtida no centro de um loop. Uma forma de obter um campo maior é ter\(N\) loops; então, o campo é\(B = N \mu_{0} I / \left(2R\right)\). Observe que quanto maior o loop, menor o campo no centro, porque a corrente está mais distante.

    A Figura a ilustra o uso da regra 2 da mão direita para determinar a direção do campo magnético em torno de um circuito transportador de corrente. O polegar direito aponta na direção de I enquanto os dedos se curvam na direção de B. A Figura b mostra as linhas do campo magnético circulando o fio, vistas de lado.
    Figura\(\PageIndex{2}\): (a) O RHR-2 fornece a direção do campo magnético dentro e fora de um circuito transportador de corrente. (b) Um mapeamento mais detalhado com bússolas ou com uma sonda Hall completa a imagem. O campo é semelhante ao de uma barra magnética.

    Campo magnético produzido por um solenóide transportador de corrente

    Um solenóide é uma longa bobina de fio (com muitas voltas ou voltas, em oposição a um laço plano). Devido à sua forma, o campo dentro de um solenóide pode ser muito uniforme e também muito forte. O campo do lado de fora das bobinas é quase zero. A figura\(\PageIndex{3}\) mostra a aparência do campo e como sua direção é dada pelo RHR-2.

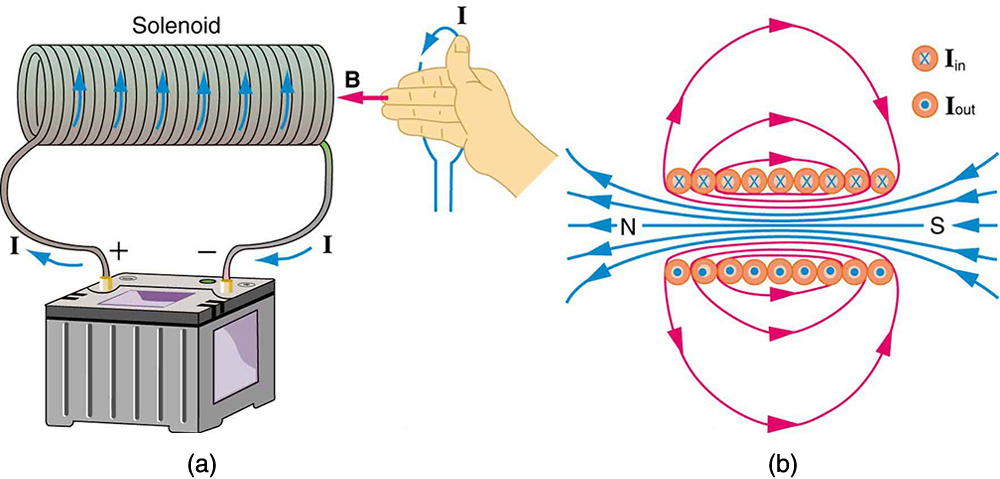
    Um diagrama de um solenóide. A corrente sobe da bateria no lado esquerdo e gira em espiral com o fio solenóide, de forma que a corrente sobe nas seções frontais do solenóide e depois desce na parte traseira. Uma ilustração da regra 2 da mão direita mostra o polegar apontando para cima na direção da corrente e os dedos se curvando na direção do campo magnético. Um corte longitudinal do solenóide mostra linhas de campo magnético densamente compactadas e indo do pólo sul ao pólo norte, através do solenóide. As linhas externas do solenóide estão muito mais afastadas e vão do pólo norte ao redor do solenóide até o pólo sul.
    Figura\(\PageIndex{3}\): (a) Devido à sua forma, o campo dentro de um solenóide de comprimento\(l\) é notavelmente uniforme em magnitude e direção, conforme indicado pelas linhas de campo retas e uniformemente espaçadas. O campo fora das bobinas é quase zero. (b) Este corte mostra o campo magnético gerado pela corrente no solenóide.

    O campo magnético dentro de um solenóide transportador de corrente é muito uniforme em direção e magnitude. Somente perto das extremidades ele começa a enfraquecer e mudar de direção. O campo externo tem complexidades semelhantes às alças planas e barras magnéticas, mas a intensidade do campo magnético dentro de um solenóide é simplesmente\[B = \mu_{0}nI \left(inside \quad a \quad solenoid\right),\label{10.22.4}\] onde\(n\) está o número de voltas por unidade de comprimento do solenóide (\(n = N/l\)\(N\)sendo o número de loops e\(l\) o comprimento). Observe que\(B\) é a intensidade do campo em qualquer lugar na região uniforme do interior e não apenas no centro. Grandes campos uniformes espalhados por um grande volume são possíveis com solenóides, como indica o exemplo.

    Exemplo\(\PageIndex{2}\):Calculating Field Strength inside a Solenoid

    Qual é o campo dentro de um solenóide de 2,00 m de comprimento que tem 2000 voltas e carrega uma corrente de 1600 A?

    Estratégia

    Para encontrar a intensidade do campo dentro de um solenóide, usamos\(B = \mu_{0}nI\). Primeiro, notamos que o número de loops por unidade de comprimento é

    \[n = \frac{N}{l} = \frac{2000}{2.00 m} = 1000m^{-1} = 10 cm^{-1}. \nonumber\]

    Solução

    A substituição de valores conhecidos fornece

    \[ \begin{align*} B &= \mu_{0}nI = \left(4\pi \times 10^{-7} T \cdot m/A\right) \left(1000 m^{-1}\right) \left(1600 A\right) \\[5pt] &= 2.01 T. \end{align*}\]

    Discussão

    Essa é uma grande intensidade de campo que pode ser estabelecida sobre um solenóide de grande diâmetro, como nos usos médicos da ressonância magnética (MRI). A corrente muito grande é uma indicação de que os campos dessa força não são facilmente alcançados, no entanto. Uma corrente tão grande através de 1000 loops espremidos em um metro de comprimento produziria um aquecimento significativo. Correntes mais altas podem ser obtidas usando fios supercondutores, embora isso seja caro. Há um limite superior para a corrente, pois o estado supercondutor é interrompido por campos magnéticos muito grandes.

    Existem variações interessantes da bobina plana e do solenóide. Por exemplo, a bobina toroidal usada para confinar as partículas reativas em tokamaks é muito parecida com um solenóide dobrado em um círculo. O campo dentro de um toróide é muito forte, mas circular. Partículas carregadas viajam em círculos, seguindo as linhas de campo, e colidem umas com as outras, talvez induzindo a fusão. Mas as partículas carregadas não cruzam as linhas do campo e escapam do toróide. Uma ampla gama de formas de bobina é usada para produzir todos os tipos de formas de campo magnético. A adição de materiais ferromagnéticos produz maior intensidade de campo e pode ter um efeito significativo na forma do campo. Os materiais ferromagnéticos tendem a capturar campos magnéticos (as linhas de campo se dobram no material ferromagnético, deixando campos mais fracos fora dele) e são usados como escudos para dispositivos afetados adversamente por campos magnéticos, incluindo o campo magnético da Terra.

    EXPLORAÇÕES PHET: GERADOR

    Gere eletricidade com uma barra magnética! Descubra a física por trás dos fenômenos explorando ímãs e como você pode usá-los para fazer uma lâmpada acender.

    Resumo

    • A força do campo magnético criado pela corrente em um fio longo e reto é dada por\[B = \frac{\mu_{0}I}{2 \pi r} \left(long \quad straight \quad wire\right), \nonumber\] onde\(I\) está a corrente,\(r\) é a menor distância até o fio e a constante\(\mu_{0} = 4\pi \times 10^{-7} T \cdot m/a\) é a permeabilidade do espaço livre.
    • A direção do campo magnético criado por um fio longo e reto é dada pela regra 2 da mão direita (RHR-2): aponte o polegar da mão direita na direção da corrente e os dedos se curvam na direção das alças do campo magnético criadas por ela.
    • O campo magnético criado pela corrente seguindo qualquer caminho é a soma (ou integral) dos campos devidos aos segmentos ao longo do caminho (magnitude e direção, como em um fio reto), resultando em uma relação geral entre corrente e campo conhecida como lei de Ampere.
    • A intensidade do campo magnético no centro de um circuito circular é dada por\[B = \frac{\mu_{0}I}{2R} \left(at \quad center \quad of \quad loop\right), \nonumber\] onde\(R\) está o raio do circuito. Essa equação se torna\(B = \mu_{0}nI/\left(2R\right)\) para uma bobina plana de\(N\) loops. O RHR-2 fornece a direção do campo em torno do loop. Uma bobina longa é chamada de solenóide.
    • A intensidade do campo magnético dentro de um solenóide\(n\) é\[B = \mu_{0}nI \left(inside \quad a \quad solenoid\right), \nonumber\] onde está o número de voltas por unidade de comprimento do solenóide. O campo interno é muito uniforme em magnitude e direção.

    Glossário

    regra 2 da mão direita (RHR-2)
    uma regra para determinar a direção do campo magnético induzido por um fio transportador de corrente: aponte o polegar da mão direita na direção da corrente e os dedos se curvam na direção dos laços do campo magnético
    intensidade do campo magnético (magnitude) produzida por um longo fio transportador de corrente reta
    definido como\(B=\frac{μ_0I}{2πr}\), onde I é a corrente,\(r\) é a menor distância até o fio e\(μ_0\) é a permeabilidade do espaço livre
    permeabilidade do espaço livre
    a medida da capacidade de um material, neste caso espaço livre, de suportar um campo magnético; a constante\(μ_0=4π×10^{−7}T⋅m/A\)
    intensidade do campo magnético no centro de um circuito circular
    definido como\(B=\frac{μ_0I}{2R}\) onde\(R\) está o raio do loop
    solenóide
    um fio fino enrolado em uma bobina que produz um campo magnético quando uma corrente elétrica passa por ele
    intensidade do campo magnético dentro de um solenóide
    definido como\(B=μ0nI\) onde\(n\) é o número de loops por unidade de comprimento do solenóide (\(n=N/l\),\(N\) sendo o número de loops e\(l\) o comprimento)
    Lei Biot-Savart
    uma lei física que descreve o campo magnético gerado por uma corrente elétrica em termos de uma equação específica
    Lei de Ampere
    a lei física que afirma que o campo magnético em torno de uma corrente elétrica é proporcional à corrente; cada segmento de corrente produz um campo magnético como o de um longo fio reto, e o campo total de qualquer forma de corrente é a soma vetorial dos campos devidos a cada segmento
    Equações de Maxwell
    um conjunto de quatro equações que descrevem fenômenos eletromagnéticos