Skip to main content
Global

22.8: Torque em um circuito de corrente - motores e medidores

  1. Last updated
  2. Save as PDF
  • Page ID
    194603

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Descreva como motores e medidores funcionam em termos de torque em um circuito de corrente.
    • Calcule o torque em um circuito de transporte de corrente em um campo magnético.

    Os motores são a aplicação mais comum de força magnética em fios transportadores de corrente. Os motores têm laços de fio em um campo magnético. Quando a corrente passa pelas alças, o campo magnético exerce torque nas alças, que giram um eixo. A energia elétrica é convertida em trabalho mecânico no processo (Figura\(\PageIndex{1}\)).

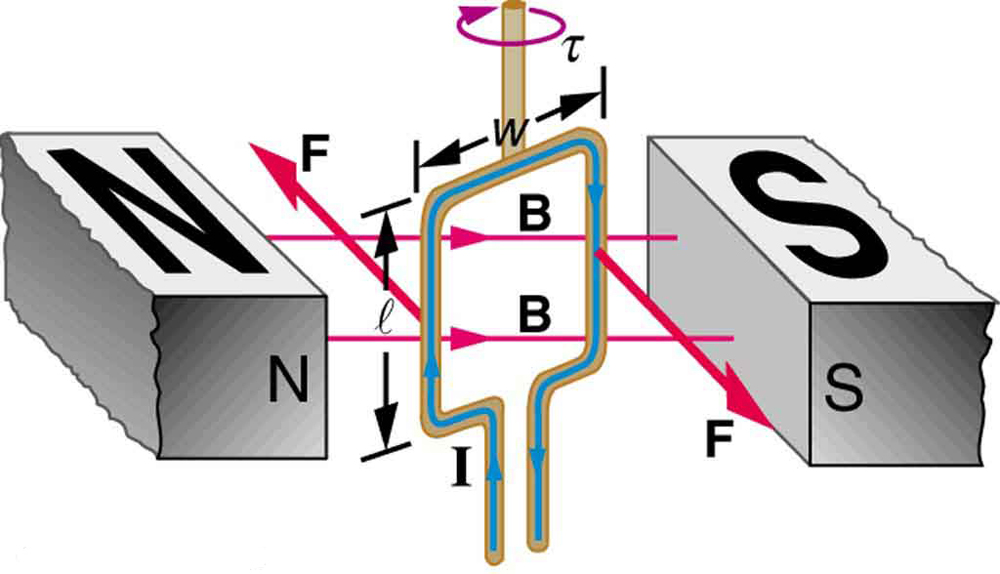
    Diagrama mostrando um circuito transportador de corrente de largura w e comprimento l entre os pólos norte e sul de um ímã. O pólo norte está à esquerda e o pólo sul está à direita do circuito. O campo magnético B vai do pólo norte através do circuito até o pólo sul. O loop é mostrado em um instante, enquanto gira no sentido horário. A corrente sobe pelo lado esquerdo do circuito, atravessa a parte superior e desce pelo lado direito. Há uma força F orientada na página no lado esquerdo do loop e uma força F orientada para fora da página no lado direito do loop. O torque no circuito é no sentido horário, conforme visto de cima.
    Figura\(\PageIndex{1}\): Torque em um circuito de corrente. Um circuito de arame transportador de corrente conectado a um eixo giratório vertical sente forças magnéticas que produzem um torque no sentido horário, visto de cima.

    Vamos examinar a força em cada segmento do circuito na Figura 1 para encontrar os torques produzidos em torno do eixo vertical. (Isso levará a uma equação útil para o torque no circuito.) Consideramos que o campo magnético é uniforme sobre o laço retangular, que tem largura\(w\) e altura\(l\). Primeiramente, notamos que as forças nos segmentos superior e inferior são verticais e, portanto, paralelas ao eixo, sem produzir torque. Essas forças verticais são iguais em magnitude e opostas em direção, de modo que elas também não produzem nenhuma força líquida no circuito. A figura\(\PageIndex{2}\) mostra vistas do loop a partir de cima. O torque é definido como\(\tau = rF\sin \theta \), onde\(F\) está a força,\(r\) é a distância do pivô em que a força é aplicada e\(\theta\) é o ângulo entre\(r\)\(F\) e. Como visto na Figura\(\PageIndex{1a}\), a regra 1 da mão direita determina que as forças nos lados sejam iguais em magnitude e opostas em direção, de modo que a força líquida seja novamente zero. No entanto, cada força produz um torque no sentido horário. Uma vez que\(r = w/2\), o torque em cada segmento vertical é\(\left( w/2\right)F\sin\theta\), e os dois são adicionados para dar um torque total

    \[\tau = \frac{w}{2}F\sin\theta + \frac{2}{2}F\sin\theta = wF\sin\theta \label{22.9.1}\]

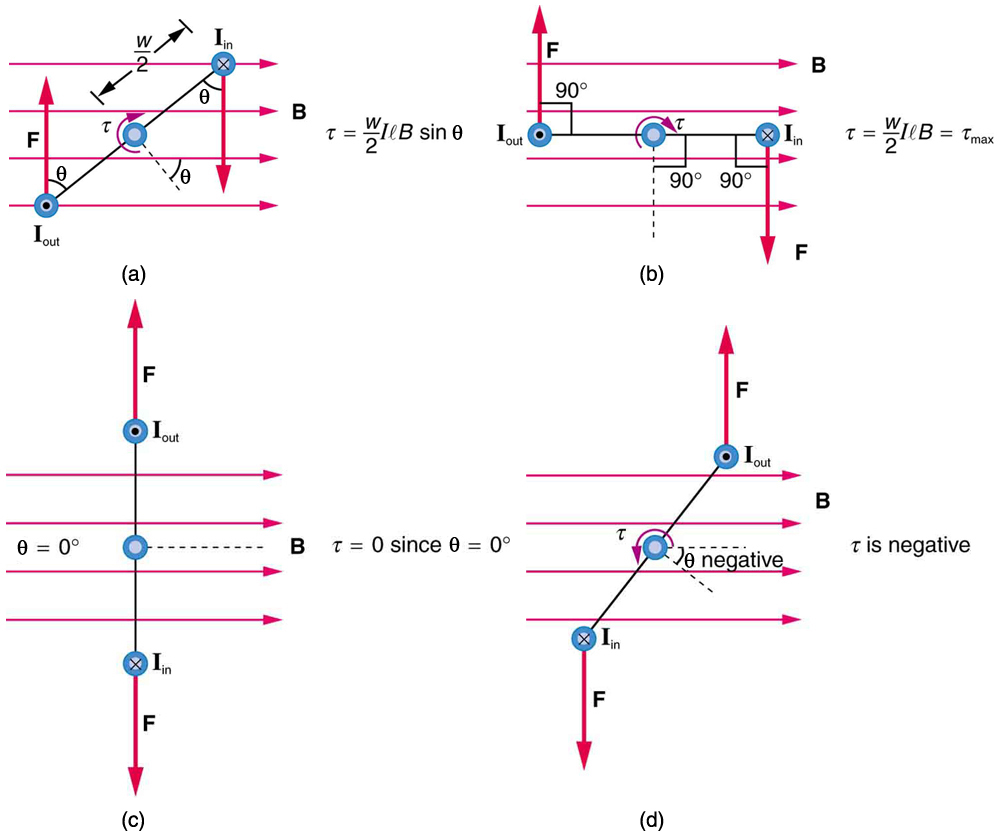
    Diagrama mostrando um circuito de transporte de corrente a partir do topo e quatro vezes diferentes enquanto ele gira em um campo magnético. O campo magnético orientado para a direita, perpendicular à dimensão vertical do circuito. Na figura a, a vista superior do circuito é orientada em um ângulo com as linhas do campo magnético, que vão da esquerda para a direita. A força no laço aumenta no lado inferior esquerdo, de onde a corrente sai da página. A força está baixa no lado superior direito, onde o laço entra na página. O ângulo entre a força e o laço é teta. O torque é no sentido horário e é igual a w mais de 2 vezes I l B seno teta. A Figura b mostra a vista superior do circuito paralela às linhas do campo magnético. A força no laço está no lado esquerdo, de onde eu saio da página. A força no laço está no lado direito, onde eu entro na página. O ângulo teta entre F e B é de noventa graus. O torque é no sentido horário e é igual a w acima de 2 I l B é igual ao torque máximo. A Figura c mostra a vista superior do loop orientada perpendicularmente a B. A força no loop está para cima na parte superior, de onde eu saio da página, e para baixo na parte inferior, onde entro na página. Theta é igual a 0 graus. O torque é igual a zero, já que o seno teta é igual a 0. Na figura d, a força está no lado inferior esquerdo do laço, onde eu entro, e no lado superior direito do laço, onde eu saio. O torque é no sentido anti-horário. O torque é negativo.
    Figura\(\PageIndex{2}\): Vistas superiores de um circuito transportador de corrente em um campo magnético. (a) A equação do torque é derivada usando essa visão. Observe que a perpendicular ao loop forma um ângulo\(\theta\) com o campo que é igual ao ângulo entre\(w/2\)\(F\) e. (b) O torque máximo ocorre quando\(\theta\) é um ângulo reto\(\sin \theta = 1\) e. (c) O torque zero (mínimo) ocorre quando\(\theta\) é zero\(\sin \theta = 0\) e. (d) O torque se inverte quando o circuito passa\(\theta = 0\).

    Agora, cada segmento vertical tem um comprimento\(l\) perpendicular a\(B\), de modo que a força em cada um é\(F = \pi B\). \(F\)Entrando na expressão de rendimentos de torque

    \[\tau = w \pi B \sin \theta.\label{22.9.2}\]

    Se tivermos um loop múltiplo de\(N\) voltas, obtemos o\(N\) dobro do torque de um loop. Finalmente, observe que a área do circuito é\(A = wl\); a expressão para o torque se torna

    \[\tau = NIAB \sin \theta.\label{22.9.3}\]

    Esse é o torque em um circuito de transporte de corrente em um campo magnético uniforme. Essa equação pode ser mostrada como válida para um loop de qualquer formato. O loop carrega uma corrente\(I\), tem\(N\) curvas, cada uma de área\(A\), e a perpendicular ao laço forma um ângulo\(\theta\) com o campo\(B\). A força líquida no circuito é zero.

    Exemplo\(\PageIndex{1}\): Calculating Torque on a Current-Carrying Loop in a Strong Magnetic Field

    Encontre o torque máximo em um circuito quadrado de 100 voltas de um fio de 10,0 cm em um lado que carrega 15,0 A de corrente em um campo de 2,00 T.

    Estratégia

    O torque no circuito pode ser encontrado usando\(\tau = NIAB\sin\theta\). O torque máximo ocorre quando\(\theta = 90^{\circ}\)\(\sin \theta = 1\) e.

    Solução

    Pois\(\sin \theta = 1\), o torque máximo é

    \[\tau_{max} = NIAB.\nonumber\]

    A inserção de valores conhecidos gera

    \[ \begin{align*} \tau_{max} &= \left(100\right)\left(15.0 A\right)\left(0.100 m^{2}\left)\right(2.00 T\right) \\[5pt] &= 30.0 N \cdot m. \end{align*}\]

    Discussão

    Esse torque é grande o suficiente para ser útil em um motor.

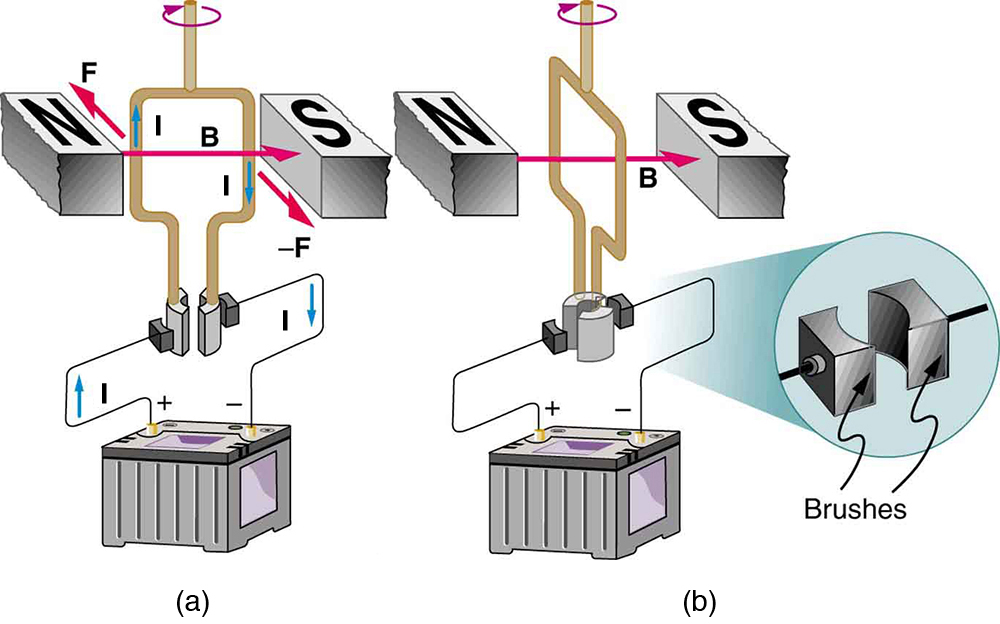
    O torque encontrado no exemplo anterior é o máximo. Conforme a bobina gira, o torque diminui para zero em\(\theta = 0\). O torque então inverte sua direção quando a bobina gira\(\theta = 0\) (Figura\(\PageIndex{1d}\)). Isso significa que, a menos que façamos algo, a bobina oscilará para frente e para trás em torno do equilíbrio em\(\theta = 0\). Isso significa que, a menos que façamos algo, a bobina oscilará para frente e para trás em torno do equilíbrio\(\theta = 0\) com interruptores automáticos chamados escovas (Figura\(\PageIndex{3}\)).

    O diagrama mostra um circuito de transporte de corrente entre os pólos norte e sul de um ímã em dois momentos diferentes. O pólo norte está à esquerda e o pólo sul está à direita. O campo magnético vai do pólo norte para a direita até o pólo sul. A Figura a mostra a corrente passando pelo loop. Ele corre para cima no lado esquerdo e para baixo no lado direito. A força no lado esquerdo está na página. A força no lado direito está fora da página. O torque é no sentido horário quando visto de cima. A Figura b mostra o laço quando ele é orientado perpendicularmente ao ímã. Em ambos os diagramas, a parte inferior de cada lado do circuito é conectada a um meio cilindro próximo a uma escova retangular que é então conectada ao resto do circuito.
    Figura\(\PageIndex{3}\): (a) À medida que o momento angular da bobina a transporta\(\theta = 0\), as escovas invertem a corrente para manter o torque no sentido horário. (b) A bobina girará continuamente no sentido horário, com a corrente invertendo a cada meia rotação para manter o torque no sentido horário.

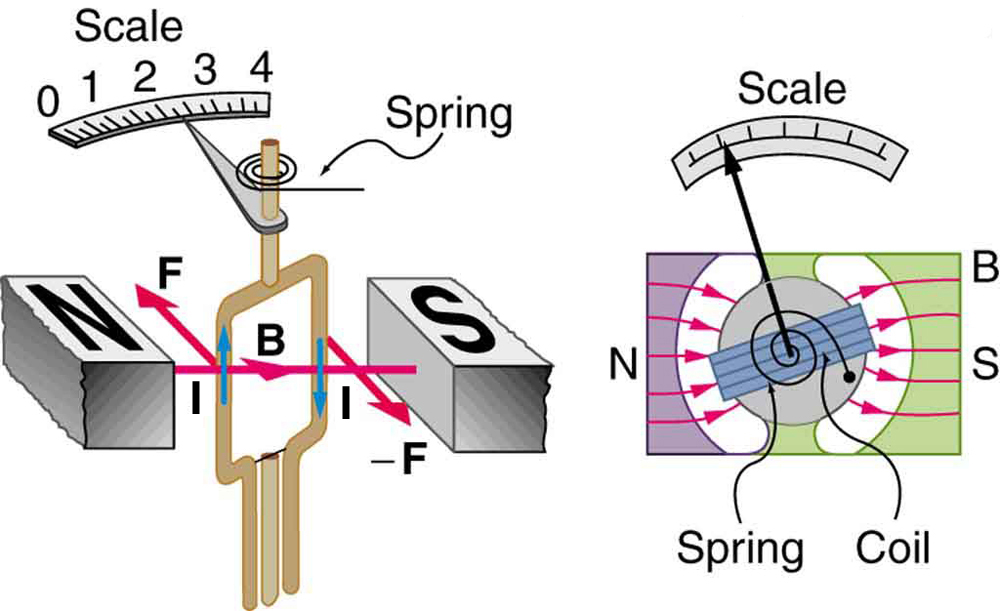
    Medidores, como os dos medidores de combustível analógicos de um carro, são outra aplicação comum de torque magnético em um circuito de transporte de corrente. A figura\(\PageIndex{4}\) mostra que um medidor é muito semelhante em construção a um motor. O medidor na figura tem seus ímãs moldados para limitar o efeito\(\theta\) de torná-los\(B\) perpendiculares ao laço em uma grande faixa angular. Assim, o torque é proporcional\(I\) e não\(\theta\). Uma mola linear exerce um contra-torque que equilibra o torque produzido pela corrente. Isso torna a deflexão da agulha proporcional\(I\) a. Se uma proporcionalidade exata não puder ser alcançada, a leitura do medidor pode ser calibrada. Para produzir um galvanômetro para uso em voltímetros analógicos e amperímetros que têm baixa resistência e respondem a pequenas correntes, usamos uma grande área de circuito\(A\), alto campo\(B\) magnético e bobinas de baixa resistência.

    Diagrama de um medidor mostrando um circuito de transporte de corrente entre dois pólos de um ímã. O torque no ímã é no sentido horário. A parte superior do laço é conectada a uma mola e a um ponteiro que aponta para uma escala à medida que o laço gira.
    Figura\(\PageIndex{4}\): Os medidores são muito semelhantes aos motores, mas giram apenas em uma parte de uma revolução. Os pólos magnéticos deste medidor são moldados para manter constante o componente\(B\) perpendicular ao circuito, de forma que o torque não dependa\(\theta\) e a deflexão contra a mola de retorno seja proporcional apenas à corrente\(I\).

    Resumo

    • O torque\(\tau\) em um circuito transportador de corrente de qualquer formato em um campo magnético uniforme.\(N\) é\[\tau = NIAB\sin\theta, \nonumber\] onde está o número de voltas,\(I\)\(A\) é a corrente, é a área do circuito,\(B\) é a intensidade do campo magnético e\(\theta\) é o ângulo entre a perpendicular ao circuito e ao campo magnético.

    Glossário

    motor
    laço de fio em um campo magnético; quando a corrente passa pelas alças, o campo magnético exerce torque nas alças, que giram um eixo; a energia elétrica é convertida em trabalho mecânico no processo
    contador
    aplicação comum de torque magnético em um circuito de transporte de corrente que é muito semelhante em construção a um motor; por design, o torque é proporcional \(I\)e não, então a deflexão da agulha é proporcional à corrente