Skip to main content
Global

22.7: Força magnética em um condutor transportador de corrente

  1. Last updated
  2. Save as PDF
  • Page ID
    194579

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Descreva os efeitos de uma força magnética em um condutor transportador de corrente.
    • Calcule a força magnética em um condutor transportador de corrente.

    Como as cargas normalmente não podem escapar de um condutor, a força magnética sobre as cargas que se movem em um condutor é transmitida ao próprio condutor.

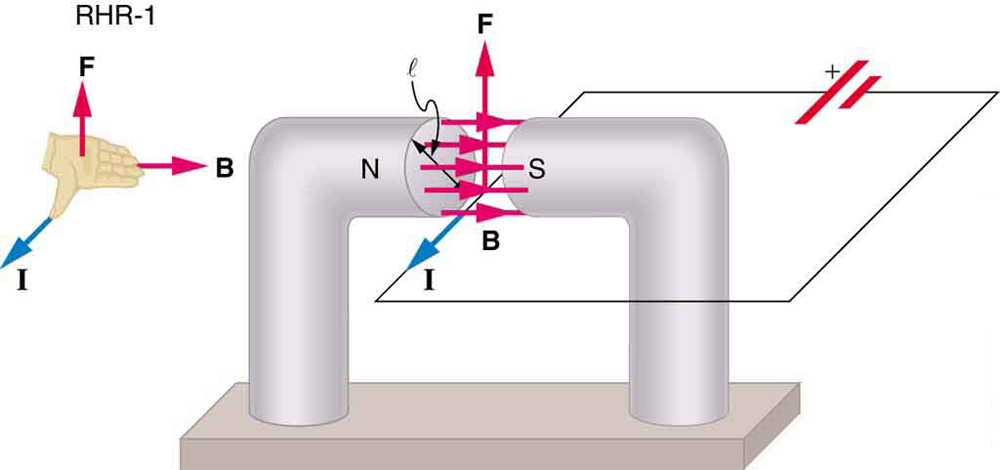
    Um diagrama mostrando um circuito com a corrente I passando por ele. Uma seção do fio passa entre os pólos norte e sul de um ímã com diâmetro l. O campo magnético B é orientado para a direita, do pólo norte ao sul do ímã, através do fio. A corrente sai da página. A força no fio é direcionada para cima. Uma ilustração da regra 1 da mão direita mostra o polegar apontando para fora da página na direção da corrente, os dedos apontando para a direita na direção de B e o vetor F apontando para cima e para longe da palma da mão.
    Figura\(\PageIndex{1}\): O campo magnético exerce uma força sobre um fio transportador de corrente em uma direção dada pela regra 1 da mão direita (a mesma direção das cargas móveis individuais). Essa força pode ser facilmente grande o suficiente para mover o fio, já que as correntes típicas consistem em um grande número de cargas móveis.

    Podemos derivar uma expressão para a força magnética em uma corrente tomando uma soma das forças magnéticas em cargas individuais. (As forças aumentam porque estão na mesma direção.) A força em uma carga individual que se move na velocidade de deriva\(v_{d}\) é dada por\(F = qv_{d}B\sin \theta \). Considerando\(B\) ser uniforme em um comprimento de fio\(l\) e zero em outro lugar, a força magnética total no fio é então\(F = \left(qv_{d}B \sin \theta \right) \left(N\right)\), onde\(N\) está o número de portadores de carga na seção do fio de comprimento\(l\). Agora\(N = nV\), onde\(n\) está o número de portadores de carga por unidade de volume e\(V\) é o volume de fio no campo. Observando que\(V = Al\), onde\(A\) está a área da seção transversal do fio, então está a força no fio\(F = \left(qv_{d}B\sin\theta\right))\left(nAl\right)\). Termos de coleta,

    \[F = \left(nqAv_{d}\right)lB\sin\theta . \label{22.8.1}\]

    Porque\(nqAv_{d} = I\) (veja Atual),

    \[F = \pi B \sin \theta \label{22.8.1b}\]

    é a equação da força magnética em um comprimento\(l\) de fio transportando uma corrente\(I\) em um campo magnético uniforme\(B\), conforme mostrado na Figura\(\PageIndex{2}\). Se dividirmos os dois lados dessa expressão por\(l\), descobrimos que a força magnética por unidade de comprimento do fio em um campo uniforme é\(\frac{}{} = IB \sin \theta \). A direção dessa força é dada pela RHR-1, com o polegar na direção da corrente\(I\). Então, com os dedos na direção de\(B\), uma perpendicular à palma aponta na direção de\(F\), como na Figura 2.

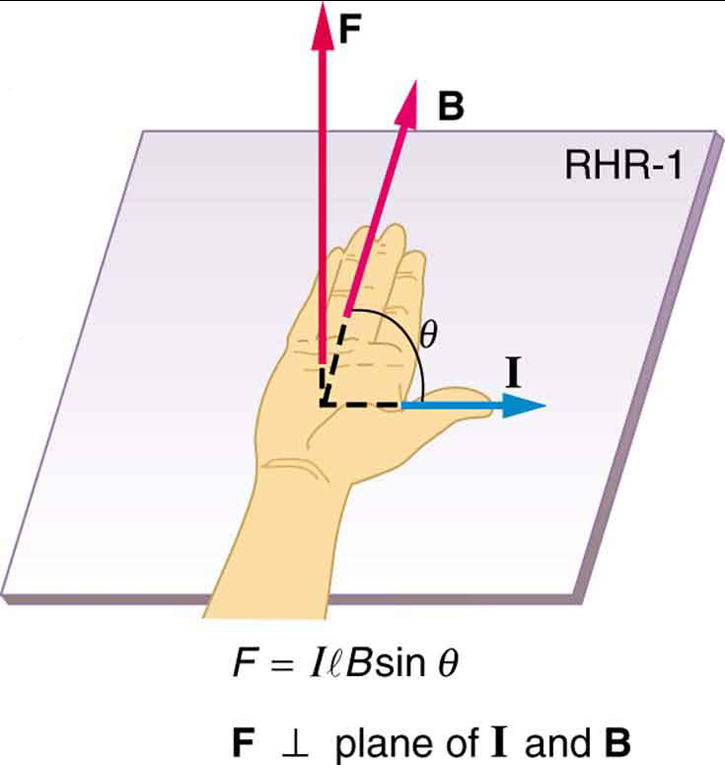
    Ilustração da regra 1 da mão direita mostrando o polegar apontando para a direita na direção da corrente I, os dedos apontando para a página com o campo magnético B e a força direcionada para cima, longe da palma da mão.
    Figura\(\PageIndex{2}\): A força em um fio transportador de corrente em um campo magnético é\(F = \pi B \sin \theta \). Sua direção é dada pela RHR-1.

    Exemplo\(\PageIndex{1}\): Calculating Magnetic Force on a Current-Carrying Wire: A Strong Magnetic Field

    Calcule a força no fio mostrado na Figura\(\PageIndex{1}\)\(B = 1.50 T\), dada\(l = 5.00 cm\),\(I = 20.0 A\) e.

    Estratégia

    A força pode ser encontrada com as informações fornecidas usando\(F = \pi B \sin\theta\) e observando que o ângulo\(\theta\) entre\(I\) e\(B\) é\(90^{\circ}\), de modo que\(sin \theta = 1\).

    Solução

    Inserindo os valores fornecidos em\(F = \pi B \sin \theta\) rendimentos

    \[F = \pi B \sin \theta = \left(20.0 A\right) \left(0.0500 m\right) \left(1.50 T\right) \left(1\right). \nonumber\]

    As unidades para tesla são\(1 T = \frac{N}{A \cdot m}\); portanto,

    \[F = 1.50 \,N. \nonumber\]

    Discussão

    Esse grande campo magnético cria uma força significativa em um pequeno comprimento de fio.

    A força magnética nos condutores transportadores de corrente é usada para converter energia elétrica em trabalho. (Os motores são um excelente exemplo: eles empregam laços de arame e são considerados na próxima seção.) Magnetohidrodinâmica (MHD) é o nome técnico dado a uma aplicação inteligente em que a força magnética bombeia fluidos sem mover partes mecânicas (Figura\(\PageIndex{3}\)).

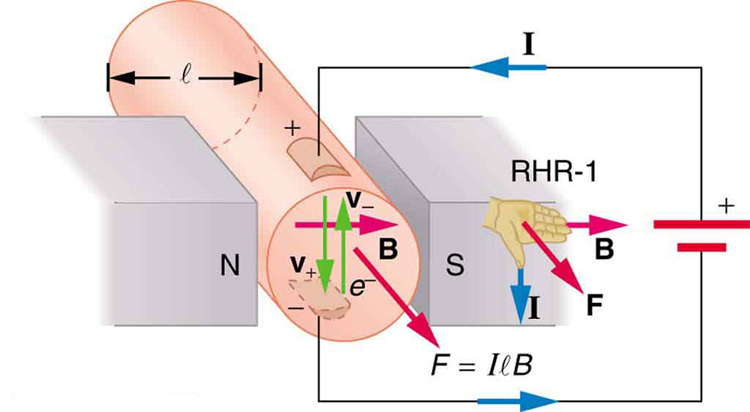
    Diagrama mostrando um cilindro de fluido de diâmetro l colocado entre os pólos norte e sul de um ímã. O pólo norte fica à esquerda. O pólo sul está à direita. O cilindro está orientado para fora da página. O campo magnético é orientado para a direita, do pólo norte para o sul e através do cilindro de fluido. Um fio transportador de corrente passa pelo cilindro de fluido com a corrente I orientada para baixo, perpendicular ao cilindro. Cargas negativas dentro do fluido têm um vetor de velocidade apontando para cima. Cargas positivas dentro do fluido têm um vetor de velocidade apontando para baixo. A força no fluido está fora da página. Uma ilustração da regra 1 da mão direita mostra o polegar apontando para baixo com a corrente, os dedos apontando para a direita com B e a força F orientada para fora da página, longe da palma da mão.
    Figura\(\PageIndex{3}\): Magnetohidrodinâmica. A força magnética na corrente passada por esse fluido pode ser usada como uma bomba não mecânica.

    Um forte campo magnético é aplicado em um tubo e uma corrente passa pelo fluido em ângulo reto com o campo, resultando em uma força no fluido paralela ao eixo do tubo, conforme mostrado. A ausência de partes móveis o torna atraente para mover uma substância quente e quimicamente ativa, como o sódio líquido empregado em alguns reatores nucleares. Corações artificiais experimentais estão testando com essa técnica o bombeamento de sangue, talvez evitando os efeitos adversos das bombas mecânicas. (As membranas celulares, no entanto, são afetadas pelos grandes campos necessários no MHD, atrasando sua aplicação prática em humanos.) A propulsão MHD para submarinos nucleares foi proposta, porque poderia ser consideravelmente mais silenciosa do que os acionamentos de hélice convencionais. O valor dissuasivo dos submarinos nucleares é baseado em sua capacidade de se esconder e sobreviver a um primeiro ou segundo ataque nuclear. À medida que lentamente desmontamos nossos arsenais de armas nucleares, o ramo submarino será o último a ser desativado por causa dessa habilidade (Figura\(\PageIndex{4}\)). Os drives MHD existentes são pesados e ineficientes — é necessário muito trabalho de desenvolvimento.

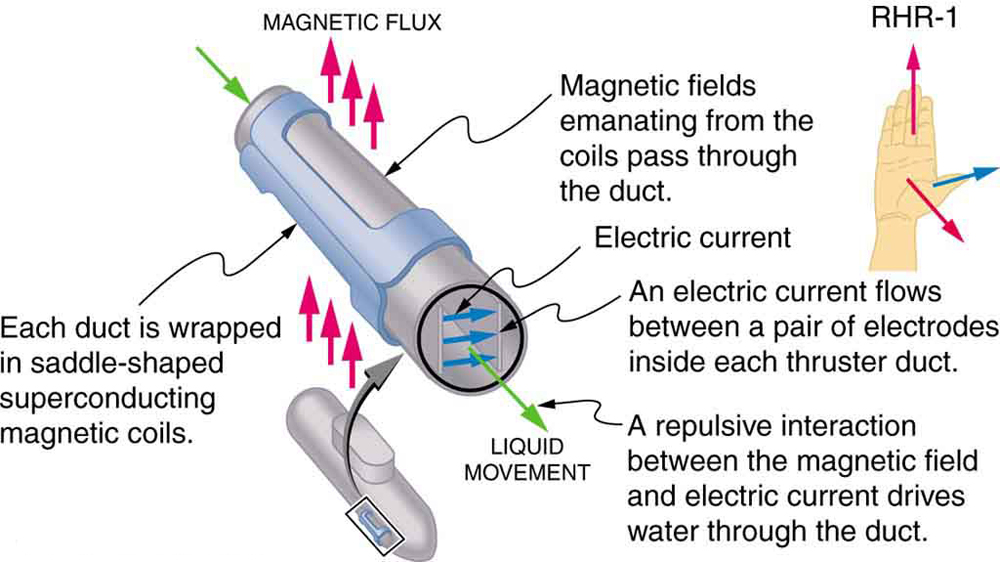
    Diagrama mostrando um zoom em um sistema de propulsão magnetohidrodinâmica em um submarino nuclear. O líquido se move através do duto do propulsor, que é orientado para fora da página. Os campos magnéticos emanam das bobinas e passam por um duto. O fluxo magnético é orientado para cima, perpendicular ao duto. Cada duto é enrolado em bobinas supercondutoras em forma de sela. Uma corrente elétrica corre para a direita, através do líquido e perpendicular à velocidade do líquido. A corrente elétrica flui entre um par de eletrodos dentro de cada duto do propulsor. Uma interação repulsiva entre o campo magnético e a corrente elétrica conduz a água através do duto. Uma ilustração da regra da mão direita mostra o polegar apontando para a direita com a corrente elétrica. Os dedos apontam para cima com o campo magnético. A força no líquido é orientada para fora da página, longe da palma da mão.
    Figura: Um sistema de propulsão\(\PageIndex{4}\) MHD em um submarino nuclear poderia produzir significativamente menos turbulência do que hélices e permitir que ele funcionasse de forma mais silenciosa. O desenvolvimento de um submarino com acionamento silencioso foi dramatizado no livro e no filme The Hunt for Red October.

    Resumo

    • A força magnética nos condutores portadores de corrente é dada por\[F = \pi B \sin \theta, \nonumber\] onde\(\) está a corrente,\(l\) é o comprimento de um condutor reto em um campo\(B\) magnético uniforme e\(\theta\) é o ângulo entre\(I\)\(B\) e. A força segue a RHR-1 com o polegar na direção de\(I\).