22.6: O efeito Hall

Last updated
Save as PDF

Page ID: 194550

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Descreva o efeito Hall.
Calcule o Hall emf em um condutor transportador de corrente.

Vimos os efeitos de um campo magnético em cargas em movimento livre. O campo magnético também afeta as cargas que se movem em um condutor. Um dos resultados é o efeito Hall, que tem implicações e aplicações importantes.

A figura\(\PageIndex{1}\) mostra o que acontece com as cargas que se movem através de um condutor em um campo magnético. O campo é perpendicular à velocidade de desvio do elétron e à largura do condutor. Observe que a corrente convencional está à direita em ambas as partes da figura. Na parte (a), os elétrons carregam a corrente e se movem para a esquerda. Na parte (b), cargas positivas carregam a corrente e se movem para a direita. Os elétrons em movimento sentem uma força magnética em direção a um lado do condutor, deixando uma carga positiva líquida do outro lado. Essa separação de carga cria uma tensão\(\varepsilon\), conhecida como Hall emf, através do condutor. a criação de uma tensão através de um condutor transportador de corrente por um campo magnético é conhecida como efeito Hall, em homenagem a Edwin Hall, o americano físico que o descobriu em 1879.

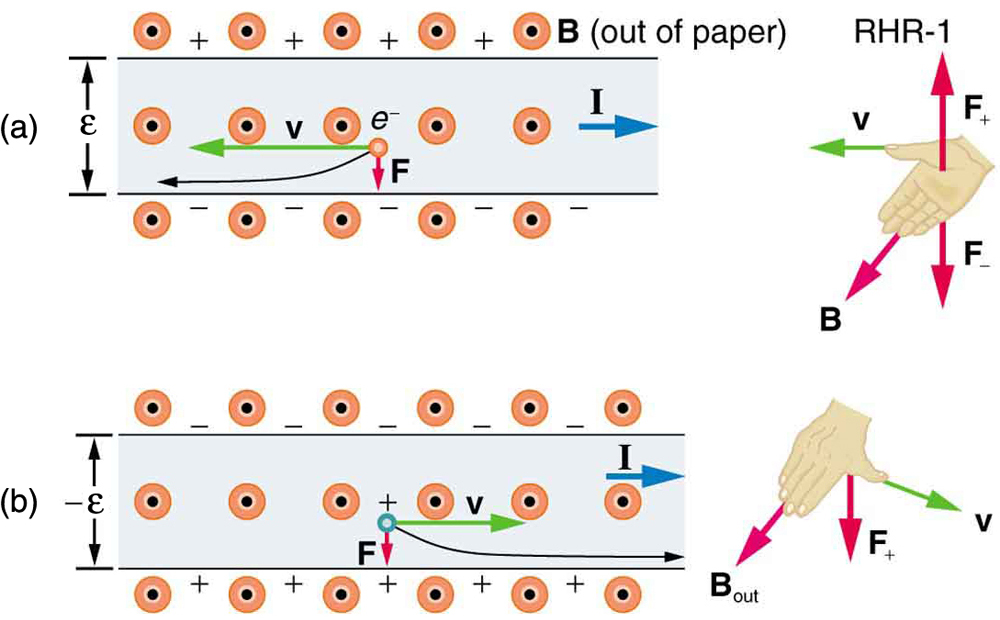
A figura a mostra um elétron com velocidade v se movendo para a esquerda. O campo magnético B está orientado para fora da página. A corrente I está correndo para a direita. O vetor de força no elétron aponta para baixo. Uma ilustração da regra da mão direita mostra o polegar direito apontando para a esquerda com o vetor v, os dedos apontando para as 7 horas com o vetor B, o vetor de força em uma carga positiva apontando para cima e o vetor de força em uma carga negativa apontando para baixo. A Figura b mostra uma carga positiva se movendo para a direita. As linhas do campo magnético estão saindo da página. A corrente I está correndo para a direita. A força na carga positiva está baixa. Uma ilustração da regra da mão direita mostra o polegar apontando na direção da velocidade da carga, os dedos apontando na direção de B e F apontando para baixo, longe da palma da mão. — Figura\(\PageIndex{1}\): O efeito Hall. (a) Os elétrons se movem para a esquerda neste condutor plano (corrente convencional para a direita). O campo magnético está diretamente fora da página, representado por pontos circulados; ele exerce uma força sobre as cargas em movimento, causando uma tensão\(\varepsilon\), a Hall emf, através do condutor. (b) Cargas positivas se movendo para a direita (corrente convencional também para a direita) são movidas para o lado, produzindo um Hall emf do sinal oposto,\(- \varepsilon\). Assim, se a direção do campo e a corrente forem conhecidas, o sinal dos portadores de carga pode ser determinado a partir do efeito Hall.

Um uso muito importante do efeito Hall é determinar se cargas positivas ou negativas carregam a corrente. Observe que na Figura 1b, onde cargas positivas carregam a corrente, o Hall emf tem o sinal oposto a quando cargas negativas carregam a corrente. Historicamente, o efeito Hall foi usado para mostrar que os elétrons transportam corrente em metais e também mostra que cargas positivas carregam corrente em alguns semicondutores. O efeito Hall é usado hoje como uma ferramenta de pesquisa para sondar o movimento de cargas, suas velocidades e densidades de deriva e assim por diante, em materiais. Em 1980, foi descoberto que o efeito Hall é quantizado, um exemplo de comportamento quântico em um objeto macroscópico.

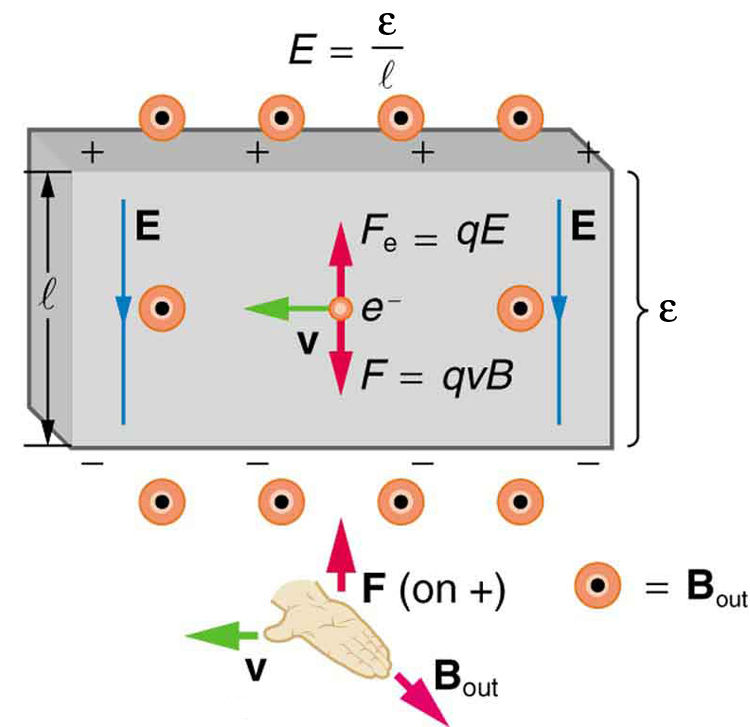
O efeito Hall tem outros usos que vão desde a determinação da taxa de fluxo sanguíneo até a medição precisa da intensidade do campo magnético. Para examiná-los quantitativamente, precisamos de uma expressão para o Hall emf,\(\varepsilon\), em um condutor. Considere o equilíbrio de forças em uma carga em movimento em uma situação em que\(B\)\(v\), e\(l\) são mutuamente perpendiculares, como mostrado na Figura\(\PageIndex{2}\). Embora a força magnética mova cargas negativas para um lado, elas não podem se acumular sem limite. O campo elétrico causado por sua separação se opõe à força magnética\(F = qvB\), e a força elétrica\(F_{e} = qE\), eventualmente cresce para se igualar a ela. Ou seja,

\[qE = qvB \nonumber\]

\[E = vB. \nonumber\]

Observe que o campo elétrico\(E\) é uniforme em todo o condutor porque o campo magnético\(B\) é uniforme, assim como o condutor. Para um campo elétrico uniforme, a relação entre campo elétrico e tensão é\(E = \varepsilon / l \), onde\(l\) está a largura do condutor e\(\varepsilon\) é o Hall emf. Ao inserir isso na última expressão, obtém-se:

\[\frac{\varepsilon}{l} = vB.\nonumber\]

Resolvendo isso para os rendimentos de Hall emf

\[\varepsilon = Blv \label{22.7.4}\]

se\(B\)\(v\), e\(l\) são mutuamente perpendiculares.

onde\(\varepsilon\) está a tensão do efeito Hall em um condutor de largura\(l\) através da qual as cargas se movem a uma velocidade\(v\).

Diagrama mostrando um elétron se movendo para a esquerda em um espaço retangular tridimensional com velocidade v. O campo magnético é orientado para fora da página. O campo elétrico está inativo. A força elétrica na carga aumenta enquanto a força magnética na carga está baixa. Uma ilustração da regra da mão direita mostra o polegar apontando para a esquerda com v, os dedos para fora da página com B e a força em uma carga positiva para cima e para longe da palma da mão. — Figura\(\PageIndex{2}\): O Hall emf\(\varepsilon\) produz uma força elétrica que equilibra a força magnética nas cargas em movimento. A força magnética produz separação de carga, que se acumula até ser balanceada pela força elétrica, um equilíbrio que é rapidamente alcançado.

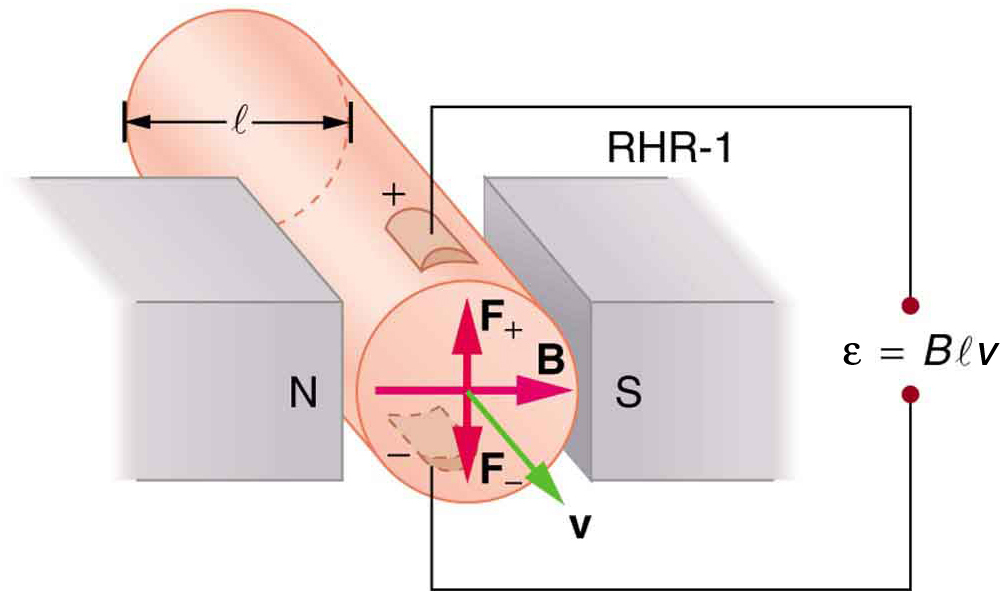
Um dos usos mais comuns do efeito Hall é na medição da intensidade do campo magnético\(B\). Esses dispositivos, chamados de sondas Hall, podem ser muito pequenos, permitindo um mapeamento preciso da posição. As sondas Hall também podem ser muito precisas, geralmente realizadas por meio de uma calibração cuidadosa. Outra aplicação do efeito Hall é medir o fluxo de fluido em qualquer fluido que tenha cargas livres (a maioria tem) (Figura\(\PageIndex{3}\)). Um campo magnético aplicado perpendicularmente à direção do fluxo produz um Hall emf\(\varepsilon\), conforme mostrado. Observe que o sinal de não\(\varepsilon\) depende do sinal das cobranças, mas apenas das direções de\(B\)\(v\) e. A magnitude do Hall emf é\(\varepsilon = Blv\), onde\(l\) está o diâmetro do tubo, de modo que a velocidade média\(v\) pode ser determinada\(\varepsilon\) desde que os outros fatores sejam conhecidos.

Diagrama mostrando um tubo com diâmetro l com uma extremidade entre os pólos norte e sul de um ímã. As cargas estão se movendo com a velocidade v dentro do tubo e para fora da página. O campo magnético B é orientado através do tubo, do pólo norte ao sul do ímã. A força nas cargas é maior para cargas positivas e baixa para cargas negativas. e m f = B l v. — Figura\(\PageIndex{3}\): O efeito Hall pode ser usado para medir o fluxo de fluido em qualquer fluido com cargas livres, como sangue. O Hall emf\(\varepsilon\) é medido através do tubo perpendicular ao campo magnético aplicado e é proporcional à velocidade média\(v\).

Exemplo\(\PageIndex{1}\): Calculating the Hall emf - Hall Effect for Blood Flow

Uma sonda de fluxo de efeito Hall é colocada em uma artéria, aplicando um campo magnético de 0,100 T sobre ela, em uma configuração semelhante à da Figura\(\PageIndex{3}\). O que é o Hall emf, dado que o diâmetro interno do vaso é de 4,00 mm e a velocidade média do sangue é de 20,0 cm/s?

Estratégia:

Como\(B\)\(v\), e\(l\) são mutuamente perpendiculares, a Equação\ ref {22.7.4} pode ser usada para encontrar\(\varepsilon\).

Solução:

Inserindo os valores fornecidos para\(B\)\(v\), e\(l\) dá

\[\begin{align*} \varepsilon &= Blv \\[4pt] &= \left(0.100 T\right) \left(4.00 \times 10^{-3} m\right) \left(0.200 m/s\right) \\[5pt] &= 80.0 \mu V \end{align*}\]

Discussão:

Essa é a saída de tensão média. A voltagem instantânea varia com o fluxo sanguíneo pulsante. A voltagem é pequena nesse tipo de medição. \(\varepsilon\)é particularmente difícil de medir, porque há voltagens associadas à ação cardíaca (voltagens de ECG) que são da ordem de milivolts. Na prática, essa dificuldade é superada aplicando um campo magnético AC, de forma que o Hall emf seja AC com a mesma frequência. Um amplificador pode ser muito seletivo ao escolher apenas a frequência apropriada, eliminando sinais e ruídos em outras frequências.

Resumo

O efeito Hall é a criação de tensão\(\varepsilon\), conhecida como Hall emf, através de um condutor transportador de corrente por um campo magnético.
O Hall emf é dado por\[\varepsilon = Blv\nonumber\] with\(B\),\(v\), e\(l\) todos mutuamente perpendiculares para um condutor de largura\(l\) através do qual as cargas se movem a uma velocidade\(v\).

Glossário

Efeito Hall: a criação de tensão através de um condutor transportador de corrente por um campo magnético

Hall emf: a força eletromotriz criada por um condutor transportador de corrente por um campo magnético,\(ε=Blv\)