21.6: Circuitos DC contendo resistores e capacitores
- Page ID
- 194059
Objetivos de
Ao final desta seção, você poderá:
- Explique a importância da constante de tempo, ω, e calcule a constante de tempo para uma determinada resistência e capacitância.
- Explique por que as baterias de uma lanterna gradualmente perdem energia e a luz diminui com o tempo.
- Descreva o que acontece com um gráfico da voltagem em um capacitor ao longo do tempo enquanto ele carrega.
- Explique como um circuito de temporização funciona e liste algumas aplicações.
- Calcule a velocidade necessária de um flash estroboscópico necessário para “interromper” o movimento de um objeto em um determinado comprimento.
Quando você usa uma câmera com flash, leva alguns segundos para carregar o capacitor que alimenta o flash. O flash de luz descarrega o capacitor em uma pequena fração de segundo. Por que o carregamento demora mais do que o descarregamento? Essa questão e vários outros fenômenos que envolvem carregamento e descarregamento de capacitores são discutidos neste módulo.
Circuitos RC
Um\(RC\) circuito é aquele que contém um resistor r\(R\) e um capacitor\(C\). O capacitor é um componente elétrico que armazena carga elétrica.
A figura mostra um\(RC\) circuito simples que emprega uma fonte de tensão DC (corrente contínua). O capacitor está inicialmente descarregado. Assim que o interruptor é fechado, a corrente flui de e para o capacitor inicialmente descarregado. À medida que a carga aumenta nas placas do capacitor, há uma oposição crescente ao fluxo de carga pela repulsão de cargas semelhantes em cada placa.
Em termos de tensão, isso ocorre porque a tensão no capacitor é dada por\(V_c = Q/C\), onde\(Q\) está a quantidade de carga armazenada em cada placa e\(C\) é a capacitância. Essa voltagem se opõe à bateria, aumentando de zero para o máximo de emf quando totalmente carregada. A corrente, portanto, diminui de seu valor inicial de\(I_9 = \frac{emf}{R}\) para zero à medida que a tensão no capacitor atinge o mesmo valor que o emf. Quando não há corrente, não há\(IR\) queda e, portanto, a tensão no capacitor deve ser igual à emf da fonte de tensão. Isso também pode ser explicado com a segunda regra de Kirchhoff (a regra do loop), discutida nas Regras de Kirchhoff, que diz que a soma algébrica das mudanças no potencial em torno de qualquer circuito fechado deve ser zero.
A corrente inicial é\(I_0 = \frac{emf}{R}\), porque toda a\(IR\) queda está na resistência. Portanto, quanto menor a resistência, mais rápido um determinado capacitor será carregado. Observe que a resistência interna da fonte de tensão está incluída\(R\), assim como as resistências do capacitor e dos fios de conexão. No cenário da câmera com flash acima, quando as baterias que alimentam a câmera começam a se desgastar, sua resistência interna aumenta, reduzindo a corrente e aumentando o tempo necessário para se preparar para o próximo flash.
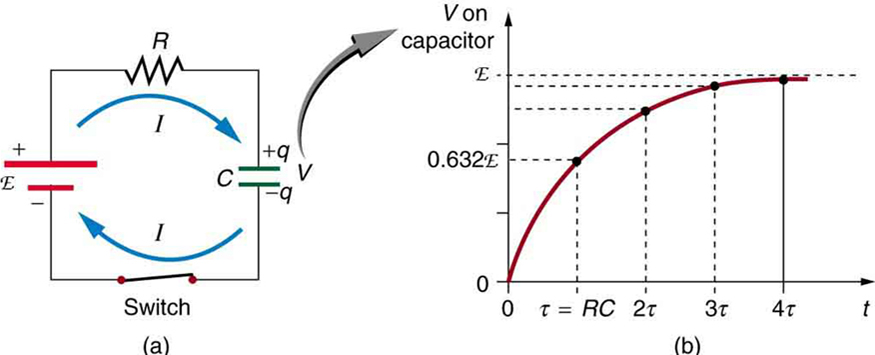
A tensão no capacitor é inicialmente zero e aumenta rapidamente no início, já que a corrente inicial é máxima. A Figura (b) mostra um gráfico da tensão do capacitor versus o tempo (\(t\)) começando quando o interruptor é fechado em\(t - 0\). A tensão se aproxima de emf de forma assintotica, pois quanto mais perto ela chega de emf, menos corrente flui. A equação para tensão versus tempo ao carregar um capacitor\(C\) através de um resistor\(R\), derivada usando cálculo,\(V\) é\[V = emf(1 - e^{-t/RC})(charging),\] onde está a tensão através do capacitor, emf é igual à emf da fonte de tensão DC e o exponencial e = 2,718... é a base do natural logaritmo. Observe que as unidades de\(RC\) são segundos. Definimos\[\tau = RC,\] onde\(\tau\) (a letra grega tau) é chamada de constante de tempo para um\(RC\) circuito. Conforme observado anteriormente, uma pequena resistência\(R\) permite que o capacitor carregue mais rápido. Isso é razoável, pois uma corrente maior flui por uma resistência menor. Também é razoável que quanto menor o capacitor\(C\), menos tempo necessário para carregá-lo. Ambos os fatores estão contidos em\(\tau = RC\).
Mais quantitativamente, considere o que acontece quando\(t = \tau = RC\). Então, a voltagem no capacitor é\[V = emf(1 - e^{-1}) = emf(1 - 0.368) = 0.632 \cdot emf.\]
Isso significa que, no momento\(\tau = RC\), a tensão sobe para 0,632 de seu valor final. A tensão aumentará 0,632 do restante na próxima vez.\(\tau\) É uma característica da função exponencial que o valor final nunca seja alcançado, mas 0,632 do restante desse valor é alcançado em todas as vezes\(\tau\). Em apenas alguns múltiplos da constante de tempo\(\tau\), então, o valor final é quase alcançado, como ilustra o gráfico na Figura (b).
Descarregando um capacitor
A descarga de um capacitor por meio de um resistor ocorre de maneira semelhante, como ilustra a Figura. Inicialmente, a corrente é\(I_9 - \frac{V_0}{R}\) acionada pela tensão inicial\(V_0\) no capacitor. Conforme a tensão diminui, a corrente e, portanto, a taxa de descarga diminuem, o que implica outra fórmula exponencial para\(V\). Usando o cálculo, a tensão\(V\) em um capacitor\(C\) que está sendo descarregado por meio de um resistor\(R\) é\[V = V_0 e^{-t/RC} (discharging).\]
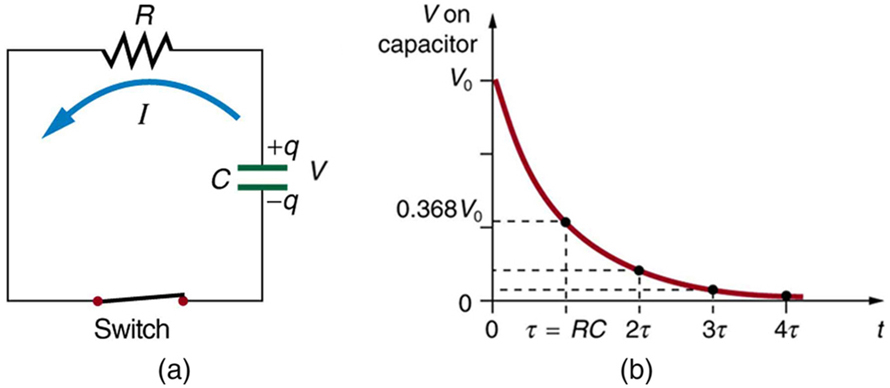
O gráfico na Figura (b) é um exemplo desse decaimento exponencial. Novamente, a constante de tempo é\(\tau = RC\). Uma pequena resistência\(R\) permite que o capacitor seja descarregado em pouco tempo, já que a corrente é maior. Da mesma forma, uma pequena capacitância requer menos tempo para ser descarregada, pois menos carga é armazenada. No primeiro intervalo de tempo\(\tau = RC\) após o fechamento do interruptor, a tensão cai para 0,368 de seu valor inicial, desde então\(V = V_0 \cdot e^{-1} = 0.368 V_0\).
Durante cada tempo sucessivo\(\tau\), a tensão cai para 0,368 de seu valor anterior. Em alguns múltiplos de\(\tau\), a tensão se torna muito próxima de zero, conforme indicado pelo gráfico na Figura (b).
Agora podemos explicar por que a câmera com flash em nosso cenário leva muito mais tempo para carregar do que para descarregar; a resistência durante o carregamento é significativamente maior do que durante a descarga. A resistência interna da bateria é responsável pela maior parte da resistência durante o carregamento. Conforme a bateria envelhece, o aumento da resistência interna torna o processo de carregamento ainda mais lento. (Você deve ter notado isso.)
A descarga instantânea ocorre através de um gás ionizado de baixa resistência no tubo de flash e ocorre muito rapidamente. Fotografias com flash, como na Figura, podem capturar um breve instante de um movimento rápido porque o flash pode ter menos de um microssegundo de duração. Esses flashes podem ser extremamente intensos.
Durante a Segunda Guerra Mundial, fotografias noturnas de reconhecimento foram feitas do ar com um único flash iluminando mais de um quilômetro quadrado do território inimigo. A brevidade do flash eliminou o embaçamento devido ao movimento da aeronave de vigilância. Hoje, um uso importante de lâmpadas de flash intensas é bombear energia para um laser. O flash curto e intenso pode energizar rapidamente um laser e permitir que ele reemita a energia em outra forma.

Exemplo\(\PageIndex{1}\) : Integrated Concept Problem: Calculating Capacitor Size—Strobe Lights
A fotografia com flash de alta velocidade foi pioneira por Doc Edgerton na década de 1930, enquanto ele era professor de engenharia elétrica no MIT. Você pode ter visto exemplos de seu trabalho nas fotos incríveis de beija-flores em movimento, uma gota de leite respingando em uma mesa ou uma bala penetrando em uma maçã (veja a Figura). Para interromper o movimento e capturar essas fotos, é necessário um flash pulsado de alta intensidade e muito curto, conforme mencionado anteriormente neste módulo.
Suponha que alguém deseje capturar a imagem de uma bala (movendo-se para\(5 \times 10^2 \, m/s\) cima) que estava passando por uma maçã. A duração do flash está relacionada à constante de\(RC\) tempo\(\tau\). Qual tamanho de capacitor seria necessário no\(RC\) circuito para ter sucesso, se a resistência do tubo de flash fosse\(10 \, \Omega\)? Suponha que a maçã seja uma esfera com um diâmetro de\(8 \times 10^{-2} \, m\).
Estratégia
Começamos identificando os princípios físicos envolvidos. Este exemplo trata da luz estroboscópica, conforme discutido acima. A figura mostra o circuito dessa sonda. O tempo característico\(\tau\) do estroboscópio é dado como\(\tau = RC\).
Solução
Queremos encontrar\(C\), mas não sabemos\(\tau\). Queremos que o flash fique aceso somente enquanto a bala atravessa a maçã. Então, precisamos usar as equações cinemáticas que descrevem a relação entre distância\(x\)\(v\), velocidade e tempo\(t\):
\[x = vt \, or \, t - \dfrac{x}{v}.\]
A velocidade da bala é dada como\(5 \times 10^2 \, m\), e a distância\(x\) é\(8 \times 10^{-2} \, m\). O tempo de travessia, então, é
\[t = \dfrac{x}{v} = \dfrac{8.0 \times 10^{-2} \, m}{5.0 \times 10^2 \, m/s} = 1.6 \times 10^{-4} \, s.\]
Definimos esse valor para o tempo de travessia\(t\) igual\(\tau\) a. Portanto,
\[C = \dfrac{t}{R} = \dfrac{1.6 \times 10^{-4} \, s}{10.0 \, \Omega} = 16 \, \mu F.\]
(Nota: A capacitância\(C\) é normalmente medida em farads,\(F\), definida como Coulombs por volt. A partir da equação, vemos que isso também\(C\) pode ser declarado em unidades de segundos por ohm.)
Discussão
O intervalo de flash de\(160 \mu s\) (o tempo de rotação da bala) é relativamente fácil de obter hoje. As luzes estroboscópicas abriram novos mundos, da ciência ao entretenimento. As informações da foto da maçã e da bala foram usadas no Relatório da Comissão Warren sobre o assassinato do presidente John F. Kennedy em 1963 para confirmar que apenas uma bala foi disparada.
Circuitos RC para temporização
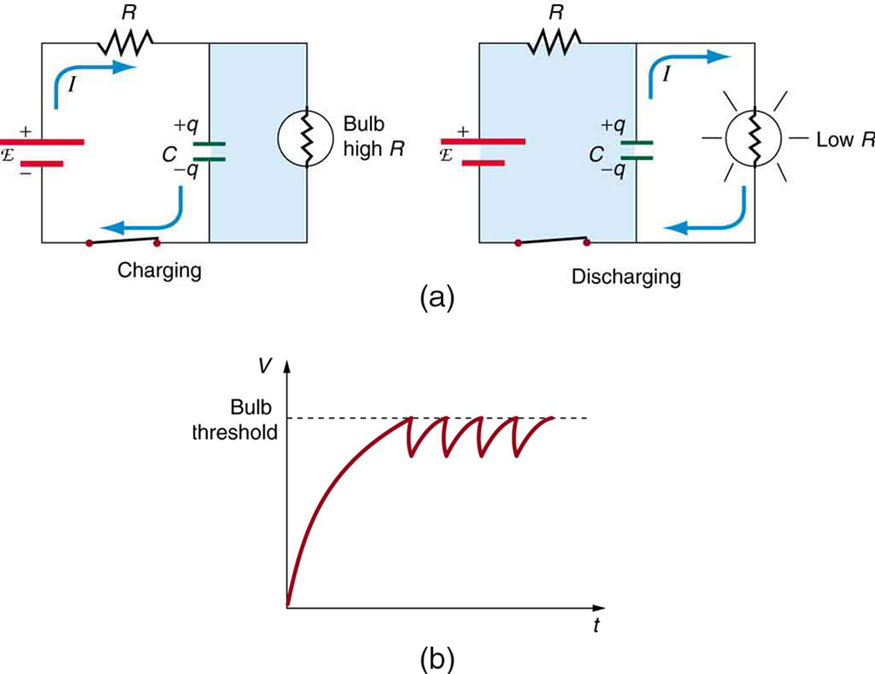
\(RC\)circuitos são comumente usados para fins de temporização. Um exemplo mundano disso é encontrado nos onipresentes sistemas de limpadores intermitentes dos carros modernos. O tempo entre os toalhetes varia de acordo com o ajuste da resistência em um\(RC\) circuito. Outro exemplo de\(RC\) circuito é encontrado em joias inovadoras, fantasias de Halloween e vários brinquedos com luzes intermitentes alimentadas por bateria. (Veja a Figura para ver um circuito de temporização.)
Um uso mais importante dos\(RC\) circuitos para fins de temporização é no marcapasso artificial, usado para controlar a frequência cardíaca. A frequência cardíaca normalmente é controlada por sinais elétricos gerados pelo nó sino-atrial (SA), que está na parede da câmara do átrio direito. Isso faz com que os músculos se contraiam e bombeiem sangue. Às vezes, o ritmo cardíaco é anormal e o batimento cardíaco está muito alto ou muito baixo.
O marcapasso artificial é inserido próximo ao coração para fornecer sinais elétricos ao coração quando necessário com a constante de tempo apropriada. Os marcapassos têm sensores que detectam o movimento corporal e a respiração para aumentar a frequência cardíaca durante o exercício e atender às maiores necessidades de sangue e oxigênio do corpo.
Exemplo \ (\ PageIndex {2}\): Calculando o tempo: circuito RC em um desfibrilador cardíaco
Um desfibrilador cardíaco é usado para ressuscitar uma vítima de acidente, descarregando um capacitor pelo tronco de seu corpo. Uma versão simplificada do circuito é vista na Figura. (a) Qual é a constante de tempo se um\(8.00 \, \mu F\) capacitor é usado e a resistência do caminho através de seu corpo é\(1 \times 10^3 \, \Omega\)? (b) Se a tensão inicial for de 10,0 kV, quanto tempo leva para diminuir para\(5 \times 10^2 \, V\)?
Estratégia
Como a resistência e a capacitância são dadas, é fácil multiplicá-las para obter a constante de tempo solicitada na parte (a). Para encontrar o tempo para que a tensão diminua\(5 \times 10^2 \, V\), multiplicamos repetidamente a tensão inicial por 0,368 até que uma tensão menor ou igual\(5 \times 10^2 \, V\) seja obtida. Cada multiplicação corresponde a um tempo de\(\tau\) segundos.
Solução para (a)
A constante de tempo\(\tau\) é dada pela equação\(\tau = RC\). Inserir os valores fornecidos para resistência e capacitância (e lembrar que as unidades de um farad podem ser expressas como\(s/\Omega\)) fornece
\[\tau = RC = (1.00 \times 10^3 \, \Omega)(8.00 \, \mu F) = 8.00 \, ms.\]
Solução para (b)
Nos primeiros 8,00 ms, a tensão (10,0 kV) diminui para 0,368 de seu valor inicial. Isso é:
\[V = 0.368 V_0 = 3.680 \times 10^3 \, V \, at \, t = 8.00 \, ms.\]
(Observe que carregamos um dígito extra para cada cálculo intermediário.) Depois de mais 8,00 ms, multiplicamos por 0,368 novamente e a tensão é
\[V' = 0.368 \, V\]
\[= (0.368)(3.680 \times 10^3 \, V)\]
\[=1.354 \times 10^3 \, V \, at \, t = 16.0 \, ms.\]
Da mesma forma, após mais 8,00 ms, a tensão é
\[V" = 0.368 \, V' = (0.368)(1.354 \times 10^3 \, V)\]
\[= 498 \, V \, at \, t = 24.0 \, ms.\]
Discussão
Então, após apenas 24,0 ms, a voltagem cai para 498 V, ou 4,98% de seu valor original. Esses breves tempos são úteis na desfibrilação cardíaca, porque a corrente breve, mas intensa, causa uma contração breve, mas eficaz, do coração. O circuito real em um desfibrilador cardíaco é um pouco mais complexo do que o da Figura, para compensar os efeitos magnéticos e de corrente alternada que serão cobertos pelo magnetismo.
Exercício\(\PageIndex{1}\)
Quando a diferença de potencial entre um capacitor é um emf?
- Resposta
-
Somente quando a corrente retirada ou colocada no capacitor é zero. Os capacitores, como as baterias, têm resistência interna, portanto, sua tensão de saída não é um emf, a menos que a corrente seja zero. Isso é difícil de medir na prática, então nos referimos à tensão de um capacitor em vez de sua emf. Mas a fonte da diferença de potencial em um capacitor é fundamental e é um emf.
EXPLORAÇÕES PHET: KIT DE CONSTRUÇÃO DE CIRCUITOS (SOMENTE DC)
Um kit eletrônico no seu computador! Construa circuitos com resistores, lâmpadas, baterias e interruptores. Faça medições com o amperímetro e o voltímetro realistas. Veja o circuito como um diagrama esquemático ou mude para uma visão realista.

Resumo da seção
- Um\(RC\) circuito é aquele que tem um resistor e um capacitor.
- A constante de tempo\(\tau\) para um\(RC\) circuito é\(\tau = RC\).
- Quando um\(t=0)\) capacitor\((V_0=0\) at inicialmente descarregado em série com um resistor é carregado por uma fonte de tensão DC, a tensão aumenta, aproximando-se assintoticamente do emf da fonte de tensão; em função do tempo,
\[V=emf(1−e^{−t/RC})(charging).\] - Dentro do intervalo de cada constante de tempo\(τ\), a tensão aumenta em 0,632 do valor restante, aproximando-se da tensão final de forma assintotica.
- Se um capacitor com uma tensão inicial\(V_0\) for descarregado por meio de um resistor começando em\(t=0\), sua tensão diminuirá exponencialmente conforme dado por
\[V=V_0e^{−t/RC}(discharging)\]. - Em cada constante de tempo, a tensão cai em 0,368 de seu valor inicial restante, aproximando-se de zero de forma assintotica.
Glossário
- Circuito RC
- um circuito que contém um resistor e um capacitor
- capacitor
- um componente elétrico usado para armazenar energia separando a carga elétrica em duas placas opostas
- capacitância
- a quantidade máxima de energia potencial elétrica que pode ser armazenada (ou separada) para um determinado potencial elétrico


