21.5: Medidas nulas

Last updated
Save as PDF

Page ID: 194049

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

objetivos de aprendizagem

Ao final desta seção, você poderá:

Explique por que um dispositivo de medição nulo é mais preciso do que um voltímetro ou amperímetro padrão.
Demonstre como uma ponte de Wheatstone pode ser usada para calcular com precisão a resistência em um circuito.

As medições padrão de tensão e corrente alteram o circuito que está sendo medido, introduzindo incertezas nas medições. Os voltímetros consomem alguma corrente extra, enquanto os amperímetros reduzem o fluxo de corrente. As medições nulas equilibram as tensões para que não haja corrente fluindo pelo dispositivo de medição e, portanto, nenhuma alteração do circuito que está sendo medido.

As medições nulas geralmente são mais precisas, mas também são mais complexas do que o uso de voltímetros e amperímetros padrão, e ainda têm limites para sua precisão. Neste módulo, consideraremos alguns tipos específicos de medições nulas, porque elas são comuns e interessantes e iluminam ainda mais os princípios dos circuitos elétricos.

O potenciômetro

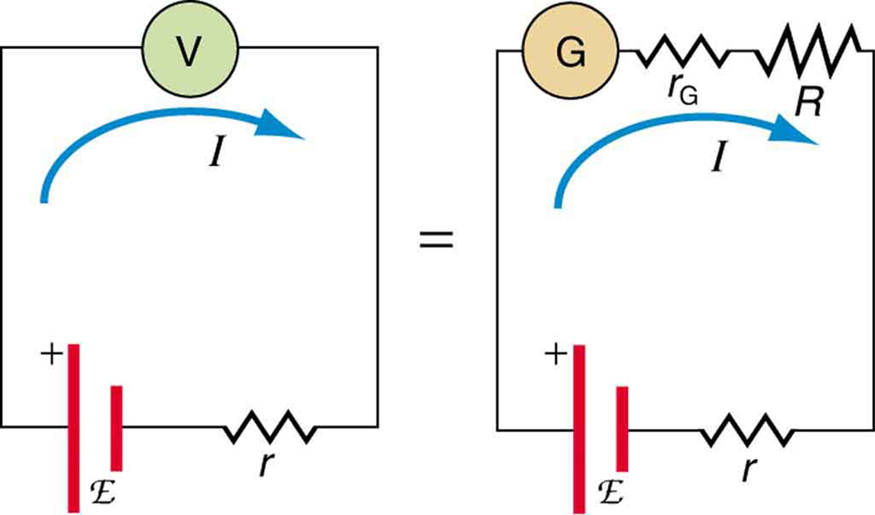
Suponha que você deseje medir o emf de uma bateria. Considere o que acontece se você conectar a bateria diretamente a um voltímetro padrão, conforme mostrado na Figura. (Depois de observarmos os problemas com essa medição, examinaremos uma medição nula que melhora a precisão.) Conforme discutido anteriormente, a quantidade real medida é a tensão do terminal\(V\), que está relacionada ao emf da bateria por\(V = emf - Ir\), onde\(I\) está a corrente que flui e\(r\) é a resistência interna da bateria.

O emf poderia ser calculado com precisão se\(r\) fosse conhecido com muita precisão, mas geralmente não é. Se a corrente\(I\) pudesse ser zero, então, e assim\(V = emf\), o emf poderia ser medido diretamente. No entanto, os voltímetros padrão precisam de uma corrente para operar; portanto, outra técnica é necessária.

O diagrama mostra a equivalência entre dois circuitos. O primeiro circuito tem uma célula de e m f script E e uma resistência interna r conectada através de um voltímetro. O circuito equivalente à direita mostra a mesma célula de e m f script E e uma resistência interna r conectada através de uma combinação em série de um galvanômetro com uma resistência interna r sub G e alta resistência R. As correntes nos dois circuitos são mostradas iguais. — Figura\(\PageIndex{1}\): Um voltímetro analógico conectado a uma bateria consome uma corrente pequena, mas diferente de zero, e mede uma tensão terminal que difere da emf da bateria. (Observe que a letra maiúscula E simboliza força eletromotriz, ou emf.) Como a resistência interna da bateria não é conhecida com precisão, não é possível calcular o emf com precisão.

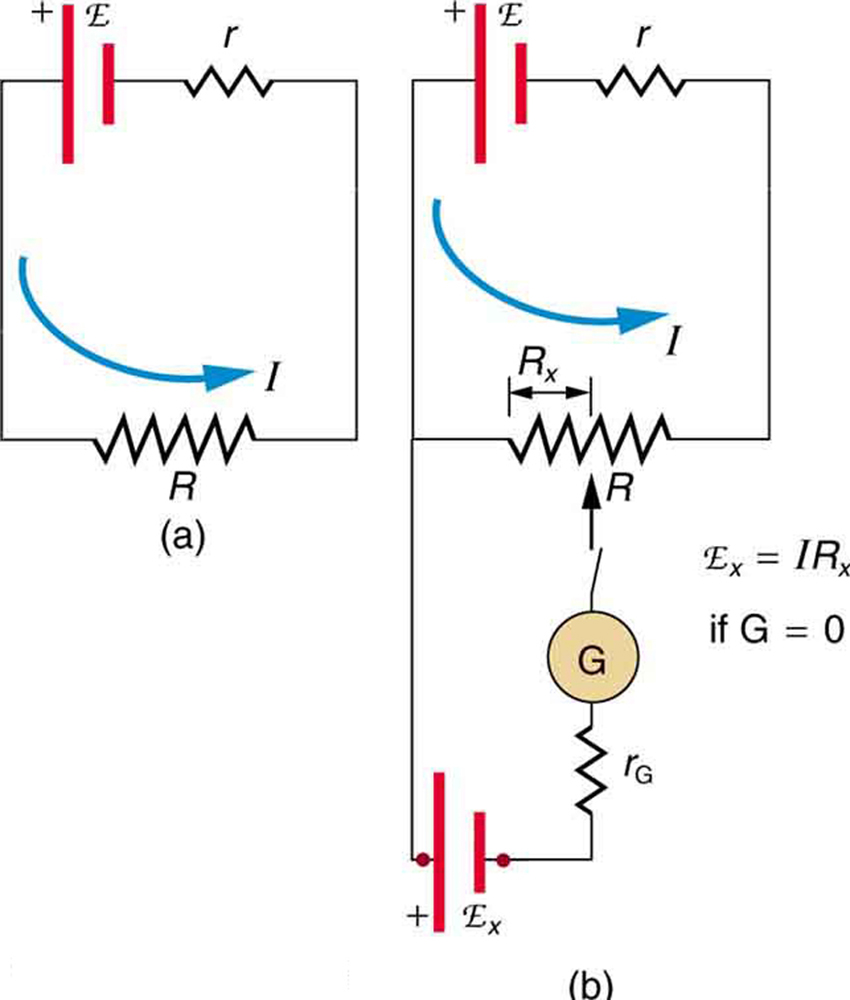
Um potenciômetro é um dispositivo de medição nulo para medir potenciais (voltagens). (Veja a Figura.) Uma fonte de tensão é conectada a um resistor,\(r\) digamos, um fio longo, e passa uma corrente constante através dele. Há uma queda constante no potencial (uma\(IR\) queda) ao longo do fio, de modo que um potencial variável pode ser obtido fazendo contato em locais variados ao longo do fio.

A Figura (b) mostra uma incógnita\(emf_x\) (representada pelo script\(E_x\) na figura) conectada em série com um galvanômetro. Note que\(emf_x\) se opõe à outra fonte de tensão. A localização do ponto de contato (veja a seta no desenho) é ajustada até o galvanômetro indicar zero. Quando o galvanômetro indica zero,\(emf_x = IR_x\) onde\(R_x\) está a resistência da seção do fio até o ponto de contato. Como nenhuma corrente flui pelo galvanômetro, nenhuma flui através do emf desconhecido e, portanto,\(emf_x\) é detectada diretamente.

Agora, um padrão conhecido com muita precisão\(emf_s\) é substituído e o ponto de contato é ajustado até que o galvanômetro novamente mostre zero, de modo que\(emf_s = IR_s\).\(emf_x\) Em ambos os casos, nenhuma corrente passa pelo galvanômetro e, portanto, a corrente\(I\) através do fio longo é a mesma. Ao tomar a proporção\(\frac{emf_x}{emf_s}\),\(I\) cancela, dando\[\dfrac{emf_x}{emf_s} = \dfrac{IR_x}{IR_s} = \dfrac{R_x}{R_s}.\]

Resolvendo\(emf_x\) doações\[emf_x = emf_s \dfrac{R_x}{R_s}.\]

Dois circuitos são mostrados. O primeiro circuito tem uma célula de e m f script E e resistência interna r conectada em série a um resistor R. O segundo diagrama mostra o mesmo circuito com a adição de um galvanômetro e uma fonte de tensão desconhecida conectada a um contato variável que pode ser ajustado para cima e para baixo no comprimento do resistor R. — Figura: O\(\PageIndex{2}\) potenciômetro, um dispositivo de medição nulo. (a) Uma fonte de tensão conectada a um resistor de fio longo passa uma corrente constante\(I\) através dele. (b) Um emf desconhecido (rotulado\(E_x\) na figura) é conectado conforme mostrado, e o ponto de contato\(R\) é ajustado até que o galvanômetro chegue a zero. O segmento do fio tem uma resistência\(R_x\) e um script\(E_x = IR_x\), onde não\(I\) é afetado pela conexão, pois nenhuma corrente flui pelo galvanômetro. O emf desconhecido é, portanto, proporcional à resistência do segmento do fio.

Como um fio longo e uniforme é usado para\(R\), a proporção de resistências\(R_x/R_s\) é a mesma que a proporção dos comprimentos do fio que zeram o galvanômetro para cada emf. As três quantidades no lado direito da equação agora são conhecidas ou medidas e\(emf_x\) podem ser calculadas. A incerteza nesse cálculo pode ser consideravelmente menor do que quando se usa um voltímetro diretamente, mas não é zero. Sempre há alguma incerteza na proporção de resistências\(R_x/R_s\) e no padrão\(emf_s\). Além disso, não é possível dizer quando o galvanômetro lê exatamente zero, o que introduz erro em ambos\(R_x\) e\(R_s\) também pode afetar a corrente\(I\).

Medições de resistência e a ponte de Wheatstone

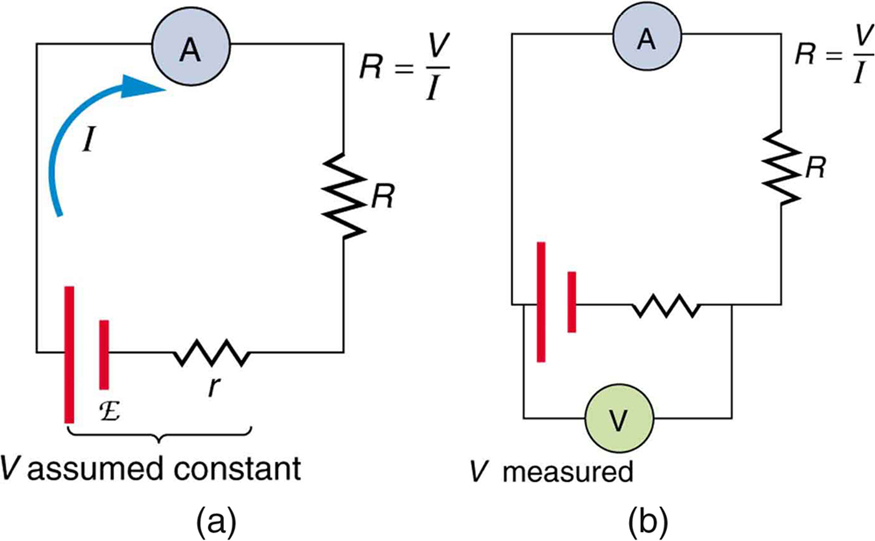
Há uma variedade dos chamados ohmímetros que pretendem medir a resistência. O que os ohmímetros mais comuns realmente fazem é aplicar uma tensão a uma resistência, medir a corrente e calcular a resistência usando a lei de Ohm. A leitura deles é essa resistência calculada. Duas configurações para ohmímetros usando voltímetros e amperímetros padrão são mostradas na Figura. Essas configurações são limitadas em precisão, porque os medidores alteram tanto a tensão aplicada ao resistor quanto a corrente que flui através dele.

O diagrama mostra dois circuitos. O primeiro tem uma célula de e m f script E e resistência interna r conectada em série a um amperímetro A e um resistor R. O segundo circuito é o mesmo que o primeiro, mas, além disso, há um voltímetro conectado através da fonte de tensão E. — Figura\(\PageIndex{3}\): Dois métodos para medir a resistência com medidores padrão. (a) Supondo uma tensão conhecida para a fonte, um amperímetro mede a corrente e a resistência é calculada como\(R = \frac{V}{I}\). (b) Como a tensão do terminal\(V\) varia com a corrente, é melhor medi-la. \(V\)é mais precisamente conhecido quando\(I\) é pequeno, mas por\(I\) si só é conhecido com mais precisão quando é grande.

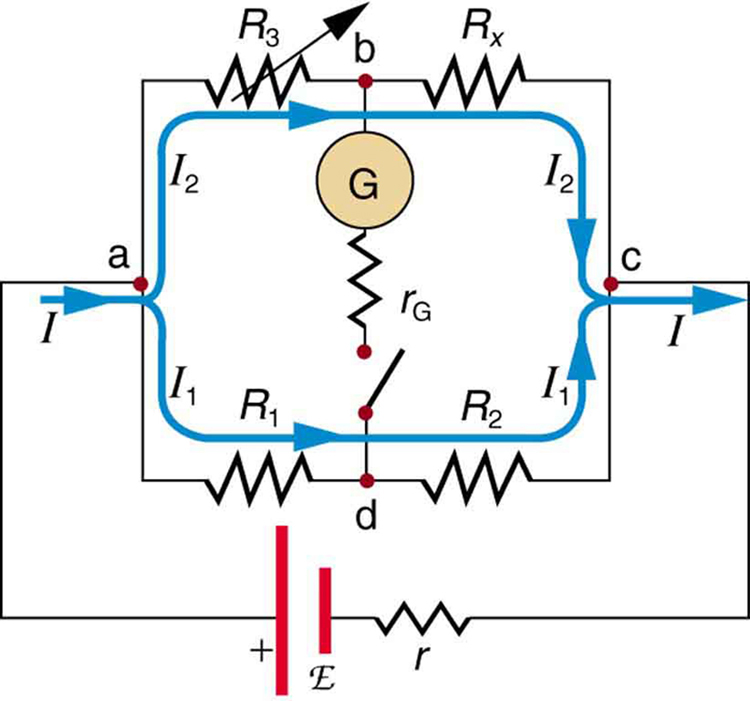
A ponte Wheatstone é um dispositivo de medição nulo para calcular a resistência ao equilibrar possíveis quedas em um circuito. (Veja a Figura.) O dispositivo é chamado de ponte porque o galvanômetro forma uma ponte entre dois ramos. Uma variedade de dispositivos de ponte é usada para fazer medições nulas em circuitos.

Resistores\(R_1\) e\(R_2\) são conhecidos com precisão, enquanto a seta\(R_3\) indica que é uma resistência variável. O valor de\(R_3\) pode ser lido com precisão. Com a resistência desconhecida\(R_x\) no circuito,\(R_3\) é ajustado até o galvanômetro indicar zero. A diferença de potencial entre os pontos b e d é então zero, o que significa que b e d têm o mesmo potencial. Sem corrente passando pelo galvanômetro, ele não tem efeito no resto do circuito. Portanto, as ramificações abc e adc estão em paralelo e cada ramificação tem a voltagem total da fonte. Ou seja, as\(IR\) quedas ao longo de abc e adc são as mesmas. Como b e d têm o mesmo potencial, a\(IR\) queda ao longo de ad deve ser igual à\(IR\) queda ao longo de ab. Assim,\[I_1R_1 = I_2R_2.\]

Novamente, como b e d têm o mesmo potencial, a\(IR\) queda ao longo de dc deve ser igual à\(IR\) queda ao longo de bc. Assim,\[I_1R_2 = I_2R_x.\] considerando a proporção dessas duas últimas expressões,\[\dfrac{I_1R_1}{I_1R_2} = \dfrac{I_2R_3}{I_2R_x}.\] cancelando as correntes e resolvendo R _x rendimentos\[R_x = R_3\dfrac{R_2}{R_1}.\]

Este complexo diagrama de circuito mostra um galvanômetro conectado no braço central de um arranjo de ponte de Wheatstone. Todos os outros quatro braços têm um resistor. A ponte é conectada a uma célula de e m f script E e resistência interna r. — Figura\(\PageIndex{4}\): A ponte Wheatstone é usada para calcular resistências desconhecidas. A resistência variável\(R_3\) é ajustada até que o galvanômetro leia zero com o interruptor fechado. Isso simplifica o circuito,\(R_x\) permitindo que seja calculado com base nas\(IR\) quedas, conforme discutido no texto.

Essa equação é usada para calcular a resistência desconhecida quando a corrente através do galvanômetro é zero. Esse método pode ser muito preciso (geralmente com quatro dígitos significativos), mas é limitado por dois fatores. Primeiro, não é possível fazer com que a corrente através do galvanômetro seja exatamente zero. Em segundo lugar, sempre há incertezas em\(R_1\),\(R_2\) e\(R_3\), que contribuem para a incerteza em\(R_x\).

Exercício\(\PageIndex{1}\)

Identifique outros fatores que possam limitar a precisão das medições nulas. O uso de um dispositivo digital mais sensível do que um galvanômetro melhoraria a precisão das medições nulas?

Resposta: Um fator seria a resistência nos fios e conexões em uma medição nula. Eles são impossíveis de fazer zero e podem mudar com o tempo. Outro fator seriam as variações de temperatura na resistência, que podem ser reduzidas, mas não completamente eliminadas pela escolha do material. Dispositivos digitais sensíveis a correntes menores do que dispositivos analógicos melhoram a precisão das medições nulas porque permitem que você aproxime a corrente de zero.

Resumo

As técnicas de medição nula alcançam maior precisão ao equilibrar um circuito para que nenhuma corrente flua pelo dispositivo de medição.
Um desses dispositivos, para determinar a tensão, é um potenciômetro.
Outro dispositivo de medição nulo, para determinar a resistência, é a ponte de Wheatstone.
Outras quantidades físicas também podem ser medidas com técnicas de medição nulas.

Glossário

medições nulas: métodos de medir a corrente e a tensão com mais precisão, balanceando o circuito para que nenhuma corrente flua através do dispositivo de medição

potenciômetro: um dispositivo de medição nulo para medir potenciais (voltagens)

ohmímetro: um instrumento que aplica uma tensão a uma resistência, mede a corrente, calcula a resistência usando a lei de Ohm e fornece uma leitura dessa resistência calculada

dispositivo de ponte: um dispositivo que forma uma ponte entre dois ramos de um circuito; alguns dispositivos de ponte são usados para fazer medições nulas em circuitos

Ponte Wheatstone: um dispositivo de medição nulo para calcular a resistência balanceando possíveis quedas em um circuito