21.E: Circuitos e instrumentos de corrente contínua (exercício)
- Page ID
- 194057
Perguntas conceituais
21.1: Resistores em série e paralelos
1. Um interruptor tem uma resistência variável que é quase zero quando fechado e extremamente grande quando aberto, e é colocado em série com o dispositivo que controla. Explique o efeito que o interruptor na Figura tem na corrente quando aberto e quando fechado.
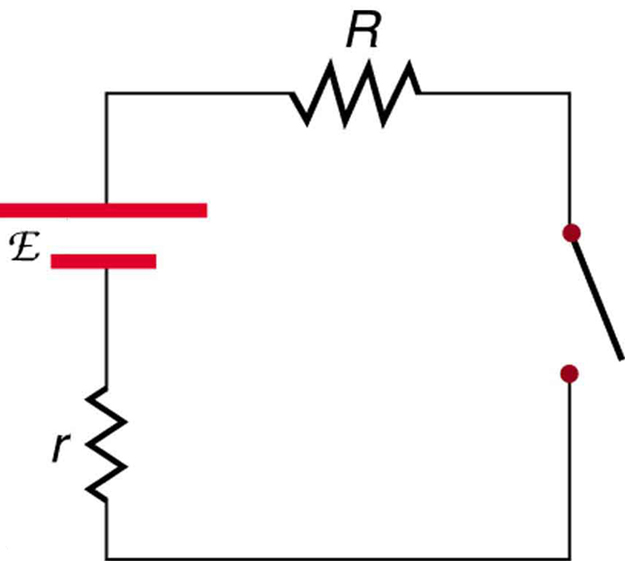
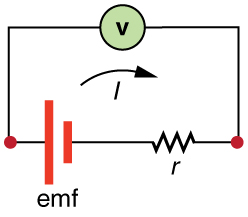
Normalmente, um interruptor está em série com uma fonte de resistência e tensão. Idealmente, o interruptor tem quase zero de resistência quando fechado, mas tem uma resistência extremamente grande quando aberto. (Observe que neste diagrama, o script E representa a tensão (ou força eletromotriz) da bateria.)
2. Qual é a voltagem no interruptor aberto na Figura?
3. Há uma voltagem em um interruptor aberto, como na Figura. Por que, então, a energia dissipada pelo interruptor aberto é pequena?
4. Por que a energia dissipada por um interruptor fechado, como na Figura, é pequena?
5. Um estudante em um laboratório de física conectou por engano uma lâmpada, bateria e interruptor, conforme mostrado na Figura. Explique por que a lâmpada está ligada quando o interruptor está aberto e desligada quando o interruptor está fechado. (Não tente fazer isso — é difícil para a bateria!)
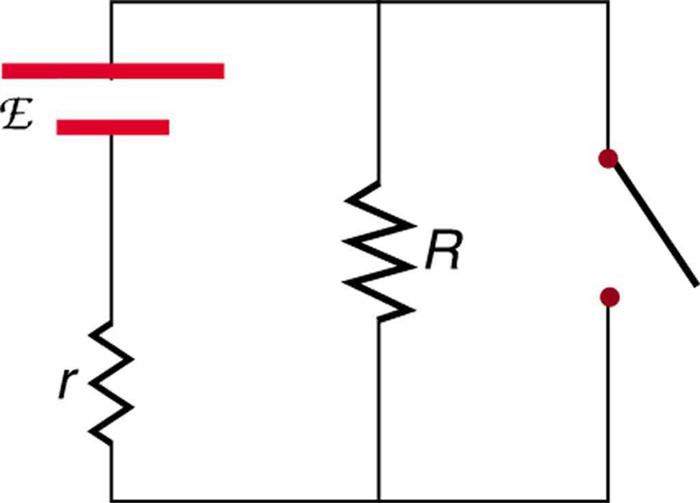
Um erro de fiação colocou esse interruptor em paralelo com o dispositivo representado por\(\displaystyle R\). (Observe que neste diagrama, o script E representa a tensão (ou força eletromotriz) da bateria.)
6. Sabendo que a gravidade de um choque depende da magnitude da corrente em seu corpo, você preferiria estar em série ou paralelo a uma resistência, como o elemento de aquecimento de uma torradeira, se chocado com ela? Explique.
7. Seus faróis diminuiriam quando você ligasse o motor do carro se os fios do automóvel fossem supercondutores? (Não negligencie a resistência interna da bateria.) Explique.
8. Algumas cadeias de luzes natalinas são conectadas em série para economizar custos de fiação. Uma versão antiga utilizava lâmpadas que interrompem a conexão elétrica, como um interruptor aberto, quando elas queimam. Se uma dessas lâmpadas se queimar, o que acontece com as outras? Se essa corda operar em 120 V e tiver 40 lâmpadas idênticas, qual é a tensão normal de operação de cada uma? As versões mais recentes usam lâmpadas que causam curto-circuito, como um interruptor fechado, quando elas queimam. Se uma dessas lâmpadas se queimar, o que acontece com as outras? Se essa corda operar em 120 V e tiver 39 lâmpadas idênticas restantes, qual é então a tensão de operação de cada uma?
9. Se duas lâmpadas domésticas de 60 W e 100 W estiverem conectadas em série à energia doméstica, qual será mais brilhante? Explique.
10. Suponha que você esteja fazendo um laboratório de física que solicite que você coloque um resistor em um circuito, mas todos os resistores fornecidos têm uma resistência maior do que o valor solicitado. Como você conectaria as resistências disponíveis para tentar obter o menor valor solicitado?
11. Antes da Segunda Guerra Mundial, alguns rádios eram alimentados por meio de um “cabo de resistência” que tinha uma resistência significativa. Esse cabo de resistência reduz a tensão até o nível desejado para os tubos do rádio e similares e economiza as despesas de um transformador. Explique por que os cabos de resistência ficam quentes e desperdiçam energia quando o rádio está ligado.
12. Algumas lâmpadas têm três configurações de energia (sem incluir zero), obtidas de vários filamentos que são comutados e conectados individualmente em paralelo. Qual é o número mínimo de filamentos necessários para três configurações de potência?
21.2: Força eletromotriz: tensão terminal
13. Cada emf é uma diferença potencial? Cada diferença de potencial é um emf? Explique.
14. Explique qual bateria está carregando e qual está sendo carregada na Figura.
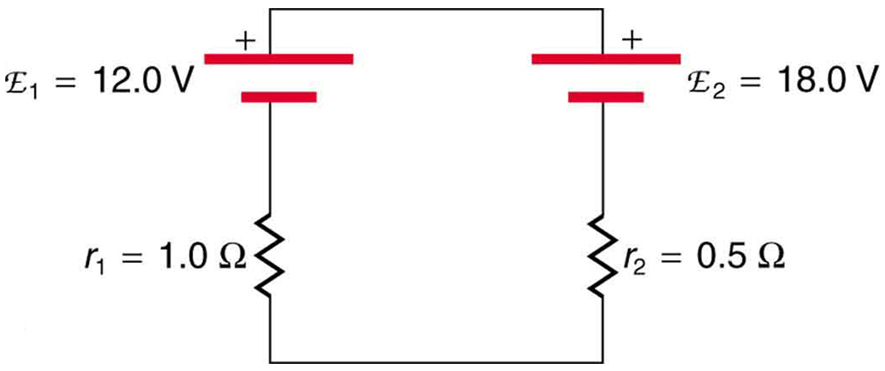
15. Com uma bateria, uma variedade de resistores e uma variedade de dispositivos de medição de tensão e corrente, descreva como você determinaria a resistência interna da bateria.
16. Duas baterias automotivas diferentes de 12 V em uma prateleira de loja são avaliadas em 600 e 850 “amplificadores de partida a frio”. Qual tem a menor resistência interna?
17. Quais são as vantagens e desvantagens de conectar baterias em série? Em paralelo?
18. Os caminhões semitratores usam quatro baterias grandes de 12 V. O sistema de partida requer 24 V, enquanto a operação normal dos outros componentes elétricos do caminhão utiliza 12 V. Como as quatro baterias podem ser conectadas para produzir 24 V? Para produzir 12 V? Por que 24 V é melhor do que 12 V para dar partida no motor do caminhão (uma carga muito pesada)?
21.3: Regras de Kirchhoff
19. Todas as correntes que entram na junção na Figura podem ser positivas? Explique.
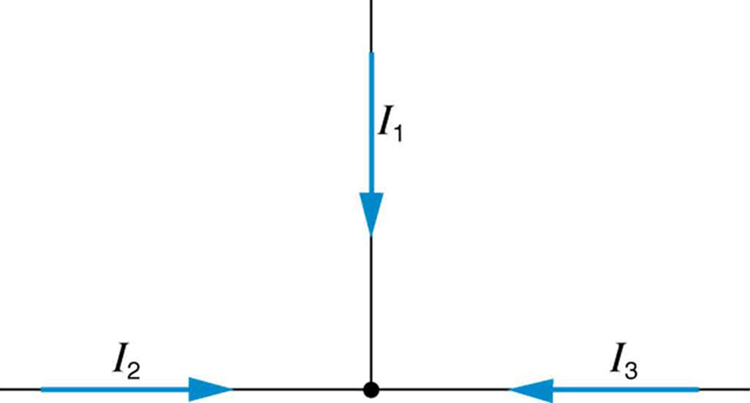
20. Aplique a regra de junção na junção b na Figura. Alguma informação nova é obtida aplicando a regra de junção em e? (Na figura, cada emf é representado pelo script E.)
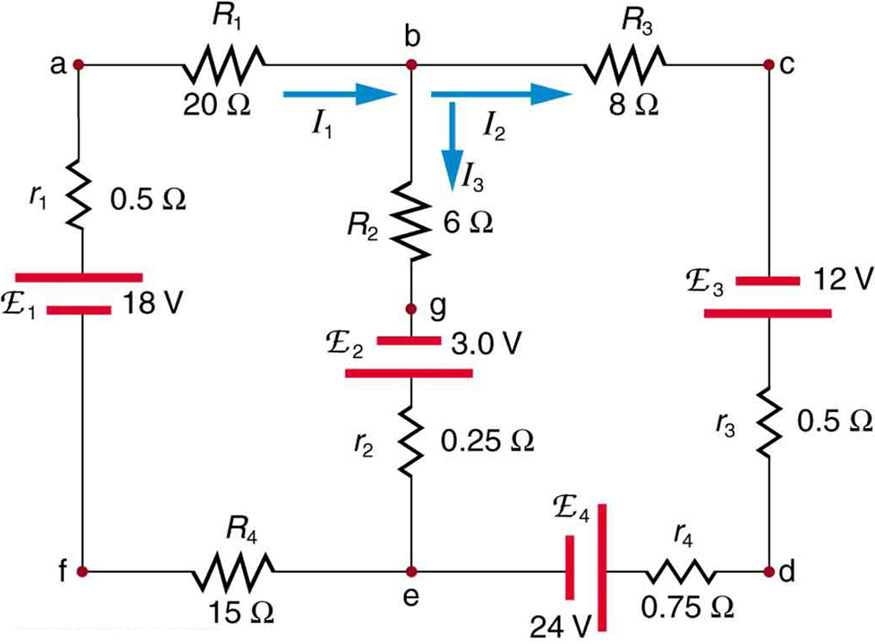
21. (a) Qual é a diferença de potencial indo do ponto a ao ponto b na Figura? (b) Qual é a diferença de potencial indo de c para b? (c) De e para g? (d) De mim para d?
22. Aplique a regra de loop ao loop afedcba na Figura.
23. Aplique a regra de loop aos loops abgefa e cbgedc na Figura.
21.4: Voltímetros e amperímetros DC
24. Por que você não deve conectar um amperímetro diretamente em uma fonte de tensão, conforme mostrado na Figura? (Observe que o script E na figura significa emf.)
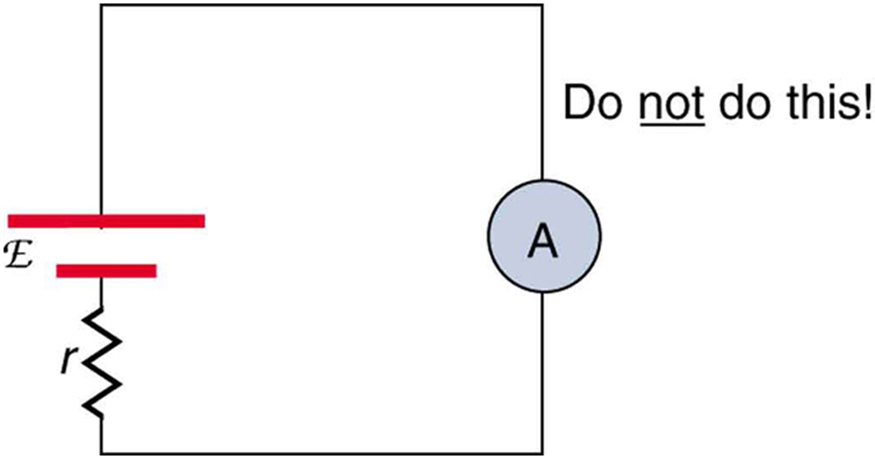
25. Suponha que você esteja usando um multímetro (projetado para medir uma faixa de voltagens, correntes e resistências) para medir a corrente em um circuito e, inadvertidamente, deixá-lo no modo voltímetro. Qual efeito o medidor terá no circuito? O que aconteceria se você estivesse medindo a tensão, mas acidentalmente colocasse o medidor no modo amperímetro?
26. Especifique os pontos aos quais você pode conectar um voltímetro para medir as seguintes diferenças de potencial na Figura:
(a) a diferença de potencial da fonte de tensão;
(b) a diferença de potencial entre eles\(\displaystyle R_1\);
(c) do outro lado\(\displaystyle R_2\);
(d) do outro lado\(\displaystyle R_3\);
(e) do outro lado\(\displaystyle R_2\)\(\displaystyle R_3\) e.
Observe que pode haver mais de uma resposta para cada parte.
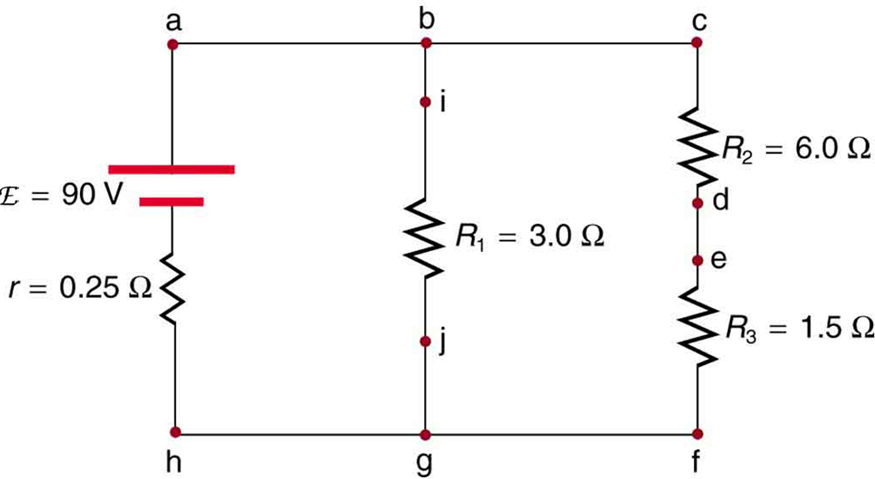
27. Para medir as correntes na Figura, você substituiria um fio entre dois pontos por um amperímetro. Especifique os pontos entre os quais você colocaria um amperímetro para medir o seguinte:
(a) a corrente total;
(b) a corrente que passa\(\displaystyle R_1\);
(c) por meio de\(\displaystyle R_2\);
(d) até\(\displaystyle R_3\).
Observe que pode haver mais de uma resposta para cada parte.
21.5: Medidas nulas
28. Por que uma medição nula pode ser mais precisa do que uma que usa voltímetros e amperímetros padrão? Quais fatores limitam a precisão das medições nulas?
29. Se um potenciômetro é usado para medir emfs de células na ordem de alguns volts, por que é mais preciso que o tamanho padrão do emfs 12 {"emf” rSub {tamanho 8 {s}}} {} seja da mesma ordem de magnitude e que as resistências estejam na faixa de alguns ohms?
21.6: Circuitos DC contendo resistores e capacitores
30. Em relação às unidades envolvidas na relação\(\displaystyle τ=RC\), verifique se as unidades de resistência vezes capacitância são tempo, ou seja,\(\displaystyle Ω⋅F=s\).
31. A constante de\(\displaystyle RC\) tempo na desfibrilação cardíaca é crucial para limitar o tempo em que a corrente flui. Se a capacitância na unidade de desfibrilação for fixa, como você manipularia a resistência no circuito para ajustar a\(\displaystyle RC\) constante\(\displaystyle τ\)? Também seria necessário um ajuste da tensão aplicada para garantir que a corrente fornecida tenha um valor apropriado?
32. Ao fazer uma medição de ECG, é importante medir as variações de tensão em pequenos intervalos de tempo. O tempo é limitado pela\(\displaystyle RC\) constante do circuito — não é possível medir variações de tempo menores do que\(\displaystyle RC\). Como você manipularia\(\displaystyle R\) e entraria\(\displaystyle C\) no circuito para permitir as medições necessárias?
33. Desenhe dois gráficos de carga versus tempo em um capacitor. Desenhe um para carregar um capacitor inicialmente não carregado em série com um resistor, como no circuito da Figura, começando de\(\displaystyle t=0\). Desenhe o outro para descarregar um capacitor através de um resistor, como no circuito da Figura, começando em\(\displaystyle t=0\), com uma carga inicial\(\displaystyle Q_0\). Mostre pelo menos dois intervalos de\(\displaystyle τ\).
34. Ao carregar um capacitor, conforme discutido em conjunto com a Figura, quanto tempo leva para a tensão no capacitor atingir emf? Isso é um problema?
35. Ao descarregar um capacitor, conforme discutido em conjunto com a Figura, quanto tempo leva para que a tensão no capacitor chegue a zero? Isso é um problema?
36. Referindo-se à Figura, desenhe um gráfico da diferença de potencial entre o resistor e o tempo, mostrando pelo menos dois intervalos de\(\displaystyle τ\). Também desenhe um gráfico da corrente versus tempo para essa situação.
37. Um cabo de extensão longo e barato é conectado de dentro da casa a uma geladeira externa. A geladeira não funciona como deveria. Qual pode ser o problema?
38. Na Figura, o gráfico indica que a constante de tempo é menor para descarregar do que para carregar? Você esperaria que o gás ionizado tivesse baixa resistência? Como você se ajustaria\(\displaystyle R\) para ficar mais tempo entre os flashes? O ajuste\(\displaystyle R\) afetaria o tempo de descarga?
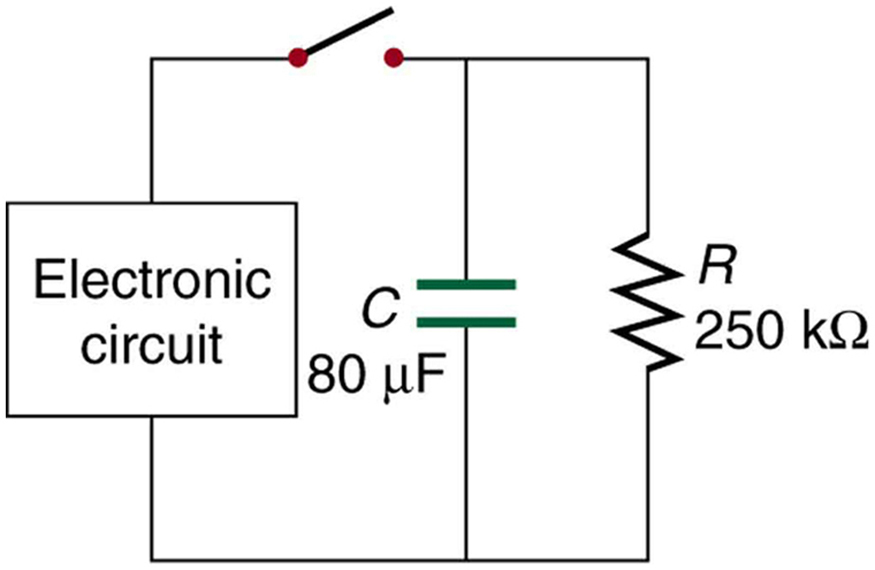
39. Um aparelho eletrônico pode ter grandes capacitores em alta tensão na seção de fonte de alimentação, apresentando risco de choque mesmo quando o aparelho está desligado. Portanto, um “resistor de sangramento” é colocado em tal capacitor, conforme mostrado esquematicamente na Figura, para remover a carga após o aparelho ser desligado. Por que a resistência do purgador deve ser muito maior do que a resistência efetiva do resto do circuito? Como isso afeta a constante de tempo para descarregar o capacitor?
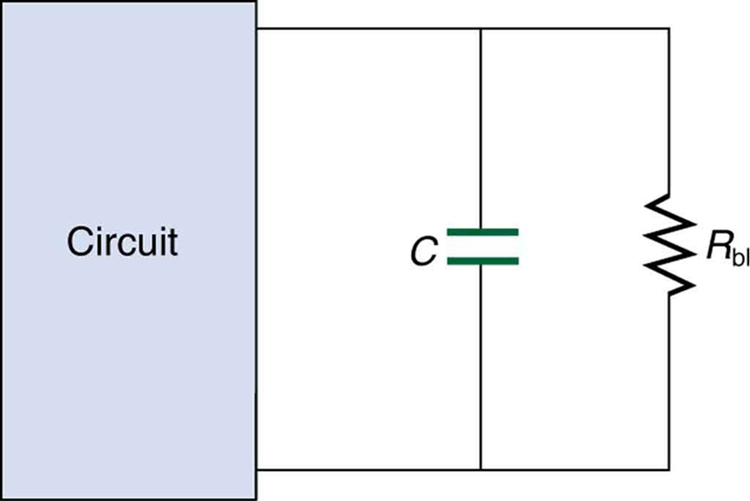
Um resistor de sangramento\(\displaystyle R_{bl}\) descarrega o capacitor neste dispositivo eletrônico assim que ele é desligado.
Problema e exercícios
21.1: Resistores em série e paralelos
Nota: Os dados retirados de figuras podem ser considerados precisos em três dígitos significativos.
40. (a) Qual é a resistência de dez\(\displaystyle 275-Ω\) resistores conectados em série?
(b) Em paralelo?
Solução
(a)\(\displaystyle 2.75kΩ\)
(b)\(\displaystyle 27.5Ω\)
41. (a) Qual é a resistência de\(\displaystyle 1.00×10^2−Ω,\) um\(\displaystyle 2.50-kΩ\) a e de um\(\displaystyle 4.00-kΩ\) resistor conectado em série?
(b) Em paralelo?
42. Quais são as maiores e menores resistências que você pode obter conectando um\(\displaystyle 36.0-Ω\)\(\displaystyle 50.0-Ω\), a e um\(\displaystyle 700-Ω\) resistor?
Solução
(a)\(\displaystyle 786Ω\)
(b)\(\displaystyle 20.3Ω\)
43. Uma torradeira de 1800 W, uma frigideira elétrica de 1400 W e uma lâmpada de 75 W são conectadas à mesma tomada em um circuito de 15 A e 120 V. (Os três dispositivos estão em paralelo quando conectados ao mesmo soquete.).
(a) Qual corrente é consumida por cada dispositivo?
(b) Essa combinação queimará o fusível 15-A?
44. O farol de 30,0 W e o motor de partida de 2,40 kW do seu carro são normalmente conectados em paralelo em um sistema de 12,0 V. Que energia um farol e o motor de partida consumiriam se conectados em série a uma bateria de 12,0 V? (Negligencie qualquer outra resistência no circuito e qualquer alteração na resistência nos dois dispositivos.)
Solução
\(\displaystyle 29.6W\)
45. (a) Com uma bateria de 48,0 V\(\displaystyle 24.0-Ω\) e\(\displaystyle 96.0-Ω\) resistores, encontre a corrente e a potência de cada um quando conectado em série. (b) Repita quando as resistências estiverem em paralelo.
46. Referindo-se ao exemplo que combina circuitos\(\displaystyle I_3\) em série e paralelos e a Figura, calcule das duas maneiras diferentes a seguir:
(a) a partir dos valores conhecidos de\(\displaystyle I\) e\(\displaystyle I_2\);
(b) usando a lei de Ohm para\(\displaystyle R_3\). Em ambas as partes, mostre explicitamente como você segue as etapas nas Estratégias de resolução de problemas para resistores em série e paralelos.
Solução
(a) 0,74 A
(b) 0,742 A
47. Referindo-se à Figura:
(a)\(\displaystyle P_3\) Calcule e observe como ele se compara aos problemas\(\displaystyle P_3\) encontrados nos dois primeiros exemplos de problemas neste módulo.
(b) Encontre a potência total fornecida pela fonte e compare-a com a soma das potências dissipadas pelos resistores.
48. Consulte a Figura e a discussão sobre o escurecimento das luzes quando um aparelho pesado é ligado.
(a) Dado que a fonte de tensão é 120 V, a resistência do fio é e a lâmpada é nominalmente 75,0 W, que potência a lâmpada dissipará se um total de 15,0 A passar pelos fios quando o motor for ligado?\(\displaystyle 0.400Ω\) Suponha uma mudança insignificante na resistência da lâmpada.
(b) Qual energia é consumida pelo motor?
Solução
(a) 60,8 W
(b) 3,18 kW
49. Uma linha de transmissão de energia de 240 kV\(\displaystyle 5.00×10^2A\) é pendurada em torres de metal aterradas por isoladores de cerâmica, cada um com uma\(\displaystyle 1.00×10^9−Ω\) resistência. Figura.
(a) Qual é a resistência ao solo de 100 desses isoladores?
(b) Calcule a potência dissipada por 100 deles.
(c) Que fração da energia transportada pela linha é essa? Mostre explicitamente como você segue as etapas nas Estratégias de resolução de problemas para resistores em série e paralelos.
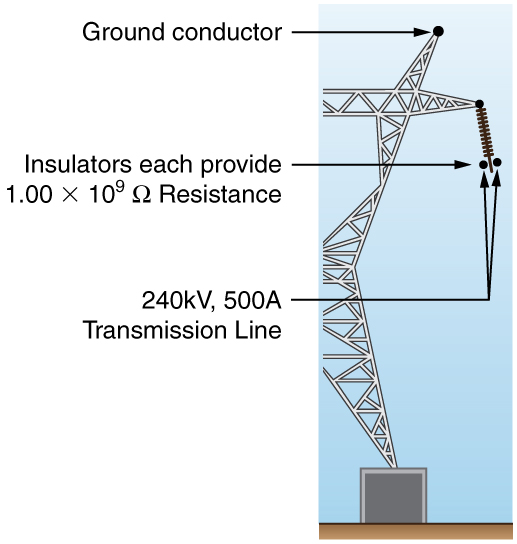
O transporte da linha de transmissão de alta tensão (240 kV)\(\displaystyle 5.00×10^2A\) é pendurado em uma torre de transmissão de metal aterrada. A fileira de isoladores cerâmicos fornece\(\displaystyle 1.00×10^9Ω\) resistência a cada um.
50. \(\displaystyle R_1\)Mostre que se dois resistores\(\displaystyle R_2\) forem combinados e um for muito maior que o outro (\(\displaystyle R_1>>R_2\)):
(a) Sua resistência em série é quase igual à maior resistência\(\displaystyle R_1\).
(b) Sua resistência paralela é quase igual à resistência menor\(\displaystyle R_2\).
Solução
(a)\(\displaystyle R_s=R_1+R_2⇒R_s≈R_1(R_1>>R_2)\)
(b)\(\displaystyle \frac{1}{R_p}=\frac{1}{R_1}+\frac{1}{R_2}=\frac{R_1+R_2}{R_1R_2}\)
para que
\(\displaystyle R_p=\frac{R_1R_2}{R_1+R_2}≈\frac{R_1R_2}{R_1}=R_2(R_1>>R_2)\).
51. Resultados irracionais
Dois resistores, um com uma resistência de\(\displaystyle 145Ω\), são conectados em paralelo para produzir uma resistência total de\(\displaystyle 150Ω\).
(a) Qual é o valor da segunda resistência?
(b) O que não é razoável nesse resultado?
(c) Quais suposições são irracionais ou inconsistentes?
52. Resultados irracionais
Dois resistores, um com uma resistência de\(\displaystyle 900 kΩ\), são conectados em série para produzir uma resistência total de\(\displaystyle 0.500 MΩ\).
(a) Qual é o valor da segunda resistência?
(b) O que não é razoável nesse resultado?
(c) Quais suposições são irracionais ou inconsistentes?
Solução
(a)\(\displaystyle −400 kΩ\)
(b) A resistência não pode ser negativa.
(c) Diz-se que a resistência em série é menor que um dos resistores, mas deve ser maior do que qualquer um dos resistores.
21.2: Força eletromotriz: tensão terminal
53. As baterias automotivas padrão têm seis células de chumbo-ácido em série, criando um emf total de 12,0 V. Qual é o emf de uma célula individual de chumbo-ácido?
Solução
2,00 V
54. As células secas de carbono-zinco (às vezes chamadas de células não alcalinas) têm um emf de 1,54 V e são produzidas como células únicas ou em várias combinações para formar outras voltagens.
(a) Quantas células de 1,54 V são necessárias para fazer com que a bateria comum de 9 V seja usada em muitos pequenos dispositivos eletrônicos?
(b) Qual é o emf real da bateria de aproximadamente 9 V?
(c) Discuta como a resistência interna na conexão em série das células afetará a tensão terminal dessa bateria de aproximadamente 9 V.
55. Qual é a tensão de saída de uma célula de lítio de 3.0000-V em um relógio de pulso digital que consome 0,300 mA, se a resistência interna da célula for\(\displaystyle 2.00Ω\)?
Solução
2.994 V
56. (a) Qual é a tensão terminal de uma grande célula seca de carbono-zinco de 1,54 V usada em um laboratório de física para fornecer 2,00 A a um circuito, se a resistência interna da célula for\(\displaystyle 0.100 Ω\)?
(b) Quanta energia elétrica a célula produz?
(c) Qual energia vai para sua carga?
57. Qual é a resistência interna de uma bateria de automóvel que tem um emf de 12,0 V e uma tensão terminal de 15,0 V enquanto uma corrente de 8,00 A a carrega?
Solução
\(\displaystyle 0.375Ω\)
58. (a) Encontre a tensão terminal de uma bateria de motocicleta de 12,0 V com resistência\(\displaystyle 0.600-Ω\) interna, se estiver sendo carregada por uma corrente de 10,0 A.
(b) Qual é a tensão de saída do carregador de bateria?
59. Uma bateria de carro com um emf de 12 V e uma resistência interna de\(\displaystyle 0.050Ω\) está sendo carregada com uma corrente de 60 A. Observe que neste processo a bateria está sendo carregada.
(a) Qual é a diferença de potencial entre seus terminais?
(b) Em que taxa a energia térmica está sendo dissipada na bateria?
(c) Em que ritmo a energia elétrica está sendo convertida em energia química?
(d) Quais são as respostas para (a) e (b) quando a bateria é usada para fornecer 60 A ao motor de partida?
60. A resistência ao calor de uma lâmpada de lanterna é\(\displaystyle 2.30Ω\), e ela é operada por uma célula alcalina de 1,58 V com uma resistência\(\displaystyle 0.100-Ω\) interna.
(a) Que corrente flui?
(b) Calcule a energia fornecida à lâmpada usando\(\displaystyle I^2R_{bulb}\).
(c) Essa potência é a mesma calculada usando\(\displaystyle \frac{V^2}{R_{bulb}}\)?
Solução
(a) 0,658 A
(b) 0,997 W
(c) 0,997 W; sim
61. A etiqueta em um rádio portátil recomenda o uso de células recarregáveis de níquel-cádmio (nicads), embora tenham um emf de 1,25 V, enquanto as células alcalinas tenham um emf de 1,58 V. O rádio tem uma\(\displaystyle 3.20-Ω\) resistência.
(a) Desenhe um diagrama do circuito do rádio e suas baterias. Agora, calcule a potência fornecida ao rádio.
(b) Ao usar células Nicad, cada uma com uma resistência interna de\(\displaystyle 0.0400 Ω\).
(c) Ao usar células alcalinas, cada uma com uma resistência interna de\(\displaystyle 0.200 Ω\).
(d) Essa diferença parece significativa, considerando que a resistência efetiva do rádio é reduzida quando o volume aumenta?
62. Um motor de partida de automóvel tem uma resistência equivalente\(\displaystyle 0.0500Ω\) e é fornecido por uma bateria de 12,0 V com resistência\(\displaystyle 0.0100-Ω\) interna.
(a) Qual é a corrente do motor?
(b) Qual tensão é aplicada a ele?
(c) Qual energia é fornecida ao motor?
(d) Repita esses cálculos quando as conexões da bateria estiverem corroídas e adicionadas\(\displaystyle 0.0900Ω\) ao circuito. (Problemas significativos são causados até mesmo por pequenas quantidades de resistência indesejada em aplicações de baixa tensão e alta corrente.)
Solução
(a) 200 A
(b) 10,0 V
(c) 2,00 kW
(d)\(\displaystyle 0.1000Ω;80.0 A, 4.0 V, 320 W\)
63. Um brinquedo eletrônico infantil é fornecido por três células alcalinas de 1,58 V com resistências internas\(\displaystyle 0.0200Ω\) em série, com uma célula seca de carbono-zinco de 1,53 V com resistência\(\displaystyle 0.100-Ω\) interna. A resistência da carga é\(\displaystyle 10.0Ω\).
(a) Desenhe um diagrama de circuito do brinquedo e suas baterias
(b) Quais fluxos de corrente?
(c) Quanta energia é fornecida à carga?
(d) Qual é a resistência interna da célula seca se ela ficar ruim, resultando em apenas 0,500 W sendo fornecidos à carga?
64. (a) Qual é a resistência interna de uma fonte de tensão se a tensão do terminal cair em 2,00 V quando a corrente fornecida aumenta em 5,00 A?
(b) O emf da fonte de tensão pode ser encontrado com as informações fornecidas?
Solução
(a)\(\displaystyle 0.400 Ω\)
(b) Não, há apenas uma equação independente, então só\(\displaystyle r\) pode ser encontrada.
65. Uma pessoa com resistência corporal entre as mãos agarra\(\displaystyle 10.0kΩ\) acidentalmente os terminais de uma fonte de alimentação de 20,0 kV. (NÃO faça isso!)
(a) Desenhe um diagrama de circuito para representar a situação.
(b) Se a resistência interna da fonte de alimentação for\(\displaystyle 2000Ω\), qual é a corrente através de seu corpo?
(c) Qual é o poder dissipado em seu corpo?
(d) Se a fonte de alimentação deve ser tornada segura aumentando sua resistência interna, qual deve ser a resistência interna para que a corrente máxima nessa situação seja de 1,00 mA ou menos?
(e) Essa modificação comprometerá a eficácia da fonte de alimentação para acionar dispositivos de baixa resistência? Explique seu raciocínio.
66. Peixes elétricos geram corrente com células biológicas chamadas eletroplacas, que são dispositivos fisiológicos de emf. As placas elétricas da enguia sul-americana estão dispostas em 140 fileiras, cada fileira se estendendo horizontalmente ao longo do corpo e cada uma contendo 5000 eletroplacas. Cada placa elétrica tem um emf de 0,15 V e resistência interna de\(\displaystyle 0.25Ω\). Se a água ao redor do peixe tem resistência de\(\displaystyle 800Ω\), quanta corrente a enguia pode produzir na água de perto de sua cabeça até perto de sua cauda?
67. Conceitos integrados
Uma bateria automotiva emf de 12,0 V tem uma tensão terminal de 16,0 V quando é carregada por uma corrente de 10,0 A.
(a) Qual é a resistência interna da bateria?
(b) Qual energia é dissipada dentro da bateria?
(c) Em que taxa (in\(\displaystyle ºC/min\)) sua temperatura aumentará se sua massa for de 20,0 kg e tiver um calor específico de\(\displaystyle 0.300kcal/kg⋅ºC\), supondo que nenhum calor escape?
68. Resultados irracionais
Uma célula alcalina de 1,58 V com resistência\(\displaystyle 0.200-Ω\) interna está fornecendo 8,50 A a uma carga.
(a) Qual é a tensão do terminal?
(b) Qual é o valor da resistência da carga?
(c) O que não é razoável nesses resultados?
(d) Quais suposições são irracionais ou inconsistentes?
Solução
(a) —0,120 V
(b)\(\displaystyle −1.41×10^{−2}Ω\)
(c) Tensão terminal negativa; resistência de carga negativa.
(d) A suposição de que tal célula poderia fornecer 8,50 A é inconsistente com sua resistência interna.
69. Resultados irracionais
(a) Qual é a resistência interna de uma célula seca de 1,54 V que fornece 1,00 W de energia a uma\(\displaystyle 15.0-Ω\) lâmpada?
(b) O que não é razoável nesse resultado?
(c) Quais suposições são irracionais ou inconsistentes?
21.3: Regras de Kirchhoff
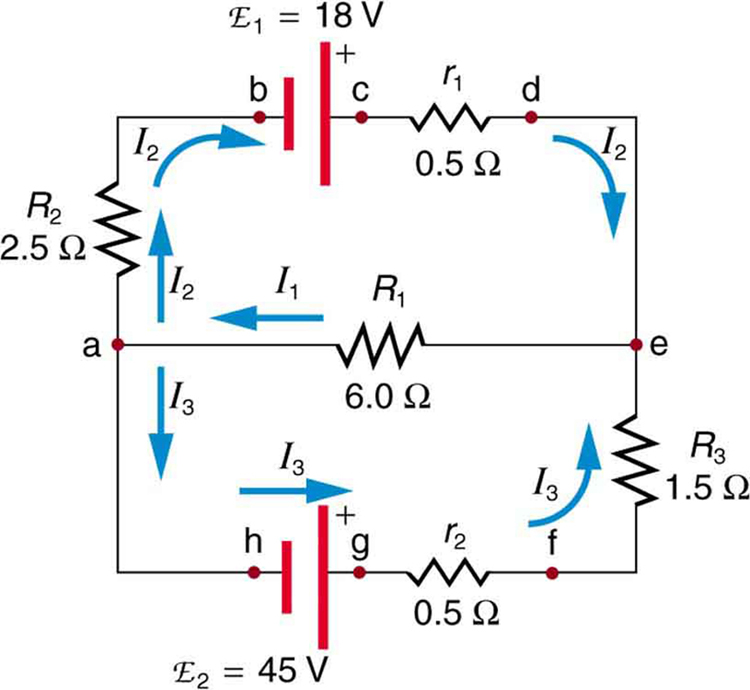
70. Aplique a regra de loop ao loop abcdefgha na Figura.
Solução
\(\displaystyle −I_2R_2+emf_1−I_2r_1+I_3R_3+I_3r_2−emf_2=0\)
71. Aplique a regra de loop ao loop aedcba na Figura na Pergunta 70.
72. Verifique a segunda equação no Exemplo substituindo os valores encontrados pelas correntes\(\displaystyle I_1\)\(\displaystyle I_2\) e.
73. Verifique a terceira equação no Exemplo substituindo os valores encontrados pelas correntes\(\displaystyle I_1\)\(\displaystyle I_3\) e.
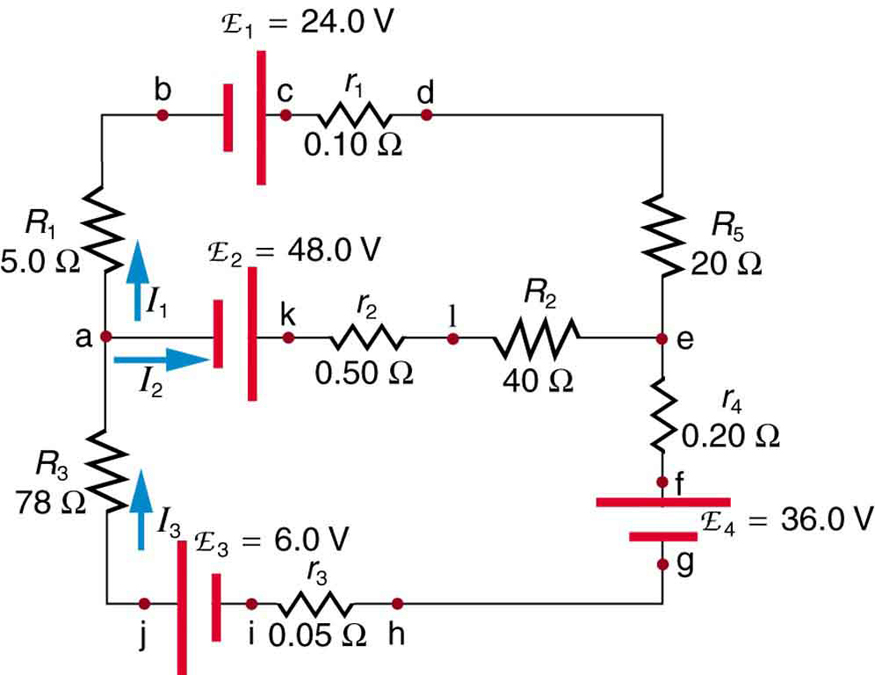
74. Aplique a regra de junção no ponto a da Figura.
Solução
\(\displaystyle I_3=I_1+I_2\)
75. Aplique a regra de loop ao loop abcdefghija na Figura na Pergunta 74.
76. Aplique a regra de loop ao loop akledcba na Figura na Pergunta 74.
Solução
\(\displaystyle emf_2−I_2r_2−I_2R_2+I_1R_5+I_1r_1−emf_1+I_1R_1=0\)
77. Encontre as correntes que fluem no circuito na Figura da Pergunta 74. Mostre explicitamente como você segue as etapas nas Estratégias de resolução de problemas para resistores em série e paralelos.
78. Resolva o exemplo, mas use o loop abcdefgha em vez do loop akledcba. Mostre explicitamente como você segue as etapas nas Estratégias de resolução de problemas para resistores em série e paralelos.
Solução
(a)\(\displaystyle I_1=4.75 A\)
(b)\(\displaystyle I_2=−3.5 A\)
(c)\(\displaystyle I_3=8.25 A\)
79. Encontre as correntes que fluem no circuito na Figura.

80. Resultados irracionais
Considere o circuito na Figura e suponha que os emfs sejam desconhecidos e que as correntes sejam\(\displaystyle I_1=5.00 A, I_2=3.0 A\),\(\displaystyle I_3=–2.00 A\) e.
(a) Você conseguiu encontrar os emfs?
(b) O que há de errado com as suposições?
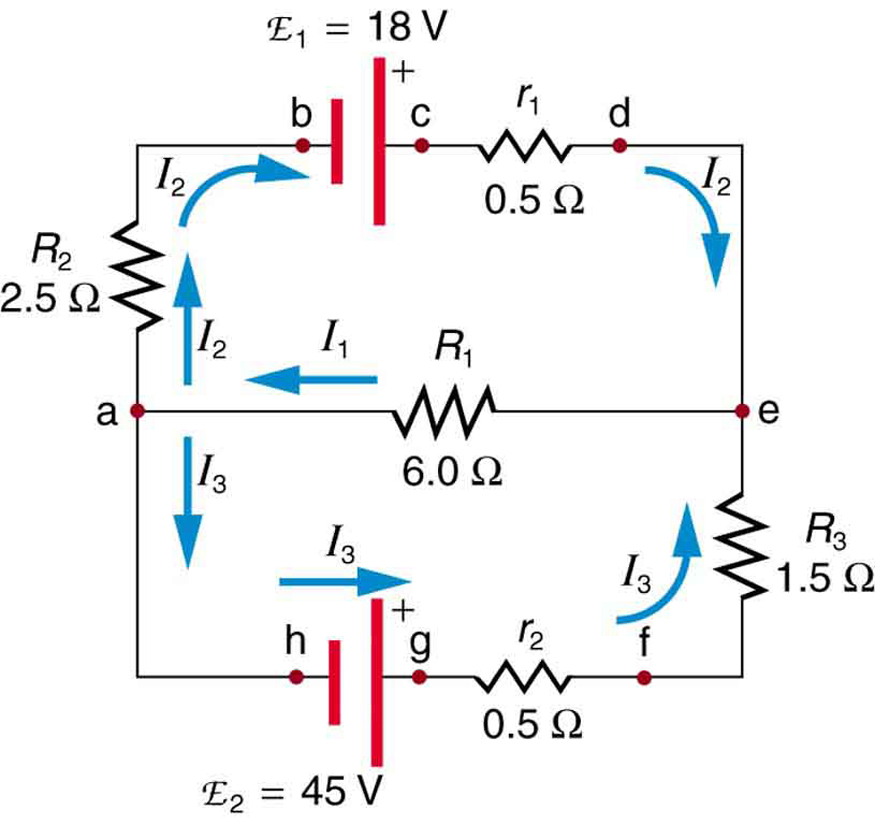
Solução
(a) Não, você obteria equações inconsistentes para resolver.
(b)\(\displaystyle I_1≠I_2+I_3\). As correntes assumidas violam a regra de junção.
21.4: Voltímetros e amperímetros DC
81. Qual é a sensibilidade do galvanômetro (ou seja, qual corrente fornece uma deflexão em grande escala) dentro de um voltímetro que tem uma\(\displaystyle 1.00-MΩ\) resistência em sua escala de 30,0 V?
Solução
\(\displaystyle 30μA\)
82. Qual é a sensibilidade do galvanômetro (ou seja, qual corrente fornece uma deflexão em grande escala) dentro de um voltímetro que tem uma\(\displaystyle 25.0-kΩ\) resistência em sua escala de 100 V?
83. Encontre a resistência que deve ser colocada em série com um\(\displaystyle 25.0-Ω\) galvanômetro com uma\(\displaystyle 50.0-μA\) sensibilidade (a mesma que a discutida no texto) para permitir que ele seja usado como um voltímetro com uma leitura em escala real de 0,100 V.
Solução
\(\displaystyle 1.98 kΩ\)
84. Encontre a resistência que deve ser colocada em série com um\(\displaystyle 25.0-Ω\) galvanômetro com uma\(\displaystyle 50.0-μA\) sensibilidade (a mesma que a discutida no texto) para permitir que ele seja usado como um voltímetro com uma leitura em escala real de 3000 V. Inclua um diagrama de circuito com sua solução.
85. Encontre a resistência que deve ser colocada em paralelo com um\(\displaystyle 25.0-Ω\) galvanômetro com uma\(\displaystyle 50.0-μA\) sensibilidade (a mesma discutida no texto) para permitir que ele seja usado como um amperímetro com uma leitura em escala real de 10,0 A. Inclua um diagrama de circuito com sua solução.
Solução
\(\displaystyle 1.25×10^{−4}Ω\)
86. Encontre a resistência que deve ser colocada em paralelo com um\(\displaystyle 25.0-Ω\) galvanômetro com uma\(\displaystyle 50.0-μA\) sensibilidade (a mesma discutida no texto) para permitir que ele seja usado como um amperímetro com uma leitura em escala real de 300 mA.
87. Encontre a resistência que deve ser colocada em série com um\(\displaystyle 10.0-Ω\) galvanômetro com uma\(\displaystyle 100-μA\) sensibilidade para permitir que ele seja usado como um voltímetro com:
(a) uma leitura em grande escala de 300 V e
(b) uma leitura em escala real de 0,300 V.
Solução
(a)\(\displaystyle 3.00 MΩ\)
(b)\(\displaystyle 2.99 kΩ\)
88. Encontre a resistência que deve ser colocada em paralelo com um\(\displaystyle 10.0-Ω\) galvanômetro com uma\(\displaystyle 100-μA\) sensibilidade para permitir que ele seja usado como um amperímetro com:
(a) uma leitura em grande escala de 20,0 A, e
(b) uma leitura em grande escala de 100 mA.
89. Suponha que você meça a tensão terminal de uma célula alcalina de 1,585 V com uma resistência interna de\(\displaystyle 0.100Ω\) colocando um\(\displaystyle 1.00-kΩ\) voltímetro em seus terminais. (Veja a Figura.)
(a) Que corrente flui?
(b) Encontre a tensão do terminal.
(c) Para ver a proximidade da tensão terminal medida do emf, calcule sua proporção.
Solução
(a) 1,58 mA
(b) 1,5848 V (são necessários quatro dígitos para ver a diferença)
(c) 0,99990 (são necessários cinco dígitos para ver a diferença da unidade)
90. Suponha que você meça a tensão terminal de uma célula de lítio de 3.200 V com uma resistência interna de\(\displaystyle 5.00Ω\) colocando um\(\displaystyle 1.00-kΩ\) voltímetro em seus terminais.
(a) Que corrente flui?
(b) Encontre a tensão do terminal.
(c) Para ver a proximidade da tensão terminal medida do emf, calcule sua proporção.
91. Um determinado amperímetro tem uma resistência de\(\displaystyle 5.00×10^{−5}Ω\) 3,00-A e contém um\(\displaystyle 10.0-Ω\) galvanômetro. Qual é a sensibilidade do galvanômetro?
Solução
\(\displaystyle 15.0 μA\)
92. Um\(\displaystyle 1.00-MΩ\) voltímetro é colocado em paralelo com um\(\displaystyle 75.0-kΩ\) resistor em um circuito.
(a) Desenhe um diagrama de circuito da conexão.
(b) Qual é a resistência da combinação?
(c) Se a tensão na combinação for mantida a mesma que era apenas no\(\displaystyle 75.0-kΩ\) resistor, qual é o aumento percentual na corrente?
(d) Se a corrente através da combinação for mantida a mesma que era apenas através do\(\displaystyle 75.0-kΩ\) resistor, qual é a diminuição percentual na tensão?
(e) As mudanças encontradas nas partes (c) e (d) são significativas? Discuta.
93. Um\(\displaystyle 0.0200-Ω\) amperímetro é colocado em série com um\(\displaystyle 10.00-Ω\) resistor em um circuito.
(a) Desenhe um diagrama de circuito da conexão.
(b) Calcule a resistência da combinação.
(c) Se a tensão for mantida a mesma em toda a combinação e somente através do\(\displaystyle 10.00-Ω\) resistor, qual é a diminuição percentual na corrente?
(d) Se a corrente for mantida a mesma através da combinação e somente através do\(\displaystyle 10.00-Ω\) resistor, qual é o aumento percentual na tensão?
(e) As mudanças encontradas nas partes (c) e (d) são significativas? Discuta.
Solução
(a)

(b)\(\displaystyle 10.02Ω\)
(c) 0,9980, ou uma redução\(\displaystyle 2.0×10^{–1}\) percentual
(d) 1,002, ou um aumento\(\displaystyle 2.0×10^{–1}\) percentual
(e) Não significativo.
94. Resultados irracionais
Suponha que você tenha um\(\displaystyle 40.0-Ω\) galvanômetro com\(\displaystyle 25.0-μA\) sensibilidade.
(a) Que resistência você colocaria em série para permitir que ele seja usado como um voltímetro com uma deflexão em grande escala de 0,500 mV?
(b) O que não é razoável nesse resultado?
(c) Quais suposições são responsáveis?
95. Resultados irracionais
(a) Que resistência você colocaria em paralelo com um\(\displaystyle 40.0-Ω\) galvanômetro com uma sensibilidade de 25,0 μA para permitir que ele seja usado como um amperímetro com deflexão em grande escala\(\displaystyle 10.0-μA\)?
(b) O que não é razoável nesse resultado?
(c) Quais suposições são responsáveis?
Solução
(a)\(\displaystyle −66.7Ω\)
(b) Você não pode ter resistência negativa.
(c) Não é razoável que\(\displaystyle I_G\) seja maior do que\(\displaystyle I_{tot}\) (veja a Figura). Você não pode obter uma deflexão em grande escala usando uma corrente menor que a sensibilidade do galvanômetro.
21.5: Medidas nulas
96. O que é a\(\displaystyle emf_x\) célula sendo medida em um potenciômetro, se a emf da célula padrão for 12,0 V e o potenciômetro for balanceado para\(\displaystyle R_x=5.000Ω\) e\(\displaystyle R_s=2.500Ω\)?
Solução
24,0 V
97. Calcule o\(\displaystyle emf_x\) de uma célula seca para a qual um potenciômetro está balanceado quando\(\displaystyle R_x=1.200Ω\), enquanto uma célula padrão alcalina com um emf de 1.600 V\(\displaystyle R_s=1.247Ω\) precisa equilibrar o potenciômetro.
98. Quando uma resistência desconhecida\(\displaystyle R_x\) é colocada em uma ponte de Wheatstone, é possível equilibrar a ponte ajustando-a\(\displaystyle R_3\) para ser\(\displaystyle 2500Ω\). O que é\(\displaystyle R_x\) se\(\displaystyle \frac{R_2}{R_1}=0.625\)?
Solução
\(\displaystyle 1.56 kΩ\)
99. A que valor você deve ajustar\(\displaystyle R_3\) para equilibrar uma ponte de Wheatstone, se a resistência desconhecida for\(\displaystyle R_x\)\(\displaystyle 100Ω, R1\) é\(\displaystyle 50.0Ω\) e\(\displaystyle R_2\) é\(\displaystyle 175Ω\)?
100. (a) O que é desconhecido\(\displaystyle emf_x\) em um potenciômetro que equilibra quando\(\displaystyle R_x\) é\(\displaystyle 10.0Ω\) e equilibra quando\(\displaystyle R_s\) é\(\displaystyle 15.0Ω\) para um emf padrão de 3.000 V?
(b) O mesmo\(\displaystyle emf_x\) é colocado no mesmo potenciômetro, que agora se equilibra quando\(\displaystyle R_s\) é\(\displaystyle 15.0Ω\) para um emf padrão de 3.100 V. Em que resistência o potenciômetro\(\displaystyle R_x\) se equilibra?
Solução
(a) 2,00 V
(b)\(\displaystyle 9.68Ω\)
101. Suponha que você queira medir as resistências na faixa de\(\displaystyle 10.0Ω\) até\(\displaystyle 10.0 kΩ\) o uso de uma ponte de Wheatstone que tenha\(\displaystyle \frac{R_2}{R_1}=2.000\). Em qual faixa deve\(\displaystyle R_3\) ser ajustável?
Faixa de solução = 5,00Ω a 5,00kΩ
21.6: Circuitos DC contendo resistores e capacitores
102. O dispositivo de temporização no sistema de limpador intermitente de um automóvel é baseado em uma constante de\(\displaystyle RC\) tempo e utiliza um\(\displaystyle 0.500-μF\) capacitor e um resistor variável. Acima de qual faixa deve\(\displaystyle R\) ser feita para variar para atingir constantes de tempo de 2,00 a 15,0 s?
Faixa de soluções\(\displaystyle 4.00\) para\(\displaystyle 30.0 MΩ\)
103. Um marcapasso cardíaco dispara 72 vezes por minuto, cada vez que um capacitor de 25,0 nF é carregado (por uma bateria em série com um resistor) até 0,632 de sua voltagem total. Qual é o valor da resistência?
104. A duração de um flash fotográfico está relacionada a uma constante de\(\displaystyle RC\) tempo, que é\(\displaystyle 0.100 μs\) para uma determinada câmera.
(a) Se a resistência da lâmpada de flash for\(\displaystyle 0.0400Ω\) durante a descarga, qual é o tamanho do capacitor que fornece sua energia?
(b) Qual é a constante de tempo para carregar o capacitor, se a resistência de carregamento for\(\displaystyle 800kΩ\)?
Solução
(a)\(\displaystyle 2.50 μF\)
(b) 2.00 s
105. Um capacitor de 2,00 e um\(\displaystyle 7.50-μF\) capacitor podem ser conectados em série ou em paralelo, assim como um 25,0 e um\(\displaystyle 100-kΩ\) resistor. Calcule as quatro constantes de\(\displaystyle RC\) tempo possíveis ao conectar a capacitância e a resistência resultantes em série.
106. Depois de duas constantes de tempo, qual porcentagem da tensão final, emf, está em um capacitor inicialmente descarregado\(\displaystyle C\), carregado por meio de uma resistência\(\displaystyle R\)?
Solução
86,5%
107. Um\(\displaystyle 500-Ω\) resistor, um\(\displaystyle 1.50-μF\) capacitor sem carga e um emf de 6,16 V são conectados em série.
(a) Qual é a corrente inicial?
(b) Qual é a constante de\(\displaystyle RC\) tempo?
(c) Qual é a corrente após uma constante de tempo?
(d) Qual é a tensão no capacitor após uma constante de tempo?
108. Um desfibrilador cardíaco usado em um paciente tem uma constante de\(\displaystyle RC\) tempo de 10,0 ms devido à resistência do paciente e à capacitância do desfibrilador.
(a) Se o desfibrilador tiver uma\(\displaystyle 8.00-μF\) capacitância, qual é a resistência do caminho pelo paciente? (Você pode negligenciar a capacitância do paciente e a resistência do desfibrilador.)
(b) Se a tensão inicial for de 12,0 kV, quanto tempo leva para diminuir para\(\displaystyle 6.00×10^2V\)?
Solução
(a)\(\displaystyle 1.25 kΩ\)
(b) 30,0 ms
109. Um monitor de ECG deve ter uma constante de\(\displaystyle RC\) tempo menor do que\(\displaystyle 1.00×10^2μs\) para ser capaz de medir variações na tensão em pequenos intervalos de tempo.
(a) Se a resistência do circuito (devida principalmente à do tórax do paciente) for\(\displaystyle 1.00 kΩ\), qual é a capacitância máxima do circuito?
(b) Seria difícil, na prática, limitar a capacitância a menos do que o valor encontrado em (a)?
110. A figura mostra como um resistor de sangramento é usado para descarregar um capacitor depois que um dispositivo eletrônico é desligado, permitindo que uma pessoa trabalhe nos componentes eletrônicos com menos risco de choque.
(a) Qual é a constante de tempo?
(b) Quanto tempo será necessário para reduzir a tensão no capacitor para 0,250% (5% de 5%) de seu valor total quando a descarga começar?
(c) Se o capacitor for carregado até uma tensão\(\displaystyle V_0\) por meio de uma\(\displaystyle 100-Ω\) resistência, calcule o tempo necessário para subir até\(\displaystyle 0.865V_0\) (Isso é cerca de duas constantes de tempo).
Solução
(a) 20,0 s
(b) 120 s
(c) 16,0 ms
111. Usando o tratamento exponencial exato, descubra quanto tempo é necessário para descarregar um\(\displaystyle 250-μF\) capacitor através de um\(\displaystyle 500-Ω\) resistor até 1,00% de sua tensão original.
112. Usando o tratamento exponencial exato, descubra quanto tempo é necessário para carregar um capacitor inicialmente descarregado de 100 pF por meio de um\(\displaystyle 75.0-MΩ\) resistor até 90,0% de sua tensão final.
Solução
\(\displaystyle 1.73×10^{−2}s\)
113. Conceitos integrados
Se você quiser tirar uma foto de uma bala viajando a 500 m/s, um breve flash de luz produzido por uma\(\displaystyle RC\) descarga através de um tubo de flash pode limitar o embaçamento. Supondo que 1,00 mm de movimento durante uma\(\displaystyle RC\) constante seja aceitável, e dado que o flash é acionado por um\(\displaystyle 600-μF\) capacitor, qual é a resistência no tubo do flash?
Solução
\(\displaystyle 3.33×10^{−3}Ω\)
114. Conceitos integrados
Uma lâmpada intermitente em um brinco de Natal é baseada na\(\displaystyle RC\) descarga de um capacitor por meio de sua resistência. A duração efetiva do flash é de 0,250 s, durante a qual ele produz uma média de 0,500 W a partir de uma média de 3,00 V.
(a) Que energia ela dissipa?
(b) Quanta carga se move através da lâmpada?
(c) Encontre a capacitância.
(d) Qual é a resistência da lâmpada?
115. Conceitos integrados
Um\(\displaystyle 160-μF\) capacitor carregado a 450 V é descarregado por meio de um\(\displaystyle 31.2-kΩ\) resistor.
(a) Encontre a constante de tempo.
(b) Calcule o aumento de temperatura do resistor, dado que sua massa é de 2,50 g e seu calor específico é\(\displaystyle 1.67\frac{kJ}{kg⋅ºC}\), observando que a maior parte da energia térmica é retida no curto espaço de tempo da descarga.
(c) Calcule a nova resistência, assumindo que é carbono puro.
(d) Essa mudança na resistência parece significativa?
Solução
(a) 4,99 s
(b)\(\displaystyle 3.87ºC\)
(c)\(\displaystyle 31.1 kΩ\)
(d) Não
116. Resultados irracionais
(a) Calcule a capacitância necessária para obter uma constante de\(\displaystyle RC\) tempo\(\displaystyle 1.00×10^3s\) com um\(\displaystyle 0.100-Ω\) resistor.
(b) O que não é razoável nesse resultado?
(c) Quais suposições são responsáveis?
117. Construa seu próprio problema
Considere a unidade de flash de uma câmera. Crie um problema no qual você calcule o tamanho do capacitor que armazena energia para a lâmpada do flash. Entre as coisas a serem consideradas estão a tensão aplicada ao capacitor, a energia necessária no flash e a carga associada necessária no capacitor, a resistência da lâmpada do flash durante a descarga e a constante de tempo desejada do tamanho RC 12 {ital “RC"} {}.
118. Construa seu próprio problema
Considere uma célula de lítio recarregável que deve ser usada para alimentar uma câmera de vídeo. Crie um problema no qual você calcule a resistência interna da célula durante a operação normal. Além disso, calcule a saída de tensão mínima de um carregador de bateria a ser usado para recarregar sua célula de lítio. Entre as coisas a serem consideradas estão o emf e a tensão terminal útil de uma célula de lítio e a corrente que ela deve ser capaz de fornecer a uma câmera de vídeo.

