16.10: Superposição e interferência

Last updated
Save as PDF

Page ID: 194440

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Explique as ondas estacionárias.
Descreva a representação matemática dos sobretons e da frequência da batida.

A maioria das ondas não parece muito simples. Eles se parecem mais com as ondas na Figura\(\PageIndex{1}\) do que com a simples onda de água considerada em Ondas. (Ondas simples podem ser criadas por uma simples oscilação harmônica e, portanto, ter uma forma senoidal). Ondas complexas são mais interessantes, até bonitas, mas parecem formidáveis. A maioria das ondas parece complexa porque elas resultam da soma de várias ondas simples. Felizmente, as regras para adicionar ondas são bem simples.

A superfície da água de um rio é mostrada, com montanhas ao fundo. Existem pequenas ondulações sobre a superfície da água. — Figura\(\PageIndex{1}\): Essas ondas resultam da superposição de várias ondas de diferentes fontes, produzindo um padrão complexo. (crédito: waterborough, Wikimedia Commons)

Quando duas ou mais ondas chegam ao mesmo ponto, elas se sobrepõem uma à outra. Mais especificamente, os distúrbios das ondas se sobrepõem quando elas se juntam — um fenômeno chamado superposição. Cada perturbação corresponde a uma força, e as forças se somam. Se os distúrbios estiverem na mesma linha, a onda resultante é uma simples adição dos distúrbios das ondas individuais, ou seja, suas amplitudes aumentam. A figura\(\PageIndex{2}\) e a figura\(\PageIndex{3}\) ilustram a superposição em dois casos especiais, os quais produzem resultados simples.

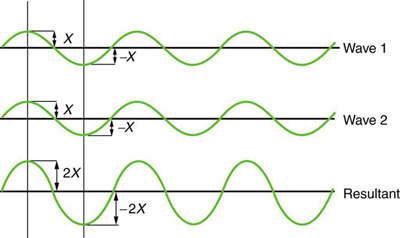
A figura\(\PageIndex{2}\) mostra duas ondas idênticas que chegam ao mesmo ponto exatamente na fase. As cristas das duas ondas estão alinhadas com precisão, assim como as calhas. Essa superposição produz pura interferência construtiva. Como os distúrbios aumentam, a interferência construtiva pura produz uma onda que tem o dobro da amplitude das ondas individuais, mas tem o mesmo comprimento de onda.

O gráfico mostra duas ondas idênticas que chegam ao mesmo ponto exatamente em fase. As cristas das duas ondas estão alinhadas com precisão, assim como as calhas. A amplitude de cada onda é X. Ela produz uma onda construtiva pura. Os distúrbios se somam, resultando em uma nova onda com o dobro da amplitude das ondas individuais, que é dois X, mas com o mesmo comprimento de onda. — Figura\(\PageIndex{2}\): A interferência construtiva pura de duas ondas idênticas produz uma com o dobro da amplitude, mas com o mesmo comprimento de onda.

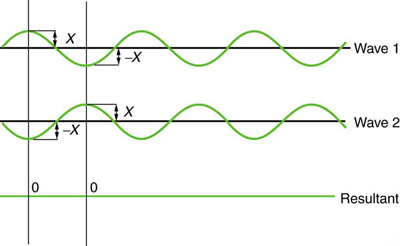
\(\PageIndex{3}\)A figura mostra duas ondas idênticas que chegam exatamente fora de fase, ou seja, alinhadas com precisão da crista à calha, produzindo pura interferência destrutiva. Como os distúrbios estão na direção oposta para essa superposição, a amplitude resultante é zero para pura interferência destrutiva — as ondas se cancelam completamente.

O gráfico mostra duas ondas idênticas que chegam exatamente fora de fase. As cristas de uma onda estão alinhadas com a calha de outra onda. Cada onda tem amplitude igual a X. Como os distúrbios estão em direções opostas, eles se anulam, resultando em uma amplitude zero que é mostrada como a terceira figura mostrando uma linha reta verde, ou seja, as ondas se cancelam produzindo pura interferência destrutiva. — Figura\(\PageIndex{3}\): A interferência destrutiva pura de duas ondas idênticas produz amplitude zero ou cancelamento completo.

Embora ocorram interferências puramente construtivas e destrutivas, elas exigem ondas idênticas alinhadas com precisão. A superposição da maioria das ondas produz uma combinação de interferência construtiva e destrutiva e pode variar de um lugar para outro e de tempos em tempos. O som de um aparelho de som, por exemplo, pode ser alto em um local e baixo em outro. O volume variável significa que as ondas sonoras aumentam parcialmente de forma construtiva e parcialmente destrutiva em locais diferentes. Um aparelho de som tem pelo menos dois alto-falantes criando ondas sonoras, e as ondas podem ser refletidas nas paredes. Todas essas ondas se sobrepõem. Um exemplo de sons que variam ao longo do tempo, de construtivos a destrutivos, é encontrado no ruído combinado de jatos de avião ouvidos por um passageiro parado. O som combinado pode variar para cima e para baixo em volume, pois o som dos dois motores varia no tempo, de construtivo a destrutivo. Esses exemplos são de ondas semelhantes.

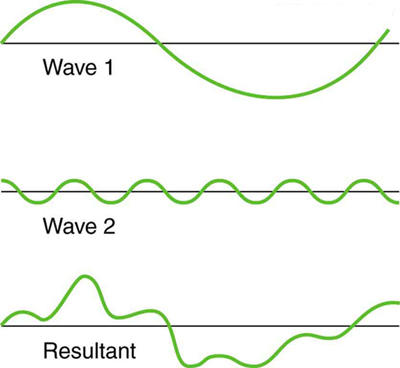
Um exemplo da superposição de duas ondas diferentes é mostrado na Figura\(\PageIndex{4}\). Aqui, novamente, os distúrbios somam e subtraem, produzindo uma onda de aparência mais complicada.

O gráfico mostra duas ondas não idênticas com frequências e comprimentos de onda diferentes. No primeiro gráfico, apenas uma crista e uma calha da onda são vistas. Na segunda figura, cinco cristas são vistas no mesmo comprimento. Quando se sobrepõem, a perturbação soma e subtrai, produzindo uma onda de aparência mais complicada com amplitude e comprimento de onda altamente irregulares devido ao efeito combinado de interferência construtiva e destrutiva. — Figura\(\PageIndex{4}\): A superposição de ondas não idênticas exibe interferência construtiva e destrutiva.

Ondas estacionárias

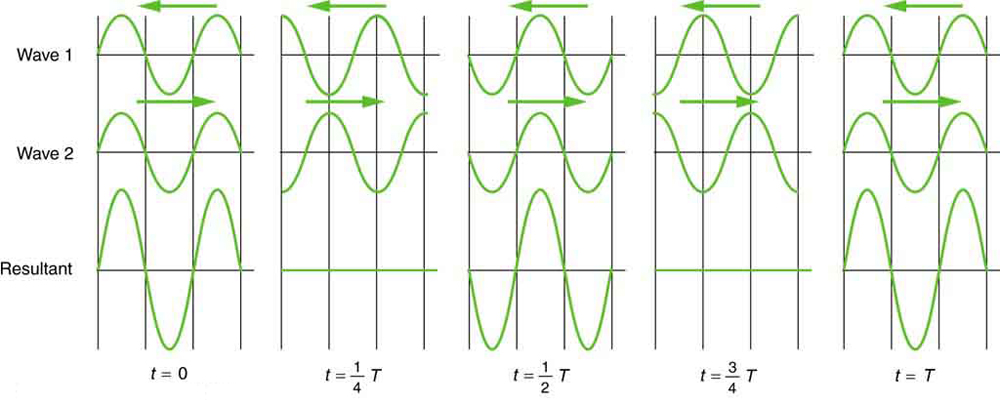
Às vezes, as ondas parecem não se mover; ao contrário, elas simplesmente vibram no mesmo lugar. Ondas imóveis podem ser vistas na superfície de um copo de leite em uma geladeira, por exemplo. As vibrações do motor do refrigerador criam ondas no leite que oscilam para cima e para baixo, mas parecem não se mover pela superfície. Essas ondas são formadas pela superposição de duas ou mais ondas em movimento, como ilustrado na Figura\(\PageIndex{5}\) para duas ondas idênticas se movendo em direções opostas. As ondas se movem umas pelas outras com seus distúrbios aumentando à medida que passam. Se as duas ondas tiverem a mesma amplitude e comprimento de onda, elas alternam entre interferência construtiva e destrutiva. A resultante parece uma onda parada e, portanto, é chamada de onda estacionária. Ondas no copo de leite são um exemplo de ondas estacionárias. Existem outras ondas estacionárias, como nas cordas de guitarra e nos tubos de órgão. Com o copo de leite, as duas ondas que produzem ondas estacionárias podem vir de reflexos na lateral do copo.

Uma análise mais detalhada dos terremotos fornece evidências de condições apropriadas para ressonância, ondas estacionárias e interferência construtiva e destrutiva. Um edifício pode ficar vibrado por vários segundos com uma frequência de condução correspondente à frequência natural de vibração do edifício, produzindo uma ressonância que resulta no colapso de um edifício, enquanto os edifícios vizinhos não. Muitas vezes, edifícios de uma certa altura são devastados, enquanto outros edifícios mais altos permanecem intactos. A altura do edifício corresponde à condição para configurar uma onda estacionária para essa altura específica. À medida que as ondas do terremoto viajam pela superfície da Terra e refletem em rochas mais densas, a interferência construtiva ocorre em certos pontos. Muitas vezes, as áreas mais próximas do epicentro não são danificadas, enquanto as áreas mais distantes são danificadas.

Combinações de ondas estacionárias de duas ondas são mostradas. No momento, t é igual a zero. As ondas estão na mesma fase, então a amplitude da onda sobreposta é o dobro da onda um e dois. Na segunda figura no tempo t é igual a um quarto do período T, as ondas estão na fase oposta, então sua figura sobreposta é uma linha reta. Novamente, no momento em que t é igual à metade do período de tempo em que as ondas estão na mesma fase e o processo é repetido em t é igual a três quartos do período de tempo e no final do período de tempo T. — Figura\(\PageIndex{5}\): Onda estacionária criada pela superposição de duas ondas idênticas se movendo em direções opostas. As oscilações estão em locais fixos no espaço e resultam de interferências alternadamente construtivas e destrutivas.

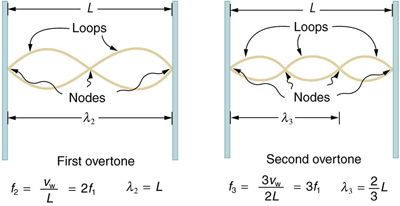
Ondas estacionárias também são encontradas nas cordas dos instrumentos musicais e são devidas aos reflexos das ondas nas pontas da corda. A figura\(\PageIndex{6}\) e a figura\(\PageIndex{7}\) mostram três ondas estacionárias que podem ser criadas em uma corda que é fixada em ambas as extremidades. Os nós são os pontos em que a corda não se move; de forma mais geral, os nós são onde a perturbação da onda é zero em uma onda estacionária. As extremidades fixas das cordas também devem ser nós, porque a corda não pode se mover para lá. A palavra antinode é usada para indicar a localização da amplitude máxima em ondas estacionárias. As ondas estacionárias nas cordas têm uma frequência relacionada à velocidade\(v_w\) de propagação da perturbação na corda. O comprimento de onda\(\lambda\) é determinado pela distância entre os pontos em que a corda está fixada no lugar.

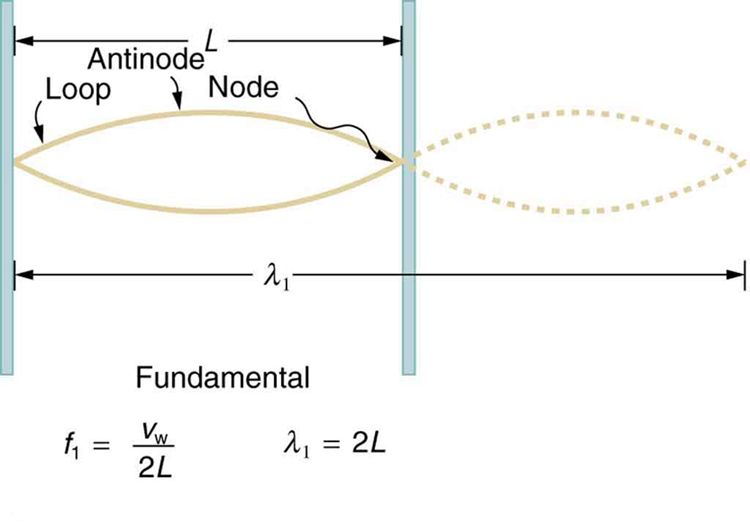
O gráfico mostra uma onda com comprimento de onda lambda um igual a L, que tem dois loops. Há três nós e dois antinodes na figura. O comprimento de um loop é L. — Figura\(\PageIndex{6}\): A figura mostra uma corda oscilando em sua frequência fundamental.

A frequência mais baixa, chamada de frequência fundamental, é, portanto, para o comprimento de onda mais longo, o que se vê\(\lambda_1 = 2L\). Portanto, a frequência fundamental é\(f_1 = v_w/\lambda_1 = v_w/2L\). Nesse caso, os sobretons ou harmônicos são múltiplos da frequência fundamental. Como visto na Figura\(\PageIndex{7}\), o primeiro harmônico pode ser facilmente calculado desde então\(\lambda_2 = L\). Assim,\(f_2 = v_w/\lambda_2 = v_w/2L = 2f_1\). Da mesma forma\(f_3 = 3f_1\), e assim por diante. Todas essas frequências podem ser alteradas ajustando a tensão na corda. Quanto maior a tensão, maior\(v_w\) é e maiores são as frequências. Essa observação é familiar para qualquer pessoa que já tenha observado um instrumento de cordas sendo afinado. Veremos nos capítulos posteriores que as ondas estacionárias são cruciais para muitos fenômenos de ressonância, como em caixas de som em instrumentos de corda.

o primeiro tom é mostrado como o comprimento da onda se lambda dois for L e houver três nós e dois antinodes na figura. Para o primeiro sobrestom, a frequência de dois é igual a duas vezes de um. — Figura\(\PageIndex{7}\): A primeira e a segunda frequências harmônicas são mostradas.

Beats

Tocar duas teclas adjacentes em um piano produz uma combinação de distorções geralmente considerada desagradável. A superposição de duas ondas de frequências semelhantes, mas não idênticas, é a culpada. Outro exemplo é frequentemente perceptível em aeronaves a jato, particularmente na variedade de dois motores, durante o taxiamento. O som combinado dos motores sobe e desce em volume. Esse volume variável ocorre porque as ondas sonoras têm frequências semelhantes, mas não idênticas. A distorção discordante do piano e a intensidade flutuante do ruído do motor a jato devem-se tanto à interferência construtiva quanto destrutiva alternada à medida que as duas ondas entram e saem de fase. A figura\(\PageIndex{8}\) ilustra isso graficamente.

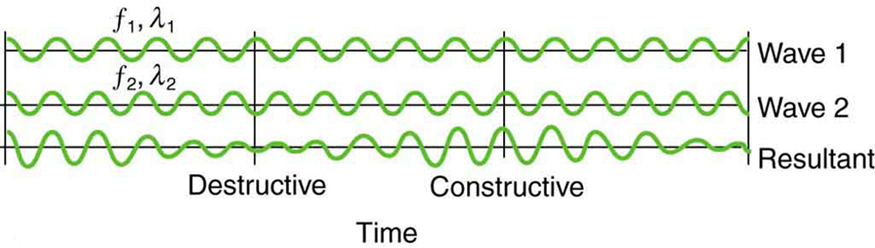
O gráfico mostra a sobreposição de duas ondas semelhantes, mas não idênticas. As batidas são produzidas alternando ondas destrutivas e construtivas com amplitude igual, mas com frequências diferentes. A onda resultante é aquela com amplitude crescente e decrescente em diferentes intervalos de tempo. — Figura\(\PageIndex{8}\): As batidas são produzidas pela superposição de duas ondas de frequências ligeiramente diferentes, mas com amplitudes idênticas. As ondas alternam no tempo entre interferência construtiva e interferência destrutiva, dando à onda resultante uma amplitude variável no tempo.

A onda resultante da superposição de duas ondas de frequência similar tem uma frequência que é a média das duas. Essa onda flutua em amplitude, ou batidas, com uma frequência chamada frequência de batida. Podemos determinar a frequência da batida adicionando duas ondas matematicamente. Observe que uma onda pode ser representada em um ponto no espaço como

\[x = X \, cos \left(\dfrac{2\pi t}{T} \right) = X \, cos \, (2\pi \, ft),\]

onde\(f = 1/T\) está a frequência da onda. Adicionar duas ondas que têm frequências diferentes, mas amplitudes idênticas, produz um resultado

\[x = x_1 + x_2.\]

Mais especificamente,

\[x = X \, cos (2\pi \, f_1 t) + X \, cos (2\pi \, f_2 t).\]

Usando uma identidade trigonométrica, pode-se mostrar que

\[x = 2X \, cos (\pi \, f_Bt) cos (2\pi \, f_{ave}t),\]

onde

\[f_B = |f_1 - f_2|\]

é a frequência da batida e\(f_{ave}\) é a média de\(f_1\)\(f_2\) e. Esses resultados significam que a onda resultante tem o dobro da amplitude e da frequência média das duas ondas sobrepostas, mas também flutua na amplitude geral na frequência de batida\(f_B\). O primeiro termo de cosseno na expressão efetivamente faz com que a amplitude suba e diminua. O segundo termo do cosseno é a onda com frequência\(f_{ave}\). Esse resultado é válido para todos os tipos de ondas. No entanto, se for uma onda sonora, desde que as duas frequências sejam semelhantes, o que ouvimos é uma frequência média que fica cada vez mais alta (ou distorções) na frequência da batida.

FAZENDO CONEXÕES DE CARREIRA

Os afinadores de piano usam batidas rotineiramente em seus trabalhos. Ao comparar uma nota com um diapasão, eles escutam as batidas e ajustam a corda até que as batidas desapareçam (até a frequência zero). Por exemplo, se o diapasão tiver uma\(256 hZ\) frequência e duas batidas por segundo forem ouvidas, a outra frequência será\(254\) ou\(258 \, Hz\). A maioria das teclas atinge várias cordas, e essas cordas são realmente ajustadas até que tenham quase a mesma frequência e forneçam uma batida lenta para maior riqueza. Guitarras e bandolins de doze cordas também são afinados usando batidas.

Embora as batidas às vezes possam ser irritantes em sons audíveis, descobriremos que as batidas têm muitas aplicações. Observar batidas é uma forma muito útil de comparar frequências semelhantes. Existem aplicações de batidas aparentemente tão díspares quanto em imagens ultrassônicas e armadilhas de velocidade por radar.

Exercício\(\PageIndex{1}\)

Imagine que você está segurando uma ponta de uma corda de pular e seu amigo segura a outra. Se sua amiga ficar parada, você pode movê-la para cima e para baixo, criando uma onda transversal. Se sua amiga começar a mover a ponta para cima e para baixo, gerando uma onda na direção oposta, quais formas de onda resultantes você esperaria ver na corda de pular?

Responda: A corda alternaria entre ter ondas com amplitudes duas vezes a amplitude original e atingir o equilíbrio sem nenhuma amplitude. Os comprimentos de onda resultarão em interferência construtiva e destrutiva.

Exercício\(\PageIndex{2}\)

Adicione texto aqui. Para que o número automático funcione, você precisa adicionar o modelo “AutoNum” (de preferência no final) à página.

Responda: Os nós são áreas de interferência de ondas onde não há movimento. Antinodes são áreas de interferência de ondas em que o movimento está em seu ponto máximo.

Exercício\(\PageIndex{3}\)

Você conecta um sistema estéreo. Ao testar o sistema, você percebe que, em um canto da sala, os sons parecem monótonos. Em outra área, os sons parecem excessivamente altos. Descreva como o som que se move pela sala pode resultar nesses efeitos.

Responda: Com vários alto-falantes emitindo sons na sala e esses sons saltando nas paredes, é provável que haja alguma interferência nas ondas. Nas áreas sombrias, a interferência provavelmente é principalmente destrutiva. Nas áreas mais altas, a interferência provavelmente é principalmente construtiva.

EXPLORAÇÕES PHET: INTERFERÊNCIA DE ONDAS

Faça ondas com uma torneira pingando, alto-falante de áudio ou laser! Adicione uma segunda fonte ou um par de fendas para criar um padrão de interferência.

Resumo

A superposição é a combinação de duas ondas no mesmo local.
A interferência construtiva ocorre quando duas ondas idênticas são sobrepostas na fase.
A interferência destrutiva ocorre quando duas ondas idênticas são sobrepostas exatamente fora de fase.
Uma onda estacionária é aquela em que duas ondas se sobrepõem para produzir uma onda que varia em amplitude, mas não se propaga.
Os nós são pontos sem movimento em ondas estacionárias.
Um antinodo é a localização da amplitude máxima de uma onda estacionária.
Ondas em uma corda são ondas estacionárias ressonantes com uma frequência fundamental e podem ocorrer em múltiplos mais altos do fundamental, chamados de sobretons ou harmônicos.
As batidas ocorrem quando ondas de frequências\(f_1\) semelhantes\(f_2\) são sobrepostas. A amplitude resultante oscila com uma frequência de batida dada por\(f_B = |f_1 - f_2|.\)

Glossário

antinodo: a localização da amplitude máxima em ondas estacionárias

frequência de batida: a frequência das flutuações de amplitude de uma onda

interferência construtiva: quando duas ondas chegam ao mesmo ponto exatamente em fase; ou seja, as cristas das duas ondas estão alinhadas com precisão, assim como as calhas

interferência destrutiva: quando duas ondas idênticas chegam ao mesmo ponto exatamente fora de fase; ou seja, alinhadas com precisão da crista à vale

frequência fundamental: a menor frequência de uma forma de onda periódica

nós: os pontos em que a corda não se move; mais geralmente, os nós são onde a perturbação da onda é zero em uma onda estacionária

conotações: múltiplos da frequência fundamental de um som

sobreposição: o fenômeno que ocorre quando duas ou mais ondas chegam ao mesmo ponto