16.9: Ondas

Last updated
Save as PDF

Page ID: 194499

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

objetivos de aprendizagem

Ao final desta seção, você poderá:

Indique as características de uma onda.
Calcule a velocidade de propagação da onda.

O que queremos dizer quando dizemos que algo é uma onda? A onda mais intuitiva e fácil de imaginar é a conhecida onda de água. Mais precisamente, uma onda é uma perturbação que se propaga ou se move do local em que foi criada. Para ondas de água, a perturbação está na superfície da água, talvez criada por uma pedra jogada em um lago ou por um nadador espirrando a superfície repetidamente. Para ondas sonoras, o distúrbio é uma mudança na pressão do ar, talvez criada pelo cone oscilante dentro de um alto-falante. Para terremotos, existem vários tipos de distúrbios, incluindo distúrbios da superfície da Terra e distúrbios de pressão sob a superfície. Até as ondas de rádio são mais facilmente compreendidas usando uma analogia com as ondas de água. A visualização das ondas da água é útil porque há mais do que apenas uma imagem mental. As ondas de água apresentam características comuns a todas as ondas, como amplitude, período, frequência e energia. Todas as características da onda podem ser descritas por um pequeno conjunto de princípios subjacentes.

Há uma onda alta de cerca de 10 pés de altura em um mar. Três barcos transportando três e quatro pessoas cada estão à frente da onda, que está vindo em sua direção. — Figura\(\PageIndex{1}\): As ondas no oceano se comportam de forma semelhante a todos os outros tipos de ondas. (crédito: Steve Jurveston, Flickr)

Uma onda é uma perturbação que se propaga ou se move do local em que foi criada. As ondas mais simples se repetem por vários ciclos e estão associadas a movimentos harmônicos simples. Vamos começar considerando a onda de água simplificada na Figura\(\PageIndex{2}\). A onda é uma perturbação da superfície da água para cima e para baixo. Isso faz com que uma gaivota marinha se mova para cima e para baixo em movimentos harmônicos simples à medida que as cristas e vales das ondas (picos e vales) passam sob o pássaro. O tempo para um movimento completo para cima e para baixo é o período da onda\(T\). A frequência da onda é\(f = 1/T\), como sempre. A onda em si se move para a direita na figura. Esse movimento da onda é, na verdade, a perturbação que se move para a direita, não a água em si (ou o pássaro se moveria para a direita). Definimos a velocidade da onda\(v_w\) como sendo a velocidade na qual a perturbação se move. Às vezes, a velocidade da onda também é chamada de velocidade de propagação ou velocidade de propagação, porque a perturbação se propaga de um local para outro.

ALERTA DE EQUÍVOC

Muitas pessoas pensam que as ondas de água empurram a água de uma direção para outra. Na verdade, as partículas de água tendem a permanecer em um local, exceto por se moverem para cima e para baixo devido à energia da onda. A energia avança pela água, mas a água permanece em um só lugar. Se você se sentir empurrado em um oceano, o que você sente é a energia da onda, não uma onda de água.

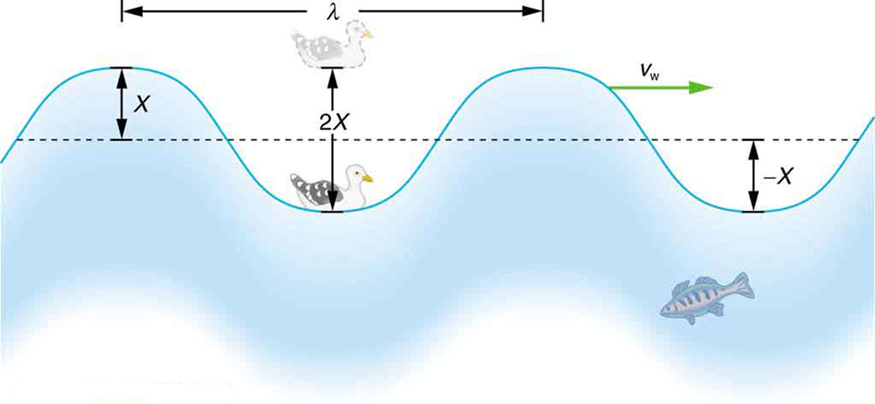
A figura mostra uma onda oceânica idealizada com duas cristas e duas calhas que passa sob uma gaivota marinha que balança para cima e para baixo em movimentos harmônicos simples. A onda tem uma lambda de comprimento de onda, que é a distância entre partes idênticas adjacentes da onda. A altura de uma crista é igual à profundidade da calha que é X, portanto, a distância vertical total entre o topo de uma crista e a parte inferior da calha é de dois X. — Figura\(\PageIndex{2}\): Uma onda oceânica idealizada passa por baixo de uma gaivota marinha que balança para cima e para baixo em simples movimento harmônico. A onda tem um comprimento de onda\(\lambda\) que é a distância entre partes idênticas adjacentes da onda. A perturbação da superfície para cima e para baixo se propaga paralelamente à superfície em uma velocidade\(v_w\).

A onda de água na Figura\(\PageIndex{2}\) também tem um comprimento associado a ela, chamado comprimento de onda\(\lambda\) de distância entre partes idênticas adjacentes de uma onda. (\(\lambda\)é a distância paralela à direção da propagação.) A velocidade de propagação\(v_w\) é a distância que a onda percorre em um determinado tempo, que é um comprimento de onda no tempo de um período. Em forma de equação, isso é

\[v_w = \dfrac{\lambda}{T} \label{eq1}\]

\[v_w = f\lambda. \label{eq2}\]

Essa relação fundamental vale para todos os tipos de ondas. Para ondas de água,\(v_w\) é a velocidade de uma onda superficial; para o som,\(v_w\) é a velocidade do som; e para a luz visível,\(v_w\) é a velocidade da luz, por exemplo.

EXPERIÊNCIA PARA LEVAR PARA CASA: ONDAS EM UMA TIGELA

Encha uma tigela grande ou bacia com água e espere que a água assente para que não haja ondulações. Coloque delicadamente uma rolha no meio da tigela. Estime o comprimento de onda e o período de oscilação da onda de água que se propaga para longe da cortiça. Retire a rolha da tigela e espere a água repousar novamente. Solte suavemente a rolha a uma altura diferente da primeira gota. O comprimento de onda depende de quão acima da água a cortiça cai?

Exemplo\(\PageIndex{1}\): Calculate the Velocity of Wave Propagation: Gull in the Ocean

Calcule a velocidade da onda do oceano na Figura\(\PageIndex{2}\) se a distância entre as cristas das ondas for 10,0 m e o tempo para uma gaivota subir e descer for 5,00 s.

Estratégia

Somos convidados a encontrar\(v_w\). As informações fornecidas nos dizem que\(\lambda = 10.0 \, m\)\(T = 5.00 \, s\) e. Portanto, podemos usar a Equação\ ref {eq1} para encontrar a velocidade da onda.

Solução

Insira os valores conhecidos na Equação\ ref {eq1}:\[\begin{align*} v_w &= \frac{\lambda}{T} \\[5pt] &= \dfrac{10.0 \, m}{5.00 \, s}. \end{align*}\]
Resolva\(v_w\) para encontrar\(v_w = 2.00 \, m/s.\)

Discussão

Essa velocidade lenta parece razoável para uma onda oceânica. Observe que a onda se move para a direita na figura nessa velocidade, não na velocidade variável com que a gaivota se move para cima e para baixo.

Ondas transversais e longitudinais

Uma onda simples consiste em uma perturbação periódica que se propaga de um lugar para outro. A onda na Figura\(\PageIndex{3}\) se propaga na direção horizontal enquanto a superfície é perturbada na direção vertical. Essa onda é chamada de onda transversal ou onda de cisalhamento; em tal onda, a perturbação é perpendicular à direção da propagação. Em contraste, em uma onda longitudinal ou onda compressional, a perturbação é paralela à direção da propagação. A figura\(\PageIndex{4}\) mostra um exemplo de uma onda longitudinal. O tamanho da perturbação é sua amplitude X e é completamente independente da velocidade de propagação\(v_w\).

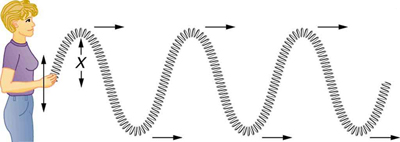
A figura mostra uma mulher segurando uma longa mola na mão e movendo-a para cima e para baixo, fazendo com que ela se afaste dela em ziguezague. É um exemplo de onda transversal, a onda se propaga horizontalmente. A direção do movimento da onda é mostrada com a ajuda das setas direitas em cada crista e vale. — Figura\(\PageIndex{3}\): Neste exemplo de onda transversal, a onda se propaga horizontalmente e a perturbação no cordão está na direção vertical.

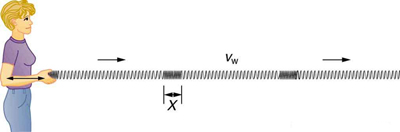
A figura mostra uma mulher em pé à esquerda empurrando uma longa mola para dentro e para trás em movimento horizontal, longe dela, sem mover a mão para cima e para baixo. O cordão se estica e se contrai para frente e para trás. Este é um exemplo de onda longitudinal, a onda se propaga horizontalmente. Em alguns pontos, a mola é comprimida e em outros pontos a mola é expandida. Uma peça contraída é igual à amplitude X. — Figura\(\PageIndex{4}\): Neste exemplo de onda longitudinal, a onda se propaga horizontalmente e a perturbação no cordão também está na direção horizontal.

As ondas podem ser transversais, longitudinais ou uma combinação das duas. (As ondas de água são na verdade uma combinação de transversais e longitudinais. A onda de água simplificada ilustrada na Figura não\(\PageIndex{2}\) mostra nenhum movimento longitudinal da ave.) As ondas nas cordas dos instrumentos musicais são transversais, assim como as ondas eletromagnéticas, como a luz visível.

As ondas sonoras no ar e na água são longitudinais. Seus distúrbios são variações periódicas na pressão que são transmitidas nos fluidos. Os fluidos não têm resistência ao cisalhamento apreciável e, portanto, as ondas sonoras neles devem ser longitudinais ou compressionais. O som em sólidos pode ser longitudinal e transversal.

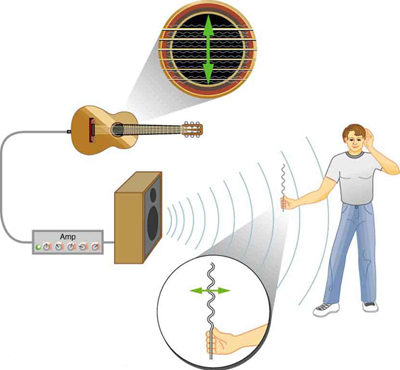
A figura mostra uma guitarra conectada a um amplificador e um homem segurando uma folha de papel voltada para o alto-falante conectado ao amplificador. As cordas do violão quando tocadas causam ondas transversais. Por outro lado, o som do violão cria ondulações na folha de papel, fazendo com que ela trema em uma direção que mostra que as ondas sonoras são longitudinais. — Figura\(\PageIndex{5}\): A onda em uma corda de violão é transversal. A onda sonora sacude uma folha de papel em uma direção que mostra que a onda sonora é longitudinal.

As ondas de terremoto sob a superfície da Terra também têm componentes longitudinais e transversais (chamadas de ondas compressionais ou P e ondas de cisalhamento ou S, respectivamente). Esses componentes têm características individuais importantes — eles se propagam em velocidades diferentes, por exemplo. Os terremotos também têm ondas superficiais semelhantes às ondas superficiais na água.

Exercício\(\PageIndex{1}\):Check Your Understanding

Por que é importante diferenciar entre ondas longitudinais e transversais?

Resposta: Nos diferentes tipos de ondas, a energia pode se propagar em uma direção diferente em relação ao movimento da onda. Isso é importante para entender como os diferentes tipos de ondas afetam os materiais ao seu redor.

EXPLORAÇÕES DE PHET: ONDA EM UMA CORDA

Veja uma corda vibrar em câmera lenta com esta simulação PhET. Mexa a ponta da corda e faça ondas, ou ajuste a frequência e a amplitude de um oscilador. Ajuste o amortecimento e a tensão. A extremidade pode ser fixa, solta ou aberta.

Resumo

Uma onda é uma perturbação que se move do ponto de criação com uma velocidade de onda\(v_w\).
Uma onda tem um comprimento de onda\(\lambda\) que é a distância entre partes idênticas adjacentes da onda.
A velocidade e o comprimento de onda estão relacionados à frequência e ao período da onda por\(v_w = \frac{\lambda}{T}\) ou\(v_w = f\lambda\).
Uma onda transversal tem uma perturbação perpendicular à sua direção de propagação, enquanto uma onda longitudinal tem uma perturbação paralela à sua direção de propagação.

Glossário

onda longitudinal: uma onda na qual a perturbação é paralela à direção da propagação

onda transversal: uma onda na qual a perturbação é perpendicular à direção da propagação

velocidade de onda: a velocidade com que a perturbação se move. Também chamada de velocidade de propagação ou velocidade de propagação

Comprimento de onda: a distância entre partes idênticas adjacentes de uma onda