16.7: Movimento harmônico amortecido

Last updated
Save as PDF

Page ID: 194486

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Compare e discuta sistemas oscilantes com amortecimento insuficiente e sobreamortecido.
Explique o sistema criticamente amortecido.

Uma corda de guitarra para de oscilar alguns segundos depois de ser dedilhada. Para manter uma criança feliz em um balanço, você deve continuar empurrando. Embora muitas vezes possamos tornar o atrito e outras forças não conservadoras insignificantemente pequenos, movimentos completamente sem amortecimento são raros. Na verdade, podemos até querer amortecer as oscilações, como nos amortecedores de carros.

Na figura mostrada, uma criança pequena está sentada em um balanço de mola, amarrada com um cinto na cintura. Na parte de trás está seu pai, que está empurrando o balanço no movimento de ida e volta. — Figura\(\PageIndex{1}\): Para neutralizar as forças de amortecimento, esse pai precisa continuar pressionando o balanço. (crédito: Erik A. Johnson, Flickr)

Para um sistema que tem uma pequena quantidade de amortecimento, o período e a frequência são quase os mesmos do movimento harmônico simples, mas a amplitude diminui gradualmente, conforme mostrado na Figura\(\PageIndex{2}\). Isso ocorre porque a força de amortecimento não conservadora remove energia do sistema, geralmente na forma de energia térmica. Em geral, a remoção de energia por forças não conservadoras é descrita como\[W_{nc} = \Delta (KE + PE),\] onde o trabalho\(W_{nc}\) é realizado por uma força não conservadora (aqui a força de amortecimento). Para um oscilador harmônico amortecido,\(W_{nc}\) é negativo porque remove a energia mecânica (KE + PE) do sistema.

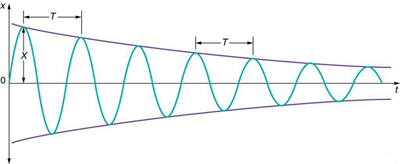
A figura mostra um gráfico do deslocamento, ao longo do eixo y, versus o tempo de um oscilador harmônico, percorrendo o eixo x, igualmente em quadrantes positivos e negativos. A amplitude, X, das oscilações é mostrada por uma onda verde que está diminuindo gradualmente à medida que nos afastamos do eixo y, mas o tempo, T, mostrado aqui como a distância entre cristas adjacentes permanece o mesmo por toda parte. — Figura\(\PageIndex{2}\): Neste gráfico de deslocamento versus tempo para um oscilador harmônico com uma pequena quantidade de amortecimento, a amplitude diminui lentamente, mas o período e a frequência são quase os mesmos como se o sistema estivesse completamente sem amortecimento.

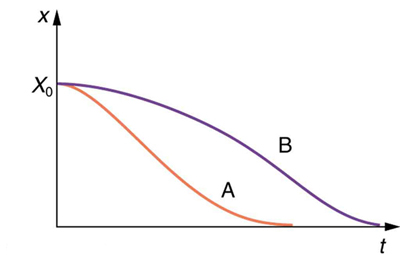
Se você aumentar gradualmente a quantidade de amortecimento em um sistema, o período e a frequência começarão a ser afetados, pois o amortecimento se opõe e, portanto, retarda o movimento de ida e volta. (A força líquida é menor em ambas as direções.) Se houver um amortecimento muito grande, o sistema nem oscila — ele se move lentamente em direção ao equilíbrio. A figura\(\PageIndex{3}\) mostra o deslocamento de um oscilador harmônico para diferentes quantidades de amortecimento. Quando queremos amortecer as oscilações, como na suspensão de um carro, podemos querer que o sistema retorne ao equilíbrio o mais rápido possível. O amortecimento crítico é definido como a condição na qual o amortecimento de um oscilador faz com que ele retorne o mais rápido possível ao seu posição de equilíbrio O sistema criticamente amortecido pode ultrapassar a posição de equilíbrio, mas se isso acontecer, fará isso apenas uma vez. O amortecimento crítico é representado pela curva A na Figura\(\PageIndex{3}\). Com um amortecimento menos do que crítico, o sistema retornará ao equilíbrio mais rapidamente, mas ultrapassará e cruzará uma ou mais vezes. Esse sistema está subamortecido; seu deslocamento é representado pela curva na Figura\(\PageIndex{2}\). A curva B na Figura\(\PageIndex{3}\) representa um sistema sobreamortecido. Assim como no amortecimento crítico, ele também pode ultrapassar a posição de equilíbrio, mas alcançará o equilíbrio por um longo período de tempo.

O gráfico fornecido é de deslocamento, ao longo do eixo y, versus tempo ao longo do eixo x. O símbolo para deslocamento é dado como X subscrito zero e para o tempo é dado como t. Duas curvas começam em um ponto ao longo do eixo y, onde X subscrito zero é maior que zero. A curva A é curvada para baixo e encontra o eixo x em um ponto. A curva B é curva para cima e está sobre a curva A e encontra o eixo x em um ponto que está na extremidade direita do ponto de encontro da curva A e do eixo x. — Figura\(\PageIndex{3}\): Deslocamento versus tempo para um oscilador harmônico com amortecimento crítico (A) e um oscilador harmônico com amortecimento excessivo (B). O oscilador criticamente amortecido retorna ao equilíbrio\(X = 0\) no menor tempo possível sem ultrapassar.

O amortecimento crítico é frequentemente desejado, porque esse sistema retorna ao equilíbrio rapidamente e também permanece em equilíbrio. Além disso, uma força constante aplicada a um sistema criticamente amortecido move o sistema para uma nova posição de equilíbrio no menor tempo possível, sem ultrapassar ou oscilar em torno da nova posição. Por exemplo, quando você está em balanças de banheiro que têm um medidor de agulha, a agulha se move para sua posição de equilíbrio sem oscilar. Seria muito inconveniente se a agulha oscilasse em torno da nova posição de equilíbrio por um longo tempo antes de se estabilizar. As forças de amortecimento podem variar muito em caráter. O atrito, por exemplo, às vezes é independente da velocidade (como assumido na maioria dos lugares neste texto). Mas muitas forças de amortecimento dependem da velocidade — às vezes de formas complexas, às vezes simplesmente sendo proporcionais à velocidade.

Exemplo\(\PageIndex{1}\): Damping an Oscillatory Motion: Friction on an Object Connected to a Spring

O amortecimento do movimento oscilatório é importante em muitos sistemas, e a capacidade de controlar o amortecimento é ainda mais importante. Isso geralmente é obtido usando forças não conservadoras, como atrito entre superfícies e viscosidade para objetos que se movem através de fluidos. O exemplo a seguir considera o atrito. Suponha que um objeto de 0,200 kg esteja conectado a uma mola\(\PageIndex{4}\), conforme mostrado na Figura, mas há atrito simples entre o objeto e a superfície, e o coeficiente de atrito\(\mu_k\) é igual a 0,0800. (a) Qual é a força de atrito entre as superfícies? (b) Qual a distância total que o objeto percorre se for liberado a 0,100 m do equilíbrio, começando em\(v = 0\)? A constante de força da mola é\(k = 50.0 \, N/m\).

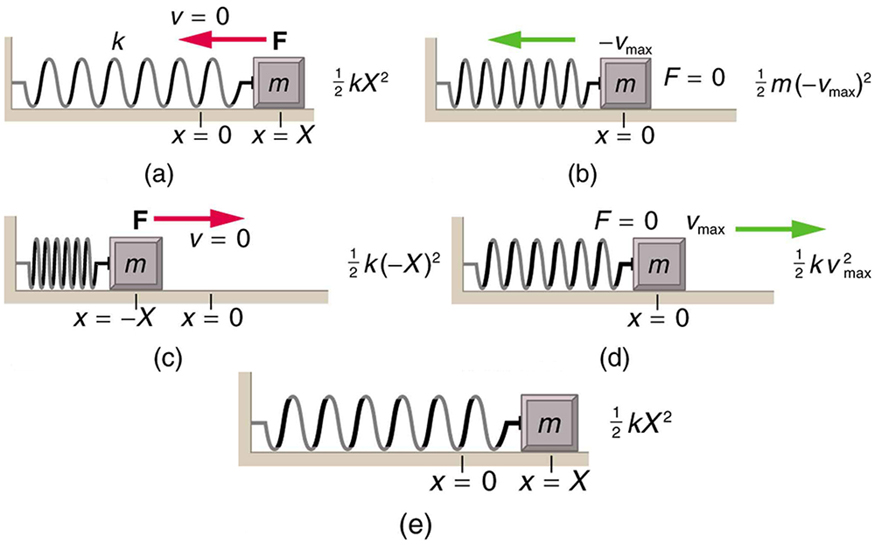
A figura dada (a) mostra uma mola em uma superfície sem atrito presa a uma barra ou parede do lado esquerdo e no lado direito da mola, há um objeto preso com massa m. Sua amplitude é dada por X e X é igual a zero no nível de equilíbrio. A força F é aplicada a ela do lado direito, representada por uma seta vermelha apontando para a esquerda e a velocidade v é igual a zero. Uma seta mostrando a direção da força também é dada ao lado desta figura, bem como com as outras quatro figuras. A energia do objeto é meio k x ao quadrado. Na figura dada (b), após a aplicação da força, o objeto se move para a esquerda, comprimindo levemente a mola. O deslocamento do objeto de sua posição inicial é indicado por pontos. A força F, aqui é igual a zero e a velocidade v, é máxima na direção negativa ou na esquerda. A energia do objeto nesse caso é meio m vezes menos v-max ao quadrado inteiro. Na figura dada (c), a mola foi comprimida com o limite máximo e a amplitude é menos X. Agora, a força está voltada para a direita, indicada aqui com uma seta vermelha apontando para a direita e a velocidade, v, é zero. A energia do objeto agora é meio k vezes menos x quadrado inteiro. Na figura dada (d), a mola é mostrada liberada de sua posição comprimida e o objeto se move em direção ao lado direito para atingir o nível de equilíbrio. Aqui, F é igual a zero e a velocidade, v, é a máxima. A energia do objeto se torna meio k vezes v máximo ao quadrado. Na figura dada (e), a mola foi esticada até o limite máximo possível e o objeto foi movido para a extrema direita. Agora, a velocidade v, aqui, é igual a zero e a direção da força está voltada para a esquerda. Como mostrado aqui, F é igual a zero. A energia do objeto nesse caso é meio k vezes x ao quadrado. — Figura\(\PageIndex{4}\): A transformação da energia em movimento harmônico simples é ilustrada para um objeto preso a uma mola em uma superfície sem atrito.

Estratégia

Esse problema exige que você integre seu conhecimento de vários conceitos sobre ondas, oscilações e amortecimento. Para resolver um problema de conceito integrado, você deve primeiro identificar os princípios físicos envolvidos. A parte (a) é sobre a força de atrito. Este é um tópico que envolve a aplicação das Leis de Newton. A parte (b) requer uma compreensão do trabalho e da conservação de energia, bem como alguma compreensão dos sistemas oscilatórios horizontais.

Agora que identificamos os princípios que devemos aplicar para resolver os problemas, precisamos identificar os conhecidos e desconhecidos para cada parte da pergunta, bem como a quantidade que é constante na Parte (a) e na Parte (b) da pergunta.

Solução a

Escolha a equação adequada: O atrito é\(f = \mu_kmg\).
Identifique os valores conhecidos.
Insira os valores conhecidos na equação:\[f = (0.0800)(0.200 \, kg)(9.80 \, m/s^2).\]
Calcule e converta unidades:\(f = 0.157 \, N\).

Discussão em

A força aqui é pequena porque o sistema e os coeficientes são pequenos.

Solução b

Identifique o conhecido:

O sistema envolve energia potencial elástica à medida que a mola se comprime e se expande, atrito relacionado ao trabalho realizado e energia cinética à medida que o corpo acelera e desacelera.
A energia não é conservada à medida que a massa oscila porque o atrito é uma força não conservadora.
O movimento é horizontal, então a energia potencial gravitacional não precisa ser considerada.
Como o movimento começa do repouso, a energia no sistema é inicial\(PE_{el,i} = (1/2)kX^2\). Essa energia é removida pelo trabalho realizado por atrito\(W_{nc} = -fd\), onde\(d\) é a distância total percorrida e\(f = \mu_kmg\) é a força do atrito. Quando o sistema para de se mover, a força de atrito equilibra a força exercida pela mola, então\(PE_{el,f} = (1/2)kx^2\), onde\(x\) está a posição final e é dada por\[F_{el} = f\]\[kx = \mu_kmg.\]\[x = \dfrac{\mu_kmg}{k}\]

Ao igualar o trabalho realizado à energia removida, resolva a distância\(d\).
O trabalho realizado pelas forças não conservadoras é igual à energia potencial elástica inicial armazenada. Identifique a equação correta a ser usada:\[W_{nc} = \Delta (KE + PE) = PE_{el,f} - PE_{el,i} = \dfrac{1}{2}k \left(\left(\dfrac{\mu_kmg}{k}\right)^2 - X^2\right).\]
Lembre-se disso\(W_{nc} = -fd\).
Insira o atrito como\(f = \mu_kmg\) em\(W_{nc} = - fd\), assim\[W_{nc} = \mu_kmgd.\]
Combine essas duas equações para encontrar\[\dfrac{1}{2}k \left( \left(\dfrac{\mu_kmg}{k}\right)^2 - X^2\right) = - \mu_kmgd.\]
Resolva a equação para\(d\):\[d = \dfrac{k}{2\mu_kmg} \left(X^2 - \left(\dfrac{\mu_kmg}{k}\right)^2\right).\]
Insira os valores conhecidos na equação resultante:\[d = \dfrac{50.0 \, N/m}{2(0.0800)(0.200 \, kg)(9.80 \, m/s^2)}\left((0.100 \, m)^2 - \left(\dfrac{(0.0800)(0.200 \, kg)(9.80 \, m/s^2)}{50.0 \, N/m} \right)^2 \right).\]
\(d\)Calcule e converta unidades:\[d = 1.59 \, m\]

Discussão b

Essa é a distância total percorrida para frente e para trás\(x = 0\), que é a posição de equilíbrio sem amortecimento. O número de oscilações em torno da posição de equilíbrio será maior do que\(d/X = (1.59 \, m)(0.100 \, m) = 15.9\) porque a amplitude das oscilações está diminuindo com o tempo. Ao final do movimento, esse sistema não retornará\(x = 0\) para esse tipo de força de amortecimento, pois o atrito estático excederá a força de restauração. Este sistema está pouco amortecido. Em contraste, um sistema sobreamortecido com uma simples força de amortecimento constante não cruzaria a posição de equilíbrio\(x = 0\) uma única vez. Por exemplo, se esse sistema tivesse uma força de amortecimento 20 vezes maior, ele se moveria apenas 0,0484 m em direção à posição de equilíbrio a partir de sua posição original de 0,100 m.

Este exemplo prático ilustra como aplicar estratégias de resolução de problemas a situações que integram os diferentes conceitos que você aprendeu. O primeiro passo é identificar os princípios físicos envolvidos no problema. O segundo passo é resolver as incógnitas usando estratégias familiares de resolução de problemas. Eles são encontrados em todo o texto, e muitos exemplos úteis mostram como usá-los para tópicos individuais. Neste exemplo de conceitos integrados, você pode ver como aplicá-los em vários tópicos. Você achará essas técnicas úteis em aplicações da física fora de um curso de física, como em sua profissão, em outras disciplinas científicas e na vida cotidiana.

Exercício\(\PageIndex{1}\):Check Your Understanding

Por que osciladores harmônicos completamente sem amortecimento são tão raros?

Responda: O atrito geralmente entra em ação sempre que um objeto está se movendo. O atrito causa amortecimento em um oscilador harmônico.

Exercício\(\PageIndex{2}\):Check Your Understanding

Descreva a diferença entre sobreamortecimento, subamortecimento e amortecimento crítico.

Responda: Um sistema superamortecido se move lentamente em direção ao equilíbrio. Um sistema pouco amortecido se move rapidamente para o equilíbrio, mas oscilará em torno do ponto de equilíbrio à medida que o faz. Um sistema criticamente amortecido se move o mais rápido possível em direção ao equilíbrio sem oscilar em torno do equilíbrio.

Resumo

Os osciladores harmônicos amortecidos têm forças não conservadoras que dissipam sua energia.
O amortecimento crítico devolve o sistema ao equilíbrio o mais rápido possível, sem ultrapassagem.
Um sistema com amortecimento insuficiente oscilará na posição de equilíbrio.
Um sistema com amortecimento excessivo se move mais lentamente em direção ao equilíbrio do que um sistema criticamente amortecido.

Glossário

amortecimento crítico: a condição na qual o amortecimento de um oscilador faz com que ele retorne o mais rápido possível à sua posição de equilíbrio sem oscilar para frente e para trás em torno dessa posição

amortecimento excessivo: a condição na qual o amortecimento de um oscilador faz com que ele retorne ao equilíbrio sem oscilar; o oscilador se move mais lentamente em direção ao equilíbrio do que no sistema criticamente amortecido

sob amortecimento: a condição na qual o amortecimento de um oscilador faz com que ele retorne ao equilíbrio com a amplitude diminuindo gradualmente para zero; o sistema retorna ao equilíbrio mais rapidamente, mas ultrapassa e cruza a posição de equilíbrio uma ou mais vezes