Skip to main content
Global

16.6: Movimento circular uniforme e movimento harmônico simples

  1. Last updated
  2. Save as PDF
  • Page ID
    194439

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Compare o movimento harmônico simples com o movimento circular uniforme.
    A figura mostra um carrossel vazio girando no sentido horário com barras de ferro segurando as estátuas de cavalos de madeira decoradas, quatro em cada coluna.
    Figura\(\PageIndex{1}\): Os cavalos deste carrossel exibem movimentos circulares uniformes. (crédito: Wonderlane, Flickr)

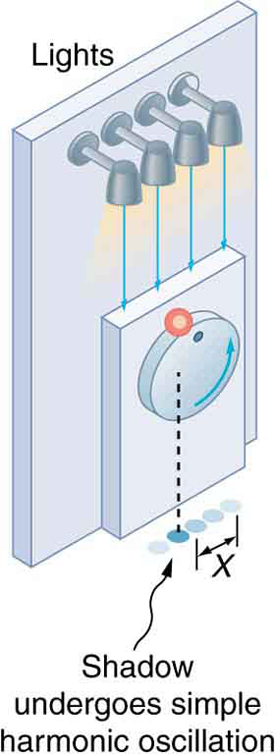
    Existe uma maneira fácil de produzir movimentos harmônicos simples usando movimentos circulares uniformes. A figura\(\PageIndex{2}\) mostra uma maneira de usar esse método. Uma bola é presa a uma mesa giratória vertical com rotação uniforme e sua sombra é projetada no chão, conforme mostrado. A sombra sofre movimentos harmônicos simples. A lei de Hooke geralmente descreve movimentos circulares uniformes (\(\omega\)constantes) em vez de sistemas que têm grandes deslocamentos visíveis. Portanto, observar a projeção de movimento circular uniforme, como na Figura\(\PageIndex{2}\), geralmente é mais fácil do que observar um oscilador harmônico simples preciso em grande escala. Se estudado com profundidade suficiente, o movimento harmônico simples produzido dessa maneira pode fornecer uma visão considerável de muitos aspectos das oscilações e ondas e é muito útil matematicamente. Em nosso breve tratamento, indicaremos algumas das principais características desse relacionamento e como elas podem ser úteis.

    A figura apresentada mostra uma mesa giratória vertical com quatro lâmpadas projetadas no piso superior. Uma barra retangular de tamanho menor é fixada a essa mesa giratória na metade inferior, com um botão circular preso a ela. Uma pequena bola vermelha está rolando ao longo do limite desse botão na direção angular, e as luzes que caem por essa bola são bolas criando sombras logo abaixo da maçaneta no chão. A sombra do meio é a mais brilhante e começa a desaparecer quando olhamos para a sombra encurralada.
    Figura\(\PageIndex{2}\): A sombra de uma bola girando em velocidade angular constante\(\omega\) em uma mesa giratória vai e volta em movimentos harmônicos simples e precisos.

    A figura\(\PageIndex{3}\) mostra a relação básica entre movimento circular uniforme e movimento harmônico simples. O ponto P percorre o círculo em uma velocidade angular constante\(\omega\). O ponto P é análogo a um objeto no carrossel. A projeção da posição de P em um eixo fixo sofre um movimento harmônico simples e é análoga à sombra do objeto. No momento mostrado na figura, a projeção tem posição\(x\) e se move para a esquerda com velocidade\(v\). A velocidade do ponto P ao redor do círculo é igual\(\bar{v}_{max}\). A projeção de\(\bar{v}_{max}\) no\(x\) eixo -é a velocidade\(v\) do movimento harmônico simples ao longo do\(x\) eixo -.

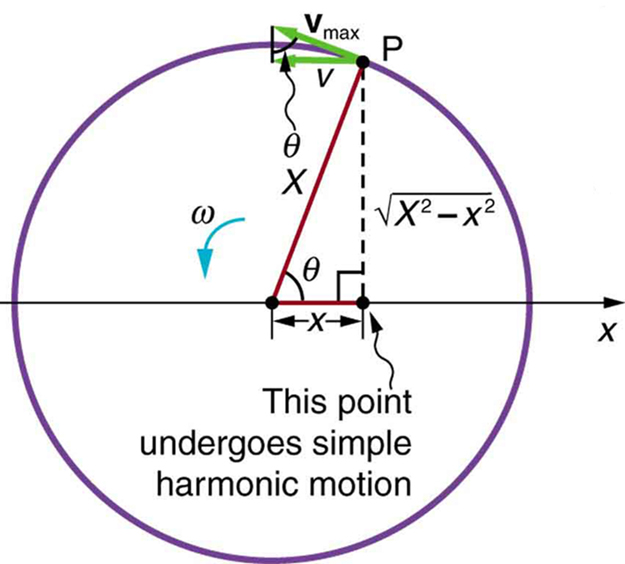
    A figura mostra um ponto P se movendo pela circunferência de um círculo de forma angular com velocidade angular ômega. O diâmetro é projetado ao longo do eixo x, com o ponto P fazendo um ângulo teta no centro do círculo. Um ponto ao longo do diâmetro mostra a projeção do ponto P com uma linha perpendicular pontilhada de P até este ponto, a projeção do ponto é dada como v ao longo do círculo e sua velocidade v subscrito max, sobre a parte superior da seta de projeção em uma direção ascendente à esquerda.
    Figura\(\PageIndex{3}\): Um ponto P se movendo em um caminho circular com uma velocidade angular constante\(\omega\) está passando por um movimento circular uniforme. Sua projeção no eixo x sofre um movimento harmônico simples. Também é mostrada a velocidade desse ponto ao redor do círculo,\(\bar{v}_{max}\), e sua projeção, que é\(v\). Observe que essas velocidades formam um triângulo semelhante ao triângulo de deslocamento.

    Para ver se a projeção sofre um movimento harmônico simples, observe que sua posição\(x\) é dada por:

    \[x = X \cos{\theta},\]

    é a velocidade angular constante e\(X\) é o raio do caminho circular. Assim,

    \[x = X \cos{\omega t}.\]

    A velocidade angular\(\omega\) está em radianos por unidade de tempo; neste caso,\(2 \pi\) radianos é o tempo para uma revolução\(T\). Isso é,\(\omega = 2\pi/T\). Substituindo essa expressão por\(\omega\), vemos que a posição\(x\) é dada por:

    \[x(t) = \cos{\left(\frac{2\pi t}{T}\right)}.\]

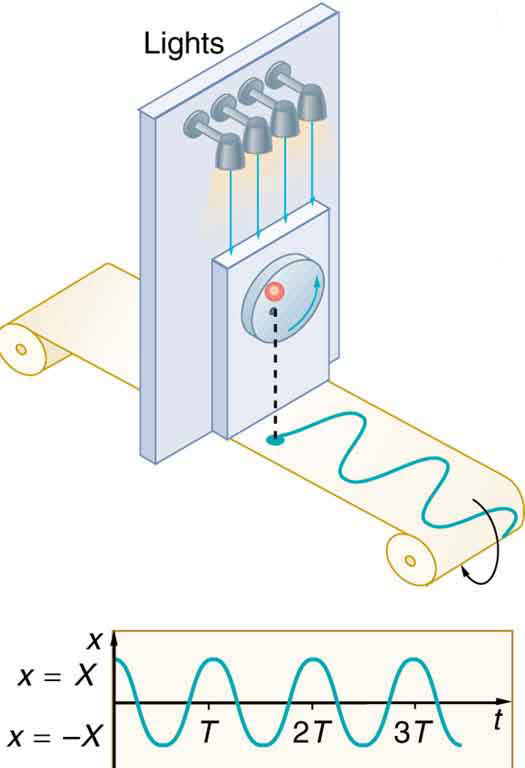
    Essa expressão é a mesma que tínhamos para a posição de um oscilador harmônico simples em Movimento harmônico simples: um movimento periódico especial. Se fizermos um gráfico da posição versus tempo, como na Figura,\(\PageIndex{4}\) veremos novamente o caráter ondulatório (típico do movimento harmônico simples) da projeção do movimento circular uniforme no\(x\) eixo.

    A figura apresentada mostra uma mesa giratória vertical com quatro lâmpadas projetadas no piso superior. Uma barra retangular de tamanho menor é fixada a essa mesa giratória na metade inferior, com um botão circular preso a ela. Uma pequena bola vermelha está rolando ao longo do limite desse botão na direção angular. A mesa giratória é colocada sobre uma folha de papel em rolo, na qual o movimento harmônico simples é medido, o que é mostrado aqui em ondas oscilantes na folha de papel em frente à mesa. Um gráfico de amplitude versus tempo também é fornecido ao lado da figura.
    Figura\(\PageIndex{4}\): A posição da projeção do movimento circular uniforme executa um movimento harmônico simples, como\(t\) indica este gráfico ondulatório de\(x\) versus.

    Agora, vamos usar\(\PageIndex{3}\) a Figura para fazer uma análise mais aprofundada do movimento circular uniforme no que se refere ao movimento harmônico simples. O triângulo formado pelas velocidades na figura e o triângulo formado pelos deslocamentos (\(X\),\(x\), e\(\sqrt{X^{2} - x^{2}}\)) são triângulos retos semelhantes. Tomando proporções de lados semelhantes, vemos que

    \[\frac{v}{v_{max}} = \frac{\sqrt{X^{X} - x^{2}}}{X} = \sqrt{1-\frac{x^{2}}{X^{2}}}.\]

    Podemos resolver essa equação para a velocidade\(v\) ou

    \[v = v_{max}\sqrt{1 - \frac{x^2}{X^{2}}}.\]

    Essa expressão para a velocidade de um oscilador harmônico simples é exatamente a mesma que a equação obtida a partir de considerações de conservação de energia em Energia e no Oscilador Harmônico Simples. Você pode começar a ver que é possível obter todas as características do movimento harmônico simples a partir de uma análise da projeção do movimento circular uniforme.

    Finalmente, vamos considerar o período\(T\) do movimento da projeção. Esse período é o tempo que o ponto P leva para completar uma revolução. Esse tempo é a circunferência da circunferência\(2 \pi X\) dividida pela velocidade ao redor da circunferência,\(v_{max}\). Assim, o período\(T\) é

    \[T = \frac{2\pi X}{v_{max}}.\]

    Sabemos, por considerações de conservação de energia, que

    \[v_{max} = \sqrt{\frac{k}{m}}X.\]

    Resolvendo essa equação para\(X/v_{max}\) dados

    \[\frac{X}{v_max} = \sqrt{\frac{m}{k}}.\]

    Substituindo essa expressão na equação por\(T\) rendimentos

    \[tT = 2\pi \sqrt{\frac{m}{k}}.\]

    Assim, o período do movimento é o mesmo de um oscilador harmônico simples. Determinamos o período para qualquer oscilador harmônico simples usando a relação entre movimento circular uniforme e movimento harmônico simples.

    Alguns módulos ocasionalmente se referem à conexão entre movimento circular uniforme e movimento harmônico simples. Além disso, se você levar seu estudo da física e suas aplicações a maiores profundidades, achará essa relação útil. Isso pode, por exemplo, ajudar a analisar como as ondas se somam quando são sobrepostas.

    Exercício\(\PageIndex{1}\)

    Identifique um objeto que sofre um movimento circular uniforme. Descreva como você pode traçar o movimento harmônico simples desse objeto como uma onda.

    Resposta

    Um toca-discos passa por um movimento circular uniforme. Você pode fixar a haste em um ponto na borda externa da mesa giratória e colocar uma caneta na outra extremidade da cavilha. Quando o toca-discos gira, a caneta se move. Você pode arrastar um pedaço de papel longo para baixo da caneta, capturando seu movimento como uma onda.

    Resumo

    • Uma projeção de movimento circular uniforme sofre uma simples oscilação harmônica.