Skip to main content
Global

16.5: Energia e o oscilador harmônico simples

  1. Last updated
  2. Save as PDF
  • Page ID
    194449

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Determine a velocidade máxima de um sistema oscilante.

    Para estudar a energia de um oscilador harmônico simples, primeiro consideramos todas as formas de energia que ele pode ter. Sabemos pela Lei de Hooke: Stress and Strain Revisited que a energia armazenada na deformação de um oscilador harmônico simples é uma forma de energia potencial dada por:

    \[PR_{el} = \dfrac{1}{2}kx^2.\]

    Como um oscilador harmônico simples não tem forças dissipativas, a outra forma importante de energia é a energia cinética\(KE\). A conservação de energia para essas duas formas é:

    \[KE + PE_{el} = constant\]

    ou

    \[\dfrac{1}{2}mv^2 + \dfrac{1}{2}kx^2 = constant.\]

    Essa declaração de conservação de energia é válida para todos os osciladores harmônicos simples, incluindo aqueles em que a força gravitacional desempenha um papel.

    Ou seja, para um pêndulo simples, substituímos a velocidade por\(v = L\omega\), a constante da mola por\(k = mg/L\) e o termo de deslocamento por\(x = L\theta\). Assim

    \[\dfrac{1}{2}mL^2\omega^2 + \dfrac{1}{2}mgL\theta^2 = constant.\]

    No caso de movimento harmônico simples sem amortecimento, a energia oscila para frente e para trás entre a cinética e o potencial, indo completamente de um para o outro à medida que o sistema oscila. Portanto, para o exemplo simples de um objeto em uma superfície sem atrito presa a uma mola, conforme mostrado novamente na Figura\(\PageIndex{1}\), o movimento começa com toda a energia armazenada na mola. Quando o objeto começa a se mover, a energia potencial elástica é convertida em energia cinética, tornando-se energia inteiramente cinética na posição de equilíbrio. Em seguida, é convertida novamente em energia potencial elástica pela mola, a velocidade se torna zero quando a energia cinética é completamente convertida e assim por diante. Esse conceito fornece uma visão extra aqui e em aplicações posteriores de movimento harmônico simples, como circuitos de corrente alternada.

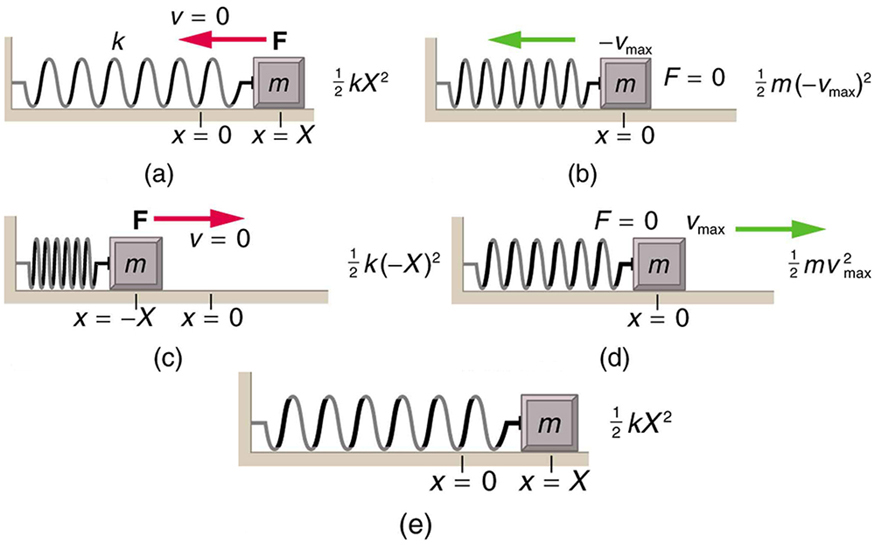
    A Figura a mostra uma mola em uma superfície sem atrito presa a uma barra ou parede do lado esquerdo, e no lado direito dela há um objeto preso a ela com massa m, sua amplitude é dada por X e x igual a zero no nível de equilíbrio. A força F é aplicada a ela do lado direito, mostrada com a seta vermelha apontada para a esquerda e a velocidade v é igual a zero. Um ponto de direção mostrando a direção norte e oeste também é fornecido ao lado desta figura, bem como com outras quatro figuras. A energia fornecida aqui para o objeto é dada de acordo com a velocidade. Na figura b, após a aplicação da força, o objeto se move para a esquerda comprimindo um pouco a mola, e a área deslocada do objeto a partir de seu ponto inicial é mostrada em pontos esboçados. F é igual a zero e V é máximo na direção negativa. A energia fornecida aqui para o objeto é dada de acordo com a velocidade. Na figura c, a mola foi comprimida até o nível máximo e a amplitude é negativa x. Agora, a direção da força muda para a direção direita, mostrada com a seta vermelha apontada para a direita e a velocidade v zero. A energia fornecida aqui para o objeto é dada de acordo com a velocidade. Na figura d, a mola é mostrada liberada do nível comprimido e o objeto se moveu em direção ao lado direito até o nível de equilíbrio. F é zero e a velocidade v é máxima. A energia fornecida aqui para o objeto é dada de acordo com a velocidade. Na figura e, a mola foi esticada até o nível máximo e o objeto foi movido para a extrema direita. Agora, novamente, a velocidade aqui é igual a zero e a direção da força novamente está para o lado esquerdo, mostrada aqui como F é igual a zero. A energia fornecida aqui para o objeto é dada de acordo com a velocidade.
    Figura\(\PageIndex{1}\): A transformação da energia em movimento harmônico simples é ilustrada para um objeto preso a uma mola em uma superfície sem atrito.

    O princípio de conservação de energia pode ser usado para derivar uma expressão para velocidade\(v\). Se iniciarmos nosso movimento harmônico simples com velocidade zero e deslocamento máximo (\(x = X\)), então a energia total será

    \[\dfrac{1}{2}kX^2.\]

    Essa energia total é constante e é deslocada para frente e para trás entre a energia cinética e a energia potencial, na maioria das vezes sendo compartilhada por cada um. A conservação de energia para este sistema em forma de equação é assim:

    \[\dfrac{1}{2}mv^2 + \dfrac{1}{2}kx^2 = \dfrac{1}{2}kX^2.\]

    Resolvendo essa equação para\(v\) obter resultados:

    \[v = \pm \sqrt{\dfrac{k}{m}(X^2 - x^2)}.\]

    Manipular essa expressão algebricamente dá:

    \[v = \pm\sqrt{\dfrac{k}{m}}X\sqrt{1 - \dfrac{x^2}{X^2}}\]

    e assim

    \[v = \pm v_{max} \sqrt{1 - \dfrac{x^2}{X^2}},\]

    onde

    \[v_{max} = \sqrt{\dfrac{k}{m}}X.\]

    A partir dessa expressão, vemos que a velocidade é máxima (\(v_{max}\)) em\(x = 0\), conforme declarado anteriormente em\(v(t) = - v_{max} \, sin \, \frac{2\pi t}{T}\). Observe que a velocidade máxima depende de três fatores. A velocidade máxima é diretamente proporcional à amplitude. Como você pode imaginar, quanto maior o deslocamento máximo, maior a velocidade máxima. A velocidade máxima também é maior para sistemas mais rígidos, pois eles exercem maior força para o mesmo deslocamento. Essa observação é vista na expressão porque\(v_{max}\) é proporcional à raiz quadrada da constante de força.\(k\) Finalmente, a velocidade máxima é menor para objetos que têm massas maiores, porque a velocidade máxima é inversamente proporcional à raiz quadrada de\(m\). Por uma determinada força, objetos que têm grandes massas aceleram mais lentamente.

    Um cálculo semelhante para o pêndulo simples produz um resultado semelhante, a saber:

    \[\omega_{max} = \sqrt{\dfrac{g}{L}}\theta_{max}.\]

    Exemplo\(\PageIndex{1}\): Determine the Maximum Speed of an Oscillating System: A Bumpy Road

    Suponha que um carro tenha 900 kg e tenha um sistema de suspensão com força constante\(k = 6.53 \times 10^4 \, N/m\). O carro bate em uma colisão e salta com uma amplitude de 0,100 m. Qual é sua velocidade vertical máxima se você assumir que nenhum amortecimento ocorre?

    Estratégia

    Podemos usar a expressão for\(v_{max}\) dada em\(v_{max} = \sqrt{\frac{k}{m}}X\) para determinar a velocidade vertical máxima. As variáveis\(m\) e\(k\) são dadas na declaração do problema, e o deslocamento máximo\(X\) é de 0,100 m.

    Solução

    1. Identifique o conhecido.
    2. Substitua valores conhecidos em\(v_{max} = \sqrt{\frac{k}{m}}X\). \[v_{max} = \sqrt{\dfrac{6.53 \times 10^4 \, N/m}{900 \, kg}}(0.100 \, m).\]
    3. Calcule para encontrar\(v_{max} = 0.852 \, m/s\).

    Discussão

    Essa resposta parece razoável para um carro pulando. Existem outras maneiras de usar a conservação de energia para encontrar\(v_{max}\). Poderíamos usá-lo diretamente, como foi feito no exemplo apresentado em Hooke's Law: Stress and Strain Revisited.

    O pequeno deslocamento vertical\(y\) de um pêndulo simples oscilante, a partir de sua posição de equilíbrio, é dado como

    \[y(t) = a \, sin \, \omega t,\]

    onde\(a\) está a amplitude,\(\omega\) é a velocidade angular e\(t\) é o tempo gasto. Substituindo\(\omega = \frac{2\pi}{T},\), temos

    \[y(t) = a \, sin \left(\dfrac{2\pi t}{T} \right).\]

    Assim, o deslocamento do pêndulo é uma função do tempo, conforme mostrado acima.

    Além disso, a velocidade do pêndulo é dada por

    \[v(t) = \dfrac{2a\pi}{T} \, cos \left(\dfrac{2\pi t}{T}\right),\]

    então o movimento do pêndulo é uma função do tempo.

    Exercício\(\PageIndex{1}\)

    Por que dói mais se sua mão é quebrada com uma régua do que com uma mola solta, mesmo que o deslocamento de cada sistema seja igual?

    Solução

    A régua é um sistema mais rígido, que carrega maior força com a mesma quantidade de deslocamento. A régua encaixa sua mão com mais força, o que dói mais.

    Exercício\(\PageIndex{2}\):Check Your Understanding

    Você está observando um oscilador harmônico simples. Identifique uma forma de diminuir a velocidade máxima do sistema.

    Solução

    Você pode aumentar a massa do objeto que está oscilando.

    Resumo

    • A energia no oscilador harmônico simples é compartilhada entre a energia potencial elástica e a energia cinética, com o total sendo constante:\[\dfrac{1}{2}mv^2 + \dfrac{1}{2}kx^2 = constant. \nonumber\]
    • A velocidade máxima depende de três fatores: é diretamente proporcional à amplitude, é maior para sistemas mais rígidos e menor para objetos com massas maiores:\[v_{max} = \sqrt{\dfrac{k}{m}}X. \nonumber\]