16.4: O pêndulo simples

Objetivos de

Ao final desta seção, você poderá:

• Meça a aceleração devido à gravidade.

Figura\(\PageIndex{1}\): Um pêndulo simples tem uma saliência de pequeno diâmetro e uma corda que tem uma massa muito pequena, mas é forte o suficiente para não se esticar sensivelmente. O deslocamento linear do equilíbrio é\(s\) o comprimento do arco. Também são mostradas as forças no bob, que resultam em uma força líquida de -\(mg \, sin \, \theta \) em direção à posição de equilíbrio - ou seja, uma força restauradora.

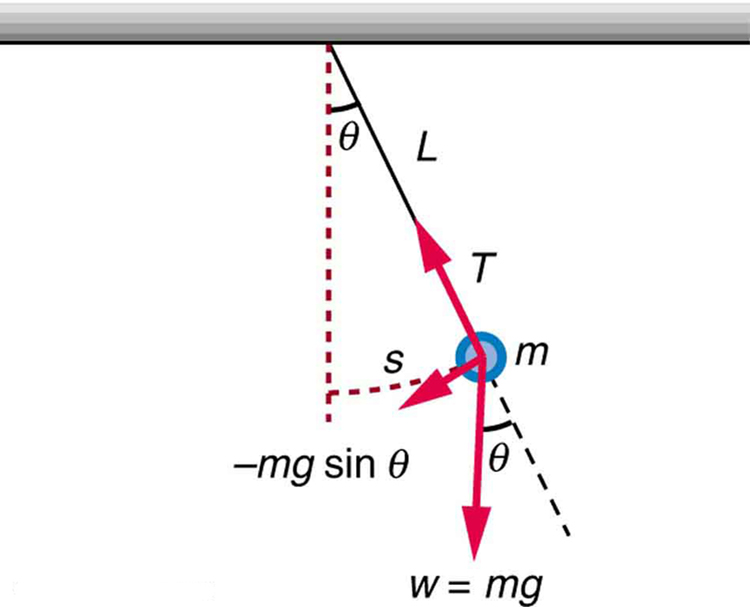
Os pêndulos são de uso comum. Alguns têm usos cruciais, como em relógios; alguns são para se divertir, como o balanço de uma criança; e alguns estão lá, como a chumbada em uma linha de pesca. Para pequenos deslocamentos, um pêndulo é um oscilador harmônico simples. Um pêndulo simples é definido para ter um objeto que tem uma massa pequena, também conhecido como pêndulo, que é suspenso por um fio leve ou corda, como mostrado na Figura\(\PageIndex{1}\). Explorando um pouco mais o pêndulo simples, podemos descobrir as condições sob as quais ele executa movimentos harmônicos simples e podemos derivar uma expressão interessante para seu período.

Começamos definindo o deslocamento como sendo o comprimento do arco\(s\). Vemos na Figura\(\PageIndex{1}\) que a força líquida no bob é tangente ao arco e é igual\(mg \, sin \, \theta\). (O peso\(mg\) tem componentes\(mg \, cos \, \theta\) ao longo da corda e\(mg \, sin \, \theta\) tangente ao arco.) A tensão na corda cancela exatamente o componente\(mg \, cos \theta\) paralelo à corda. Isso deixa uma força de restauração líquida de volta à posição de equilíbrio em\(\theta = 0\).

Agora, se pudermos mostrar que a força de restauração é diretamente proporcional ao deslocamento, então temos um oscilador harmônico simples. Ao tentar determinar se temos um oscilador harmônico simples, devemos observar que, para ângulos pequenos (menores que cerca de\(15^o\)),\(sin \, \theta \approx \theta \, (sin \, \theta\) e\(\theta\) diferem em cerca de 1% ou menos em ângulos menores). Assim, para ângulos menores que cerca de\(15^o\), a força de restauração\(F\) é\[F \approx -mg\theta.\] O deslocamento\(s\) é diretamente proporcional\(\theta\) a. Quando\(\theta\) é expresso em radianos, o comprimento do arco em um círculo está relacionado ao seu raio (\(L\)neste caso) por:

\[s = L\theta,\]

para que

\[\theta = \dfrac{s}{L}.\]

Para ângulos pequenos, então, a expressão para a força restauradora é:

\[F \approx -\dfrac{mg}{L}s.\]

Essa expressão tem o formato:

\[F = -kx,\]

onde a constante de força é dada por\(k = mg/L\) e o deslocamento é dado por\(x = s\). Para ângulos menores do que aproximadamente,\(15^o\) a força de restauração é diretamente proporcional ao deslocamento, e o pêndulo simples é um oscilador harmônico simples.

Usando essa equação, podemos encontrar o período de um pêndulo para amplitudes menores que cerca de\(15^o\). Para o pêndulo simples:

\[T = 2\pi \sqrt{\dfrac{m}{k}} = 2\pi \sqrt{\dfrac{m}{mg/L}}.\]

pelo período de um pêndulo simples. Esse resultado é interessante por causa de sua simplicidade. As únicas coisas que afetam o período de um pêndulo simples são seu comprimento e a aceleração devido à gravidade. O período é completamente independente de outros fatores, como a massa. Como acontece com osciladores harmônicos simples, o período\(T\) de um pêndulo é quase independente da amplitude, especialmente se\(\theta\) for menor que cerca de\(15^o\). Até mesmo relógios de pêndulo simples podem ser ajustados com precisão e precisão.

Observe a dependência\(T\) de\(g\). Se o comprimento de um pêndulo for conhecido com precisão, ele pode realmente ser usado para medir a aceleração devido à gravidade. Considere o exemplo a seguir.

Exemplo\(\PageIndex{1}\): Measuring Acceleration due to Gravity: The Period of a Pendulum

Qual é a aceleração devido à gravidade em uma região onde um pêndulo simples com 75.000 cm de comprimento tem um período de 1.7357 s?

Estratégia

Somos solicitados a determinar\(g\) o período\(T\) e o comprimento\(L\) de um pêndulo. Podemos resolver\(T = 2\pi \sqrt{\frac{L}{g}}\)\(g\), assumindo apenas que o ângulo de deflexão seja menor que\(15^o\).

Solução

1. Faça um quadrado\(T = 2\pi \sqrt{\frac{L}{g}}\) e resolva para\(g\):\[g = 4\pi^2 \dfrac{L}{T^2}.\]
2. Substitua valores conhecidos na nova equação:\[g = 4\pi^2 \dfrac{0.75000 \, m}{(1.7357 \, s)^2}.\]
3. Calcule para encontrar\(g\):\[g = 9.8281 \, m/s^2.\]

Discussão

Esse método de determinação\(g\) pode ser muito preciso. É por isso que a duração e o período são atribuídos a cinco dígitos neste exemplo. Para que a precisão da aproximação\(sin \, \theta \approx \theta\) seja melhor do que a precisão do comprimento e do período do pêndulo, o ângulo máximo de deslocamento deve ser mantido abaixo de aproximadamente\(0.5^o\).

FAZENDO CONEXÕES DE CARREIRA

O conhecimento\(g\) pode ser importante na exploração geológica; por exemplo, um mapa\(g\) de grandes regiões geográficas auxilia no estudo das placas tectônicas e ajuda na busca por campos de petróleo e grandes depósitos minerais.

EXPERIÊNCIA PARA LEVAR PARA CASA: DETERMINANDO\(g\)

Use um pêndulo simples para determinar a aceleração devido à gravidade\(g\) em seu próprio local. Corte um pedaço de barbante ou fio dental de forma que tenha cerca de 1 m de comprimento. Prenda um pequeno objeto de alta densidade na extremidade da corda (por exemplo, uma porca de metal ou uma chave de carro). Começando em um ângulo menor que\(10^o\), permita que o pêndulo gire e meça o período do pêndulo por 10 oscilações usando um cronômetro. Calcule\(g\). Quão precisa é essa medição? Como isso pode ser melhorado?

Exercício\(\PageIndex{1}\)

Um engenheiro constrói dois pêndulos simples. Ambos são suspensos por pequenos fios presos ao teto de uma sala. Cada pêndulo paira 2 cm acima do chão. O pêndulo 1 tem um bob com uma massa de\(10 \, kg\). O pêndulo 2 tem um bob com uma massa de\(100 \, kg\). Descreva como o movimento do pêndulo será diferente se ambas as bobinas forem deslocadas\(12^o\).

Resposta

O movimento do pêndulo não será diferente porque a massa do pêndulo não tem efeito sobre o movimento de um pêndulo simples. Os pêndulos são afetados apenas pelo período (que está relacionado ao comprimento do pêndulo) e pela aceleração devida à gravidade.

EXPLORAÇÕES PHET: PENDELUM LAB

Brinque com um ou dois pêndulos e descubra como o período de um pêndulo simples depende do comprimento da corda, da massa do pêndulo e da amplitude do balanço. É fácil medir o período usando o cronômetro photogate. Você pode variar o atrito e a força da gravidade. Use o pêndulo para encontrar o valor de\(g\) no planeta X. Observe o comportamento anarmônico em grande amplitude.

Figura\(\PageIndex{2}\): Pendulum Lab

Glossário

pêndulo simples

um objeto com uma pequena massa suspensa por um fio ou corda leve